基于LSQR与系统距离聚类算法的专变用户非介入式负荷辨识

易姝慧，郭俊岑，刁新平，刁赢龙

(中国电力科学研究院，武汉430070)

0 引 言

随着智能电力负荷概念的提出[1]，智能用电用户数量越来越庞大、负荷类型越来越复杂、用电服务越来越精细。在此发展趋势和技术需求下，研究面向智能用电的负荷监测关键技术，能够提高智能用电负荷数据采集与传输效率，提升负荷设备的监测识别准确率，促进负荷监测的深度挖掘与应用，为实现灵活互动的智能用电提供技术支撑。

目前，负荷监测方法主要有介入式负荷监测(Intrusive Load Monitoring，ILM)和非介入式负荷监测(Non-Intrusive Load Monitoring，NILM)两种[2]。由于NILM具有成本低廉、通信简单、便于维护和推广等优点，已成为可替代ILM的主流监测方法，可以对用户侧负荷进行实时监测和分析，引导用户主动节能。基于NILM的负荷特征提取[3]、负荷辨识[4]、负荷预测[5]等课题，是需求侧负荷监测的研究热点，国内外已有大量学者展开了深入研究，而目前的研究方向主要集中在居民用户。文献[6]针对家庭负荷，提出一种新的概率图形建模方法，利用多变量时间序列数据进行能量分解。文献[7]建立负荷稳态波形模版库，并提出了一种利用动态时间弯曲算法计算与模版库波形的距离来识别家用负荷的辨识方法。文献[8-9]基于V-I轨迹的设备负载特征针对高精度住宅负荷分解与预测模型进行研究。文献[10]提出了一种高频采集模式下的非侵入式负荷在线监测方法。以上研究成果主要针对家用电器建立负荷特征库，完成负荷分解辨识工作。

目前一些研究成果针对负荷稳态过程将隐马尔可夫模型、人工神经网络等深度学习智能算法应用于稳态过程负荷辨识。文献[11]采用4个稳态负载特征作为模型的观测向量，通过多参数隐马尔可夫模型学习和多次迭代求解，完成对负荷的最终辨识。文献[12-13]提出基于神经网络算法的深度学习模型的负荷辨识方法在非介入式负荷监测用电行为分析方面的有效性与准确性。文献[14]采用深度可分离卷积代替传统卷积并提出一种基于联邦学习的网络模型实施方案，以云边协同的方式对模型进行训练。文献[15]将图像信号处理方法用于电力系统进行负荷辨识。文献[16]提出基于时间分区和V型粒子群优化的非侵入式负荷分解算法。

另一部分研究成果是采用暂态负荷特征进行负荷辨识，进一步监测负荷的投切状态。文献[17]基于负荷功率的暂态特征进行分析，提出通过比较各个负荷特征数据的贴近度来进行负荷辨识的方法。文献[18]对时域暂态电流进行S变换处理而获取频域负荷特征，改进0-1多维背包算法来实现负荷监测辨识。文献[19]电器的功率数据进行状态提取，并利用电器运行的时间信息提取每个状态的时间概率分布，在负荷分解阶段利用时间概率最大似然估计分解结果。文献[20]针对工业电力负荷研究了一种基于事件波形解析的辨识方法，为了适应不同用户生产门类及流水工艺的差异，将事件解析下沉至用户边缘。文献[21]通过分析工业负荷运行特征提出基于滑动双边窗的事件探测算法。文献[22]对目标电器的不同功率状态进行编码,用循环卷积神经网络提取输入负荷总功率的空间时间特征。

上述研究成果一方面主要针对家用负荷，实验数据多采用开放REDD数据集[23]进行测试，对专变用户的工业负荷分解辨识研究较少，缺乏工业负荷数据；另一方面是单一地针对稳态过程或暂态过程进行负荷特征提取与负荷辨识，缺乏稳态与暂态结合的整体负荷特征空间构建与负荷辨识过程。因此，提出一种针对专变用户工业负荷稳态过程与暂态过程相结合的负荷辨识方法，提取电流有效值、有功功率、无功功率等构建负荷稳态特征空间，利用LSQR算法进行稳态过程负荷分解；选取电流有效值、有功功率均值、无功功率均值、持续时间、电流有效值最大值等描述暂态发生前、中、后三个阶段的特征量，构建负荷暂态特征空间，结合系统距离聚类算法将专变用户工业负荷暂态事件进行分类，进一步辨识出哪一种或者哪一类负荷发生投切动作。

1 专变用户用电特征分析

专变用户特征分析是负荷分解辨识的基础，目前专变用户类型多样，不同类型的专变用户特征具有一定的差异。按照电价进行分类，将专变用户分为商业混合用电、办公、农用以及民用专变用户、非普工业专变用户以及大工业专变用户。专变用户的电能需求其本质是一个随时间波动的数值序列，对这个时间序列进行趋势分析和建模，就能分析出其内在的规律特点[24]。选取某混凝土厂设备侧监测对象，选用DL850型号示波记录仪以10 kHz采样频率采集了设备侧搅拌器、水泥螺旋、污水泵、除尘器等常用负荷类型的电流录波信息。由图1可见，专变用户设备侧负荷用电总体具备以下特征：

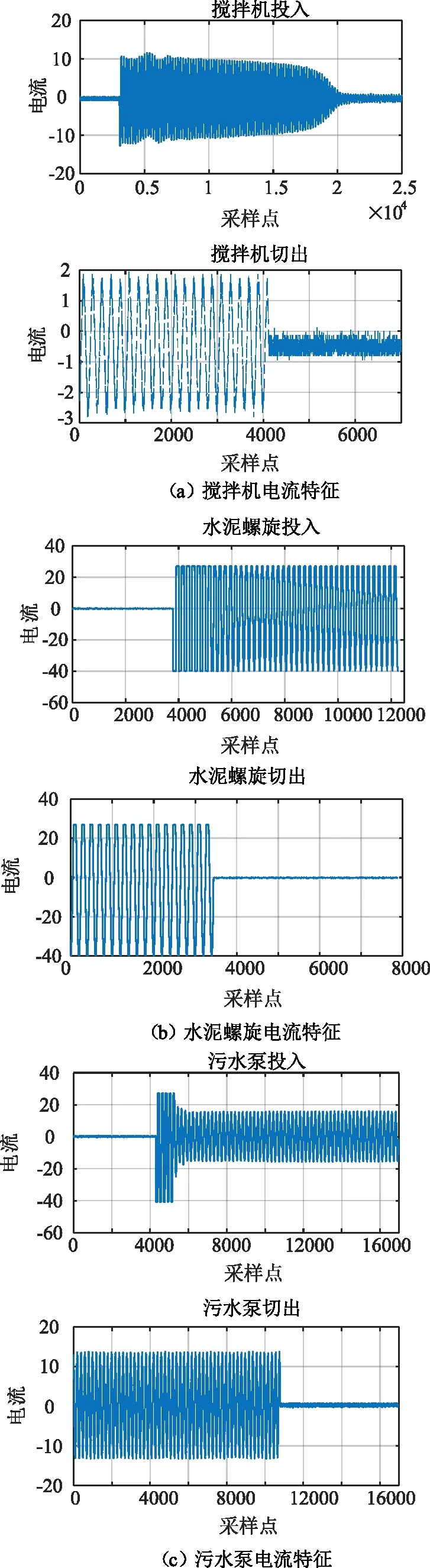
图1 常用负荷类型电流特征

(1)负荷电流随时间表现出了明显的波动特点；

(2)负荷投入切出时会引起瞬时电流较明显的变化；

(3)负荷投入切出后电流波形趋于稳定。

因此，专变用户经过负荷投入或负荷切出事件，会经历暂态前、中、后三个阶段，其中暂态前阶段指负荷投入或切出前原始的稳态，暂态后阶段指负荷投入或切出后另一种稳定状态，而暂态过程中电流、功率等用电特征会产生急剧变化。因此针对专变用户负荷辨识，有必要分别提取稳态过程特征与暂态过程特征。

1.1 专变用户负荷稳态特征提取

针对负荷稳态过程，一般选择有功、无功功率作为特征指标进行量测和处理，其公式如下：

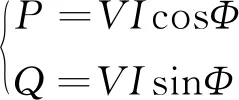
(1)

式中P、Q分别为有功功率、无功功率；V、I分别为电压、电流有效值；Φ为电压电流相位差;cosΦ为功率因数。

观察图1可知，专变用户负荷具有周期性，为了更全面地描述专变用户负荷特征，文中提取稳态过程的电流有效值也作为负荷特征指标，其公式如下：

(2)

式中N为一个周期内的采样点数；n为采样点序号；i(n)为每个采样点的瞬时电流值。

因此如表1所示，针对稳态过程提取有功功率、无功功率、电流有效值作为特征量，构建稳态过程特征空间。

表1 专变用户负荷稳态特征

1.2 专变用户负荷暂态特征提取

要实现对专变用户暂态过程的辨识，首先需要检测到暂态过程的发生，然后捕获到新旧两个稳态之间的暂态过程的波形，收集不同用电负荷的暂态特征样本。为了更全面地描述负荷暂态过程，提取暂态发生前、中、后三个阶段的特征量，针对非介入式负荷辨识，构建全面的暂态过程负荷特征空间。如表 2所示共计10种特征标签。

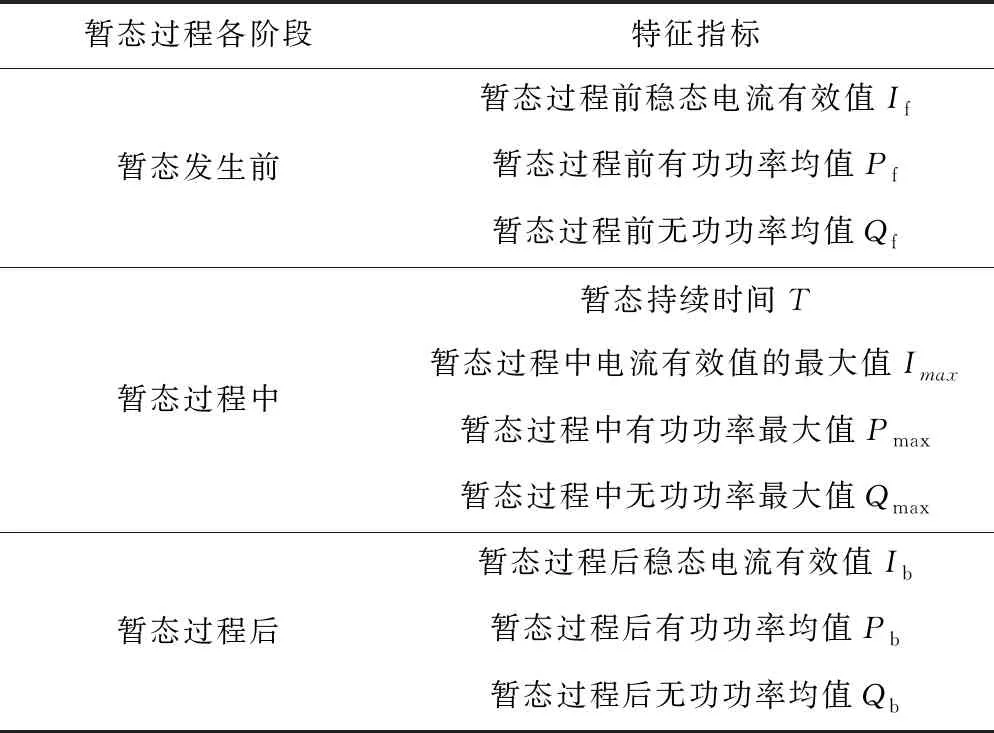
表2 专变用户负荷暂态特征

其中电流有效值可根据式(2)计算，有功功率、无功功率均值可根据稳态过程各个周期内有功功率值、无功功率值计算求得。以暂态过程前为例，计算如下：

(3)

式中T为暂态过程前的稳态波形周期数；Pn、Qn(n=1, 2, …,T)分别为第n个周期内的有功功率和无功功率。

2 基于稳态过程与暂态过程的负荷辨识方法

复杂工业环境下，存在数据采集困难、数据样本量较少等困难，因此采用LSQR与系统距离聚类两种分析算法进行负荷辨识，相较于深度学习算法需要大量样本进行训练学习，分析算法对数据样本需求量要求相对较低，基于有限样本的负荷辨识精度较高。

根据对专变用户用电特征的分析提取，将负荷投入后稳态过程的负荷分解，结合暂态过程的负荷投入切出辨识，从而基于稳态过程与暂态过程的负荷辨识方法，对非介入式专变用户负荷进行辨识。方法主要分为2个部分：稳态负荷分解过程可用最小二乘问题描述，采用LSQR算法对其进行优化求解；而暂态过程利用系统距离聚类算法将各种负荷投入切出对应的暂态事件进行分类，进而更精确地辨识出哪一种或者哪一类负荷发生投切动作。方法流程图如图2所示。

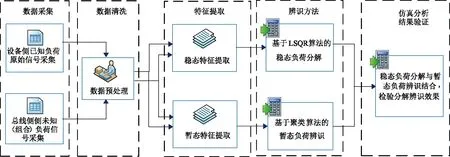
图2 基于稳态过程与暂态过程的负荷辨识方法流程图

2.1 专变用户样本数据清洗与处理

一方面，由于工业环境复杂，无论是设备侧还是总线侧采集波形时易出现粗大随机误差，需要剔除并修正无效数据。另一方面，为了客观全面地记录波形，通常采用高频率采集的方式采样电压和电流数据，但此方法同时也会造成数据量的急剧增长，对后续的数据处理效率造成一定程度的影响。此外，提取的专变用户负荷特征标签数据，一般不在统一量纲下，如果不做归一化处理，直接进行后续负荷辨识是没有意义的。综上原因，有必要对原始采样数据进行包括数据清洗、降采样、归一化等操作进行数据调整与处理。采用依拉达准则进行数据清洗，利用奈奎斯特法则进行降采样处理，最后利用最大最小归一化、Z-score归一化方法将相应特征标签数据进行去量纲操作。理论分别如下描述：

(1)依拉达准则

假设s1，s2，…，sn分别为原始采样数据，计算出算术平均值s及剩余误差vi=si-s(i=1，2，...，n)，并按贝塞尔公式算出标准误差σ，若某个测量值si的剩余误差vi，满足下式：

|vi|=|si-s|>3σ

(4)

则认为s是含有粗大误差值的坏值，应予以修正，文中用前后采样值的平均值来代替无效数据的方法进行修正。

(2)奈奎斯特采样定理

奈奎斯特采样定理规定了采样率和被采样信号频率之间的关系：采样率fs必须大于被采样信号最高频率分量的两倍，该频率通常被称为奈奎斯特频率fN，满足如下关系式：

fs>2fN

(5)

(3)最大最小归一化准则

最大最小归一化准则可将原始数据按线性化方法转换到[0 1]的范围。假设sij为第i种负荷的第j个用电特征的值，min(si)表示第i种负荷所有用电特征中的最小值；同理max(si)表示第i种负荷所有用电特征中的最大值，则有：

(6)

式中Z(sij)为变量sij标准化后的值。

(4)Z-score标准归一化准则

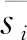
(7)

式中Z(sij)为变量sij标准化后的值。

2.2 基于LSQR算法的稳态过程负荷分解

(1)问题描述

基于NILM的稳态过程负荷分解原理，即给定一个已知的负荷特征数据库和某场景下组成元素未知的复合负载特征数据库，将复合负载信号分解为若干属于上述已知数据库的可识别负荷的加权组合，并求解各负荷的组成权重，即表示各负荷的使用状态。上述过程可以描述为以下数学问题：

(8)

上述稳态过程负荷分解问题其本质是求解如式(8)描述的线性最小二乘问题。一般负荷特征矩阵H不满足正定性，因此采用LSQR算法[25-26]，利用稀疏矩阵特性，近似迭代求解如式(8)所示负荷分解线性最小二乘问题。

如图3所示，LSQR算法求解包括两部分：第一步是进行Golub-Kahan迭代二对角化，以达到简化计算的目的；第二步是求解二对角化后的最小二乘问题。下面做详细分析。

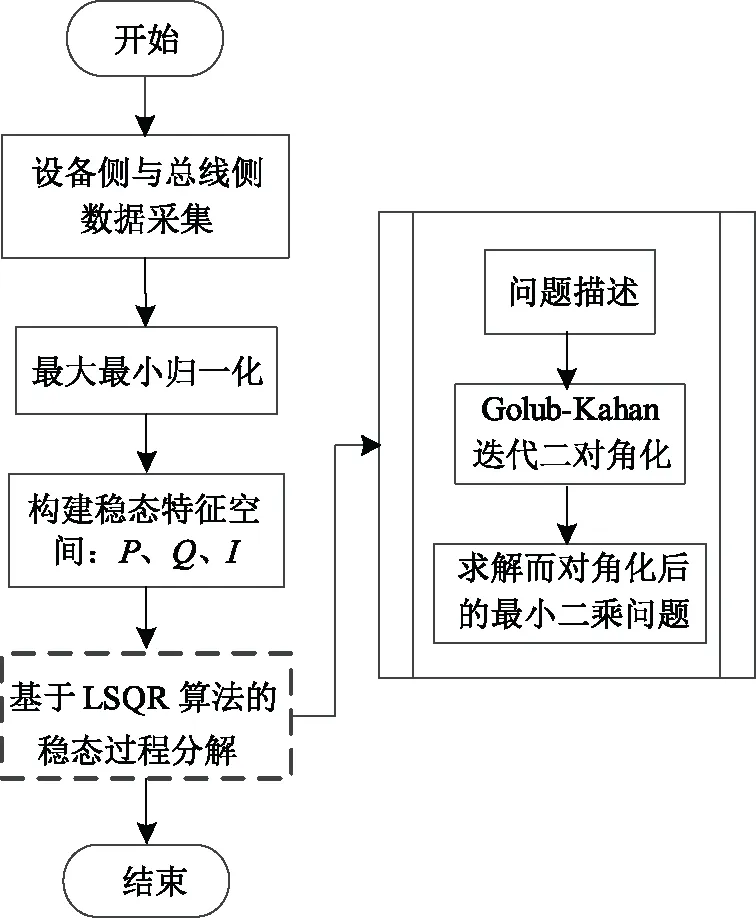
图3 基于LSQR算法的稳态过程负荷分解

(2)Golub-Kahan二对角化

基于Golub-Kahan二对角化方法，即通过奇异值分解方法对式(8)中负荷特征矩阵H进行二对角化稀疏变换，将H变换为双对角矩阵形式：

(9)

式中U=[u1,u2,…,uP]和V=[v1,v2,…,vP]均为酉矩阵，可通过迭代的方法计算求出，P为迭代次数。

令式(9)两边左乘U，有UUHHV=UB，得到：

(10)

因此，Hvk=αkuk+βk+1uk+1或βkukHvk-1-αk-1uk-1(k=1, 2,…,P)。

另一方面，对式(9)两边做Hermit变换得到VHHHUBH，如果两边左乘V，得到HHU=VBH=VBT，即：

(11)

因此，HHuk=βkvk-1+αkvk或αkvkHHuk-βkvk-1(β1=0,k=1,2,…,P)。

基于Golub-Kahan方法的二对角化可将负荷特征矩阵H变换为稀疏二对角矩阵B，从而降低求解最小二乘问题的计算复杂度，总结Golub-Kahan二对角化过程如下：

Step2：ForP=1,2,……

(12)

End

(3)最小二乘问题求解

基于P次迭代二对角化后，式(8)所描述的负荷分解线性最小二乘问题可转化为具有稀疏二对角矩阵B的最小二乘问题：

(13)

式中BP为(P+1)×P二对角矩阵，cP=VHx为稀疏二对角矩阵最小二乘问题的解，可根据式(13)利用QR分解求出。由于V为酉矩阵，基于cP可求出原负荷分解最小二乘问题的解，即：

(14)

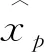
2.3 基于系统距离聚类算法的暂态过程负荷辨识

针对不同暂态负荷特征，采用基于系统距离聚类算法对未知暂态事件进行分类，从而判断未知的暂态过程所对应的负荷操作，从而实现暂态过程负荷辨识。根据表2所示负荷特征空间，该算法[27-28]主要流程如下：

Step 1：未知暂态事件出现时，提取其对应的负荷特征值，构造未知暂态事件特征向量Fnew=[T、If、Ib、Imax、Pf、Qf、Pb、Qb、Pmax、Qmax]，各分量均为Z-score归一化后的无量纲数值;

Step 2：假设有G种已知的专变用户负荷操作对应的暂态事件，将其负荷特征向量作为簇心，构造簇心集合C=[C1，C2，C3，…，CG]，分别计算Fnew到各个簇心的欧式距离得到距离集合D=[d1，d2，d3，…，dG];

Step 3：找到D中最小距离dmin，选择合适的阈值β，若dmin<β则Fnew属于dmin对应的簇心，否则以Fnew为新的簇心加入到集合C中;

Step 4：未知暂态出现时，重复Step1～Step3。

3 算例分析

3.1 评价指标

为了合理评价负荷分解的效果，选择最小归一化误差作为算法评价指标以表示负荷分解的精确度，定义如下：

(15)

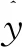
3.2 仿真算例

选择工业电力专变用户常用的15 kW排水泵、22 kW排水泵、搅拌机(电流变比60：1)、水泥螺旋4种负荷，总线侧电流变比为100:1，电压变比为1:1，选用DL850型号示波记录仪以10 kHz采样频率采集录波信号，由于三相电压、电流一致，所以仅针对其中一相进行数据预处理，进而分别在设备侧与总线侧对负荷分解辨识模型进行训练测试。

(1)数据预处理

采用依拉大法则剔除随机误差数据，得到相对平滑的波形数据。根据奈奎斯特定理，对10 kHz数据以1 kHz频率进行降采样处理，既降低系统对采样设备的要求，又可提高数据预处理的效率。降采样后的数据并不影响负荷特征提取，同时使数据量减少为原来的十分之一。

(2)稳态过程分解

根据表1提取稳态过程用电特征指标，构造负荷特征矩阵如表3所示。由于每种用电特征指标单位不统一，又由于负荷分解结果必须非负，因此选择最大最小归一化方法进行无量纲处理，根据式(6)处理后的特征矩阵如表4所示。

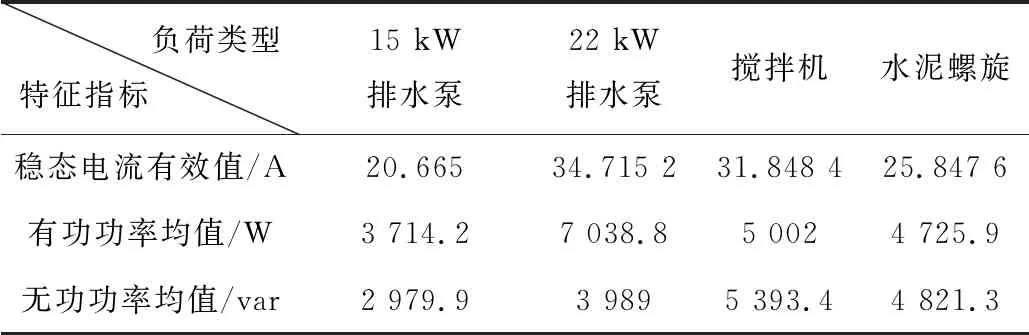
表3 负荷稳态特征矩阵表

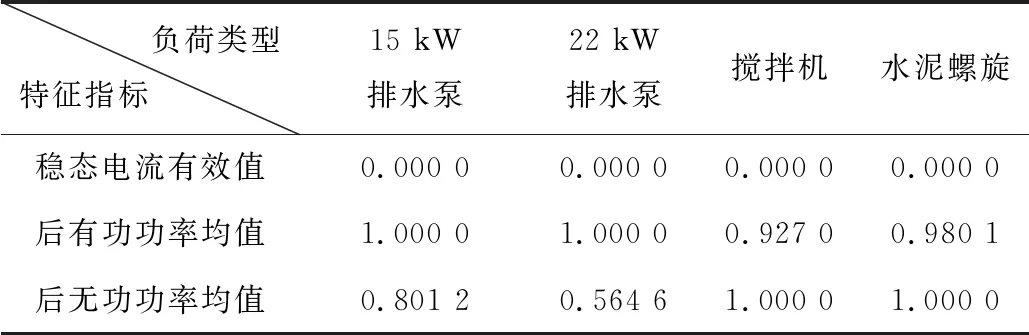
表4 负荷稳态特征归一化矩阵表

在总线侧采集4组未知负荷测试数据1、测试数据2、测试数据3、测试数据4，参照已知负荷类型的特征指标及提取方法，分别对每组未知负荷提取相应的用电特征，利用LSQR负荷分解算法结合表4所示的特征矩阵，分别将每组未知负荷分解为4种已知负荷的线性组合，完成稳态负荷分解。未知负荷分解为各已知负荷的组成权重，以及负荷分解结果与实际未知负荷测试数据的评估误差如表5所示，由表可知每次负荷分解的计算时间基本保持稳定。此外算法对负荷特征参数波动具有较强的抗干扰能力，以15 kW排水泵为例，其稳态电流有效值动态波动±5 A，由于采用了最大最小归一化方法，所有负荷特征参数为无量纲的相对值，屏蔽了某一参数动态变化对整体的影响，因此并不改变负荷稳态特征归一化矩阵。

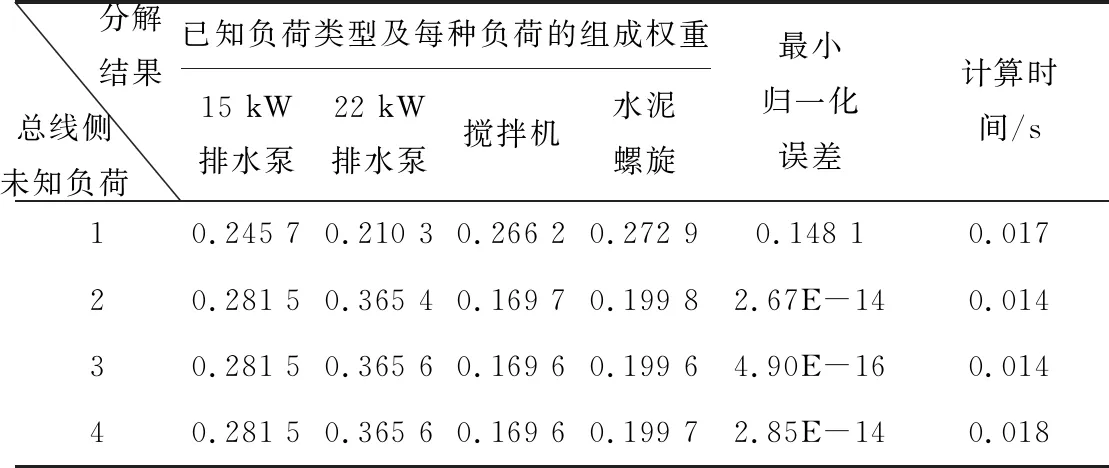
表5 稳态负荷分解结果

最后，为验证算法性能差异，以单样本为例，选取文献[29-30]中的负荷辨识算法，从误差率及计算时间与所提模型进行比较，结果如表6所示。所提算法相对其他新颖机器学习模型虽然在计算速度上不具备优势，但在误差率上具有明显优势。

表6 模型误差率及计算时间对比

(3)暂态过程辨识

选择与稳态负荷分解过程相同的四种常见专变用户负荷，每种负荷具有投入、切除两种暂态过程，构造了8个聚类簇心，覆盖算例中所有负荷投入切出的暂态事件。根据表2分别对每个簇心提取10种暂态过程负荷特征指标，并采用式(7)Z-score归一化方法去量纲处理。当总线侧出现未知暂态事件时，提取对应的特征指标并作相同归一化处理，采用系统距离聚类算法对未知事件进行分类合并，从而辨识出未知暂态事件所对应的具体负荷的投入切出操作。

经过聚类辨识，未知暂态时间与簇心事件拟合度基本一致，进一步验证了所提暂态过程负荷辨识方法的有效性。

4 结束语

针对工业电力系统专变用户提出了一种负荷分解辨识方法。针对负荷投入切出操作导致的暂态过程及负荷操作后的稳态过程，分别提取并构建用电特征空间。利用LSQR算法求解稳态过程负荷分解最小二乘问题，结合暂态过程聚类算法对暂态事件进行分类，进而达到辨识负荷投切操作的目的。仿真结果表明，所提方法能够有效地将专变用户负荷从未知负荷中分解出，误差率约为10-14，并且准确辨识出负荷投切操作。构建了一种专变用户负荷辨识通用处理流程，包括特征提取、数据预处理、稳态与暂态结合的负荷分解辨识等内容，可从未知总信号获取各种负荷详细的运行情况。提出的算法仿真是基于示波记录仪采集的专变用户负荷信号，后续仍需对动态实时信号采集与在线分析方面进行进一步研究。