功率自适应分配的孤岛直流微网控制策略研究
陈督好, 陈众
(长沙理工大学 电气与信息工程学院, 长沙 410114)
0 引 言
近年来, 为更好应对资源衰竭和环境污染等全球性问题, 发展和利用譬如太阳能、风能等分布式电源(Distributed Generation, DG)在国际上获得较大呼声, 微网作为一种整合了DG、储能系统和本地负荷的小型发电系统, 通过电力电子变换装置实现系统内各装置互联, 能够提高能源的利用效率, 根据断路器开合状态划分为并网和孤岛两种运行模式, 被认为是将DG接入电网最有效的途径之一[1]。相比于传统交流形式微网, 直流微网不用考虑频率稳定、无功、相位控制等因素, 系统简单、控制较为简便;此外, 由于分布式电源、储能、本地负载大部分为直流输出特性, 适合以直流形式接入网络, 避免中间额外变换过程, 成本得以降低, 效率进一步提高。因此, 直流微网具有很大的实际研究价值和经济意义[2-3]。
直流微网按运行模式分为并网运行和孤岛运行两种, 孤岛直流微网相对于并网状态更能体现控制策略的优越性 文章研究的对象为孤岛直流微电网, 孤岛直流微网缺乏交流大电网作支撑, 各环节均通过电力电子变换器接入公共母线, 公共母线电压的稳定和负荷功率的合理分配成为其稳定运行的两大必要条件[4]。集中控制及分散控制为目前负荷功率分配的两大主要方法。集中控制需要高速通信线和集中控制器为基础, 虽能实现控制目标, 但其过度依赖通信, 且容易出现单点故障;相对而言, 分散控制仅仅通过本地控制能够较好实现负荷分配, 与DG分布特性相符合, 对通信要求降低或者无需通信, 满足其即插即用需求, 目前学者研究比较热门的分散型控制方法是下垂控制方法[5-6]。
传统下垂控制未考虑线路阻抗不一致对其造成的影响, 实际直流微网运行中, 线路阻抗不同对负荷功率分配的影响不容忽略, 且其会产生电压降落, 从而公共母线进一步偏离电压给定值[7-8]。为削弱线路阻抗造成的影响, 科研人员在传统下垂控制的基础之上进行了一系列的改进措施, 大致可分为弱通信和无通信改进下垂控制两类方法。文献[9]引入中间参量电压变化率, 电流变化对电压产生的影响得以降低, 与传统下垂控制相比功率的分配精度得到相应提高, 但从其仿真和实验结果看出仍然存在误差。文献[10]根据负荷动态变化调整下垂系数, 无需通信可在重载情况下能够较好实现负荷功率分配, 但其在轻载情况下功率分配误差较大。文献[11]利用并网状态时大电网对直流母线电压的支撑获取线路阻抗信息, 将其以阻性虚拟阻抗引入下垂环节中消除线路阻抗影响, 但其不满足孤岛直流微网现实需要。文献[12-13]利用低速传输线, 额外加入二次控制, 即补充电压电流相应控制, 虽能较好实现功率分配, 但母线电压依然存在相应偏差量, 且单台DG通信压力相对偏大。文献[14]采集母线电压信息引入改进下垂控制, 虽能实现功率分配, 但其需要一直获取母线电压信息, 增大了通信线的信息传输压力。文献[15]设置相应通信拓扑, 信息在相邻DG间传输, 利用一致性算法实现控制目标, 在控制效果和通信需求间折中。综上, 无通讯分散控制不能同时较好地实现功率分配和公共母线的电压稳定目标, 弱通信分散控制虽能实现相应目标效果, 但由于对通信网络有需求, 当网络扩增时仍存相应通信压力, 系统的可靠性因此降低[17]。
为解决上述局限性问题, 文章提出了一种含负荷功率自适应分配能力的直流微网控制方法, 通过注入脉冲和检测实现对线路阻抗的主动辨识, 并将其以负虚拟阻抗引入传统下垂控制环节中用以抑制线路阻抗不一致产生的功率分配误差;同时由于其弥补了线路造成的压降, 较好地提升了公共母线的整体电压水平。所提控制策略不仅能实现负荷功率的准确分配, 且母线电压一直能够维持在较高的电压水平, 在无需通信网络的情形下, 依靠本地信息可实现直流微网控制目标, 具有热插拔功能。最后仿真和实验结果较好地验证了文章所提策略的可行性。
1 直流微网框架与P-V下垂控制
1.1 直流微网结构框架
图1为直流微网结构示意图, 其中主要包括源、网、荷、储四部分, 源即为DG, 通过单向变换器经线路阻抗接至直流母线;网即为交流大电网, 经断路器、变压器和双向变换器接入微网系统;荷为直流母线公共负荷;储为储能装置, 包含蓄电池为例的高能量密度型储能装置和以超级电容为例的高功率密度型储能设施, 经双向变换器接入公共母线电压环节, 用以平抑DG和负荷的功率波动。Ceq为直流母线系统等效电容, 当系统规模和容量增大时, 其数值不容忽略且随之增大, 用以稳定母线电压[16-17]。

图1 直流微网简要框架
1.2 传统P-V下垂控制
直流微网功率分配通常使用下垂控制方法, 类比与交流系统下垂方法,P-V下垂控制如下:
udci=uref+mi(Prefi-Pdci)
(1)
式中udci(i=1,2,…,n)为端口电压;Prefi为额定功率;Pdci为运行时输出功率;urefi为DG输出电压给定值;mi为P-V下垂控制对应比例系数, 若达到实际输出的功率按其输出能力分配负荷功率的理想状况, 下垂系数设为:
m1Pref1=m2Pref2=…=mnPrefn=M
(2)
如图2所示的是由两台带有P-V下垂DG构成的直流微网电路模型, 其中rL为本地负载等效阻抗, rlinei(i=1,2)为DG #i出线线路阻抗,uini(i=1,2)为变换器直流侧等效电源,upcc为公共点电压。

图2 双DG P-V下垂电路模型
根据图2所示电路结构可得DG发出实际功率与线路阻抗、DG变换器出口电压和公共母线电压之间的联系为:
(3)
联立式(1)~式(3)可得DG发出功率为:
(4)
在直流微网中, 理想情形各DG按其容量比例提供负荷功率, 故其提供的功率应满足:
(5)
当rline不容忽略, 定义两组DG负荷功率分配偏差如下:
(6)
将式(4)带入式(6)可得:
(7)
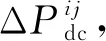
(8)
图3阐述了P-V下垂中因线路阻抗差异造成的负荷功率分配差异及公共直流母线电压偏差, 图中ΔPdc为功率分配差异, Δudci为造成的电压差异。
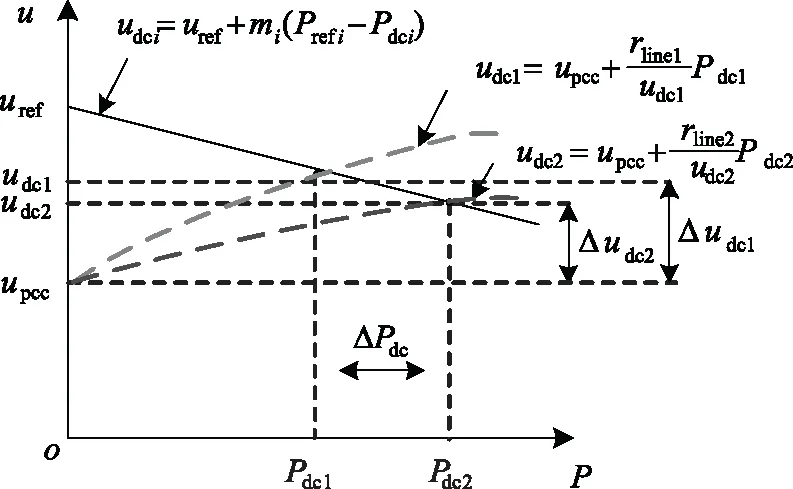
图3 P-V下垂局限性
综上, 当线路阻抗分布差异越突出, 传统下垂控制, 功率分配的误差会加剧, 同时公共直流母线电压跌落情况也会加剧, 对系统的稳定和运行产生不利影响, 因此需对传统P-V下垂控制进行优化处理。
2 孤岛直流微网自适应功率分配控制策略
针对线路阻抗分布差异对P-V下垂的影响, 提出基于虚拟阻抗的负荷功率自适应分配控制方法, 在不要求任何通信的基础下, 在实现功率按容量比例分配的同时, 能够有效地提升公共母线电压的水平。
图4为自适应负荷功率分配控制方法框架图。
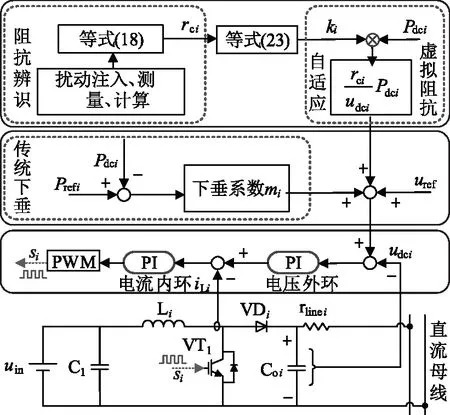
图4 控制策略框图
其包含两大要素:线路阻抗主动辨识和基于虚拟阻抗的负荷功率准确分配方法。线路阻抗主动辨识得到准确的阻抗参数;功率自适应分配方法将获得的阻抗信息构成虚拟阻抗成分加入传统控制当中, 达到功率自适应精确分配和提高公共母线电压水平的目的。
2.1 阻抗主动辨识方法
为完成各DG的负荷功率自适应精确分配, 要求得到相应线路的阻抗信息, 阻抗主动辨识包括以下三个步骤:注入相应微小扰动脉冲、对输出进行检测和利用检测结果计算阻抗信息, 下面将进行有效性分析。图5为DC-DC变换器基本控制框图[18], 其中虚线框表示的为内环控制。

图5 DC-DC变换器控制结构
控制结构设计时常常考虑内环响应速度远高于外环控制响应速度, 为简化分析, 将电流内环控制传递函数增益等效为1, 得到:
(9)
式中kp与ki为所采用的PI控制器当中对应的比例、积分增益。
图6是单独一台DG直流变换器简易模型, 依靠此模型进行各变量传递函数的阶跃响应分析。其中, Δu为注入的扰动脉冲电压。

图6 单DG变换器电路模型
由图6结合电路相关理论知识, 可得:
(10)
(11)
联立式(9)~式(11)可得:
(12)
(13)
式中:
(14)
用于响应分析的参数由表1所示, 根据上述所得传递函数带入相应数值可得各所需变量阶跃响应曲线图见图7。图7中, 当加入扰动脉冲后, DG变换器端口电压、电流相比upcc的上升速度要快的多, 甚至在0.2 ms内母线电压的波动可以忽略不计[19]。

表1 阶跃响应分析参数
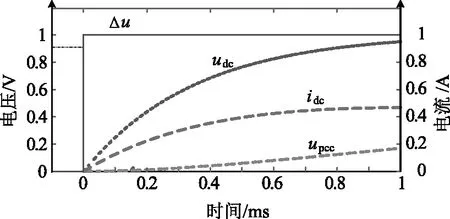
图7 注入扰动后的阶跃响应
运用等效电容此特性, 注入扰动脉冲后, 前后均对变换器的输出做相应检测, 检测时间间隔可适当根据实际情况选取, 由电路理论可得:
udc0-rlineidc0=upcc0
(15)
udc1-rlineidc1=upcc1
(16)
式中udci、idci和upcci(i=0,1)为前后两次测量输出电压, 输出电流及公共母线电压测量值。
联立式(15)和式(16)可得:
(17)
因此,根据实际情况选取适当检测时间间隔, 公共母线电压在此检测间隔期间无波动, 根据电路理论可得:
(18)
式中rc为线路阻抗辨识值。
2.2 基于虚拟阻抗的功率自适应分配策略
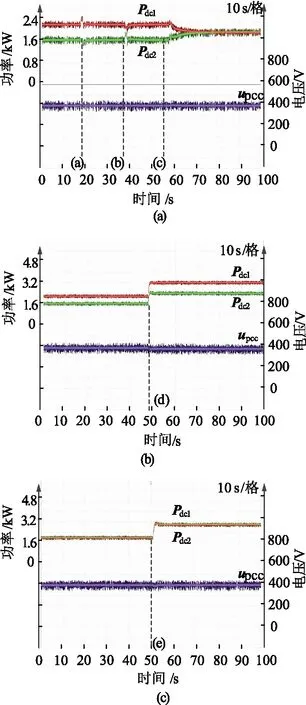
根据第1节, 各DG变换器出口线路阻抗分布差异越突出, 功率分配的误差会加剧, 同时公共直流母线电压跌落情况也会加剧。为解决上述问题, 提出了负荷功率自适应分配的控制策略, 图8为其原理示意图。为简化分析计算, 设置系统DG等额定功率和等下垂系数, 同时设计rline1 图8 功率自适应分配策略原理图 如图8所示, 由式(1)表示的L10(L20)是改进前P-V曲线, 由式(3)表示的R10、R20是此时DG变换器输出伏安关系曲线, 由式(3)变换得: (19) 因阻抗分布差异,R10和R20无法完全重合, 功率分配差异ΔPdc由此产生, 阻抗差异越大, 功率分配误差越明显。此时若将L10、L20变换到L11、L21, 且将R10、R20平移变换到R11、R21,L11、L21与R11、R21同样会产生交点, 此交点便为变换器工作稳态点, 当辨识值越精准,Pdc11与Pdc21越接近, 最终重合, 功率分配精度得到非常大的改善。 根据图8表述, 将式(1)改为: udci=uref+mi(Prefi-Pdci)+kiPdci (20) 式中ki为虚拟阻抗, 用以达到负荷功率的准确分配目标。联立式(20)与式(3)得: (21) 故DG功率分配相对偏差为: (22) 若达到理想状况, 即功率分配偏差为零, 推导出虚拟阻抗ki为: (23) 然而通过线路阻抗主动辨识已经测得相应DG出线线路阻抗, 故将其替换式(23)中的实际线路阻抗, 得到最终改进下垂控制表达式: (24) 为验证基于虚拟阻抗的功率自适应分配方法的可行性, 在Matlab/Simulink环境下建立了相应等额定功率的DG直流微网系统, 分别对功率分配的稳态和动态过程进行验证。表2为系统相关参数, 实验参数和仿真参数基本保持一致。图9为仿真模型结构示意图。 3.1.1 仿真算例1 利用2.1小节所提方法获得#1和#2阻抗信息分别为1.205 Ω和2.411 Ω, 阻抗主动辨识与阻抗实际值仅有细微差距, 并且可以通过改进辨识方法将此误差降低至更小, 此内容非文章主要内容, 不作详细阐述。如图10(a)所示, 6 s之前阻抗分布不一致产生负荷功率分配偏差过大, 6 s以后将获取的线路阻抗信息引入虚拟阻抗自适应功率分配控制中, 在1 s内时间即可实现负荷功率的准确分配, 可以看到功率曲线基本重合。如图10(b)所示, 当采用文章所提控制方法后, 由线路阻抗产生的电压降落得到了虚拟阻抗正向电压的弥补,upcc从起初未加控制的385 V上升至396 V, 提高了upcc的电压水平, 易于系统稳定。 3.1.2 仿真算例2 当功率需求波动时, 所提控制策略对功率分配的控制效果, 功率需求波动情况见表3, 相应仿真结果如图11所示。 表3 功率需求波动情况 在图11(a)中, 当功率发生波动时, 负荷需求由4 kW直到变化为8 kW, 在功率需求发生波动时, 两同容量的DG提供的功率曲线一直重合, 说明实现了负荷功率的精确分配, 从而提高了DG的能源利用效率, 减少了环流的产生。如图11(b)所示, 虚拟阻抗的存在抬升了公共直流母线电压, 使得母线电压能够维持稳定在较高的电压水平, 电压偏差较小。因此, 在负荷功率需求发生不断波动时, 功率分配依旧不受其影响, 在无需通信网络的情形下, 依靠本地信息可实现直流微网相应的控制目标。 图11 功率波动情形仿真结果 为验证理论分析和仿真结果正确性, 半实物仿真平台得以建立, 半实物系统主要包含上位机、DSP控制板、实时仿真器RT-LAB及示波器等, 实验平台实物图及实验结果波形分别由图12、图13所示。 图12 基于RT-LAB的硬件在环实验平台 图13 实验波形 如图13(a)所示, 同仿真分析, 在时间节点(a)与(b)注入脉冲扰动, 利用公共母线电容惯性特性获取线路阻抗信息, 在时间节点(c)将获取的阻抗信息引入基于虚拟阻抗功率自适应分配控制中, 引入控制后, 功率实现自适应准确分配, 同时公共直流母线电压有了近10 V的抬升。图13(b)为传统控制中负荷功率发生波动的实验结果图, 当负荷功率需求增加时, 功率分配的误差会加剧, 同时公共直流母线电压跌落情况也会加剧, 对直流微网的稳定与运行产生不利后果。图13(c)为文章所提控制策略在负荷功率需求波动情形下的实验结果图, 在负荷功率发生波动时可实现准确分配, 且母线电压一直能够维持在较高的电压水平, 在无需通信网络的情形下, 依靠本地信息可达到直流微网相应的目标效果。 为解决线路阻抗分布差异产生的负荷功率分配误差过大问题, 提出负荷功率自适应分配的控制方法, 利用母线等效电容的惯性特性辨识出各DG出口线路阻抗数值大小, 并将此信息构成虚拟阻抗成分加入传统控制当中, 达到功率自适应精确分配和提高公共母线电压水平的目的, 因无通信网络需求, 经济可靠且具有热插拔能力。最后, 基于文章提出的控制策略理论分析搭建了仿真及实验, 该策略的有效性得到了验证。
3 仿真及实验验证
3.1 仿真验证

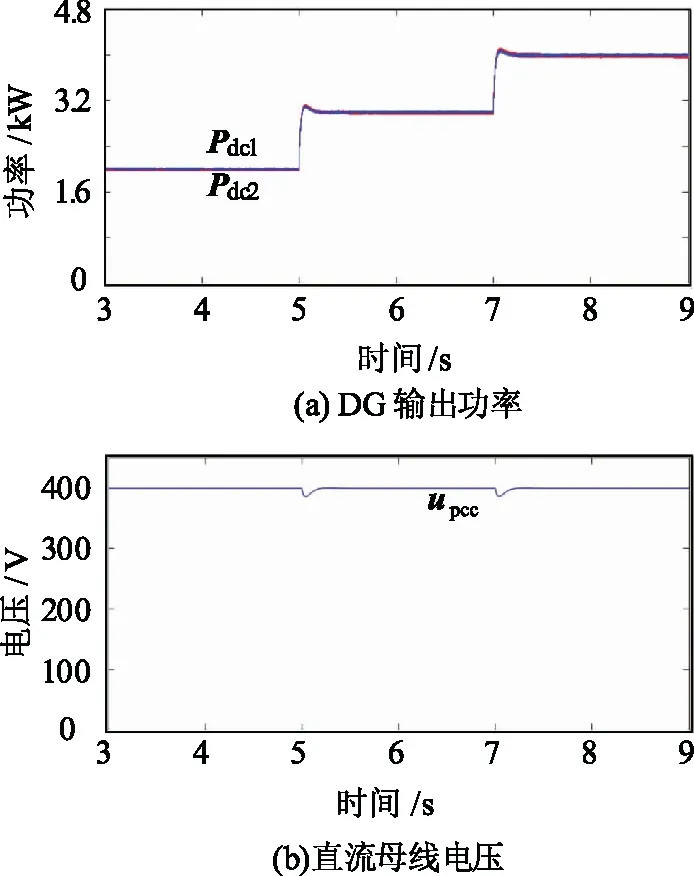
3.2 实验验证

4 结束语

