含中性点参数的三相变压器建模及其在潮流计算中的应用
姚玉斌,张悦,王爱芳
(大连海事大学 船舶电气工程学院,辽宁 大连 116026)
0 引 言
潮流计算是电力系统计算和分析的基础,相较于输电系统,配电系统的三相不平衡问题格外突出,无法直接采用单相潮流算法进行计算分析,因此对配电系统进行三相潮流计算是十分必要的[1-2]。变压器作为电力系统中最重要的电力设备之一,建立变压器的三相模型也是配电网潮流计算的基础工作[3-4]。
建立详细的变压器三相模型需注意以下因素,如考虑铜损和铁损、相位偏移问题,以及考虑中性点接地和不接地的变压器模型等[5-8]。变压器的实用模型可以由漏磁导纳矩阵和铁损等值回路两部分表示[6,9],铁损等值回路通常作为功率损耗合并至节点负荷或按经验公式计算[6],变压器建模时不再考虑励磁回路部分。漏磁导纳矩阵又称节点导纳矩阵,变压器三相建模的关键是得到变压器的三相节点导纳矩阵。
目前广泛采用对称分量法和关联矩阵法对变压器节点导纳矩阵进行推导,如文献[6, 10]采用基于序分量的对称分量法对变压器节点导纳矩阵进行推导,由文献[10]可知,对称分量法将变压器的电压(电流)相量分解为正、负、零序分量,有着计算速度快,占用内存较小等优点,但对称分量法不能在变压器参数不对称时使用。文献[11]采用基于相分量的关联矩阵法对变压器节点导纳矩阵进行推导,关联矩阵法可直接对变压器三相整体建模,较为直观,更适合应用于三相不对称的计算中。但对于绕组连接方式为中性点不接地的星形接线,由于其中性点电位不为零,变压器的绕组支路电压与节点电压的关系不再是关联矩阵,传统的关联矩阵法便不再适用。因此文献[12]提出了基于电气量变换矩阵法的三相变压器建模方法,解决了中性点不接地星形接线的变压器三相模型问题,但该方法的电压变换矩阵和电流变换矩阵不再互为转置,推导也较为复杂。目前中性点不接地星形接线的变压器模型中没有中性点电气量,进行潮流计算时,无法直接求出中性点电压。因此需要对中性点不接地星形接线的变压器三相模型进行研究,以推导其节点导纳矩阵。
文中分析了中性点不接地星形接线方式的变压器关联矩阵的特点,推导出了相同连接方式不同组别标号变压器关联矩阵的相互联系,提出了基于关联矩阵法的含中性点参数的变压器模型建立方法。通过文中方法可使关联矩阵法应用于中性点不接地的星形接线方式的变压器建模,建模过程也更加简洁,模型应用于潮流计算可以直接方便地求出变压器中性点电压。最后以IEEE-4节点标准测试系统为例对所述方法进行了验证。
1 不含中性点参数的变压器模型
图1为变压器的三相模型,三相变压器中存在一个公共铁芯,因而各绕组之间存在相互耦合。
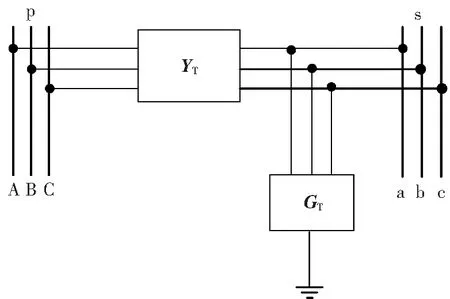
图1 三相变压器实用模型
通过变压器绕组之间的连接关系,可以用变压器原始导纳矩阵Yp来表示变压器三相绕组支路电压向量Ub和变压器绕组支路电流向量Ib之间的关系,如式(1):
Ib=YpUb
(1)
(2)
式中yt为三相变压器三相参数对称时每相绕组的短路导纳。
如图2所示为变压器非标准变比模型,将原边、副边绕组等效为两个理想变压器,α0是原边绕组的非标准变比,β0是副边绕组的非标准变比。

图2 变压器非标准变比模型
考虑非标准变比后,变压器的原始导纳矩阵可变为如下形式:
(3)
通过节点导纳矩阵YT可以表示变压器各端点的节点电压向量Un和节点电流向量In之间的关系:
In=YTUn
(4)
三相变压器绕组支路电压Ub和节点电压Un之间的关系为:
Ub=CUn
(5)
式中C为变压器的电压关联矩阵。
三相变压器绕组节点电流In和支路电流Ib之间的关系为:
In=GIb
(6)
式中G为变压器的电流关联矩阵。
如果变压器不存在中性点不接地星形连接方式,则G=CT。由原始导纳矩阵Yp、电压关联矩阵C可推导得出变压器节点导纳矩阵YT的表达式为:
YT=CTYpC
(7)
2 含中性点参数的变压器模型
变压器绕组连接方式为中性点不接地的星形接线时,由于中性点电位不为零,那么变压器的绕组支路电压与节点电压的关系就不能用关联矩阵表示,传统的关联矩阵法便不再适用。文献[12]提出了基于电气量变换矩阵法的三相变压器建模方法,解决了中性点不接地星形接线的变压器三相模型问题,但该方法的电压变换矩阵和电流变换矩阵不再互为转置,推导也较为复杂。目前中性点不接地变压器模型中没有中性点电气量,进行潮流计算时,无法直接求出中性点电压。因此需要对中性点不接地星形接线的变压器三相模型进行研究,以推导其节点导纳矩阵。
绕组连接方式为中性点不接地的星形接线时,如果变压器各端点的节点电压向量中包含中性点电压,各端点的节点电流向量中包含中性点电流,则式(7)对中性点不接地星形接线的变压器仍然适用。
变压器原副边相同连接方式下不同组别的变压器电压关联矩阵之间存在相互联系,可由一个基本电压关联矩阵与一个统一的转换矩阵运算推导出同一连接方式下不同组别变压器的电压关联矩阵,然后推导出变压器三相模型。
为分析方便起见,定义变压器原边绕组采用中性点接地星形连接、中性点不接地星形连接、三角形连接时,原边时钟分别为0、0、1;定义变压器副边时钟为变压器连接组别标号与原边时钟之和,如果所得到的和为12,则副边时钟为0。
变压器原边(副边)绕组采用时钟为0的中性点接地星形连接、时钟为0的中性点不接地星形连接、时钟为1的三角形连接时,对应的含中性点参数的原边(副边)电压关联矩阵分别为:
(8)
(9)
(10)
对所有接线类型的三相变压器,变压器的电压关联矩阵写成统一形式如下:
(11)
式中Cp为原边电压关联矩阵;Cs为副边电压关联矩阵;下标k表示副边时钟,k=0,1,…,11。
以Yd接线的变压器为例,讨论原副边相同接线方式下不同连接组别变压器的副边电压关联矩阵的关系,推导三相变压器的节点导纳矩阵。
Yd接线的变压器组别标号可以为1、3、5、7、9、11,Yd1接线的变压器等效电路图如图3所示。
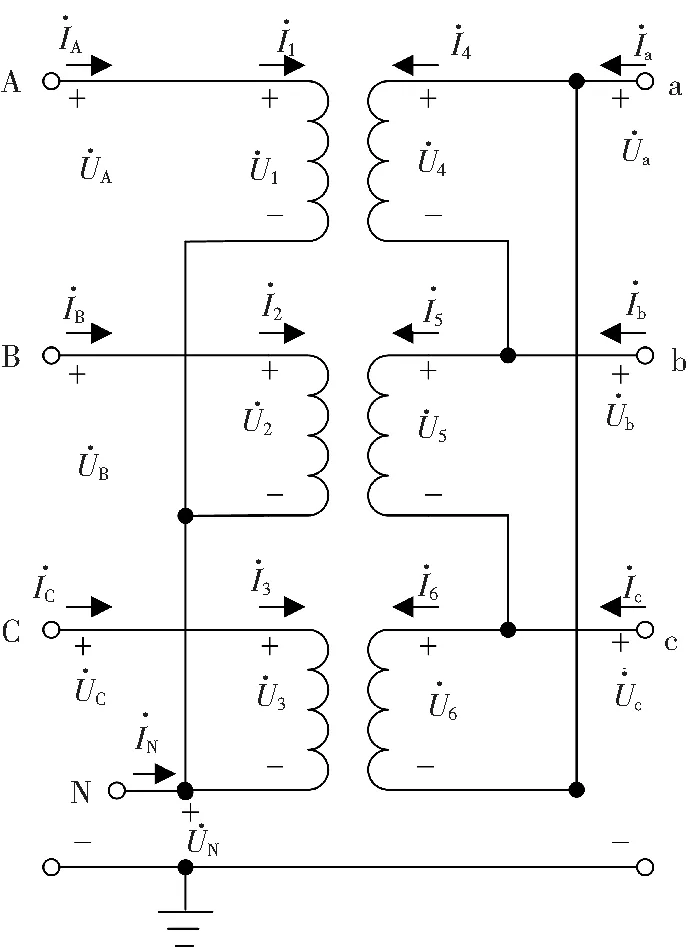
图3 Yd1变压器等效电路图
Yd1变压器绕组支路电压向量和绕组支路电流向量分别用Ub、Ib表示,同式(1)。Yd1变压器的节点电压向量和节点电流向量分别用Un、In表示,即:
式中UN为原边绕组的中性点电压;IN为原边绕组的中性点电流。
Yd接线的变压器原副边绕组的非标准变比与变压器相电压非标准变比之间的关系为:
(12)
将式(12)代入式(3)可以得到Yd接线的变压器原始导纳矩阵为:
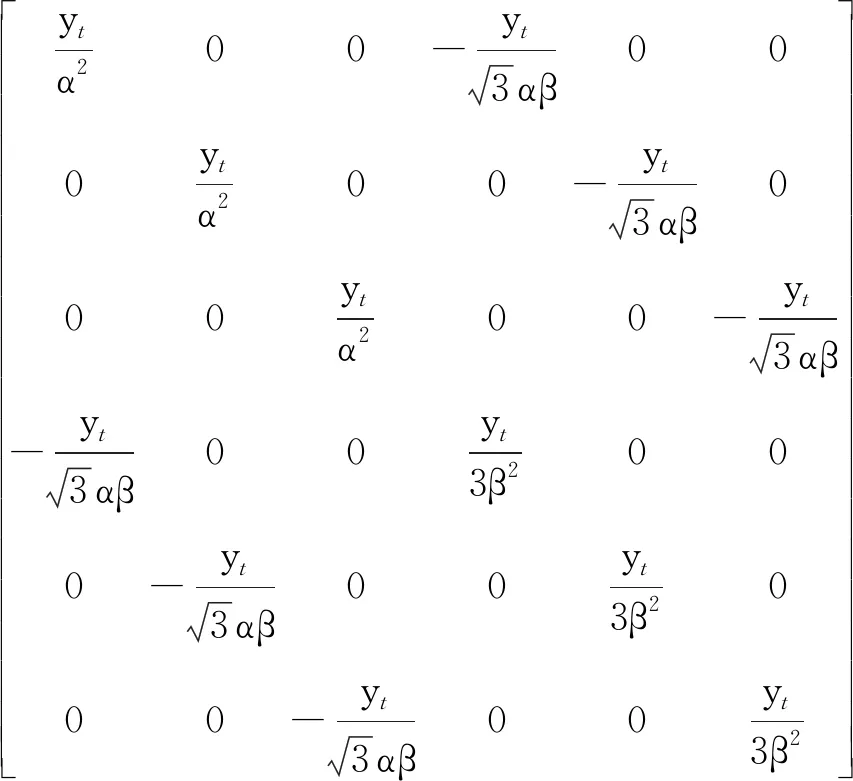
(13)
Yd1接线的变压器的支路电压与节点电压的关系为:
Ub=C1Un
(14)
(15)
根据变压器的原边、副边接线方式可以得到Yd1原边电压关联矩阵Cp和副边电压关联矩阵Cs1为:
(16)
(17)
变压器的原边绕组采用原边时钟为0的中性点不接地的星形接线,Cp=CY;变压器的副边绕组采用副边时钟为1的三角形接线,Cs1=CD。
观察变压器原副边绕组的接线,可以发现随着组别标号的变化,原边绕组不发生变化,只有副边绕组的相位关系发生变化,副边绕组的电压关联矩阵也随之改变。因此当组别标号变化时,只需对副边电压关联矩阵Cs的变化进行研究即可。图4为Yd接线的变压器不同组别的副边绕组接线方式。
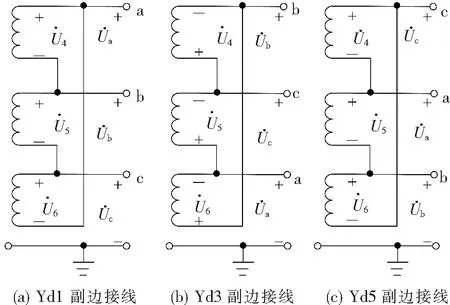
图4 Yd变压器副边绕组的接线
观察图4,Yd3变压器的副边绕组接线与Yd1变压器相比,有两个变化:(1)三相相序仍为正相序,但后移了一相,由a、b、c变为b、c、a;(2)极性相反。
式(1)可以通过转换矩阵E1实现:
(18)
式(2)可以通过转换矩阵E2实现:
(19)
结合式(18)和式(19),得到两个组别的变压器副边电压关联矩阵的转换矩阵为:
(20)
这样,得:
(21)
根据图4(b),可以看出Yd3接线的变压器的副边电压关联矩阵就是式(21),说明所推导的转换矩阵E是正确的。
Yd5变压器的副边绕组接线与Yd3变压器相比,也同样有两个变化:(1)三相相序仍为正相序,但后移了一相,由b、c、a变为c、a、b;(2)极性相反。这样也可以通过转换矩阵E由Cs3得到Cs5为:
(22)
同理,可以得到Yd7、Yd9、Yd11组别的变压器副边电压关联矩阵与Yd1副边电压关联矩阵的关系。
对其他接线方式的变压器也可以得到类似的结论,综合以上,各副边时钟对应的副边电压关联矩阵为:
Csk=CssEm(k=0,1,…,11)
(23)
式中变压器副边绕组为中性点接地星形连接时,Css=CYN;变压器副边绕组为中性点不接地星形连接时,Css=CY;变压器副边绕组为三角形连接时,Css=CD;指数m=0,1,…,5,为副边时钟k除以2之后的整数部分;转换矩阵E用来实现不同组别标号的副边电压关联矩阵之间的互相转换,副边绕组为中性点接地星形连接或三角形连接时,为:
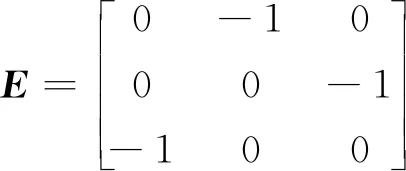
(24)
副边绕组为中性点不接地星形连接时,转换矩阵E为:
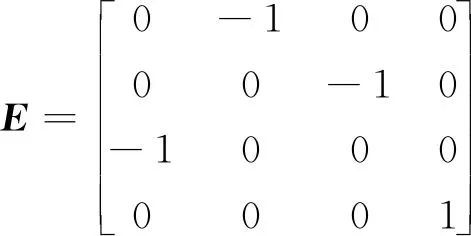
(25)
将得到的变压器副边电压关联矩阵Csk代入式(11)中求出电压关联矩阵Ck,再与式(13)中的原始导纳矩阵Yp一起代入式(7)中,便可以得到节点导纳矩阵YT。
为方便分析和观察,可以将节点导纳矩阵分块,如式(26)所示:
(26)
不同接线方式的三相变压器节点导纳矩阵如表1所示。

表1 三相变压器节点导纳矩阵

由表1可知,除含中性点不接地星形接线的变压器外,本文导出的三相变压器节点导纳矩阵与文献[6]所得到的节点导纳矩阵完全相同。与文献[6]相比,本文导出的含中性点参数的变压器的节点导纳矩阵中包含有中性点参数,使含中性点不接地星形接线的变压器三相模型更加直观。
3 变压器模型在潮流计算中的应用
以IEEE-4节点标准测试系统为例,采取电流偏差型直角坐标牛顿法进行潮流计算,验证提出的含中性点电气量的变压器三相模型的正确性。
IEEE-4节点系统接线图如图5所示,节点1为平衡节点,其线电压幅值为12.47 kV,A、B、C三相电压相角分别为0 °、-120 °、120 °。选择连接组别为Yd1的三相降压变压器,节点4接三相不对称负荷,A、B、C三相有功功率分别为1 275 kW、1 800 kW、2 375 kW,功率因数分别为0.85、0.9、0.95,设置收敛精度为0.000 1。
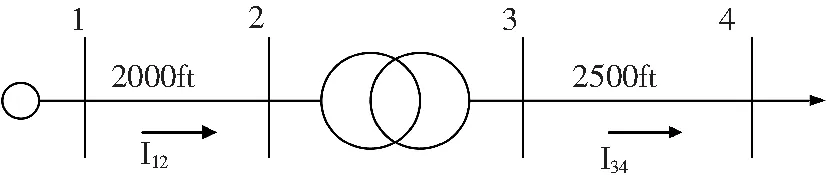
图5 IEEE-4节点系统
牛顿法在导纳矩阵对称性及稀疏性有着明显优势,因此在中低压配电网潮流计算中常采用牛顿法进行计算[13]。但由于潮流计算的雅可比矩阵奇异,会导致牛顿法收敛困难[14],故在各节点每相上加一个电纳值为10-6S的小电容,因电容值很小,不影响最终的计算精度。
为验证所使用方法的正确性,采用文献[15]中的“Ladder Iterative Technique”方法作为对比方法对相同算例进行了潮流计算。
采用文中方法和对比方法对算例进行潮流计算,得到的各节点电压如表2所示。
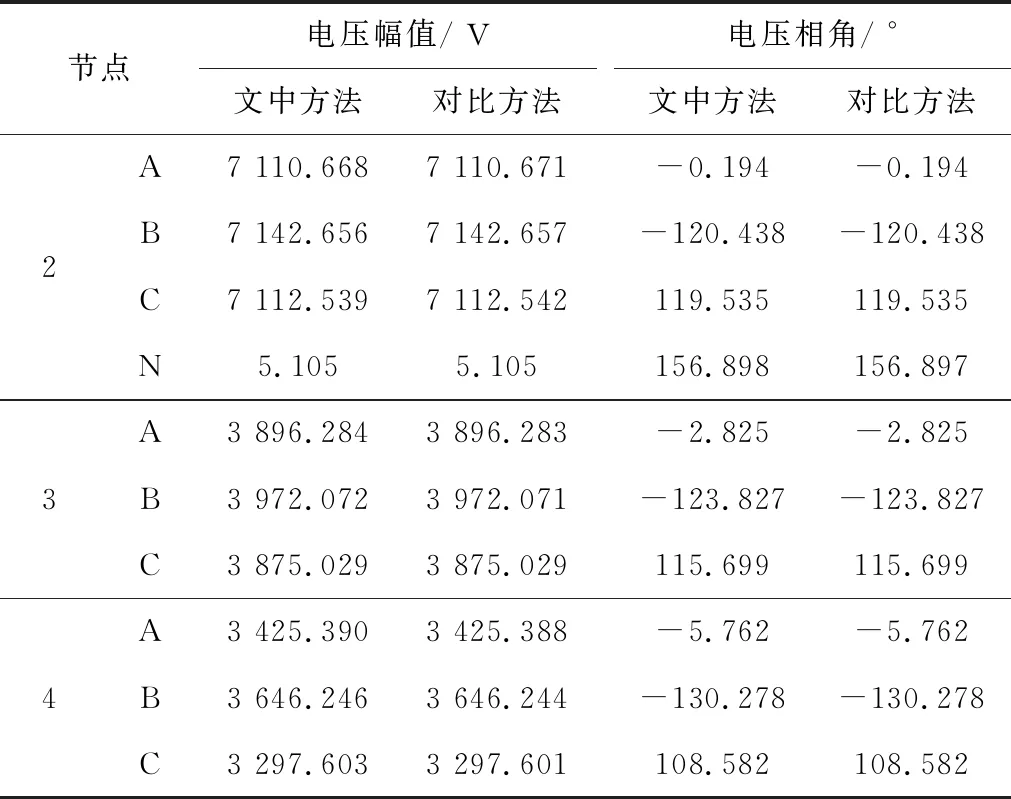
表2 不同方法潮流计算的节点电压
由表2和表3可知,计算结果保留三位小数时,采用文中方法和对比方法潮流计算得到的节点电压幅值计算结果相差很小,均在0.01 V以内,节点电压相角计算结果相差也很小,均在0.001°以内;支路电流幅值计算结果相差很小,均在0.01 A以内,支路电流相角计算结果相差也很小,均在0.001°以内。由此说明采用文中方法建立的变压器三相模型是正确且有效的。而且基于本论文模型的电流偏差型直角坐标牛顿法不仅可用于辐射形配电网,还可以用于环形配电网,比仅适合于辐射形配电网的“Ladder Iterative Technique”方法的适应面更广。
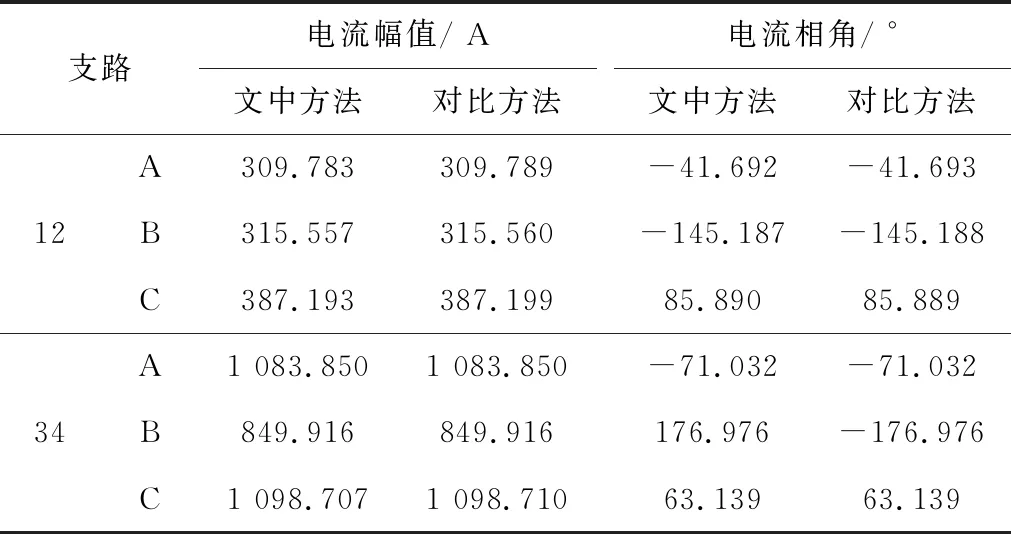
表3 不同方法潮流计算的支路电流
4 结束语
提出了一种计及中性点参数的变压器三相模型建立方法,解决了中性点不接地星形接线的变压器不能采用传统关联矩阵法建模的问题。该方法建立的变压器三相模型的关联矩阵包含中性点电气量,使得关联矩阵法可以应用于各种组别连接的三相变压器,而且可以通过转换矩阵从一个基本副边电压关联矩阵得到相同原副边连接方式下各连接组别的副边电压关联矩阵,进而得出变压器的电压关联矩阵。采用IEEE-4节点配网系统对本文方法进行验证,结果表明:所提出的计及中性点参数的变压器三相模型是正确的,应用于配电系统三相潮流计算可以非常方便地求出各节点电压及中性点电压。

