基于供排水工程系统优化的乡镇集中居住区规模分析

庄玉泽,辛乾龙,张礼华

(1.南京信息工程大学,南京 210000；2.中国电建集团西北勘测设计研究院有限公司，西安 710065；3.扬州大学，江苏 扬州 225000)

0 前 言

中国传统的农村居民居住区布局一般以耕作半径为依据，导致现有村镇居住区规模小，较为分散凌乱，农田集中程度不高，基础设施相对落后，进行基础设施和公共服务设施的规模建设面临较大困难。近年来，在我国新农村建设中，通过有序推进拆村并点工作，相应建设农村集中居住区，将原先分散居住的农村居民集中居住，以期合理利用土地，优化资源配置，节约基础设施和公共设施投资，提高土地的利用效率，提高民众生活水平[1-2]。

近年来，众多学者对我国拆村并点后集中居住区工作中的相关问题进行了大量研究，取得了丰硕的成果，其研究主要内容一般关注于集中居住区居民规模确定情况下，进行农民集中居住区居民满意度调查分析、景观设计、空间规划等[3-6]。同时，对于集中居住区、市政给排水工程问题，众多学者也提出了不少见解，一般聚焦于集中居住区居民规模确定情况下集中居住区给、排水管网线路布置、管径选择、管网漏损计算等[7-9]。但目前较少见到相关文献对农村拆村并点的农民集中居住区规模进行研究，也未见到在集中居住区位置确定条件下，寻求不同居住区合理规模，以此确定最小的给、排水管路管径，从而降低工程投资。因此，本文针对农村拆村并点工作中，不同居住区位置及总体拆迁居民数量确定条件下，以给、排水工程建设投资最少为目标函数，以各居住区居民数量为决策变量，一定给、排水标准下的给水流量、排水水量为约束条件，建立集中居住区适宜规模优化模型，并采用动态规划方法[10]进行求解，从而减少居民点给、排水管网工程投资，为新农村建设中拆村并点居住区工程建设提供参考。

1 居民区人口规划模型与求解方法

1.1 模 型

一定的居民区数量及规划总人口确定条件下，以满足该居民区给水和排水工程投资费用最少为目标函数，以给水站日可供水流量、单个居民点可居住人口、给排水管径选用规格为约束条件，建立数学模型如下：

(1) 目标函数：

(1)

(2) 总人口约束：

(2)

其中单个居民点居民人口约束：

[Pi,min]≤Pi≤[Pi,max]

(3) 总流量约束：

(3)

(4) 流速约束：一般给水管管道流速介于0.6 ～1.5 m/s之间，即0.6 m/s≤v≤1.5 m/s。

(5) 管径约束：Dmin≤D≤Dmax，其中，Dmin、Dmax分别为最小管内径、最大管内径，m。

公式(1)中:F为给水系统和排水系统工程总投资，万元，这里仅考虑不同管径对投资的影响，不考虑由于施工、管理等造成的投资变化；Di，给水管为第i号居民区的给水管管径，m，根据给水流量确定；Di，排水管为第i号居民区的排水管管径，m，根据规划排水流量确定；f(Di，给水管)为第i号居民区给水管管径为Di(标准管径)时相应工程投资，万元，由给水管管径-投资及给水管长度综合确定；f(Di，排水管)为第i号居民区排水管管径为Di(标准管径)时相应工程投资，万元，由排水管管径-投资及排水管长度综合确定；Pi、[Pi,max]、[Pi,min]、P分别为第i号居民区规划居住人口、第i号居民区最大允许居住人口、最小居住人口；规划总人口，人； 为第i号集中居住区实际给水流量，由该居民区实际居住人口及最高时用水流量确定，m3/s；Q为总给水流量，m3/s。

1.2 方 法

上述模型为在一定的总给水流量约束条件下，寻求不同居民区适宜居住人口，确定最小给、排水工程投资，可采用动态规划进行求解。

(1) 变量确定

将每一居民区人口作为一个决策阶段，按顺序编号，可采用逆向推行法计算。阶段变量由动态规划对变量的要求，确定居民区编号为i，i=1，2，…，k；决策变量根据各居民区规划人口Pi为决策变量，并进行离散，离散时，根据人口数量实际，可采用总人口数量的相应比例进行离散，如0、5%P、10%P、15%P，…，P；状态变量根据状态变量所具有的特性，选择按照居民区累加的人口λi为状态变量。

(2) 根据给水流量的不同，给水管、排水管管径采用下式进行计算：

(4)

公式(4)中：D为给水管道内径，m；Q为设计流量，m3/h；v为管内流速，m/s。

根据计算出的管径，并转换成标准管径，通过管径(内径)—单位长度投资(元)之间的关系，确定管道工程投资。排水管流量可采用给水管流量的相应比例进行估算，排水管采用无压流，其充盈度以0.8估算。

(3) 动态规划的求解

由动态最优化原理，将总人口 在各居民区间进行分配，以此寻求该阶段最小给水流量及相应给排水投资费用[6]。

1)N=1(第一阶段，即第1居民区)：

λ1=0，P1,P2,…,Pi。式中：P1,P2等为离散的阶段居民人口，Pi为第i时段总人口；状态转移方程如下：

f1(λ1)=f1(D1，给水管)+f1(D1，排水管)

(5)

公式(5)中:f1(D1，给水管)指给水管管径为D1，给水管时，给水管工程投资，元；其值的计算过程，首先根据居民用水定额q用水定额，与居民人数离散值，确定该阶段给水流量，即Q1=λ1q用水定额离散值，再根据公式(4)计算相应管径，并转换成标准管径，最后根据管径(内径)—单位长度投资(元)之间的关系，确定相应给水管工程投资。

f1(D1，排水管)指排水管管径为D1，排水管时，排水管工程投资，元；其值的计算过程，首先根据给水流量，以相应比例，确定排水流量，再根据公式(4)计算相应管径，并转换成标准管径，最后根据管内径—单位长度投资(元)之间的关系，确定相应给水管工程投资。

2)N=j(j=2～(k-1)阶段，k为居民点数)：

λj=0,P1,P2,…,Pi。式中：P1,P2等为离散的阶段居民人口(人)，Pi为第i时段总人口(人)，且Pi≤P；则：

fj(λj)=min{fj(Dj,给水管)+fj(Dj,排水管)

+fj-1(λj-1)}

(6)

状态转移方程：

λj=λj-1+Pj

(7)

3)N=k(最后一个阶段，即最后1个居民区)：

fN(λN)=min{fN(DN,给水管)+fN(DN,排水管)

+fN-1(λN-1)}

(8)

λN=0,P1,P2,…,Pi。式中:Pi为第i时段居民区总人口(人)；B为离散步长。

状态转移方程：

λN=λN-1+PN

(9)

则：

Fi=fN(λN)

(10)

2 模型应用

(1) 基本状况

以江苏某拆村并点区域为例，项目区迁居总人口为9 000人，按照常规居民点人口分布方法，规划将该9 000人平均安置于相隔10 km左右的3个集中居住点，每居民点3 000人。该3个集中居住区由一条主干给水管网集中供水，由于距离供水厂较远，中途通过增压站提升水压，该增压站最大供水水量130 m3/h，建设时考虑给水最大日时变化系数采用1.5。规划铺设给水管径分别为DN280、DN250、DN160；排水管网距污水处理厂距离约10 km，排水流量以给水流量的75%进行估算，排水管径规划分别采用DN110、DN160、DN200，管网工程投资(不考虑施工、管理等其它费用)按照“江苏工程造价网”(2021年5月)进行计算，整个给、排水管网总投资1 017万元。

该3个居民区建设时，考虑到未来的发展，同时考虑到居民意愿和分布需求，每集中居住点均留有一定的扩展余量和最低居住人口要求，可居住人口上限为最大不超过5 000人，最小不低于1 000人。项目区示意见图1。

(2) 根据“江苏工程造价网”(2021年5月)，供排水管(PVC-U管，江特牌)不同规格时单价见表1。

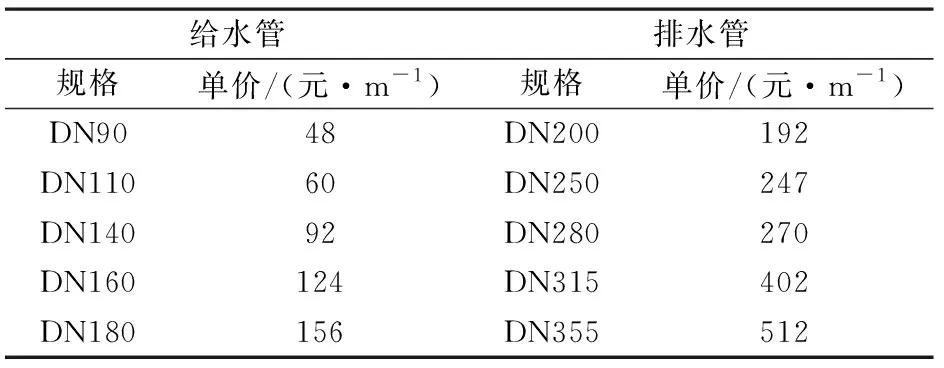
表1 管材单价

(3) 根据上述基本条件，为减少管网工程投资，合理分布每个居民点人口数量，建立数学模型如下：

1) 目标函数：

(11)

2) 总人口约束：

(12)

3) 单个居民点人口约束：

1000≤Pi≤5000 (i=1、2、3)

(13)

4) 总流量约束：

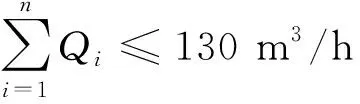
(14)

5) 流速约束：一般给水管管道流速介于0.6～1.5 m/s之间，即0.6 m/s≤v≤1.5 m/s。

6) 管径约束：Dmin≤D≤Dmax，其中Dmin、Dmax分别为最小管内径、最大管内径，m；一般集中居住区供排水管路管径为90～500 mm之间。

式中各参数的意义参见1.1部分。

(4) 结论与分析

采用前述动态规划优化方法对集中居住区规模进行优化，离散步长1000人，并以此确定相应最优的给排水管道工程投资，结果见表2前3行。

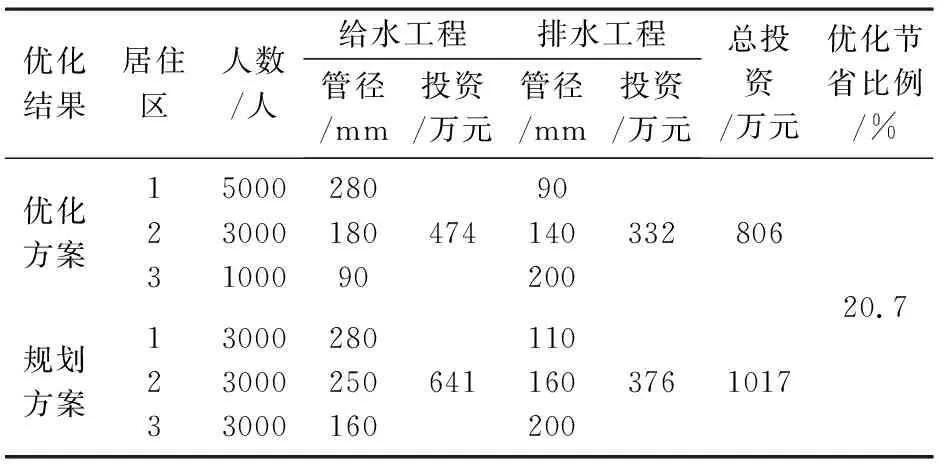
表2 集中居住区供排水方案结果

将上述优化结果与该3个集中居住区原规划方案(每居民区3 000人)进行比对，结果见表2。可见当集中居住区位置、给水、排水距离均已确定情况下，优化方案相较于规划方案，管道工程投资节约211万元，节省比例达20.7%，说明本方法应用于农村集中居住区规模优化，可有效减少给排水管网投资，取得较好的经济效益。

3 结 论

(1) 本文针对现行江苏撤乡并镇工作中居民点的规模问题，建立了一定的居民区数量及规划总人口确定条件下，以满足该集中居住点给、排水工程投资费用最少为目标函数，给水站日可供水流量、单个居民点可居住人口、给排水管径选用规格为约束条件的数学模型，并采用动态规划方法进行求解，从而确定适宜的农村居住区规模；通过实例分析可知，优化方案相较于原规划方案，给排水管网工程投资节省20.7%，说明该方法可有效减少工程投资费用，可为其它不同类型的集中居住区工程规模的确定提供借鉴。

(2) 居民集中居住区规模优化结果受离散步长影响较大，本文实例采用1 000人作为离散步长，如需取得更精确的优化结果，可进一步减小离散步长。

(3) 本文污水处理量采用按最大给水流量的相应比例进行计算，优化结果显示，越靠近给水点，居民集中居住区规模在允许范围内可适当增大，其后其他居民集中居住点规模相应减小。

(4) 集中居住区规模确定影响因素较多，如拆村并点后群众耕作半径、居住意愿等，均会对不同集中居住区规模产生较大影响。本文在不考虑其他影响因素的前提下，由于3个集中居住区给排水间距相同，但其它类似工程中，由于集中居住区位置不同，给排水工程路线、距离变化较多，其优化结果也会产生相应变化。