运用“数形结合”提高学习效度

佘芳芳

运用“数形结合”提高学习效度

佘芳芳

（莆田市城厢区霞林学校，福建莆田351100）

在数学学习过程中利用“数形结合”的思想研究数学问题，把晦涩的数量关系用简单明了的几何图形来展现，又或是将图形的几何属性通过严密精准的数量关系阐明出来，都能够让概念理解走向深刻，直观可见地理解算理，更加凸显数学本质，解决问题形象化、多样化，从而提高问题解决的逻辑思考和推理判断水平，提升数学学习效度。

数形结合；数学思想；学习效度

“数形结合”是一种重要的数学思想，在辅助学生探究解题方法中充分发挥了其优势，已经成为了引导学生分析数学问题的重要手段之一。在探索数学问题的解答方法时，学生可以依靠“数形结合”思想的独特特点，把晦涩的数量关系用简单明了的几何图形展现，又或通过数字的精确性特点表示形的几何属性，能够让概念理解走向深刻，直观可见地理解算理算法，更加凸显数学本质，解决问题形象化，从而提高问题解决的逻辑思考和推理判断水平，帮助学生提升数学学习效度。

一、以形助数，让概念理解走向深刻

正确理解数学概念是数学学习的前提与基础，概念的抽象性又往往成为学生正确理解概念的一道槛。因此，概念教学中，教师如果能够在学生经历知识产生的过程，以形助数，借助图形表征概念的基本特征，使抽象的数学概念直观化、形象化，那么，学生就容易实现对概念本质特征的深刻理解，深度建构概念模型。

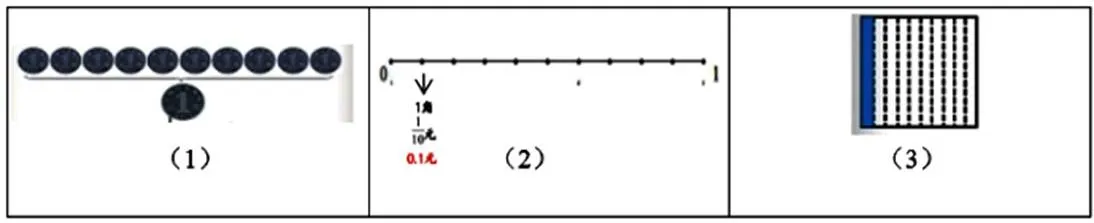
图1

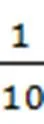
二、以数化形，让算理算法直观可见

传统计算教学的重点仅仅停留在掌握算法、具备一定的运算技能这种较浅显的层面上，然而这并不是运算能力的全部内容，良好的运算能力应该是运算技能和数学思考的综合体，是引导学生养成数学核心素养的重要基石。只有让算理算法更加直观可见，才能让教学的重点得到明确，将数学课程中的抽象知识能够更加直观地展现出来，教师可以将算理与算法通过实践进行结合应用，保证学生能够在阅读题目的第一时间探寻到题目的真正内涵，让学生能够通过不同算法的复合运算，寻找到合理的数学问题解决途径，这样才能有效地提升数学问题解决的速度，将更多的数学理念进行融会贯通，让学生寻找到最合适的解题路径。学生掌握算法的前提是要让其理解算理，使学生积极探索其中蕴含的数学原理，达到“知其所以然”的程度，提升自身运算水平。因此，教师在教学过程中要把算理的理解作为教学的重点内容之一，可以采用直观的几何图形阐明抽象的算理内容，借助图形的直观性有效地帮助学生充分理解运算的基本道理，为提炼算法做基础，实现算理与算法融通。

探究：

图2

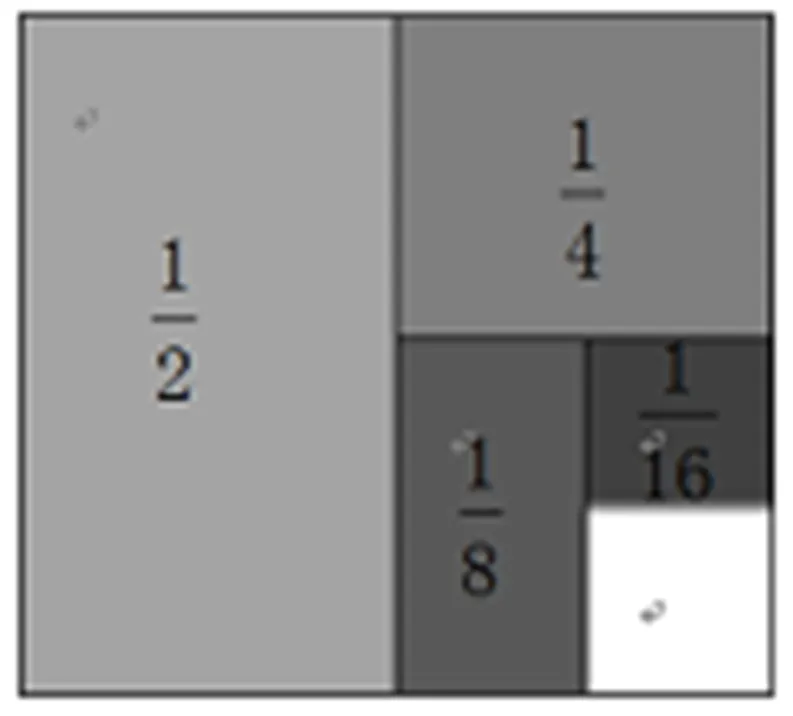
图3

三、以数辅形，让数学本质更加凸显

统计图是一种用直观图形表达数据整理统计结果的记录方式，它充分体现了数形结合思想在实际生活的运用。例如，《折线统计图》的教学，教师先通过条形统计图的直条到点再到线的演变，使学生明白折线统计图是如何产生的，然后再引导学生体会和总结折线统计图的特点：折线统计图中用点描述数量的多少，用线来描述数量的增减变化情况。接着引导学生思考：观察折线统计图时是否只需要关注图呢？教师随即给出一幅纵轴缺少数据的反映某市一年气温变化的折线统计图（如下左图）。让学生猜测：该折线统计图反映的是四季分明的杭州，还是四季如春的昆明，还是常年低温的哈尔滨？学生仅从折线的陡缓判断，必定认为是四季分明的杭州。

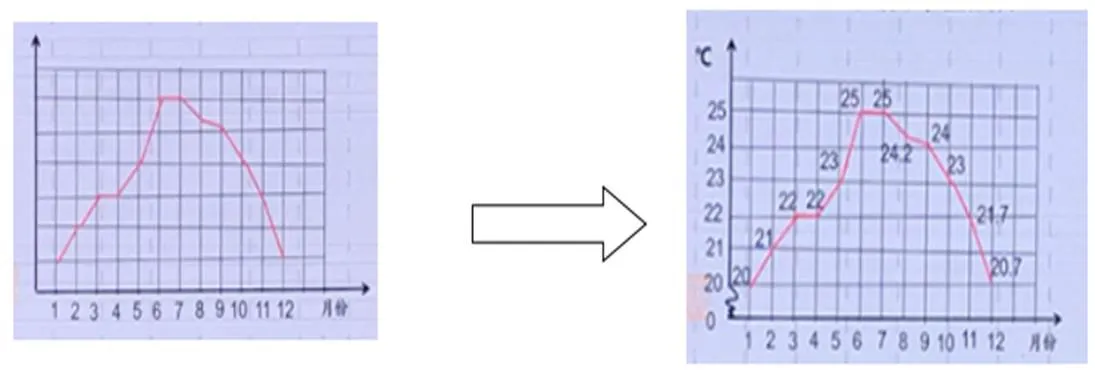
图4

正当学生脱离数据产生认识偏差时，教师补充纵轴数据（如图4右），学生立马感受到单看线的陡缓是不够准确，需要结合数据进行判断，真正体会“形少数时难入微”。接着启发学生思考，怎么让人一看就能准确判断出该折线统计图反映的四季如春的昆明的一年温度，学生自然想到修改纵轴数据，让折线更平稳一些，把左图变成右图形式。

图5

（气象提醒：我市气温变化比往年要大，请广大市民留心关注气温变化。）

（旅游宣传：这里四季如春，气候宜人，欢迎您来昆明。）

最后，通过昆明旅游局和气象局从统计的功能性出发，对两幅折线统计图进行了不同的选择，使学生感受绘制统计图时数形结合的必要性，深刻理解统计图的本质与作用。

四、数形结合，让解决问题直观形象

解决问题是小学数学课程的重要内容。传统的应用题教学，教师多是采用题海战术，往往导致学生生搬硬套、思维僵化，一旦数量关系变化就可能束手无策。教师在数学问题的教学过程中要时刻提醒学生用“数形结合”的思想解决问题，当遇到复杂的数学问题时要让学生自己尝试着画出图形，将题目条件通过几何图形展现出来，以此寻找解题的突破口。所以当前的数学教学课程中需要一种有效的方法将一些复杂的知识进行转化，将更多抽象的条件以直观的形式让学生进行观察，这样才能真正提高学生解题的能力，让学生的解题速度得到全面的提升。在当前的教学课中应当尝试将这些题目中的关键信息表现出来，让学生能够精准地抓住数学问题的重点，找到高效率的解题方式，让更多学生能够通过这种方法快速寻找到解题的关键要素，在脑海中构建起完整的数学模型。通过这种教学方法，可以让学生的解题能力达到优化，学生也能够通过这种教学方法提升自身的学习能力，让他们养成自主探究的习惯。将题目中的文字条件转变成直观清晰的几何图形，采用“数形结合”方法辅助学生梳理题目中的数量关系，深入理解题目含义，找到解决问题的关键突破口，有效构建数学模型，解决问题能力自然会获得提升。

例如，行程问题的基本数量关系是“速度×时间=路程”，对此学生虽然熟悉，却因为运动物体数量、时间、地点、方向、运动结果的变化，构成的问题数量关系多种多样，学生解题时常常不知从何下手。教师如果能引导学生依题意画图，借助几何直观，通过数形结合，就比较容易理解题中的数量关系，找到解决问题的策略。以如下题目为例：已知A、B两地之间的距离为300千米，现在，甲车和乙车同时出发且甲车速度：乙车速度=4:3，其中甲车每小时走过的路程为80千米，问2小时后两车相距多少千米？本题没有规定两车的运动方向，是道开放题，学生能够借用如下的画图策略（如图6），可以很好地理解有三种运动情况。

图6

（1）两辆车分别从A、B两个位置相对（相向）行驶。

数量关系式：A、B两地的距离-两车已行路程之和=两车相距的距离

300-（80+60）×2=20（km）

（2）甲、乙两车在同样的位置朝着同一方向出发。

数量关系式：甲车走过的路程-乙车走过的路程=两车相距的距离

80×2-60×2=40（km）

（3）甲、乙两车在同样的位置朝着相反的方向出发。

数量关系式：甲车走过的路程+乙车走过的路程=两车相距的距离

80×2+60×2=280（km）

在解决此类路程问题时，线段图是一种非常有效的辅助工具，学生可以画出线段图分析车辆的行驶路程，明确三种不同运动方向，甲、乙两车2小时后的位置关系，逐个厘清蕴含的数量关系。采用“数形结合”的数学思想分析数学问题、探究题目结果可以帮助学生更好地理解题目意义，打开学生解题思路，培养学生的数学思维。

华罗庚先生曾说过：“数形结合有百般的好处。”这就深刻地阐明了“数形结合”这一重要数学思想的重要性和优势所在。在日常的数学教学中，只要教师注重引导学生利用“数形结合”的思想分析、研究数学问题的解题思路和技巧，化抽象为具体，就一定能够帮助学生挖掘题目中的隐含信息，打开学生的解题思路，引导学生积极主动地探索问题结果，学生的数学学习定会走向深刻，实现深度学习。在我国的数学教学课堂上最常见的问题便是教师的教学方法并不合理。对于数学教学工作而言，这些教学方法很难让学生产生对数学的兴趣，如果学生缺少兴趣很容易失去学习的动力，所以教师应当以学生的兴趣激发进行课程的设计，降低数学学习的门槛，让学生能够将一些复杂的理论知识用简单明了的几何图形进行展现，这样更有利于激发学生的学习欲望，让他们能够在自主探究的模式下高效率地进行学习。教师应当根据学生的特点设计出更加完善的教学方案，让更多学生能够利用数形结合的方法梳理题目中的数量关系，并且将自己所学的解题方式带入题目当中，让学生的学习水平得到全面的提升，学生能够更加灵活地运用知识解决问题，将更多复杂的知识以直观的形式进行解答，实现学习水平的全面提升。

[1] 宋梅娟.数缺形时少直观,形少数时难入微[J].明日,2018(19).

[2] 徐惠.合理“嫁接”数与形促进学生数学理解[J].小学教学设计,2014(29).

[3] 林文清.几何直观在“数与代数”教学中的巧妙运用[J].青海教育,2018(10):2.

[4] 袁晓萍.让数据分析成为一种思维习惯——“统计里的秘密”教学实践与思考[J].小学数学教育, 2018(12).

G622

A

1002-7661(2022)11-0151-03