卫星USB 测控副载波同步算法研究*

张士伟，邢斯瑞，常俊德，金宇婷，赵 博，沈晨阳

(长光卫星技术有限公司，吉林 长春 130000)

0 引言

统一S 波段(Unified S-Band TT&C System，USB)测控是目前卫星常用的一种测控方式，对于卫星测控接收机来说，要想正确稳定实现遥控指令的接收，载波同步、跟踪技术是关键，如果同步性能不佳导致误码将使指令变成无效指令，影响卫星的测控效果。

传统载波同步基于锁频环+锁相环的方式，但在实际工程应用中，由于通信距离非常远，接收信号弱，信噪比较差，锁频环跟踪载波频率时振荡较大，锁频环跟踪稳定后转锁相环时，无法保证频差百分百处于锁相环的捕获带内，导致锁相环无法锁定，需要重新进行载波捕获，增加了捕获时间，降低了捕获概率，不适合卫星测控通信的应用[1]。本文给出了一种快速傅里叶变换结合锁相环(FFT+PLL)的方法，可以很好地适用各种卫星测控的应用场景。

1 参数设计

USB 测控将遥控副载波通过调相(Phase Modulation，PM)调制到载波上，一般USB 测控要求的载波多普勒捕获范围为±115 kHz，多普勒变化率为±32 kHz/s[2]。对接收信号下变频至零频并用250 kHz 采样率的1 024 点FFT 对其进行分析，分析频率范围为±125 kHz，分析时间为4.096 ms，频率分辨率为244 Hz，然后通过载波PLL1实现载波的跟踪，解调出副载波信号。当载波实现跟踪后，副载波存在的多普勒频率为：

其中，fsubc_d为副载波多普勒，fsubc为副载波频率，fc_d为载波多普勒，fc为载波频率。计算可得副载波残留的多普勒频率小于±10 Hz，多普勒变化率在±0.2 Hz/s 之间，留有余量设计PLL2 的快捕带为±50 Hz。

2 数字PLL 设计

跟踪PLL 本质是数字二阶锁相环，是由模拟二阶锁相环等效而来，当采用理想积分滤波器时模拟PLL 的S域闭环传递 函数为[3]：H(s)=通过双线性变换，将系统闭环传递函数转换为Z 域系统闭环传递函数[4-6]，如下所示：

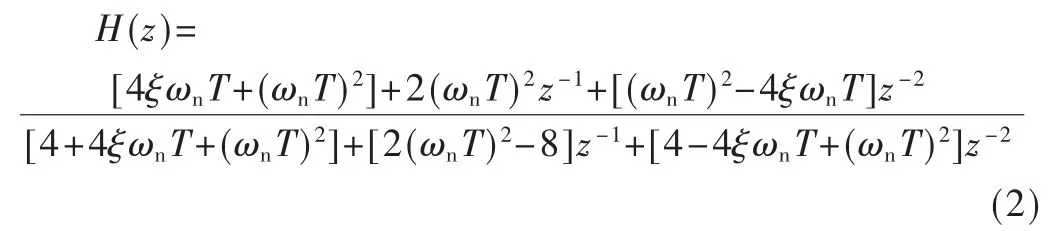
其中，ξ 为阻尼比，ωn为无阻尼振荡频率，T 为环路周期。

数字二阶锁相环由鉴相器、环路滤波器和直接数字合成器(Direct Digital Synthesizer，DDS)组成，准确地建立环路滤波器、DDS、鉴相器的Z 域传递函数对于建立系统闭环传递函数至关重要。在构建二阶环相位模型时，选择具有正弦鉴相特性曲线的鉴相器，该鉴相器的相位增益为1，鉴相输出在±1 之间。下面对环路滤波器和DDS 的Z 域传递函数进行建模。

2.1 DDS 的Z 域相位传递函数

DDS 的组成原理框图如图1 所示[7-9]。

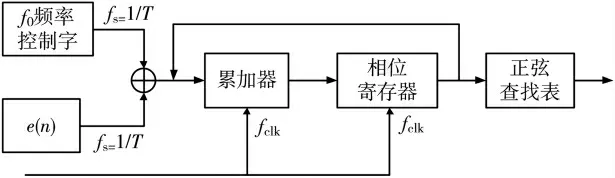
图1 DDS 原理框图

误差信号e(n)引起的DDS 输出频率为：fout=e(n)×fclk/2N，其中fclk为DDS 的工作时钟，相位控制字长为N。假设环路闭环周期为T，即每隔T s 对e(n)采样一次去修正中心频率f0。DDS 的Z 域相位传递函数仅考虑由误差信号e(n)引起的相位变化，nT 时刻输出的相位如下所示：

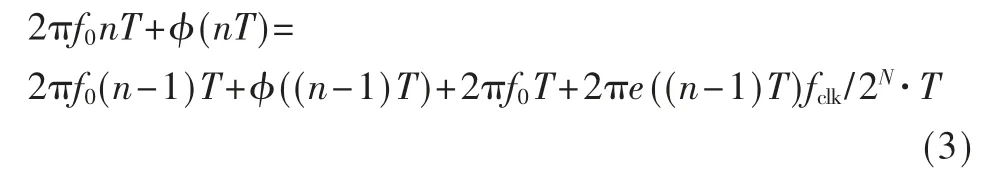
对式(3)等式两边消去载波标称频率项，并改写为离散形式如下：φ(n)=φ(n-1)+2πe(n-1)fclk/2N·T，则DDS 的相位Z 域传递函数为：H(z)=2πfclk/(2N(z-1))·T，DDS 的相位增益为KDDS=2πfclk/2N·T。

在设计中fclk=3.5 MHz，环路闭环周期选择32 个1/fclk，N=32，则DDS 的传递函数为H(z)=4.61×10-8/(z-1)，DDS 的相位增益KDDS=4.61×10-8，输出8 kHz的副载波[10]。

2.2 数字环路滤波器

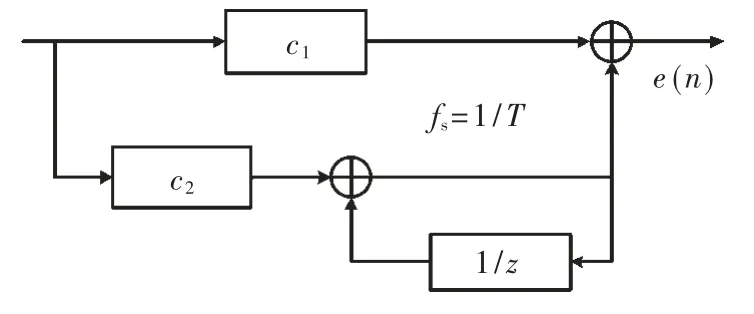
图2 数字环路滤波器Z 域传递函数框图

由每个组成部分可以推出系统的闭环传递函数如下所示：

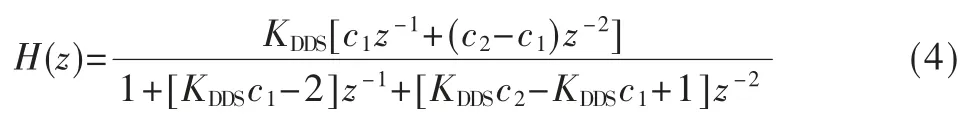
其中，c1和c2是数字环路滤波器直通支路和累加支路的增益。在保证模拟和数字的闭环传递函数极点相同，可以推出：

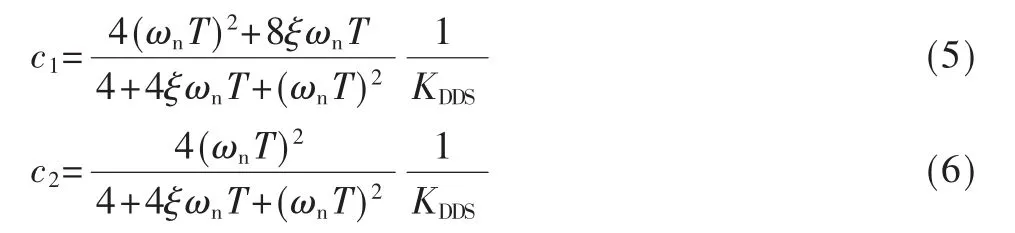
综上，整个PLL 锁相环Z 域传递函数如图3 所示[13]。

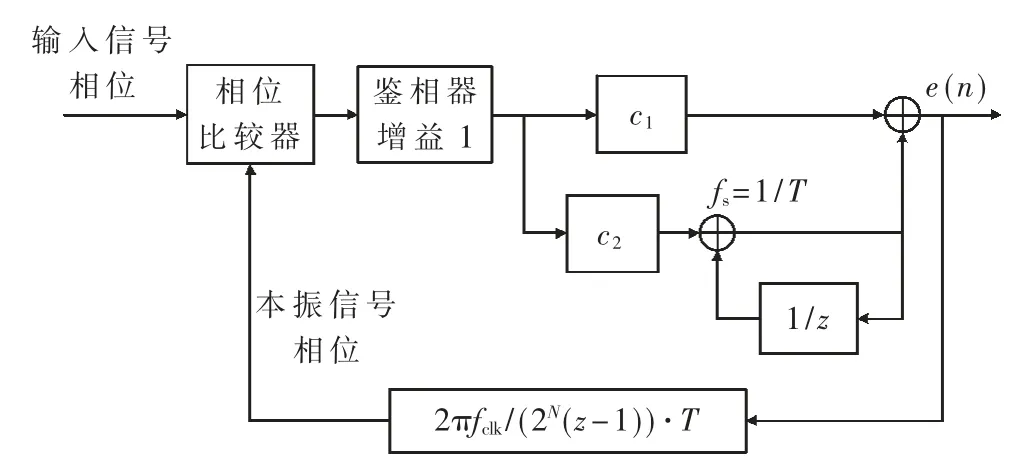
图3 数字PLL 相位模型框图

选择ξ=0.707，±50 Hz 快捕带对应的环路无阻尼自振角频率为ωn=222.18 rad/s，综上环路滤波器系数c1=613 567，c2=88。数字域环路滤波器系数所对应的模拟域系数τ1=T/c2=1.04×10-7，τ2=c1×T/c2-T/2=0.006。

3 数字PLL 分析

PLL 分析包括稳定性分析、信噪比、快捕带及快捕时间、捕获带及捕获时间、同步带及跟踪速率等分析。下面分小节进行介绍。

3.1 稳定性分析

从Z 域对系统的稳定性进行了分析，首先求取了系统的Z 域传递函数闭环极点为0.9986+0.0029i，0.9986-0.0029i，极点位于单位圆内，可以判断系统是稳定的。为了对系统的稳定程度进行量化，绘制了系统的波特图，如图4 所示，包括系统的幅频特性曲线和相频特性曲线，从幅度裕度和相位裕度两个方面进行了求证[14]。其开环幅度穿越频率为55 Hz，与快捕带一致，相位裕度为65.4°，可以看到系统具有良好的稳定性。

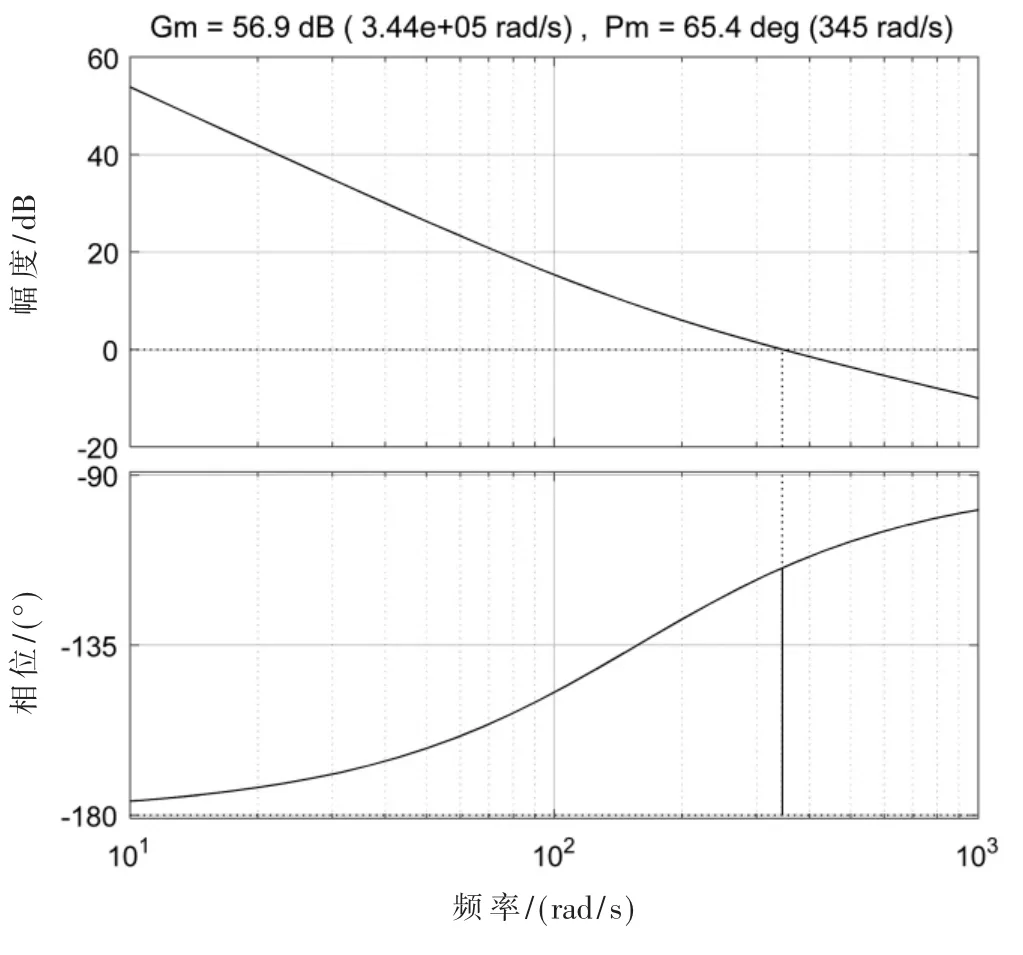
图4 系统波特图

3.2 PLL S/N0 分析

在不同的应用场合，对锁相环恢复的相位误差有不同的要求，该误差与输入信号的信噪比直接相关，经分析，恢复的载波相位标准差为：

其中，2BL为环路的带宽，S/N0为信号功率与噪声谱密度比。在不同的环路带宽下，相同的同步精度所需的S/N0也不同，具体如图5 所示，可以根据实际情况进行参数选择。

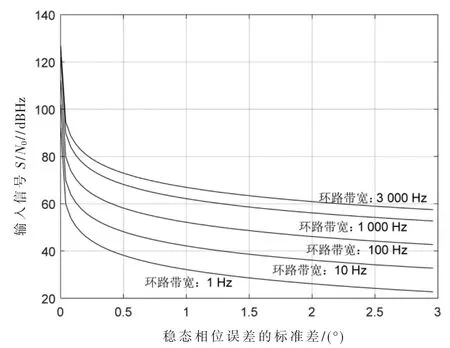
图5 S/N0 与稳态相差

3.3 快捕带及快捕时间

快捕带与环路滤波器的设计是息息相关的，鉴相器的输出是幅度为1 的差拍信号cos(2πΔft+φ)，其中Δf 为输入信号频率和本振信号频率的差频，如果该差拍信号经过环路滤波器得到的误差信号控制DDS 得到的频率增量为这个差拍频率，则该差频为PLL 的快捕带，通常PLL 的工作频率范围限制在快捕带内[15]。环路滤波器的频率响应为：

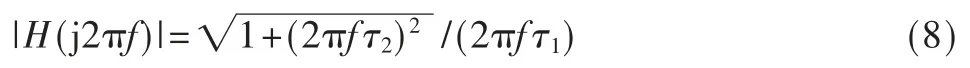
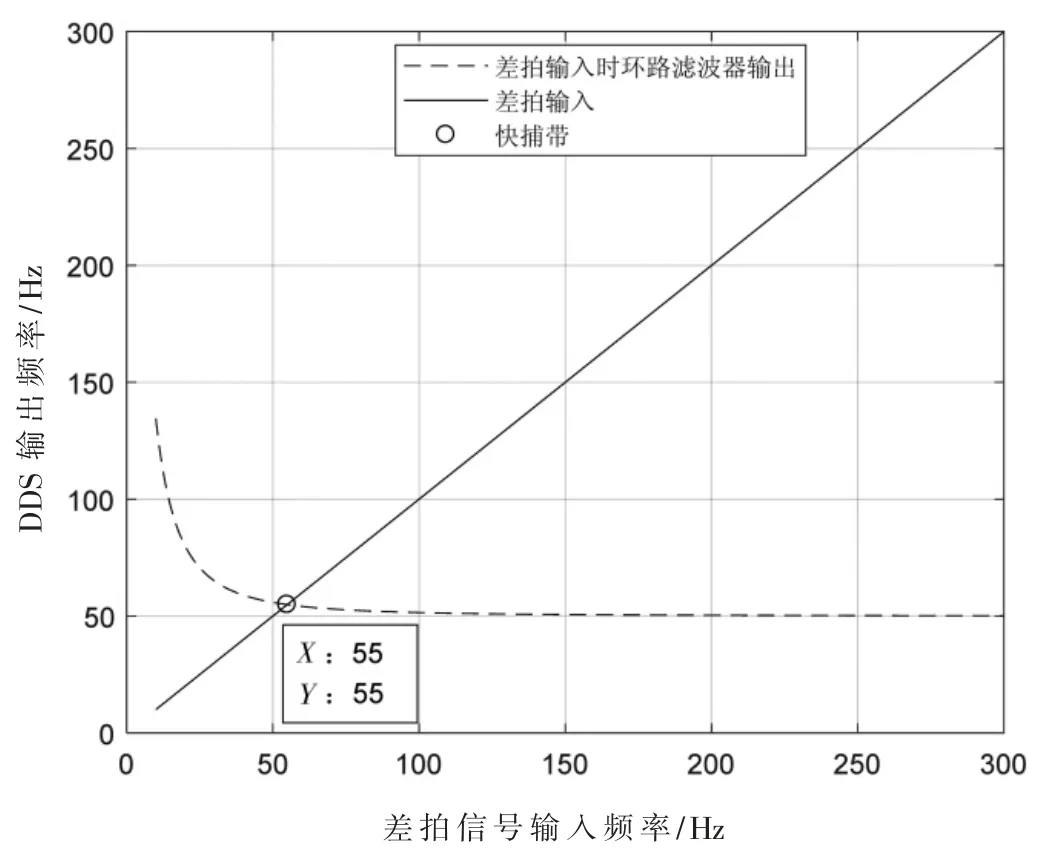
图6 快捕带的仿真结果

当响应的包络线进入允许误差范围内之时，二阶系统的单位阶跃响应曲线必然也处于允许误差范围内，因此通过如下公式可求得系统的过渡时间(即快捕时间)：

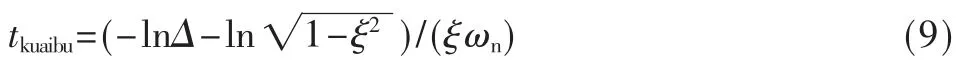
当Δ=1%时，tkuaibu≈5/(ξωn)=0.031。图7 为仿真的结果，快捕时间为0.031 s，可以看到实际仿真结果与理论一致。

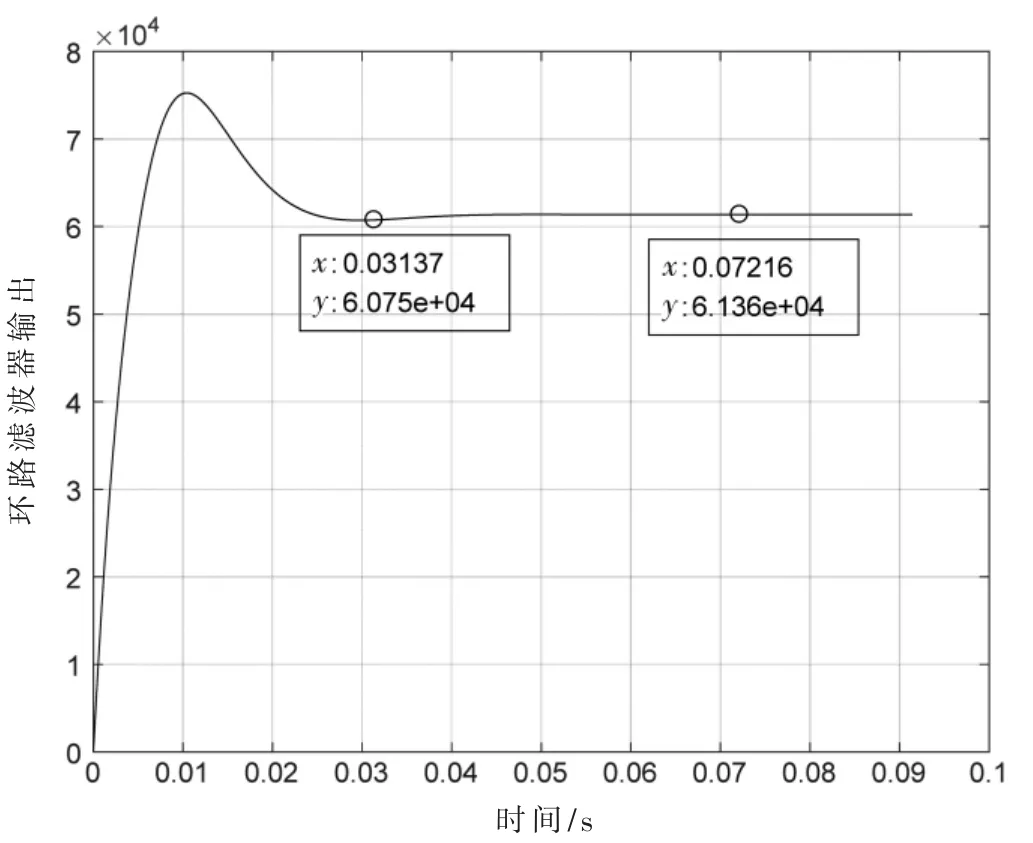
图7 输出频差50 Hz 时误差响应曲线

3.4 捕获带及捕获时间

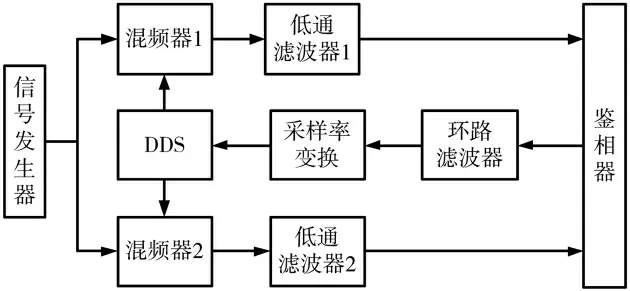
图8 频率模型

图9 中给出了初始频差从200～1 100 Hz 时的频率牵引时间，可以看到相位模型和理论计算的结果一致，频率模型由于在环路处理时引入低通滤波等额外的延迟环节，使pull-in 时间增加。

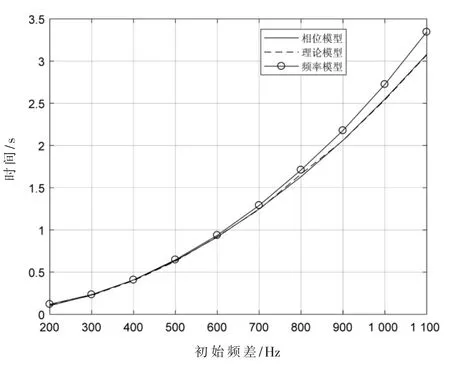
图9 频率牵引时间与初始频差

图10 中给出了理论及引入4、8、12、16 阶延迟环节pull-in 时间情况，为了减少频率牵引时间，可以使用阶数较小的IIR 滤波器以减小延迟环节加速捕获时间。

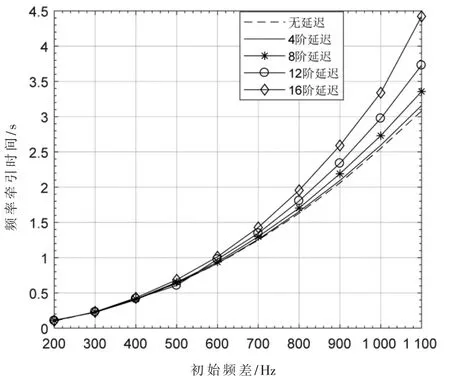
图10 延迟环节对频率牵引时间的影响

3.5 同步带及最大同步速率

在环路锁定时，缓慢增加固有频差，直到环路失锁，能够维持环路锁定的最大固有频差称为同步带。环路锁定时，瞬时频差等于0，控制电压为直流。对于正弦鉴相特性的环路，有Δω0=KDDSH(j0)sin(θe(∞))，其中θe(∞)为稳定相位误差，当θe(∞)=π/2 时，得到维持环路锁定的最大固有频差，所以理论上二阶环的同步带可以∞。对于正弦鉴相特性的锁相环路，当输入信号为频率斜升信号时其相位为θI(t)=0.5×R×t2，R 为频率扫描速率。环路锁定后稳态相位误差为一固定值θe(∞)=arcsin(R/)，即稳态相差与扫描速率R 和系统的无阻尼自振角频率相关。当扫描速率小于时θe(∞)=arcsin(R/)方程有解，也就是理想二阶环的最大同步扫描速率为Rmax=，远大于副载波多普勒变化率±0.2 Hz/s。

综上，该算法快捕带为±55 Hz，快捕时间仅为0.03 s，相位裕度为65.4°，在输入信号的信号功率噪声谱密度比S/N0=60 dBHz，相位误差标准差约0.5°。

4 结论

本文给出了一种卫星USB 测控副载波同步算法，该算法具有捕获快、跟踪精度高、稳定性好、易于数字化实现的特点。同时该算法具有通用性，仅需根据要求适当调整参数即可，已在多颗吉林一号卫星的测控系统中得到应用。