基于Copula 函数的瓯江设计潮位过程研究
林乐曼,周倩倩
(1.温州市水利规划发展研究中心,浙江 温州 325000;2.温州市水利局,浙江 温州 325000)
1 问题的提出
设计潮位过程线是指相应于一定防御标准的潮位过程线,是河口海岸地区防洪排涝水动力模型计算的重要边界条件。从防洪潮角度,高潮位毋庸置疑是决定设计潮位过程线至关重要的元素,但是潮差作为其重要组成特征,同样也是排涝设计计算中的重要要素。科学地推求设计潮位过程线,对于确定工程规模以及识别分析工程防护风险程度而言,具有重要意义。
关于设计潮位过程线的计算方法,现行规范推荐的是同频率设计法。该方法规避了同倍比法因基面不同而导致计算结果不同的问题,但是由于该方法是基于高潮位和潮差同频率的假设,易出现设计潮差与实际潮差偏差较大乃至不合理的情况,缺乏对高潮位和潮差之间相依性的考虑,存在主观性和随意性。
近年来,得益于Copula 函数的发展,一些极端水文事件变量的相关性研究也有所进展。在设计潮位过程线的研究中,刘学等[1]利用Copula 函数建立年最高潮位和年最大潮差的二维联合分布,并计算重现期,提出一种以高潮位为控制,结合同现重现期推求设计潮位过程线的方法。周月英等[2]将联合分布应用于珠江口设计潮位过程线的计算,但是论文中采用的数据为年最高潮位与年最大潮差序列,事实上样本选取时就破坏了潮位与潮差的相关性,结果并不能真实反映潮位的相关特性。薛晓鹏[3]等建立年最大潮位与同期潮差,保留了数据的相关性,采用最可能组合法计算设计高潮位条件下的最大潮差,并推求出设计潮位过程。为验证该方法在瓯江的应用效果,本文拟采用基于Copula函数建立瓯江年最高潮位与同期潮差的联合分布,并以高潮位为控制要素,采用条件最可能组合法,计算设计高潮位条件下概率最大的潮差,最后典型放大得到设计潮位过程。
2 基于Copula 函数联合分布的设计潮位过程分析方法
根据Sklar 定理,存在一个Copula 函数C,能够使多个边缘分布聚合在一起构建出多维联合分布,若边缘分布都是连续的,则C唯一。其数学表达式为[4]:
式(1)中:F(x1,x2,…,xd)表示联合分布函数;ui=Fxi(x)是随机变量的边缘分布函数,ui∈[0,1] ;x1为设计高潮位,m;x2为同期潮差,m;d取2。
通过对C(u1,u2)函数求导,可得相应的Copula 联合概率密度函数c(u1,u2),公式如下:
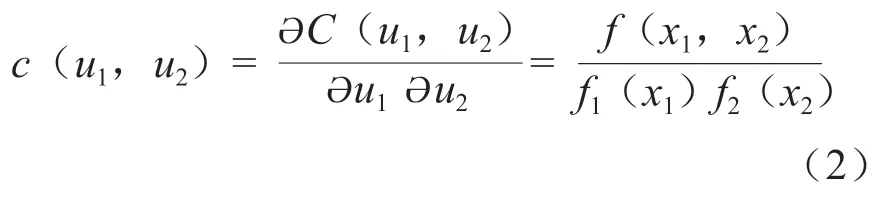
联合分布的参数估计可采用边际函数推断法[4],即求解参数通过2 个步骤完成,首先求解边缘分布参数,然后根据极大似然原理由Kendall 秩相关系数推求出Copula 函数的参数。
2.1 边缘分布建立
边缘分布Fxi(x)即极端水文事件分析计算中经常使用的单变量分布,本文采用标准规范推荐的P-Ⅲ型分布作为高潮位、同期潮差的边缘分布[5],概率密度函数公式为:
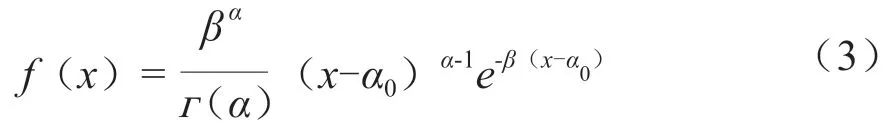
式(3)中:α=;β=EXCVCS/2;α0=EX(1-2CV/CS);EX、CV、CS分别为样本的均值、离差系数、偏态系数,一般可通过矩法结合目估适线法进行估计。为检验边缘函数的拟合效果,采用卡方检验等方法[4]。
2.2 二维联合分布建立
Copula 函数的类型和形式有很多种,Achimedean Copula 作为Copula 函数中重要的一簇函数,其结构简单,形式丰富,得到广泛应用。本文采用Gumbel-Hougaard、Clayton、Frank、Ali-Mikhail-Haq Achimedean Copula 函数分别建立联合分布,并通过多方案比选的方式来确定最优Copula 联合分布[4],表达式见表1。表1 中,τ为Kendall 秩相关系数,公式为:

表1 3 种Achimedean Copula 函数表达式表
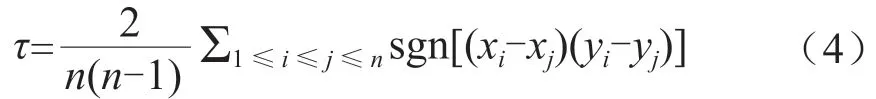
式(4)中:xi,xj,yi,yj为实测点据;n为样本系列容量。
采用BIC 法(Bayesian information criterial)比选最优Copula,BIC 统计量是描述理论联合分布值与经验联合分布值之间差距的统计值,也就是说统计量越小,拟合效果越好,公式如下:
例如,在讲解《卖火柴的小女孩》一课的过程中,当学生对课文内容有一定了解之后,教师就可以将角色扮演这一形式引入进来,让学生以小组为单位,对课文进行改编,并将改编好的课本剧以角色扮演的方式进行情景再现,在这其中不仅可以彰显学生的主体地位,也能使学生站在不同的视角下对文章内容进行重新审视,使其的理解程度大大加深,使教学效果得以进一步的深化。
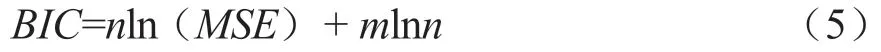
式(5)中:m为Copula 参数估计数;MSE=;Pc、P0分别为Copula 多元联合分布计算值、联合分布经验值。
最后采用CPI Rosenblatt 转换法对建立的最优模型进行拟合优度检验,统计量选择A—D,若统计观测值小于置信水平为α的临界值,则认为拟合效果较好,否则分布不合理[4]。
2.3 设计组合风险分析
在一般的防洪挡潮工程规划建设中,高潮位是影响安全的主要因素。实际工程中,发生一定设计标准的高潮位时,潮差往往存在多种可能性,而它们出现的概率也不尽相同,相应概率的风险情况也不同。研究和掌握不同设计标准高潮位下,高潮位和潮差的组合概率风险值对于工程防汛风险分析评估具有重要意义。在满足设计高潮位x1条件下,将潮差超过x2发生的概率作为其组合风险率[3],数学表达式为:
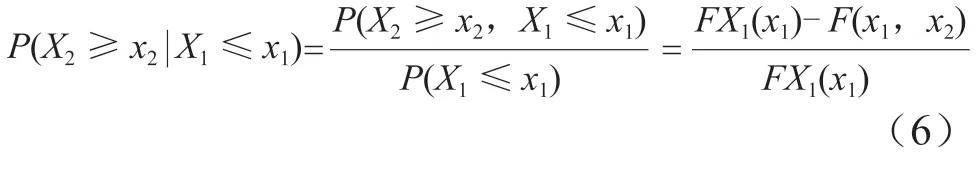
2.4 条件最可能组合
理论上潮位和潮差的组合情况有无数种,且发生概率不同,工程中往往比较关心的是大概率事件。对于设计潮位过程而言,特别在防洪排涝设计中,我们往往以设计高潮位做为控制要素,基于此,本文重点研究特定重现期的设计高潮位和条件概率最有可能发生潮差的组合。条件概率最可能组合定义如下:当出现设计高潮位时,最可能出现的潮差,用数学公式可表达为:

式(7)显然是一个非线性最优化问题。由于本文中u2为x2的P-Ⅲ型概率分布函数,其值一般可用数值积分近似求解,无显式函数表达式,故无法通过函数微分方式直接求解fx2 |x1的极值点,而遗传算法在求解非线性最优化问题中表现出色[6],可通过生成一定数量的个体,以数值积分的方法求得分布函数值u2,继而计算出由fx2 |x1构建的适应度函数,再经过一代代的交叉、选择、变异、淘汰、遗传等操作,最终找到最优解。因此,本文尝试将遗传算法应用于条件最可能模型的求解。
遗传算法求解的关键问题设置如下:①种群和种群规模。种群即所有个体的集合,x1k,x2k也就是个体,又称为决策向量,个体数量又称为种群规模(POP)。②个体编码方法。采用实数编码,考虑潮位实际情况,将上下限设定为各变量在TP=1.000 001 a、100 000 a 时相应的边缘分布反函数值。xi=ximin+rand*(ximax-ximin),其中,ximax,ximin分别为变量xi的取值上下限,rand为[0,1]的随机数。③适应度函数。极大值优化问题,选用负构造法构造适应度函数g(x),即g(x)=B-fx2 |x1,其中,B为目标函数fx2 |x1界限的保守估计值。④停止准则。采用最大迭代次数停止准则。
3 瓯江设计潮位过程计算
3.1 基于Copula 函数的联合分布
3.1.1 边缘分布
选取瓯江温州站1970—2018 年潮位数据,根据年最大法(AM 法)筛选年最大高潮位和同期相应潮差,共获得49 组样本数据,假定年最高潮位和同期潮差服从P-Ⅲ型分布,采用矩法结合目估适线法估计参数,并用K-S 检验法检验假设的合理性,计算结果见表2。
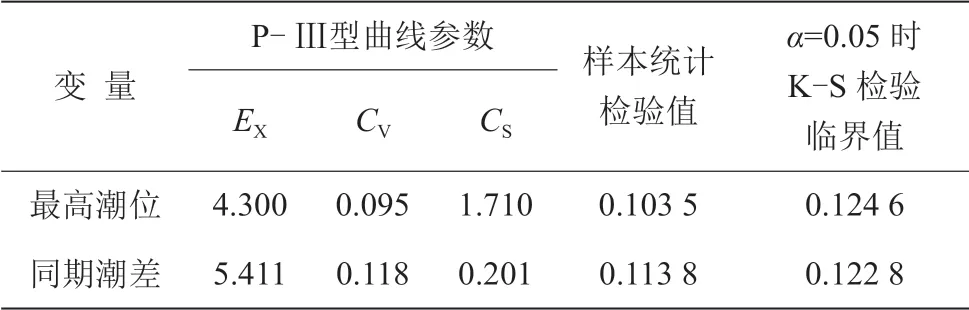
表2 边缘分布函数参数计算结果表
由表2 可见,样本统计检验值小于K-S 检验临界值,即上述建立的边缘分布通过了显著性水平α=0.05 的K-S 检验,即假设的边缘分布合理。
3.1.2 联合分布
利用Gumbel-Hougaard、Frank、Clayton、Ali-Mikhail-Haq Copula 分别建立二元联合模型,按照边际函数推断法计算得到联合分布模型参数,并相应计算BIC 统计量,结果见表3。按照指标最小值对应的即为最优模型准则,Frank Copula 即为最佳联合模型。

表3 二元Copula 联合分布模型参数计算结果表
通过CPI Rosenblatt 转换检验法对Fank Copula拟合效果进行检验,统计量取A—D,样本的检验统计值An2 为0.446 4,小于显著性水平α=0.05 时的临界值=0.604 2,满足An检验要求,即二元Frank Copula 联合分布是合理的。拟合的联合分布见图1。
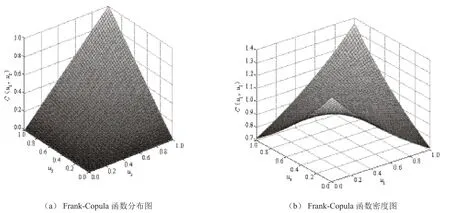
图1 建立的Frank-Copula 联合分布图
3.2 设计组合风险分析
由式(6)分别计算出重现期为2~100 a 的高潮位和同期不同重现期的潮差组合风险率,见表4。
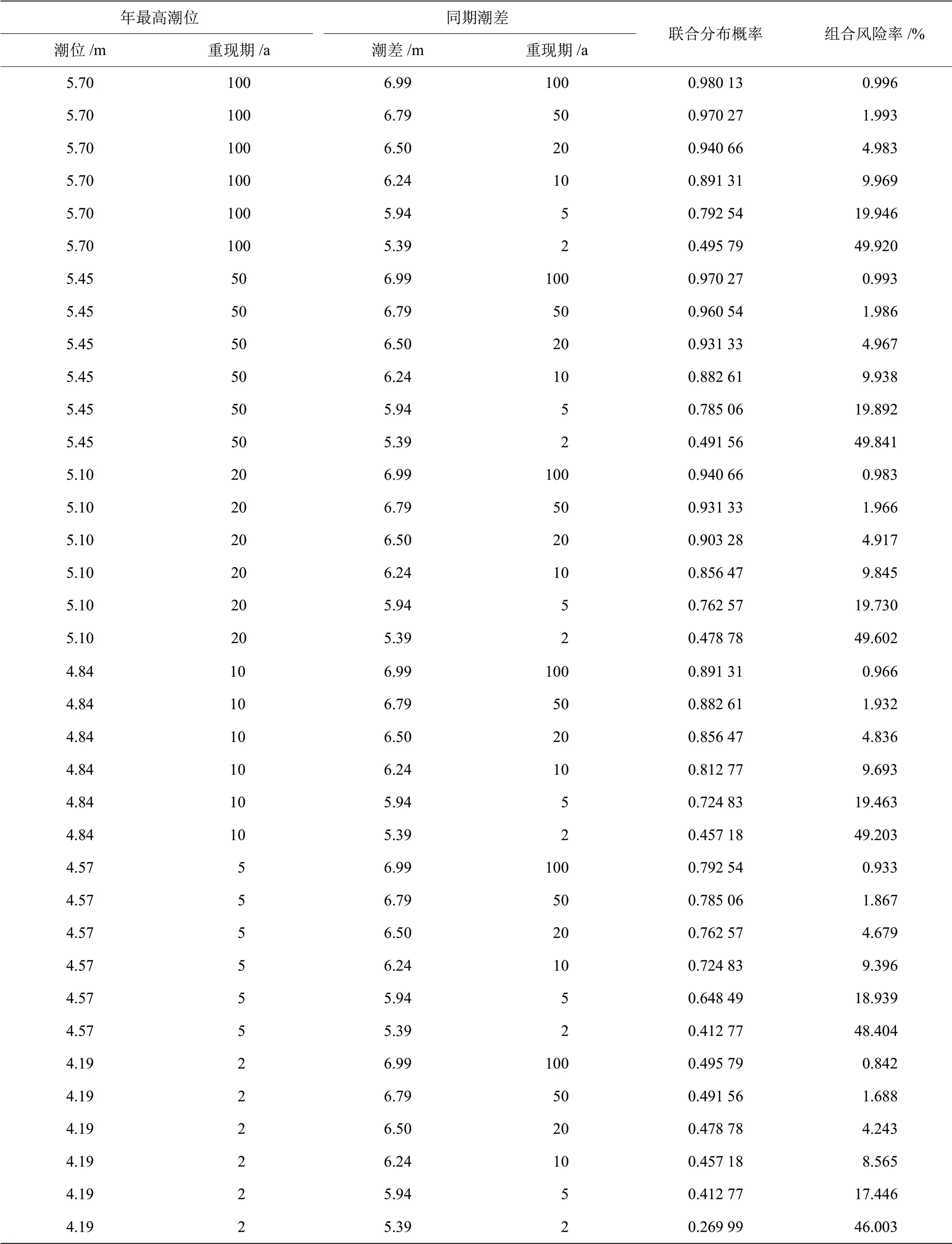
表4 设计高潮位与同期潮差组合风险率表
由表4 可知,温州站高重现期高潮位,遭遇高重现期潮差的组合风险值较低,遭遇可能性较小,随着遭遇潮差的重现期减小,遭遇组合风险值逐渐变大,遭遇可能性变大;同一重现期的潮差,遭遇高潮位的重现期变小,组合风险率变小,但变化不大。总体上,温州站设计高潮位与潮差不具备同频性,不同重现期的高潮位遭遇低重现期潮差的概率更高,也就是说高潮位与低潮差的组合出现概率更高。
3.3 条件最可能组合及设计潮位过程线
实际防洪(潮)排涝设计中,对安全影响更大的因素是高潮位,所以潮位过程线的设计考虑以高潮位设计为主,同时考虑在给定高潮位条件下,出现几率最大的潮差。根据式(5),利用遗传算法计算给定重现期的设计高潮位下的条件最可能潮差,计算结果见表5。
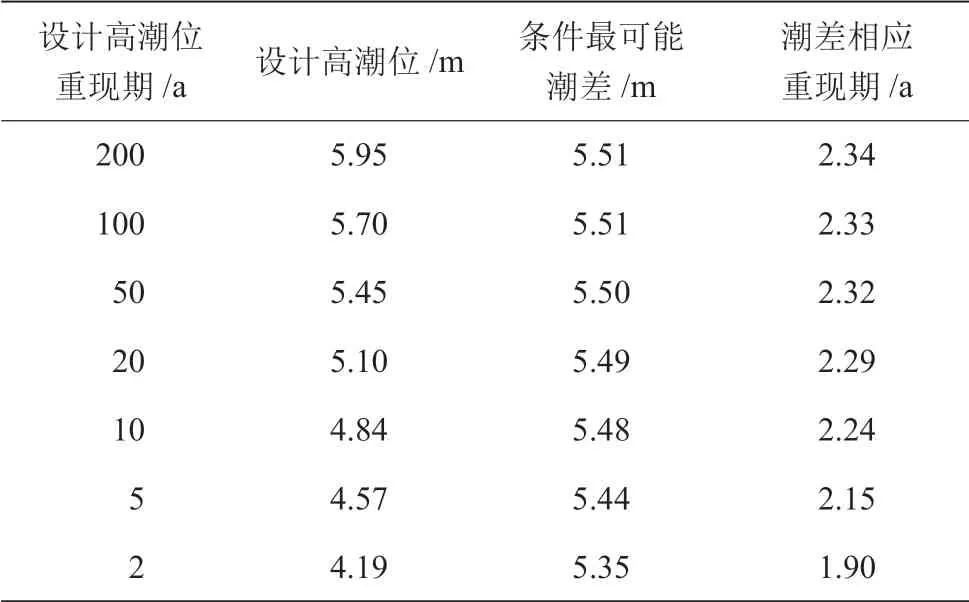
表5 设计高潮位及条件最可能潮差计算结果表
由表5 可知,温州站重现期为2~200 a 的设计高潮位下,条件最可能发生的潮差为1.90~2.34 a一遇,也就是说不同重现期的设计高潮位最可能遭遇的是低重现期的潮差。分析原因,主要是发生高重现期的潮水过程中,高潮位变大,事实上此时整个潮位抬升,风浪爬高,所以低潮位也会相应抬升,因此潮差不会加剧反而相对维持一个较小值。
由求出的设计高潮位与条件最可能潮差组合,按照双重控制,缩放典型潮型即可得到设计潮位过程线。为比较不同方法的差异,将本文所用方法与仅设计高潮位控制、同频率法等方法所推求的设计潮位过程线绘于同一图(见图2)。
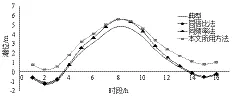
图2 不同方法推求的设计潮位过程线图
由图2 可见,几种方法的设计高潮位相同,但是同频率设计方法推求的设计潮位过程线的低潮位更低,不一定能反映真实的风暴增水过程。而采用本文方法推求的设计潮差是在考虑年最高潮位和同期潮位相关性的基础上,根据实测资料拟合确定,数据统计基础更强,在防洪排涝规划与设计中,更不利于排涝,用于计算安全裕度更大,对于以考虑高潮位为主的防潮排涝工程设计而言更具合理性,有一定参考意义。
4 结 论
(1)采用Frank Copula 函数构建瓯江温州站年最高潮位和同期潮差二元联合分布合理可行。
(2)从概率统计上分析,瓯江高潮位与潮差不具备同频率的特性;高重现期的设计高潮位与低重现期的潮差组合概率风险更大,遭遇可能性更高。
(3)基于联合分布,构造给定重现期的设计高潮位下最可能的潮差模型,首次尝试用遗传算法求解该模型,结果证明遗传算法有效,利用设计高潮位与条件最可能潮差组合推求潮位过程线的方法可行。该方法统计理论依据充分,较同频率法更合理,且该方法设计低潮位较同频率法更高,潮位过程偏不利,用于防洪排涝工程设计计算安全裕度更大。

