基于三台阶开挖工法的锁脚锚杆位置模拟优化

燕 新，焦云成，高明明，彭 浩

(1. 新疆维吾尔自治区交通规划勘察设计研究院，乌鲁木齐 830006； 2. 广西路桥工程集团有限公司，南宁 530200)

随着我国道路网的不断规划，隧道工程项目越来越多，在隧道施工过程中遇到的问题也逐渐增多[1-2]，如坍塌冒顶、大变形以及突泥涌水等问题。在软岩隧道修建中，如何发挥支护结构的有效性并保证隧道施工的安全性，一直是相关科研技术人员研究的难点。

软岩具有明显的蠕变性质[3-4]，对围岩和支护结构的稳定性具有显著影响。国内外学者对软岩工程性质的影响开展了大量研究，李永盛[5]和许宏发[6]对不同岩石开展蠕变试验，分别给出了岩石的蠕变规律和深入研究方向。Yamatomi[7]提出岩石强度与应变速率之间的关系，同时也指出用黏弹性本构模型来描述岩石的蠕变变形和蠕变破坏。根据围岩的力学特性，Park等[8]利用图解法阐述收敛法的基本概念，并绘制了支护特征曲线。Brown等[9]在1983年基于Hoek-Brown(霍克-布朗)屈服准则等给出围岩应力释放过程曲线与支护措施的反应曲线。根据围岩的应力释放过程和结构受力过程，学者们提出了不同处置措施，如双层支护[10-11]、三层支护[12]以及锁脚锚杆[13]等方法。对于锁脚锚杆的研究，陈建勋等[14]采用试验方法，验证了锁脚锚杆在软岩隧道中的支护效果。在此基础上，陈丽俊等[15]和罗彦斌等[16]给出不同锁脚锚杆的计算模型，但对于锁脚锚杆施作的位置研究较少，本文基于新疆乌尉1号软岩隧道，采用数值模拟软件MIDAS GTS对三台阶开挖工法下的锁脚锚杆施作位置进行分析。

1 支护等效

1.1 锁脚锚杆的作用

锁脚锚杆一般布置在台阶开挖处，主要作用为：①锁住钢拱架的端部，增加钢拱架与围岩的接触，充分承担围岩的形变压力，约束钢拱架的纵向和竖向变形；②发挥锚杆的锲固和挤压作用，提高台阶周边围岩的物理力学参数值，充分发挥围岩拱形的自承载能力。

1.2 支护结构等效

为精确模拟锁脚锚杆的作用和优化三台阶施工工法下锁脚锚杆施作的位置，采用控制变量法对锁脚锚杆进行模拟。首先对系统锚杆加固区域的参数进行等效，假设岩体和锚杆组成的复合体服从Mohr-Coulomb(摩尔-库伦)屈服准则，支护前后围岩的屈服准则大小如图1所示。

由文献[17]可知，系统锚杆与围岩形成的复合体黏聚力c*、内摩擦角φ*、弹性模量E*以及隧道的等效圆半径a的表达式如式(1)～式(4)所示。

(1)

(2)

(3)

(4)

式中，φ*为围岩的内摩擦角，c*为围岩的黏聚力，Eb为锚杆的弹性模量，a为隧道的等效圆半径，sr为锚杆环向间距，sl为隧洞轴向锚杆排距，rb为锚杆半径，E*为岩体弹性模量，R1、R2、…、Rn为隧道轮廓线的半径，n为隧道圆心数量。

2 工程简介

以新疆乌尉1号软岩隧道为研究背景，该隧道设计为分离式单洞长隧道，单洞断面尺寸净高为5.00 m，净宽为18.25 m，隧道横断面如图2所示。现场地质调绘发现该隧址区K33+90前后、K34+200前后、K34+350、K35+02前后、K35+700～800前后及K36+400前后，发育6条规模较大的横向挤压破碎带，破碎带内为碎石土、块石以及破碎岩体等，冲沟侧壁基岩挠曲破碎，其中K35+020及K36+400冲沟均见有孔隙水和裂隙水出露。

新疆乌尉1号软岩隧道以强-中风化凝灰质砂岩为主，石炭系块状凝灰质砂岩如图3所示，岩体基本质量指标(BQ)为164.4，属较软岩，岩体完整性较差，结构面发育，结合较差，岩体破碎，呈薄层状、片状结构，少量裂隙水。在开挖时围岩易失稳、支护结构易被破坏，分析原因可知，该支护结构局部刚度过小，造成整体支护失稳。本次主要针对乌尉隧道1号软岩隧道Ⅴ级断面进行锁脚锚杆优化。

3 数值模拟

3.1 模拟参数

本次围岩参数选取Ⅴ级ZK33+330断面，岩体基本质量指标(BQ)为164.4，单轴饱和抗压强度为12 MPa，属于软岩。

计算参数为：重度=27.4 kN/m3，变形模量Es=2 GPa，泊松比=0.176，内摩擦角=39.92°，黏聚力=3.49 MPa。

系统锚杆参数为：系统锚杆采用Φ42×4 mm注浆钢花管，锚杆半径rb=21 mm，锚杆环向间距sr=11 cm，轴向锚杆排距sl=0.6 m，弹性模量Eb=206 GPa，隧道圆心数量n=3。

其他参数为：钢拱架采用I22b工字钢；采用C25喷射混凝土。

3.2 工况设定

工程采用三台阶开挖工法，锚杆锁脚位置示意如图4所示，图中β为锁脚锚杆与水平面的夹角。原锁脚锚杆仅设计于C和C1处，在原设计基础上，本次探究锁脚锚杆施作位置对凝灰质砂岩隧道变形的约束作用。

锁脚锚杆位置工况设定如表1所示，其中锁脚锚杆长度为4 m，插入角度为12°。

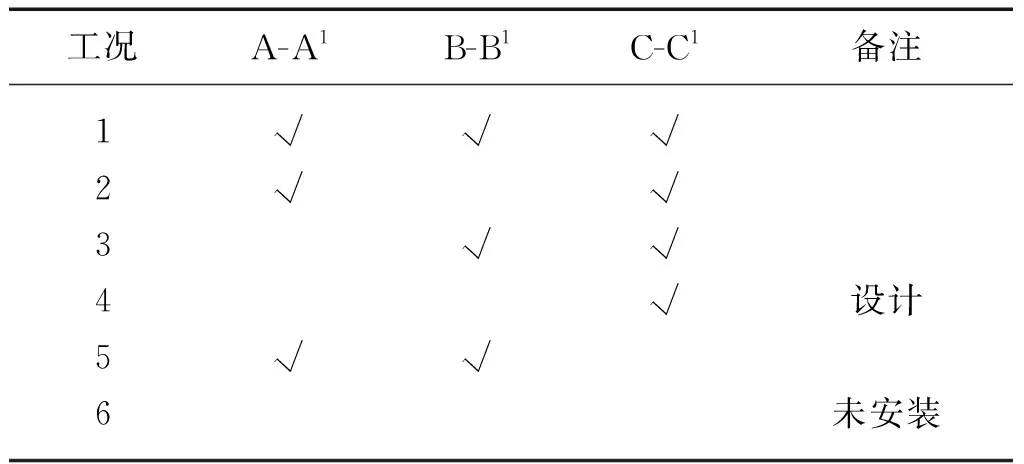
表1 锁脚锚杆位置工况设定

3.3 模型建立

由于新疆乌尉1号软岩隧道长度远大于隧道断面距离，简化三维模型为二维模型，采用MIDAS GTS软件建立依托工程二维模型。模型长度×宽度为200 m×500 m，二维隧道模型如图5所示。模型边界条件：x=-100时，位移为0；x=100时，位移为0；y=-200时，位移为0。

为分析锁脚锚杆施作位置对围岩拱顶变形和周边收敛约束的效果，本次布置5个测点和3条测线进行监测。测点及测线布置示意如图6所示。

3.4 变形分析

3.4.1 拱顶竖向最大位移

工况1拱顶位移云图如图7所示，不同工况下y方向位移曲线如图8所示。

工况1和工况3对比，上台阶施作锁脚锚杆后，拱顶最大沉降值为20.2 mm，上台阶未施作锁脚锚杆，拱顶最大沉降值为32.4 mm，沉降值增加了60.4%。工况1和工况2对比，中台阶施作锚杆后，拱顶累计沉降值为31.5 mm；中台阶未施作锚杆，拱顶累计沉降值为33.5 mm，拱顶累计沉降值增加了6%。工况1和工况5对比，下台阶拱脚处施作锁脚锚杆，拱顶累计变形量为45.6 mm，下台阶未施作锁脚锚杆，拱顶累计变形量为65.6 mm，变形量增加了43.9%。

对比分析可知，上台阶和拱脚处施作锁脚锚杆对围岩拱顶变形有明显抑制作用；中台阶处施作锁脚锚杆对拱顶的控制作用较小。由工况3和工况4对比可进一步说明上台阶开挖后施作锁脚锚杆对围岩变形有明显约束作用。

3.4.2 周边收敛

工况1周边收敛位移云图如图9所示。不同工况下测线b-b1的x方向位移曲线如图10所示。

工况1和工况2对比，随着隧道开挖工序的进行，中台阶施作锁脚锚杆时b-b1测线的周边变形值分别为17.6 mm和19.4 mm，未施作锁脚锚杆时收敛值分别为20.6 mm和22.5 mm，周边收敛值分别增加了17%和15.9%。工况1和工况3对比，上台阶未施作锁脚锚杆时b-b1测线的周边变形值分别为18.9 mm和21.7 mm，收敛值增加了7.4%和9.8%。由工况1、工况2、工况3和工况4对比可知，上台阶施作的锁脚锚杆对b-b1测线的周边收敛控制效果较小。对比工况1和工况5，下台阶处未施作锁脚锚杆时b-b1测线的周边收敛值为22.6 mm，相比工况1增加了16.5%。

分析可知中台阶的锚杆施作和下台阶处的锚杆施作对b-b1测线的周边变形有明显控制作用，上台阶处施作锁脚锚杆对b-b1测线的周边变形控制效果降低。不同工况下测线c-c1的x方向位移曲线如图11所示。

由图11可知，工况1至工况6中c-c1测线的周边变形分别为23.4 mm、26.8 mm、24.9 mm、25.7 mm、25.5 mm和29.5 mm，分析表明中台阶处施作锁脚锚杆对c-c1有着明显的控制作用。

分析原因可知，上台阶围岩开挖扰动后，岩体内部的能量瞬时释放，围岩产生大变形，因此上台阶的支护结构和支护方式对围岩变形起重要作用。锁脚锚杆添加上台阶钢拱架与围岩的黏附力，增加开挖区域钢拱架的环向抗力，同时发挥锚杆的悬臂梁作用，提升扰动围岩的整体性，从而抑制围岩变形。

上台阶开挖后，隧道变形能量已经得到一定程度释放，同时上台阶施作锁脚锚杆抑制着上部围岩的变形，中台阶开挖处发挥较小作用。随着隧道开挖应力的改变，围岩边墙处的切向剪应力增大，边墙向内挤出，中台阶处施作锁脚锚杆约束钢拱架横向脱离，抑制围岩周边变形。

随着下台阶和仰拱的开挖，仰拱未施作前，初期支护未闭合成环，拱脚受力复杂，围岩变形大，拱脚处施作锁脚锚杆实现隧道断面的成环效应，减少隧道变形。

进一步分析可知，工况1拱顶沉降和周边收敛最小，工况6隧道拱顶沉降和收敛最大，同时与其他工况对比可知锁脚锚杆对新疆乌尉1号软岩隧道变形有一定控制作用。

4 结论

基于新疆乌尉1号软岩隧道锁脚锚杆设计理念，采用MIDAS GTS数值模拟软岩，分析锁脚锚杆的施作位置对围岩变形的影响。以乌尉1号软岩隧道施工方法为基础，探究锁脚锚杆施作上中下台阶处对围岩变形效果的影响。根据模拟结果可知，上中台阶处施作锁脚锚杆对围岩拱顶变形有明显约束作用；中台阶和下台阶处施作锚杆对围岩周边收敛有明显作用。

基于乌尉1号软岩隧道锁脚锚杆设计参数，仅对施作锚杆的位置进行优化验证，并未验证锁脚锚杆的长度和角度，因此还应进一步研究锁脚锚杆的长度和角度对位置的影响。