2021 年江苏省数学中考优秀题例

优秀试题一

【原题呈现】

（2021 年盐城卷）3.北京2022年冬奥会会徽如图1 所示，组成会徽的四个图案中是轴对称图形的是（）

（图1）

（2021 年徐州卷）8.如图2，一枚圆形古钱币的中间是一个正方形孔，已知圆的直径与正方形的对角线之比为3∶1，则圆的面积约为正方形面积的（）

A.27倍 B.14倍 C.9倍 D.3倍

【试题评析】

考查目标方面，两题分别考查了学生对轴对称图形的理解及对称图形性质的认识，要求学生能根据生活中的图案正确识别轴对称图形，利用对称图形的性质进行相关数量关系的认定，从而计算简单图形的面积。情境呈现了数学之美，渗透了中国现代与古代的文化。

素养导向方面，两题蕴含了对学生直观想象素养的考查，要求学生对图案的对称性作出直观判断，并根据圆与正方形的对称属性抽象出基本图形的数量关系。

（图2）

教学建议方面，教学中要结合时代特色和中国文化，选择能引发学生兴趣、激发学生思考的情境，引导学生用数学的眼光去思考问题，用数学的方法去研究问题，体现数学的实际应用价值。

优秀试题二

【原题呈现】（2021年南京卷）

21.某市在实施居民用水定额管理前，对居民生活用水情况进行了调查。通过简单随机抽样，获得了100 个家庭去年的月均用水量数据，将这组数据按从小到大的顺序排列，其中部分数据如下表：

序号月均用水量/t 1 2 1.3 1.3……25 4.5 26 4.5……50 6.4 51 6.8……75 11 76 13……99 25.6 100 28

（1）求这组数据的中位数。已知这组数据的平均数为9.2t，你对它与中位数的差异有什么看法？

（2）为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5 倍价格收费。若要使75%的家庭水费支出不受影响，你觉得这个标准应该定为多少？

【试题评析】

考查目标方面，本题考查了学生对中位数和平均数概念的理解，以及如何利用数据分析结果作出决断。本题情境是生活中真实的场景，没有设置烦琐的计算，注重考查学生对统计量的理解，使学生感悟统计量的本质内涵。

素养导向方面，本题蕴含了对学生数据分析素养的考查，答案较为开放，意在考查学生数据分析的意识与能力；要求学生将内在信息相联系，从中看出关联性，考查学生用数学的眼光和思维分析现实世界的能力，体现了数据分析的基本思想方法。

教学建议方面，统计教学的有效方法是让学生亲身经历数据收集、整理、分析的全过程，教师可创设学生身边的真实情境，在教学活动中让学生形成读懂数据的意识，掌握数据的分析方法，并能用数据分析的结果进行合理决策与判断。

优秀试题三

【原题呈现】（2021年连云港卷）

6.关于某个函数表达式，甲、乙、丙三位同学都正确地说出了该函数的一个特征。甲：函数图象经过点（-1，1）。乙：函数图象经过第四象限。丙：当x＞0 时，y随x的增大而增大。则这个函数表达式可能是（）

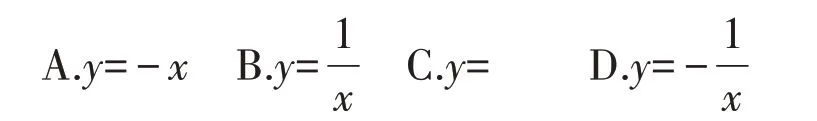
【试题评析】

考查目标方面，本题考查了学生对正比例函数、反比例函数及简单的二次函数的理解，要求学生在充分掌握三种函数图象与性质的相关知识下进行解答。

素养导向方面，本题蕴含了对学生数学抽象素养的考查，要求学生能用数学符号语言（函数表达式）准确描述数学对象，将碎片化的信息抽象成数学对象，有利于学生数学抽象素养的养成。

教学建议方面，数学抽象一般要经历寻找属性、特征概括、数学表达、纳入系统的过程。教学中，要注重让学生学习不同函数的共同主线，结合数形理清函数学习的线索，形成知识的网格；合理设计抽象活动，引导学生从数学概念的生成过程中抽象出数学结论。

优秀试题四

【原题呈现】（2021年盐城卷）

21.如图，点A是数轴上表示实数a的点。

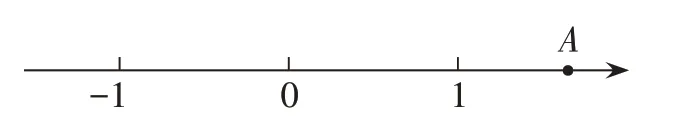
【试题评析】

考查目标方面，考查了学生对尺规作图、实数与数轴上点一一对应关系、实数的大小比较等知识的掌握程度，要求学生在掌握尺规作图的方法及在理解无理数概念的基础上进行解答。

素养导向方面，本题蕴含了对学生数学抽象素养的考查，要求学生能够识别复杂情境中的数学概念，根据 2 的意义与图形表达间的联系，借助数轴进行实数大小的直观比较。

教学建议方面，数学抽象应贯穿于课堂教学的全过程，教学中要以某一抽象活动为主线，让学生感知无理数出现的必然性与必要性。教学中要合理采用不同的抽象方法，如基于概念的抽象、基于规则的抽象、基于方法的抽象等。

优秀试题五

【原题呈现】（2021年镇江卷）

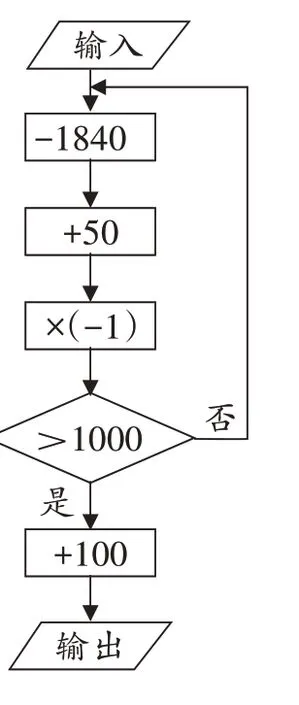
16.如图，输入数值1921，按所示的程序运算（完成一个方框内的运算后，把结果输入下一个方框继续进行运算），输出的结果为（）

A.1840 B.1921 C.1949 D.2021

【试题评析】

考查目标方面，本题以数值转换器为依托，考查了学生对有理数混合运算及算理算法理解的掌握情况，要求学生能根据程序列出算式，并进行正确的运算和判断。

素养导向方面，本题蕴含了对学生数学运算素养的考查，要求学生能够正确理解程序的表述，正确、迅速完成运算。在解题的过程中，学生要经历分析运算对象、尝试运算方向、选择运算规则、计算并判断结果等环节，体现出数学运算也是数学思考的重要方式。

教学建议方面，正确、灵活、合理、简洁是衡量学生数学运算素养的四个特征，教学中教师要结合具体情境，帮助学生理解“为什么这样算”和“怎样算”，要重视引导学生经历运算法则的生成过程，让学生感受法则的合理性。帮助学生理解算理、掌握算法是教学的关键。

优秀试题六

【原题呈现】（2021年泰州卷）

23.（1）如图①，O为AB的中点，直线l1、l2分别经过点O、B，且l1//l2。以点O为圆心，OA长为半径画弧交直线l2于点C，连接AC。求证：直线l1垂直平分AC。

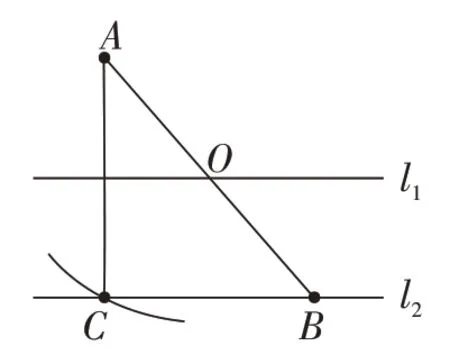
（图①）

（2）如图②，平面内直线l1//l2//l3//l4，且相邻两直线间距离相等，点P、Q分别在直线l1、l4上，连接PQ。用圆规和无刻度的直尺在直线l4上求作一点D，使线段PD最短。（两种工具分别只限使用一次，并保留作图痕迹）

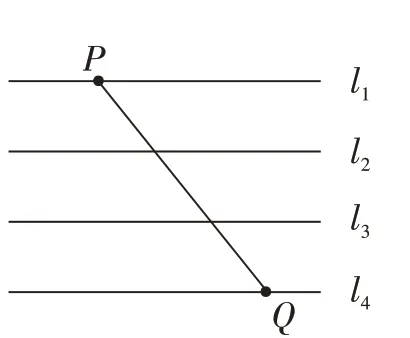
（图②）

【试题评析】

考查目标方面，解决本题所运用的知识有等腰三角形三线合一、一条直线垂直于平行线中的一条则必然垂直于另一条直线等，都是学生必须理解与掌握的基本定理。

素养导向方面，本题将几何推理与尺规作图有机结合，具有源于教材、方法迁移、几何推理等特点，突出考查了逻辑推理的核心素养。

教学建议方面，本题设计精巧，两个小问之间存在递进关系，第一问考查基础知识与基本方法，其图形结构、作图与证明方法为第二问的探究积累了活动经验，提供了探究思路。本题的图形及结论在教材中有多处原型，充分挖掘和利用教材资源命制试题，可引导教师重视教材在教学中的作用。

优秀试题七

【原题呈现】（2021年苏州卷）

18.如图，射线OM、ON互相垂直，OA=8，点B位于射线OM的上方，且在线段OA的垂直平分线l上，连接AB，AB=5。将线段AB绕点O按逆时针方向旋转得到对应线段A′B′，若点B′恰好落在射线ON上，则点A′到射线ON的距离d=____。

【试题评析】

考查目标方面，本题以图形的旋转为设问背景，考查了勾股定理、相似三角形、锐角三角函数等知识点，不同的学生有不同的解法，思维深刻的学生运算量很小，是一道体现“少算深思”的好题。

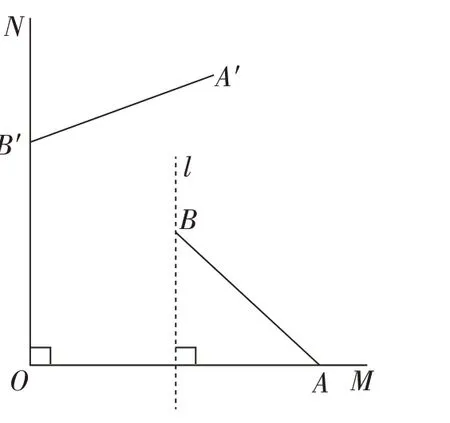
素养导向方面，本题在分析构图的基础上需要考生有较强的逻辑推理能力，能根据条件推导出旋转前后哪些对应线段或角是相等的。

教学建议方面，作为一道填空题的较难题，本题较好地体现了区分选拔功能，教学时教师可安排学生交流不同的解法，然后让学生在对比中找到更好的解法，积累解题经验，感悟旋转变换中的“变与不变”。

优秀试题八

【原题呈现】（2021年扬州卷）

28.甲、乙两汽车出租公司均有50 辆汽车对外出租，下面是两公司经理的一段对话。

甲公司经理：如果我公司每辆汽车月租费3000 元，那么50 辆汽车可以全部租出；如果每辆汽车的月租费每增加50 元，那么将少租出1辆汽车；另外，公司为每辆租出的汽车支付月维护费200元。

乙公司经理：我公司每辆汽车月租费3500元，无论是否租出汽车，公司均需一次性支付月维护费共计1850元。

说明：①汽车数量为整数；②月利润=月租车费-月维护费；③两公司月利润差=月利润较高公司的利润-月利润较低公司的利润。

在两公司租出的汽车数量相等的条件下，根据上述信息，解决下列问题：

（1）当每个公司租出的汽车为10 辆时，甲公司的月利润是____元；当每个公司租出的汽车为____辆时，两公司的月利润相等。

（2）求两公司月利润差的最大值。

（3）甲公司热心公益事业，每租出1 辆汽车捐出a元（a＞0）给慈善机构，如果捐款后甲公司剩余的月利润仍高于乙公司月利润，且当两公司租出的汽车均为17 辆时，甲公司剩余的月利润与乙公司月利润之差最大，求a的取值范围。

【试题评析】

考查目标方面，本题综合考查一元二次方程、一次函数、二次函数等初中代数核心知识。

素养导向方面，数学核心素养要求学生会用数学的语言表达现实世界，在现实生活中构建普适的数学模型，形成合理的判断和决策，这道考题主要考查的是分析生活情境、选取数学模型（方程、函数）进行判断和决策的能力。

教学建议方面，教学时教师要让学生对现实生活问题充分审题与分析，恰当设出未知数、分析不同未知量之间的数量关系是列出方程或函数关系式的关键。此外，如果构建函数解决实际问题，还应特别注意自变量的取值范围。

优秀试题九

【原题呈现】（2021年南通卷）

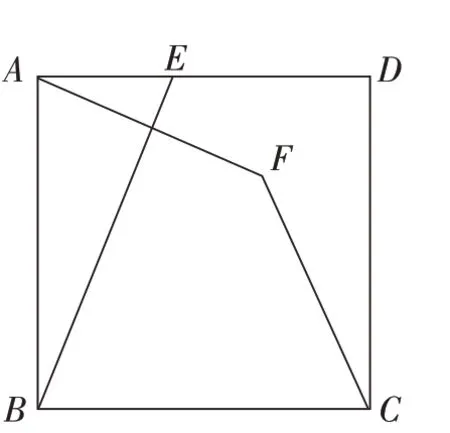
25.如图，正方形ABCD中，点E在边AD上（不与端点A、D重合），点A关于直线BE的对称点为点F，连接CF，设∠ABE=α。

（1）求∠BCF的大小（用含α的式子表示）。

（2）过点C作CG⊥直线AF，垂足为G，连接DG。判断DG与CF的位置关系，并说明理由。

（3）将△ABE绕点B顺时针旋转90°得到△CBH，点E的对应点为点H，连接BF、HF。当△BFH为等腰三角形时，求sinα的值。

【试题评析】

考查目标方面，本题综合考查了翻折、旋转、锐角三角函数等知识点，是一道几何综合题。

素养导向方面，本题以正方形为问题背景，从轴对称出发，渐次探究角度、直线位置关系，最后安排学生探究旋转变换后的等腰三角形的存在性问题，有效地考查了学生的几何直观、逻辑推理等数学素养。

教学建议方面，本题的亮点是解法多样，比如前两问，学生可以运用八年级的知识与技能解答，也可利用“四点共圆”获得简洁的解法，体现了针对经典问题的深刻理解和初等方法的求解追求。教师在开展该题的解题教学时可以引导学生进行解法展示与对比分析。

优秀试题十

【原题呈现】（2021年常州卷）

26.【阅读】通过构造恰当的图形，可以对线段长度、图形面积大小等进行比较，直观地得到一些不等关系或最值，这是“数形结合”思想的典型应用。

【理解】（1）如图①，AC⊥BC，CD⊥AB，垂足分别为C、D，E是AB的中点，连接CE。已知AD=a，BD=b（0＜a＜b）。

①分别求线段CE、CD的长（用含a、b的代数式表示）；

②比较大小：CE____CD（填“＜”、“=”或“＞”），并用含a、b的代数式表示该大小关系。

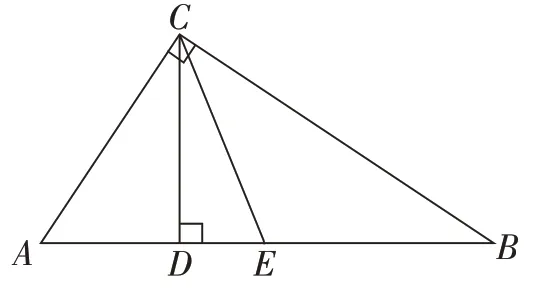
（图①）

（图②）

①当m=1，n=2 时，l=____；当m=3，n=3 时，l=____；

②通过归纳猜想，可得l的最小值是____。请利用图②构造恰当的图形，并说明你的猜想成立。

【试题评析】

考查目标方面，本题主要考查了垂线最短、勾股定理、反比例函数、数式变形与化简等关键能力。本题构思精巧，融“数、形”于一体，是一道华罗庚先生所说的“数缺形时少直观”的好题。

素养导向方面，本题以“数形结合”作为鲜明的命题主线，两个问题串由易及难、渐次生长，突出了对直观想象素养的考查。第一问先给出学生熟悉的基本图形，让学生简要运算比较、确认“垂线段最短”；第二问从特殊到一般，让学生先猜想结论，再构图验证。

教学建议方面，这道试题彰显了数学中的“合情猜想—构图验证”的研究方法。教学中，教师要重视对基本图形及其性质的研究路径的引导；要注重培养学生从特殊到一般、类比转化、数形结合等数学基本思想方法。