发电厂用蓄电池在线监视与寿命预测

孔令伟，郭权利，张思博，周玉玲，刘 冬

（1.沈阳工程学院 电力学院，辽宁 沈阳 110136；2.吉林电力股份有限公司二道江发电公司，吉林 通化 134000）

UPS（Uninterruptable Power Supply）电源系统可以保证发电厂供电不间断，是安全运行的保障。阀控式铅酸（VRLA，Valve Regulated Lead Acid）蓄电池作为电源系统的储能设备是发电厂中直流电源系统的核心，其好坏直接决定供电系统停电后能否不间断供电。典型的UPS 后备电源应用如图1所示，UPS电源系统一般由VRLA蓄电池串联成电池组进行供电［1-3］。

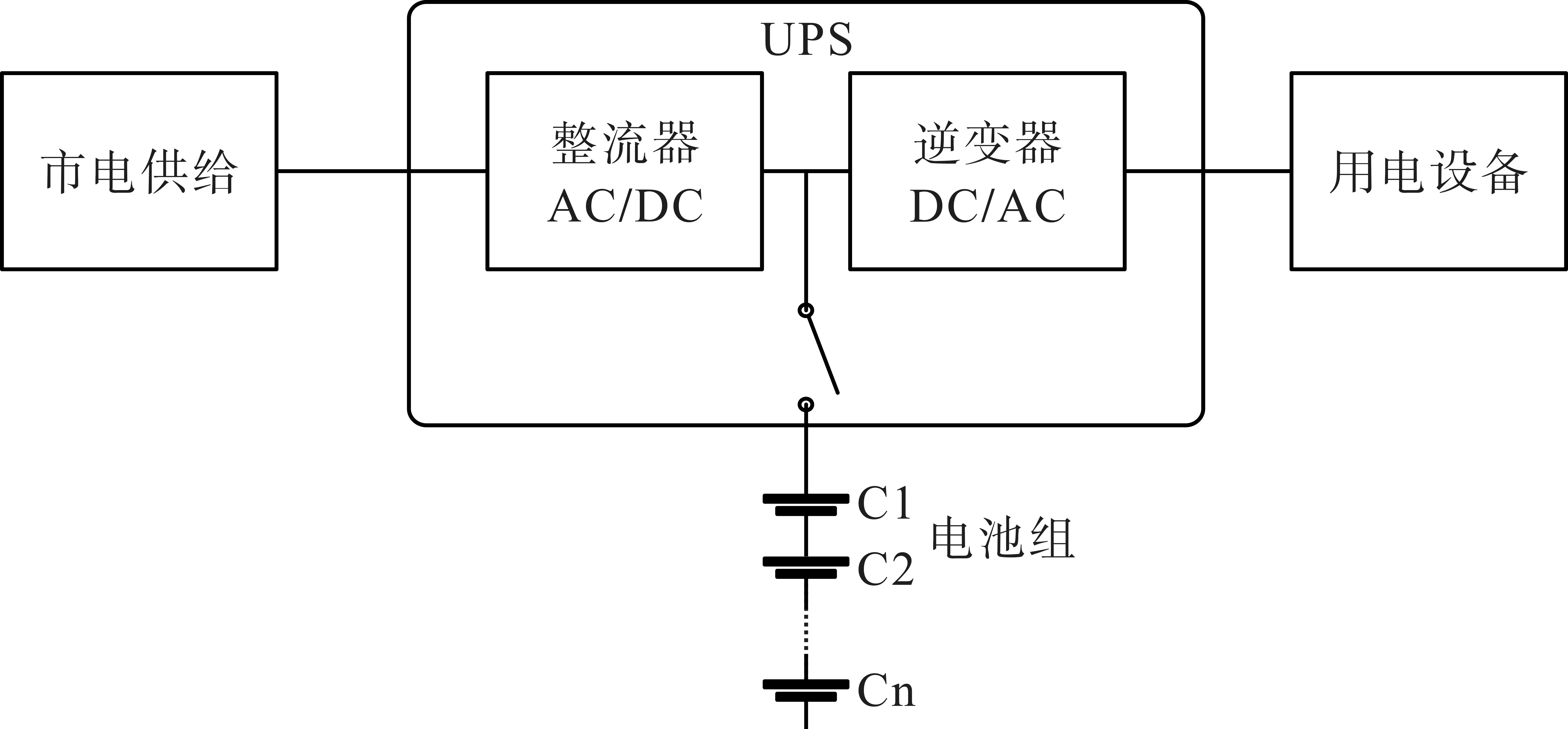
图1 典型的UPS后备电源应用

蓄电池组的安全稳定直接影响整个系统的正常运行，错误操作或未定期维护都会减少蓄电池组的使用寿命，甚至导致个别电池失效。因蓄电池串联工作，所以当个别电池失效时会对其他蓄电池产生影响，造成巨大经济损失。在UPS 电源系统故障中，与蓄电池有关的故障占30%以上。蓄电池投入运行后因短期内不会更换，故需要加强对蓄电池的性能指标的监测。监测蓄电池的性能指标在一定程度上会反映蓄电池的实际工作状态，以此作为依据对其使用寿命进行预测，保证了UPS 电源的稳定运行，也能减少不必要的经济损失。抚顺发电厂2号机曾在启动给水泵时发生UPS电源中断，造成DCS 系统及工业监视器电源消失，机组失去远方监视和控制手段，运行人员立即就地打闸停机，对机组造成极大影响。

1 影响VRLA蓄电池寿命的因素

1.1 容量

阀控式铅酸蓄电池发出的电量表示其容量，电池容量常用C来表示。蓄电池由于长期处于完全放电或半放电状态以及负极板硫酸化等，会导致蓄电池容量减小［4-5］。

1.2 电压

VRLA 蓄电池电压是由组成蓄电池的各个单元的单位电压串联得到的，故电压等于各单位电压之和。在蓄电池工作运行过程中，不同阶段对蓄电池运行产生影响的电压也不同［6-7］，如开路电压、浮充电压、放电终止电压等。

1.3 内阻

VRLA 蓄电池的内阻是指电流通过电池时所受到的阻力，电池内部结构不同直接影响内阻值的大小［8-9］。

1.4 其他因素

除上述的影响阀控式铅酸蓄电池寿命的因素以外，还包括放电时率、放电倍率、温度等。这些影响因素都可以间接通过以上3 点因素反映出来，而且阀控式铅酸蓄电池电化学反应复杂，可能引起故障的原因过多。除了电池本身还包括外部因素，例如安装不当、工作人员操作失误等。

2 VRLA蓄电池监测技术的研究现状

2.1 VRLA蓄电池容量监测

1）离线容量测试

放电试验是测试电池容量最直接准确的方法，可以迅速查出电池与外电路之间的故障。但缺点同样明显：离线测试需要电池脱离工作状态，在整个试验期间，电池失去了当发生故障时为系统供电的作用，不能保证供电的连续性；同时，放电试验也会减少电池的寿命，不利于电池的维护和保养。

2）模糊逻辑推理和神经网络方法

神经网络能通过已知信息进行自我学习，进而优化自身结构并实现自动控制。模糊逻辑可以参照人脑来分析判断，运用多值逻辑推理思维通过模糊集合来处理模糊关系，通过模拟人脑方式进行综合判断推理以解决信息问题。

但在实际运行中，蓄电池工作影响因素较多，用模糊逻辑和神经网路方法分析和解决蓄电池的容量问题，在建立模型方面难度较大，准确性有待提高［10］。

2.2 VRLA蓄电池电压监测

1）浮充电压监测

在测量电池电压前，需要对被测电池进行浮充处理，再测量其电压值。当电池电压在系统允许范围内时，说明电池工作状态正常；当电压无变化或未在系统允许范围内时，说明原电压未达到系统标准要求［11］，该电池存在故障，很可能已经失水过多，电解液浓度过高，这时需要更换电池。

该方法的缺点是电解液的氧化反应会直接影响浮充电压的大小，故在测量浮充电压时会发生偏移，影响监测结果。

2）放电电压监测

在监测电池放电时，通过计算压降速率来检测阀控式铅酸蓄电池是否存在故障［12］。故障电池电压的下降速度相比正常电池电压的下降速度要快，下降波动范围大。利用发电时压降速率的不同来判断电池有无故障，可以使结果准确，但不足之处在于试验过程必须放电，需从系统中取出电池后才能检查是否存在故障电池。但在检测过程中电池脱离系统不能正常进行供电，使供电系统存在安全隐患，失去了故障预测的意义。

2.3 VRLA蓄电池内阻监测

1）直流放电法

直流放电法是将放电载体连接到蓄电池两侧，通过测量电压的变化求内阻值［13］。直流放电法在实际操作时需要离线测试，同时需要大量准备时间；直流放电法所测得的数据误差大，准确度达不到10%。

2）交流信号法

交流信号法是在蓄电池的两端施加固定频率和振幅的交流电压，这样使得测试得到的交流电流与交流电压保持同相，通过交流计算公式求出蓄电池的内阻。

采用该方法测量蓄电池内阻的优点在于保证了电池内阻的准确度与实时性，但也存在着不足：例如需要规定施加的交流信号幅度及交流信号不能干扰电池正常工作等。

3 最小二乘支持向量机预测模型的建立

最小二乘支持向量机（least square SVM，LSSVM）是对标准向量机的改进，改变了约束条件，通过转化为线性方程组求解，降低了计算复杂性，提高了求解速度和精度［14］。一般在蓄电池寿命预测模型进行数据处理时，被测蓄电池中可能存在故障电池，这就导致模型预测精度不高。但最小二乘支持向量机在进行数据处理时，通过寻找最优超平面极大地削弱了故障电池的影响。同时，最小二乘支持向量机适合于小样本的学习环境。基于该方法建立蓄电池寿命预测模型可以化简运算方式，提高效率。

3.1 数据预处理

若训练样本集为(xi,yi),i∈N;x∈Rd,y∈R［15］。首先，用非线性映射φ(·)将样本的输入空间Rd映射到特征空间φ(x)=(φ(x1),φ(x2),…,φ(xn))；其次，构造最优决策函数：y(x)=a⋅x+b；最后，以结构风险最小化为原则确定模型参数ω、b。

最优决策函数为

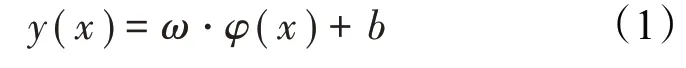
根据结构风险最小化原则，得到最小二乘支持向量机模型对应的Lagrange函数：

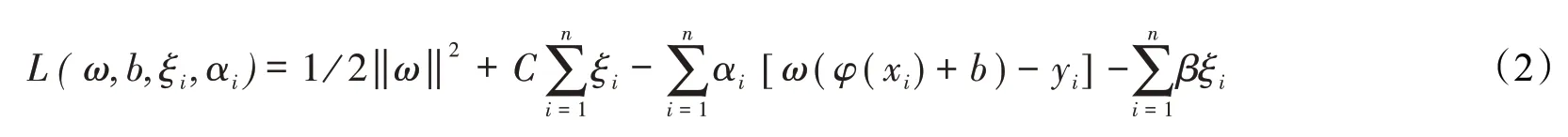
式中，αi=[α1,α2,…,αn]为Lagrange乘子。

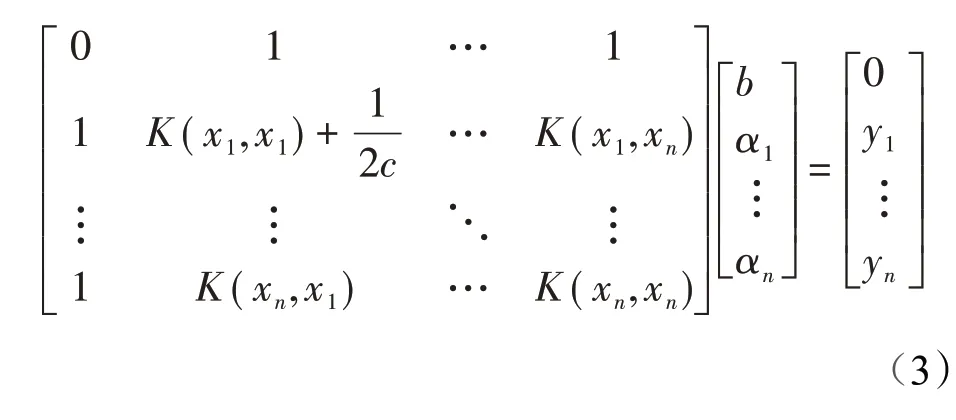
基于训练样本集(xi,yi)，可求解线性方程组，由最小二乘法计算b和αi，最后所确定的决策函数为

其中，支持向量系数α中不等于零的元素αi所对应的样本（xi，y）i称为支持向量。从决策函数式（4）可以看出，核函数K(x,xi)是输入向量从原始特征空间映射运算到高维特征空间，通过用已知的核函数来代替难以确定的高维映射函数，有效地解决了非线性问题。

3.2 核函数的选择

满足Mercer 条件的函数是核函数。不同的核函数构造不同的支持向量机模型，常见的核函数形式：

Sigmoid核函数表达式为

多项式核函数表达式为

径向基核函数（RBF）表达式为

构造基于Sigmoid 和RBF 的混合核函数，如下式：

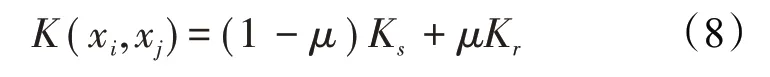
式中，0 ≤μ≤1。

针对文献［11］和文献［14］中核函数外推能力弱，建模运算量大，且运算精度不高等问题，本模型使用Sigmoid 和RBF 的混合核函数进行VRLA 蓄电池寿命预测，相较于单一核函数和其他混合核函数，其优点在于能解决非线性问题，并可以通过控制参数数量来实现预判，既提高了运算速度又提升了运算精度，是对最小二乘支持向量机的改进。

基于该核函数的决策函数为

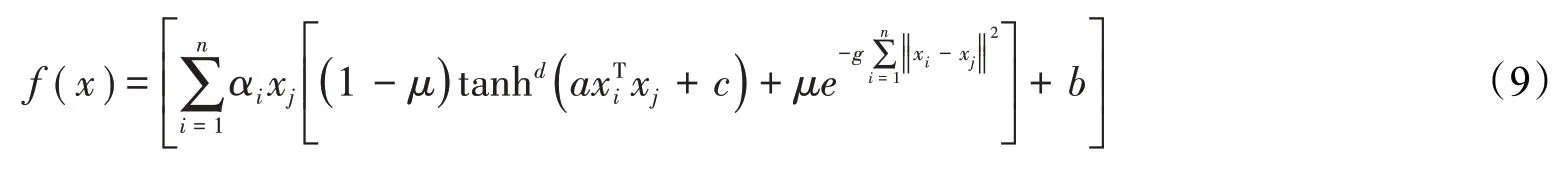
式中，xi为电压；xj为电池物理性能状态；a、b、c、d、g为待优化变量；αi为电流；μ为权重系数。

使用粒子群优化算法通过跟踪参数极值进行参数迭代。在粒子群优化算法中，平均误差函数应当能够反映出不同参数下LS-SVM 的泛化能力，平均误差公式为

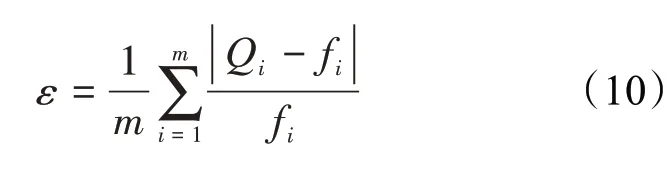
式中，Qi为第i点实际的测量值；fi为第i点预测值；m为验证样本数目。

3.3 实验方法与LS-SVM模型的建立

预测蓄电池的寿命最重要的因素是研究电解液密度，电解液密度的大小可以直观反映蓄电池的使用情况。因此，理论上可以通过测量蓄电池的端电压来预测蓄电池的使用寿命。但在实际使用过程中，随着蓄电池的老化，测量的端电压的变化已经不足以说明蓄电池的工作状态，故结合电池的SOH和端电压对蓄电池剩余电量进行预测，对提高预测的可靠性及精确性有重要意义。SOH用于描述电池物理性能的状态。故本文以蓄电池的端电压和电池的SOH为特征参数，确定模型的输入量与输出量。

以电池的SOH和电池的端电压作为输入量，建立LS-SVM 模型，预测蓄电池的使用寿命。蓄电池寿命作为输出量过于抽象，没有直接判定依据。但从蓄电池的工作原理以及失效衰退机制来看，预测蓄电池使用寿命可以等价于预测蓄电池的剩余容量。蓄电池剩余容量可以准确反映出蓄电池的真实工作状态，故输出量为剩余容量（q/Ah）。

明确输入量和输出量后，通过Matlab 神经网络工具箱，建立LS-SVM 系统，不同的核函数具有不同的特性，适合于不同的场景。在该蓄电池剩余容量预测模型中，核函数是由多项式核函数和RBF核函数组成的混合核函数。混合核函数能提高实验精度，是对单一核函数的优化改进。同时，在模型建立好后，根据预测值与实际值所计算的相对误差来判定模型的可行性指标。

3.4 系统测试

实验步骤如下：

1）求解权重系数及待优化变量a、b、c、d、g。给定被识别参数的初始值，即一个充分小的实向量并设定相对误差数值，通过求参数的当前运算值与上一次运算值的差值跟踪极值，求出参数相对变化量，把新获得的参数作为下一次递推的旧参数，不断地更新自身数值直到收敛情况满足要求，终止计算。各次参数的识别过程如图2所示。

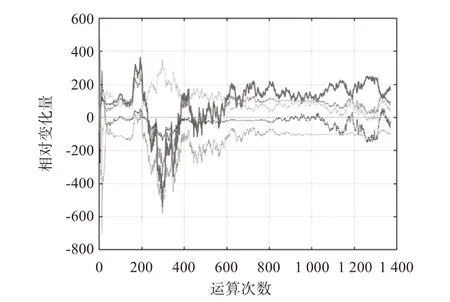
图2 递推最小二乘参数识别

2）在LS-SVM 模型中逐一带入求得的变量及各个参数，完善整个模型后输入测试样本的数据，通过模型运算预测出蓄电池的剩余容量。在实际测量中，用直流钳形表测量工作电流，用四位半数字万用表测量工作电压，另外需要计时器记录蓄电池充电时间，用温度计记录环境温度，并保持环境温度为25℃左右。在测量蓄电池容量时，调整直流供电系统中整流器的输出电压至过放保护电压，在蓄电池电压稳定后，打开整流器，对蓄电池进行均衡充电至蓄电池充满电，充电电流波动不得超过规定值的1%。蓄电池容量为充电电流与充电时间之积。使用该方法需考虑蓄电池与供电回路低压工作门限，这可能会影响其他设备，故不能作为日常检测方法。蓄电池的SOH计算公式为

式中，SOH为当前状态值；SOH0为起始状态值，SOH0=1；C为电池额定容量；η=充电电流 额定容量。

UPS 电源选取型号为SUA2200UXICH 的APC 在线式UPS 电源，内置蓄电池的标称电压为48 V，标称容量为100 Ah，单格标称电压为12 V，单格标称容量为100 Ah（共4 个单格）的卧龙灯塔蓄电池的型号为6-GFM-100。蓄电池在系统中作为备用电源，在系统正常运行时蓄电池处于浮充备用状态，在发生交流电失电或其他事故时蓄电池成为唯一供电设备。蓄电池样本实测数据如表1所示。

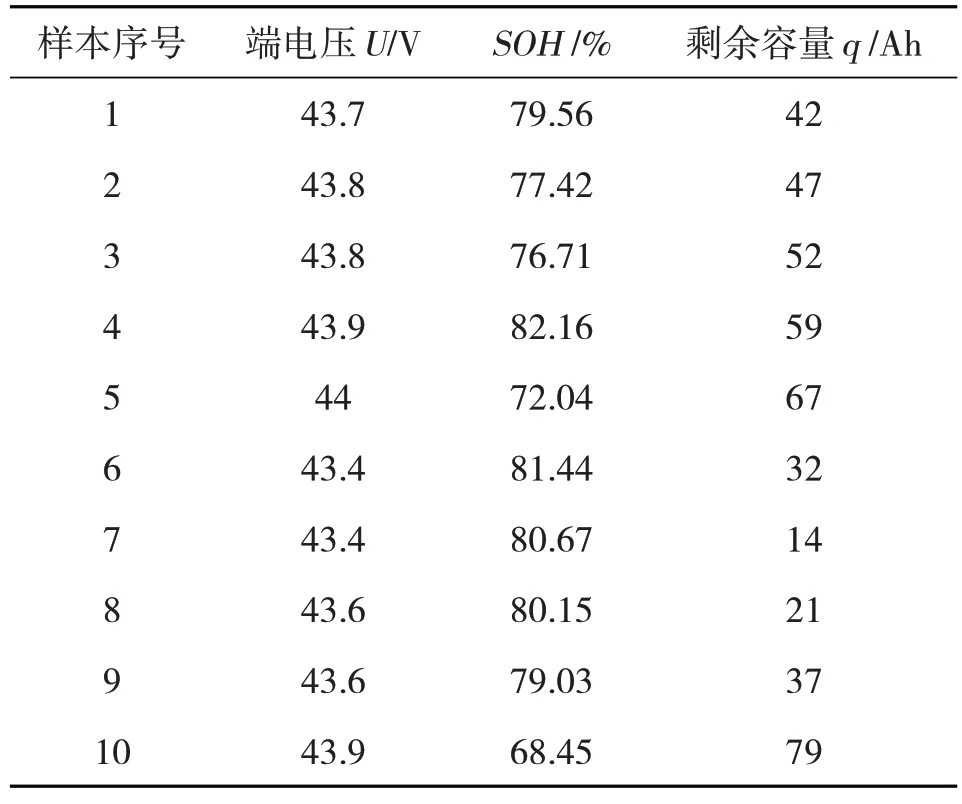
表1 样本实测数据

根据蓄电池模型建立等效方程式，搭建的蓄电池仿真模型可以有效仿真出蓄电池的极化反应及蓄电池动态性质。蓄电池仿真模型如图3所示。

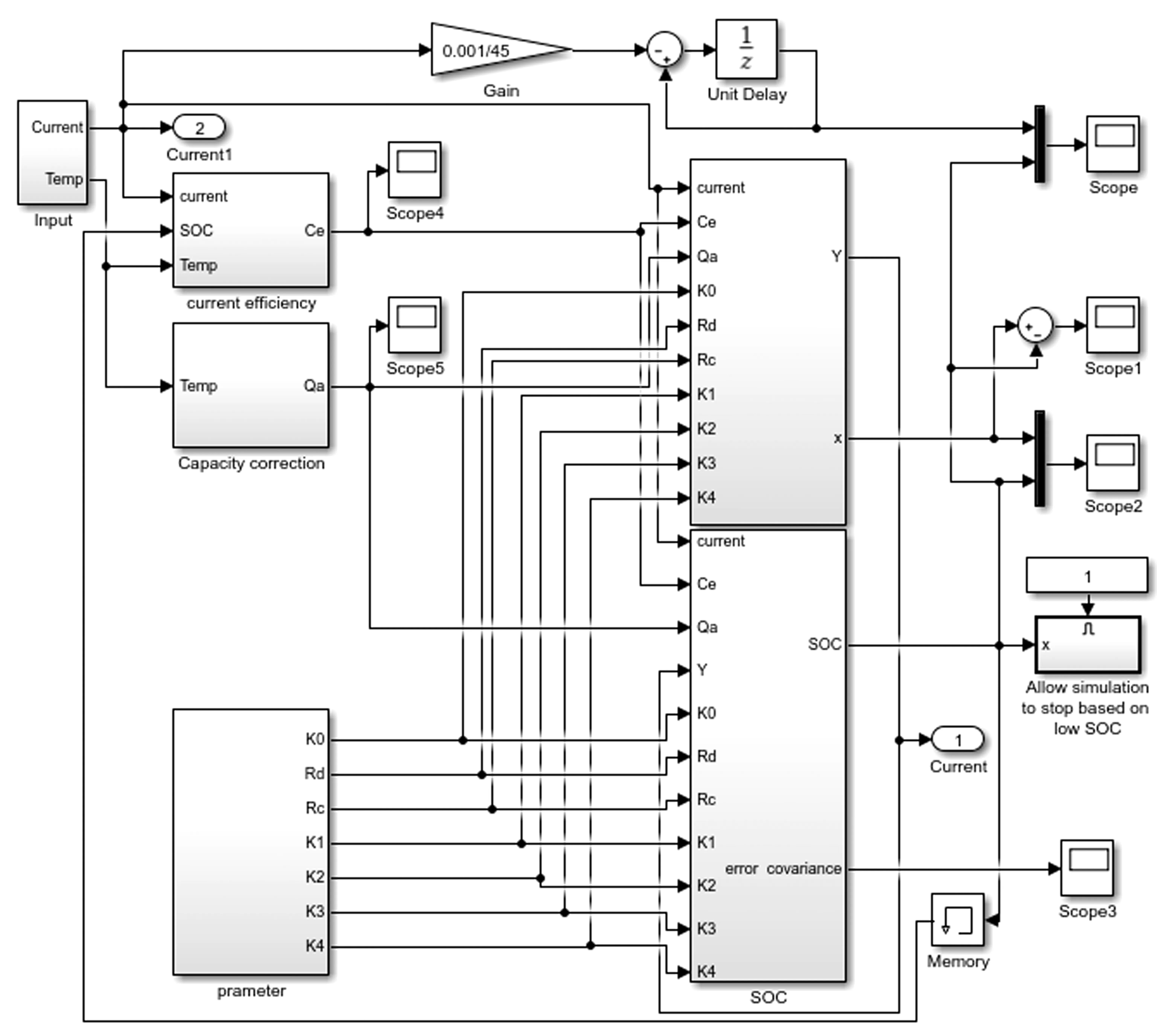
图3 蓄电池仿真模型

将实测数据中不同序号样本的端电压与SOH输入到LS-SVM 模型中，获得样本输出量，即各序号样本剩余容量预测值。将通过模型得到的预测值与实际值进行比较，并用图直观表达出来，如图4所示。

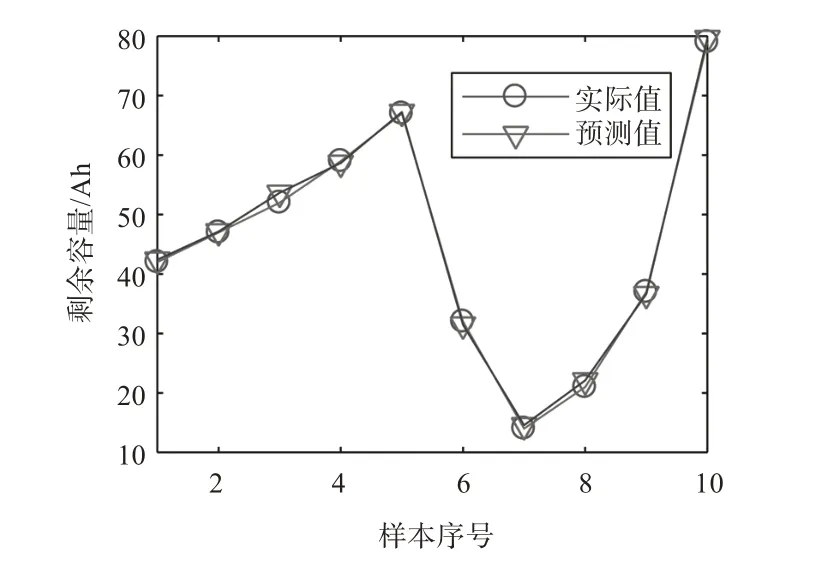
图4 预测值与实际值

3.5 实验分析

平均误差函数应当能够反映出不同参数下LS-SVM的泛化能力，也是判定模型可行性以及准确性的重要标准。通过式（10）计算基于该蓄电池寿命预测模型下的系统平均误差：

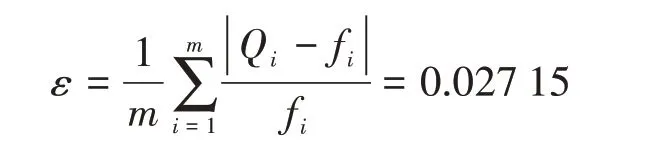
通过系统平均误差可以看出，由蓄电池寿命预测模型得出的预测值与实际值之间的平均误差为0.027 15。同时，规定电池寿命以剩余容量下降到标称容量的60%为终止点。根据实际值得到除序号5、序号10外，其余序号的蓄电池都需要更换，而根据预测值也得到了同样的结论，预测结果与实测结果一致。这表明了使用LS-SVM 模型预测蓄电池剩余电量的方法精度高，预测结果准确。

4 结语

系统介绍了影响蓄电池使用寿命的因素，并分析当今蓄电池在线监测现状。利用最小二乘支持向量机法，通过求解线性微分方程迭代出最优参数解，并对蓄电池剩余容量进行预测。通过分析实验结果可知，在蓄电池寿命预测问题上使用该方法能大大提高预测精确度，极大程度上减少了预测值与实际值之间的误差。