日光温室水幕的液膜强化换热特性研究

张皓男，王国峰，赵巧男，徐有宁，张文瀚，郭雨威

（沈阳工程学院a.能源与动力学院；b.工程技术研究院，辽宁 沈阳 110136）

近年来，强化换热作为传热学应用最为广泛的概念之一，因其对工业发展起到重要作用而受到研究者的广泛关注［1-2］。其中，液膜强化换热凭借流量小、传热系数大等优势，在众多研究者的共同努力下得到了良好发展［3-6］。

国内外学者从多方面入手，对液膜强化换热理论进行了深入研究［7-9］。其中，HOCD 等以数值模拟方式对水幕模型进行研究，提出了相应多相流水幕的数学理论公式［10］。邱庆刚等通过建立三维数学模型，研究了常温常压下液膜平板的流动，发现液膜的速度、温度及其分布是影响液膜强化传热的关键因素［11］。孙凤丹等发现液膜厚度会影响液层的传热能力，液膜厚度过大，会因热阻增大而不利于传热；液膜过薄，会造成液面波动［12］。目前，液膜强化换热理论大多应用于工业领域，而在农业方面应用较少，将这种理论运用到日光水幕温室的水幕强化换热相关研究中，会增强水幕单位面积的换热能力，进而增大水幕总体的换热量［13-14］。AL‐BERT C等利用N-S方程研究了温室内部的温度变化与水幕入口水温、温室外气温的关系，发现水幕作为换热介质存储热量是一种较为常见的蓄热方式，水幕利用水的流动性与传热系数大的优势进行强化换热［15］。综上所述，本文将温室水幕概念与液膜强化换热理论相结合，在一定程度上可以显著提升单位时间的换热量，以达到增加总换热量的目的。

1 气水域流体换热数学模型

气水域流体换热模型是全水域流体换热模型的一种改进模型，不但考虑水层流动作用，还考虑到水层与空气层的对流作用，可以更加准确地还原水幕模型。气水域模型中的气水两相流为多相流模型中的一种，如图1 所示。与全水域强化换热模型相比，这种模型多了空气相，流体之间、流体和壁面之间的对流换热情况较复杂，不能直接简化成平板换热模型，难以用理论推导的方式进行分析，但可以用全水域的数值解法来分析。

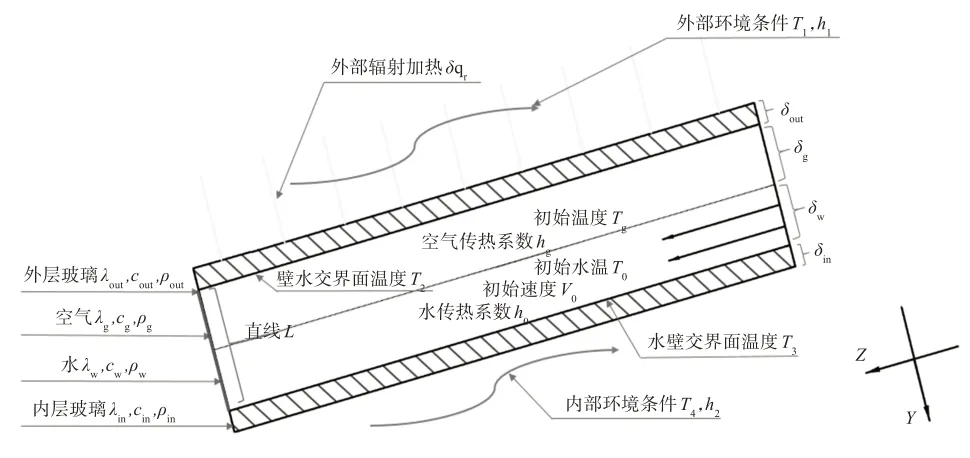
图1 气水域流体换热模型

为了分析气水域的性质，以多相流的N-S方程来计算气水域强化换热模型。气水域模型既需要计算玻璃层与水层的热传导，又需要研究水层、玻璃层以及空气层间的对流作用对解的影响：

1.1 模型建立

气水域水幕物理模型是从全水域水幕模型改进而来，所以只需在全水域水幕模型中加入空气层，如图2所示。

图2 气水域水幕物理模型

计算域长L为1 000 mm，宽D为400 mm，初始空气层厚度δg为5 mm，初始水层厚度为5 mm，计算域与水平面的夹角α为25°。

1.2 网格划分

结构化网格的特点为节点连接方式稳定不变，生成速度快，质量较好，数据结构简单，很容易实现边界拟合。对气水域模型的网格划分选用六面体结构化网格，虽然在建模过程中以slice 命令分成两部分，但上下两部分完全一致，所以划分网格时可以同时进行。使用Edge Sizing 与Face Sizing 相结合的方式，最终确定网格数量为425 320，对模型的各边及各顶点进行网格加密处理，网格质量较高，如图3所示。

图3 气水域水幕模型网格

1.3 参数设置

将水幕换热模型的网格导入Fluent软件，选择三维模型计算方法，计算精度为双精度，使用Vol‐ume of Fluid 模型、Standard k-e 模型、Radiation 模型与Energy模型，并利用瞬态求解器求解。

1.4 模拟结果分析

1.4.1 水的体积分数及温度关系

图4 为V0=0.3 m/s、V0=0.6 m/s、V0=0.9 m/s时，直线L上水的体积分数、温度与位置关系。

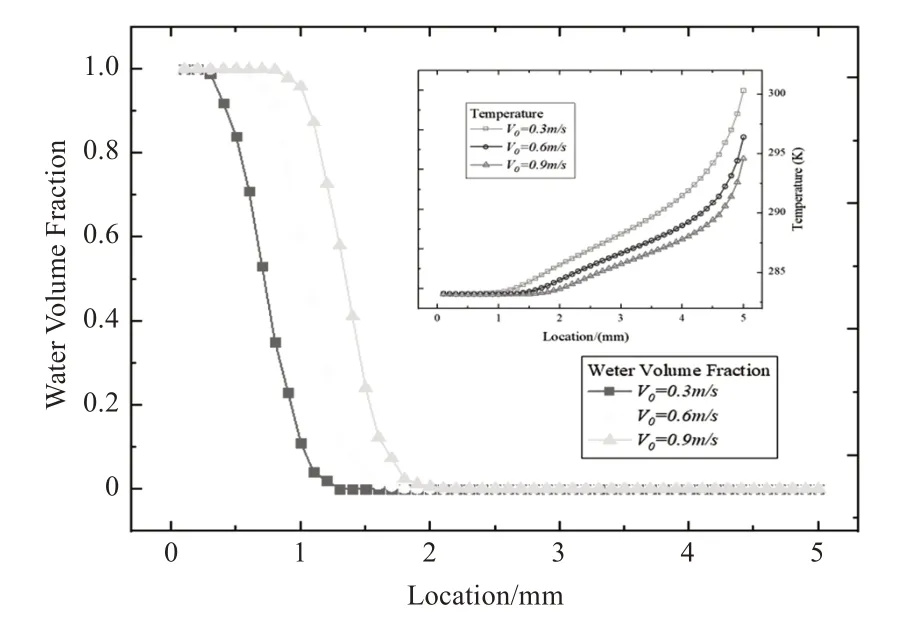
图4 直线L上水的体积分数及温度分布

3 条实心点线表示水的体积分数与位置的关系。水的体积分数为1 时，该点处全部充满水；水的体积分数为0 时，该点处充满空气；当水的体积分数为0～1 时，为水和空气的混合物。水层越薄，曲线从1 降到0 的速度越快；水层越厚，曲线从1 降到0 的速度越慢。由图4 可知，当V0=0.3 m/s 时，曲线下降速度最快。水层最薄；当V0=0.9 m/s 时，水层最厚。因此，水层厚度随初始速度增大而增大，速度越大，水层厚度越接近于液膜的初始厚度。

3 条空心点线表示温度与位置的关系。当V0=0.3 m/s 时，温度上升最快且温升幅值最大；当V0=0.6 m/s 时，升温速度稳定，但与V0=0.3 m/s 时相比较慢；当V0=0.9 m/s 时，温度升高速度最慢且温升幅值最小，即流体层温度随初始速度增大而减小。这种现象是由于水幕的初速度越小，水在模型中加热的时间就越长，收到太阳辐射的换热量越多，所以温度越高。

1.4.2 热流量与初始速度的关系

图5 为该模型在不同时间点，通过模型的热流量与初速度关系的折线图。横坐标为初速度，纵坐标为热流量。若各时间点上热流量数值相近，说明保持该初速度不变时，水幕换热稳定；若各时间点上的热流量数值相差较大，说明在该初速度下的换热不稳定。

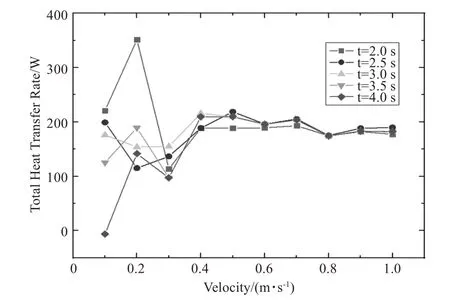
图5 热流量与初始速度、时间关系

当V0≤0.3 m/s 时，各时间段热流量相差较大，由于初速度过小，水层无法覆盖整个水幕的情况，使得热交换不稳定；当V0＞0.3 m/s 时，各时间点上的热流量值波动较小。由图4 可知，当V0＞0.4 m/s时，水幕铺满模型底部，液面较为稳定，换热较为均匀，总体换热量为170 W～220 W。当V0=0.8 m/s时，热流量值较为稳定，但数值较小；当V0=0.5 m/s 时，热流量值相对较大，且0.2 s 之后较为稳定。所以，继续分析V0=0.5 m/s附近的初速度。

综上所述，在气水域流体换热模型中，初速度越小，水层厚度越小，温升越快且数值越大，但热流量越不稳定；初速度越大，水层厚度越大，温升越慢且数值越小，但热流量趋于稳定状态。在分析气水域换热时，应选择热流量稳定且温升较大的初速度作为基础数据，以此分析得到的热流量和温度等数据作为基于液膜理论强化换热模型的研究基础。

2 基于液膜作用的气水域流体强化换热模型

为进一步增强水幕换热能力，引入液膜理论，建立考虑液膜作用的气水域流体强化换热模型。液膜理论基于流体的粘性作用，粘性导致液体在流动过程中产生剪切力，可延长液体向下流动的时间。当液体流动速度较小时，液体吸收板层热量，减少板层散热量，可达到增强换热量的目的。利用数值解法对基于液膜作用的气水域模型进行求解，并与不考虑液膜作用的气水域模型进行对比，分析在液膜作用下不同的初速度对出口温度、液膜厚度、壁面热流量以及壁面对流传热系数的影响。

2.1 控制方程与边界条件

液膜作用适用于低流速流体换热，将这种作用运用到气水域强化换热的相关研究中，能够增强水幕单位面积的换热能力，进而增大水幕换热量。该模型考虑液膜作用对流动的影响，得出液膜关于液膜厚度的N-S 方程如下，并代入公式（1）～（3）的源项中：

式中，H表示液膜厚度表示液滴的速度向量；∇s表示表面梯度算子表示液滴撞击到壁面的源项；Ts表示水和空气交界面温度；Tf表示液膜的平均温度；T3表示下层玻璃板表面温度。

2.2 模拟结果分析

由式（4）～（6）可知，速度决定液膜厚度，液膜厚度影响换热能力。针对水幕气水域液膜换热进行数值模拟，可得到液膜作用对温度的影响，并分析在不同初速度下液膜厚度、壁面热流量和壁面对流换热系数的变化情况。

2.2.1 液膜作用对温度的影响

图6 是液膜作用与速度对水层温度的影响示意图。横坐标为入口初速度，左侧纵坐标为出口水温，右侧纵坐标为基于液膜作用的气水域水幕出口水温与不考虑液膜作用的气水域水幕出口水温之差。

图6 液膜作用与速度对水层温度的影响

Film Temperature 是基于液膜作用的气水域水幕出口水温；Water Temperature 是不考虑液膜作用的气水域水幕出口水温；曲线是考虑液膜作用出口水温度升高值。对于考虑液膜作用的气水域模型和不考虑液膜作用的气水域模型，水的温度均随入口速度增大而降低。当入口初速度较低时，随着初速度增大，基于液膜理论的水幕温升数值下降快；当入口初速度较高时，上下曲线近乎平行，温升数值下降速率近乎相同。通过比较考虑液膜作用的出口水温与不考虑液膜作用的出口水温之差发现：当V0=0.3 m/s 时，温差最大，为0.083 K；当V0=0.4 m/s 时，温差降低较多，为0.062 K；当V0≥0.5 m/s 时，温差保持在0.051 K 左右，波动很小，总体数值趋势呈指数下降。由于低流速范围内水层的液膜作用，水层与玻璃板间产生粘性剪切力，减小水层向下的速度。因此，当入口初速度较大时，温差趋于平稳。

综上所述，水幕的换热量与吸收阳光辐射的时间有关，当入口初速度一定时，加速度越小，单位时间内速度越小，水流过壁面所需的时间越长，吸收阳光辐射的时间就越长，换热量就越大。但当V0=0.3 m/s 时，水层未能覆盖整个水幕，换热不稳定。所以，V0=0.4 m/s为更适合的初速度。

2.2.2 壁面热流量、壁面对流换热系数与初速度的关系

图7 为壁面热流量与X 轴方向上的位置关系。横坐标为X 轴方向上的位置，纵坐标为壁面热流量，7 条曲线分别为不同初速度下沿水流方向的壁面热流量。

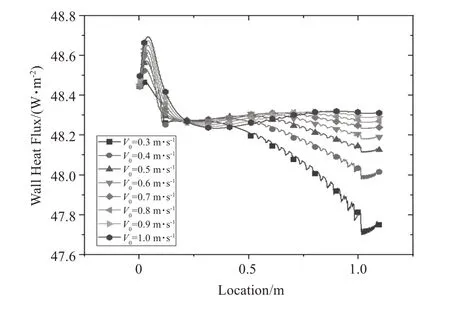
图7 壁面热流量与位置关系

如图7所示，总体趋势为随着水流方向，热流量递减。在Location为0.5 m附近时，初速度较高的水流热流量趋于平稳，初速度较低的水流热流量仍有很大的递减趋势。通过比较同一位置处不同初速度的壁面热流量可知，初速度越大，壁面热流量越大。壁面热流量在0.5 m～1.0 m范围内呈减小趋势，已知总热量保持不变，壁面热流量减小，则水的热流量就增大，即热量进入水层增多。在同一位置处初速度越大，壁面热流量越大；反之，壁面热流量越小。

图8 为壁面对流换热系数与X 轴方向上的位置关系。横坐标为X轴方向位置，纵坐标为壁面对流换热系数，7 条曲线分别为不同初速度下沿水流方向的壁面对流换热系数。

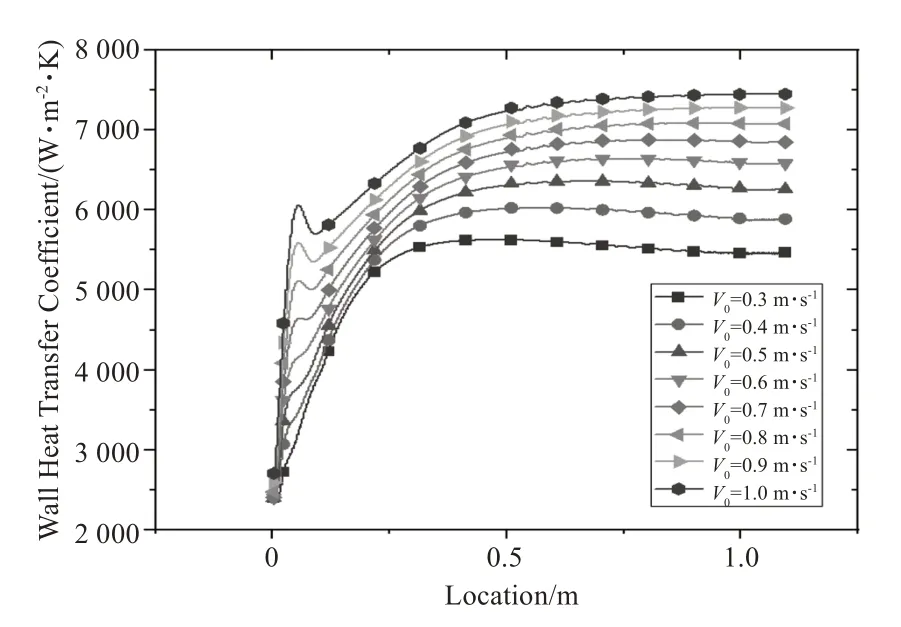
图8 壁面对流换热系数与位置关系

如图8 所示，在同一位置，从V0=1.0 m/s 到V0=0.3m/s，壁面对流换热系数依次减小，相邻曲线间壁面对流换热系数差值不断增大。这是由于初速度越小，液膜作用越明显，壁面对流传热占比越小。

综上所述，在基于液膜作用的气水域模型研究中，当水流在同一位置且已知总辐射量时，初速度越小，液膜作用越明显，下层玻璃板的壁面热流量与壁面对流换热系数越小，水层的热流量与对流换热系数越大。因此，在保证液面能够覆盖下层玻璃的情况下，选取的初速度越小越好。通过数值仿真结果可知：V0=0.4 m/s为最合适的初速度。

3 结论

本文以全水域强化换热研究为基础，应用数值模拟分析的方法，探究了应用于温室水幕的液膜强化换热理论，建立了基于液膜作用的气水域模型，列出了相应的控制方程，并比较考虑液膜作用的气水域水幕换热量与不考虑液膜作用的气水域水幕换热量，以此验证了液膜作用对强化换热的影响。最后，分析了基于液膜作用的强化换热模型在不同出口温度、液膜厚度、壁面热流量以及壁面对流传热系数影响下的强化换热效果，所得结论如下：

1）在气水域流体模型中，初速度越小，水层厚度越小，温升越快且数值越大，但热流量越不稳定；初速度越大，水层厚度越大，温升越慢且数值越小，但热流量趋于稳定状态。当V0=0.5 m/s 时，热流量值相对较大且较为稳定，可以继续分析0.4 m/s ≤V0≤0.6 m/s的情况。

2）在基于液膜理论的气水域水幕换热模型中，初速度越小，液膜作用效果越明显，由液膜作用产生的温度升高值越大，壁面热流量以及壁面对流传热系数均越小；但当初速度过小时，水层不能覆盖整个水幕，造成热量损失。所以，在分析基于液膜理论的气水域水幕换热时，V0=0.4 m/s 为最合适的初速度。