基于PSO-BP 神经网络的增量式拉线位移传感器误差补偿方法*

徐 峰，姚恩涛，冯嘉瑞，曹智超

(南京航空航天大学自动化学院，江苏 南京211100)

拉线位移传感器具有成本低、动态特性好、安装简便等特点。 拉线变形产生的误差、增量式旋转编码器的装调误差、制造误差和细分误差均会对拉线位移传感器的精度造成影响。 为获得高可靠性、高精度的位移信息，需要对拉线位移传感器的误差进行补偿。 文献[1]提出一种动态测量误差补偿方法，建立拉线加速度与受力关系、变形量与受力关系的数据库，再通过计算得到实际位移量，实现了动态补偿。 文献[2]发明了一种修正工具，采用了一种工具与软件结合修正分辨率的方式来修正误差。 文献[3]指出拉线位移传感器精度的提高，可通过提高其核心部件即内部编码器的精度来实现，通过增加编码器码道数目来提高精度，减小测量误差。 上述文献未对拉线与编码器的误差情况进行重点分析，虽然在一定程度上补偿了误差，提高了精度，但需要额外的设备或建立庞大的数据库体系来协助补偿。 本文基于拉线位移传感器的测距原理，对拉线位移传感器误差来源进行了研究，并提出一种基于PSO-BP 神经网络模型的误差补偿方法对拉线位移传感器的误差进行补偿。

1 误差来源

1.1 拉线误差

拉线处于水平或倾斜位置时，受重力和拉线盒内部弹簧拉力的作用，将下垂弯曲，且当测量位移发生变化时，其挠度也在非线性变化。 由于拉线位移传感器测量的是拉线长度，并非两点间直线距离，产生了测量误差，由于重力方向确定，该误差方向也确定，即测量值相比于真实值偏大。

做出如下假定:假定拉线是一根处处铰接的柔软链条，那么拉线仅受到轴向张力和重力，不承受弯曲力矩。 拉线受到的重力垂直向下，并沿拉线长度均匀分布[4]。

在测量某一直线距离时，将拉线一端固定，另一端拉至测量位置，为了确认此时拉线的实际长度，将拉线近似等效为以下模型，如图1 所示。

图1 拉线模型

其中，B点固定，为拉线位移传感器出线口位置，A点为测量点，设该点受拉力F，方向为拉线在A点的切线方向。 设直线AB为待测距离，长度为L，AB与水平线夹角为β。 由于拉线受自重影响，会产生下垂弯曲，即弧线AB，设其长度为S，即拉线位移传感器测量值，此时弧线在A点处的切线与水平线夹角为α。

根据悬链线长度公式:

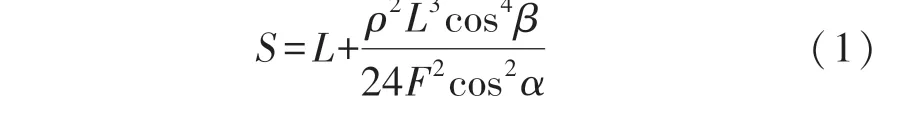
式中:ρ是拉线单位长度质量(kg/m)。

拉力F的大小与拉线长度有如下关系:

k为弹簧劲度系数，Δx为弹簧伸长量。

当位移为水平方向时，即β＝0，悬链线长度公式如下:

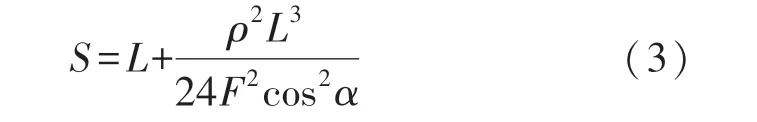
α与F的关系如下:

分析式(1)～式(4)可得出由拉线形变引起的测量误差el，与拉线拉出长度S、拉线单位长度质量ρ和轮毂弹簧劲度系数有关，即:

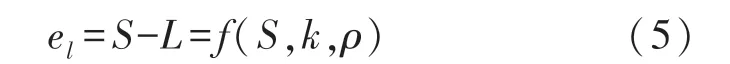
且拉线弯曲引起的误差和拉线拉出的长度及拉线单位长度质量呈正相关，与编码器轮毂弹簧劲度系数呈负相关。

1.2 编码器误差

拉线位移传感器的测距原理是将直线位移转化为编码器轴的旋转运动，其核心部件是增量式旋转光电编码器。 故光电编码器引起的误差将导致拉线位移传感器的总误差增大。 光电编码器的精度取决于机械因素，主要体现在编码器制造、装配、元器件的选型等方面，误差可分为码盘的偏心误差、制造误差和细分误差等[5]。

偏心误差产生的原因是码盘的中心位置和转动中心不重合，如图2 所示。

图2 安装偏心示意图

设码盘的中心为O，旋转中心为O′，两点距离为f，刻线的长度为l，光栅外径为r，则产生的偏移相移Δθ为:

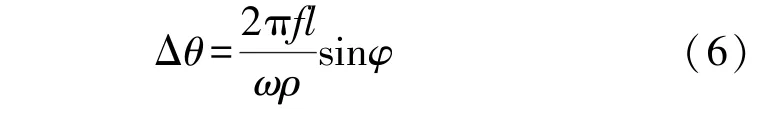
码盘的制造需要光刻设备进行刻线，受光刻设备自身误差影响，刻线的位置、方向与标准情况相比有一定偏差，将影响输出的莫尔条纹的质量。

莫尔条纹信号偏离理论波形较大，甚至产生严重失真，将会导致细分误差的增大。 莫尔条纹信号包含多种信号成分，表达式如下:

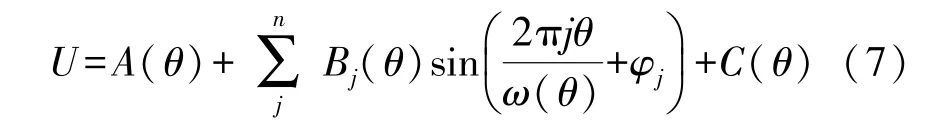
式中:A(θ)为直流分量，Bj(θ)为交流分量，ω(θ)为光栅角栅距，C(θ)为干扰噪声信号。 这些信号都不是恒定值，而是光栅角度位置θ随时间变化的函数。这些变化会影响莫尔条纹信号的质量，导致测量角位移时产生误差。

设两路细分信号分别为标准正弦信号，表达式如下:

式中:θ0为理论转角，表达式为:

实际信号的振幅并不是恒定值，而是受电源的稳定性、发光设备的发光强度以及环境温度等因素影响而变化，并且实际莫尔条纹信号与标准正弦信号相比有一定偏差[6]，设两路信号的表达式如下:

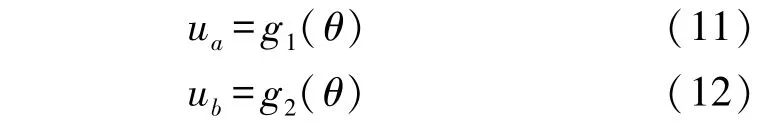
则实际细分相角表达式为:

细分误差为:

2 基于PSO-BP 神经网络的误差补偿模型

拉线位移传感器在实际测量位移的过程中，由于测量值会受到拉绳、编码器、安装位置及环境因素的影响，测量误差具有非线性和随机性[7-8]，而BP神经网络在非线性函数方面有较高的处理能力。

BP 神经网络的本质是梯度下降算法的多层迭代前馈网络[9]。 当网络正向传播时，通过提供大量输入实例至输入层，再传递至隐含层进行计算，最终由输出层输出计算结果，通过定义损失函数L(＾y(i)，y(i))和成本函数J(w，b)分别衡量网络在单个和全体训练样本上的表现[10]。 由于拉线式位移传感器的误差具有非线性，本文采用sigmod 函数[11]作为激活函数，采用交叉熵损失函数作为损失函数，其具有收敛速度快和更容易获得全局最优的优点，成本函数为所有样本损失函数之和的平均值:

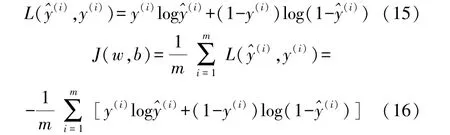
由成本函数得到累计误差，基于累计误差最小化的更新原则调整各神经元的权值和阈值。 如此反复迭代学习与调整参数，累计误差将减小到预定范围。 权值和阈值的调整公式如下:

BP 神经网络在训练时，与权值和阈值相关的成本函数通常未知，为保证收敛性，学习率相对较小，因此收敛速度较慢，迭代次数上升，效率极大下降。另外，梯度下降法本身存在弊端，训练时易陷入局部最小值，通常与网络的初始阈值和权值的选取有关，选取不当将无法得到最优解。

为解决上述问题，本文采用粒子群算法[12]对BP 神经网络进行优化。 粒子群算法具有较强的全局搜索能力[13]，能够提高BP 神经网络的训练速度，并且避免了权值和阈值的初值选取不当造成的易陷入局部最小值的问题。

PSO 算法对于指定的待优化问题，设定每个粒子定义为待搜索空间内存在的潜在解，粒子记忆其历史最优位置和全体粒子最优位置。 在每一次迭代过程中，粒子的信息被整合起来，调整每一维上的速度，进而更新粒子位置，通过多次迭代，各个粒子位置逐渐趋近最优解[14]。 算法公式如下:

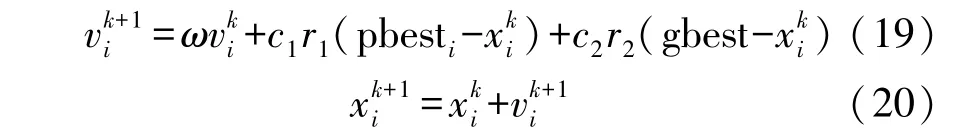
式中:ω为惯性权重，c1、c2为学习因子，r1、r2为介于(0，1)之间的 随机数，分别为第k、k+1 次迭代过程中粒子i的速度，分别为第k、k+1 次迭代过程中粒子i的位置，pbesti为个体最优位置，gbest 为群体最优位置。

本文采用的PSO 算法对BP 神经网络优化的策略是对初始权值和阈值进行优化，将全体样本的BP神经网络的输出和实际值的误差平方和的平均值作为适应值，通过不断迭代，搜寻全局最优解使适应度值逐步减小[15]。 适应度函数如下:

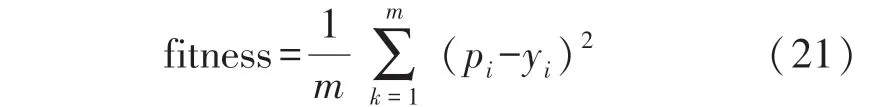
式中:fitness 为适应度值，m为样本个数，pi为样本输出，yi为实际值。

PSO 算法优化BP 神经网络的流程如图3 所示，流程如下:

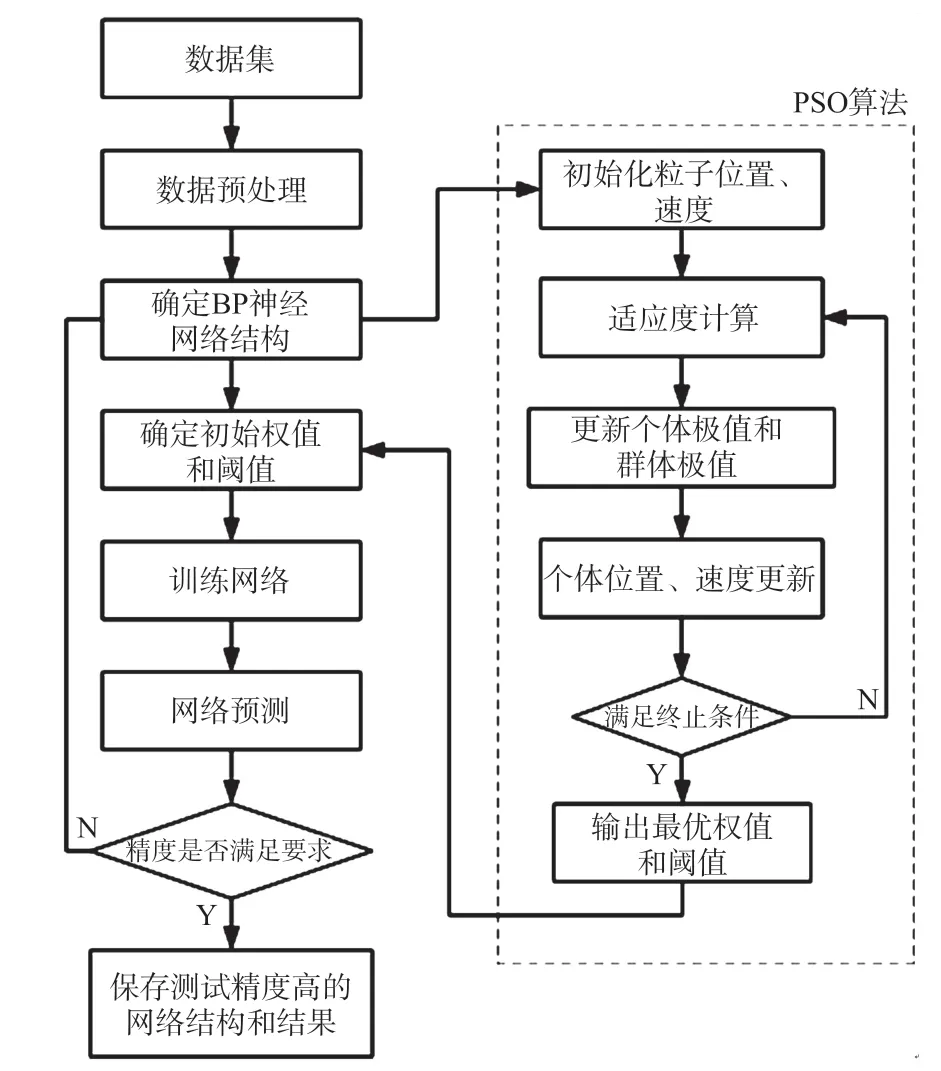
图3 PSO 算法优化BP 神经网络的流程图

①对样本数据预处理，并按9 ∶1 比例划分为训练集和测试集。

②初步确定BP 神经网络的结构，设定隐含层和输出层的激活函数与成本函数。

③设置PSO 算法的种群粒子数和迭代终止条件，优化初始权值和阈值。

④将优化过的权值和阈值作为BP 神经网络的初始权值和阈值，使用训练集进行网络训练，将训练后的网络相关参数保存。

⑤使用测试集对BP 神经网络进行测试，若测试精度在可接受范围内，则保存结果。 否则，更改神经网络结构，返回步骤③。

3 实验及数据处理

3.1 实验装置

本文被检测的拉线位移传感器为KS120 系列拉线位移传感器。 在实验中采用LT-P2250 型高精度激光位移传感器进行标定，其分辨率为1 nm，重复精度为250 μm，线性度为0.03% FS，该传感器可进行高精度的非接触测量，且具有高速、高灵敏度的测量性能，故将其测量值作为约定真值。 实验装置原理框图如图4 所示。

图4 实验装置原理框图

传感器检测装置由被检测拉线位移传感器、计算机、MCU、激光测距仪、电机和滑块、导轨等组成。上位机计算机与MCU 通过232 总线通信，可设定传感器的检测次数及测量位移等。 MCU 接收上位机的采集指令，控制电机带动滑块在导轨上运动并在测量点处停止，通过采集拉线位移传感器的脉冲信号获取测量位移，与激光测距仪通过485 总线进行通信，获取位移真值，最后将测量值和真值上传至上位机计算机储存，用于研究传感器的误差补偿。

3.2 误差表示

传感器误差可由绝对误差e、平均绝对值误差MAE(Mean Absolute Error)[16]和 标 准 偏 差σ来表示。

绝对误差e反应测量值偏离真实值的大小和方向，表达式如下:

式中:x为待测物理量的测量值，a为其真值。

平均绝对值误差MAE 表示在一组n次测量中，各次测量的绝对误差的绝对值的平均值，表达式如下:

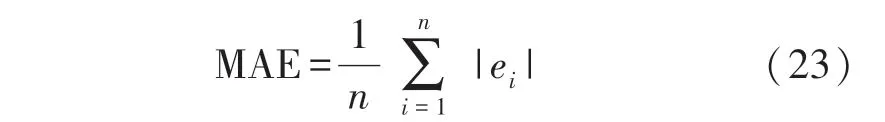
式中:n为测量次数，ei为第i次测量时的绝对误差。

标准偏差σ描述一组n次测量中，各绝对误差偏离平均绝对值误差的平均数，能够反应一个数据集的离散程度。 其表达式如下:

3.3 重复性测试实验

在拉线位移传感器量程范围内设置多个测量点，对每个测量点进行多组实验测量。 各个测量点的标准偏差和平均绝对误差如表1 所示，各测量点标准偏差和平均绝对值误差分别如图5、图6 所示。

图5 各测量点标准偏差

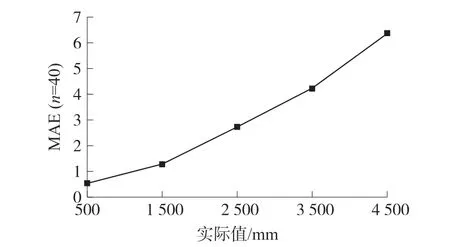
图6 各测量点平均绝对值误差

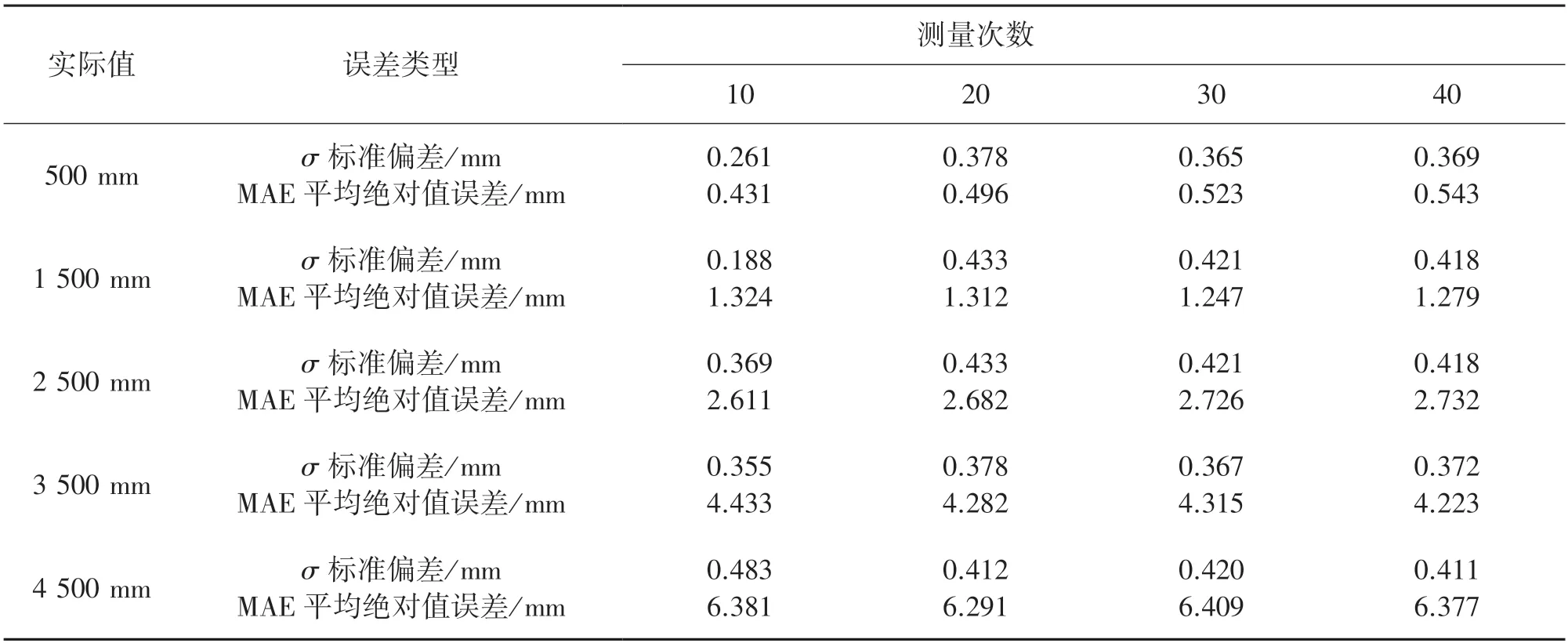
表1 各测量点标准偏差与平均测量误差

从实验数据和误差曲线图可看出，在量程范围内对某点多次测量，测量值的标准偏差趋于稳定，表明拉线位移传感器具有良好的测量重复性；其次，随着位移值的增大，平均绝对值误差也在增大，且具有一定的非线性特点。

3.4 误差补偿实验

为了尽可能多地获取全范围内的实验样本用于神经网络的训练，在拉线位移传感器量程范围内随机测量位移，并记录测量值和测量误差，共计400 组数据。 测量误差值如图7 所示，横坐标是测量位移，纵坐标是绝对误差。

图7 显示出在全量程范围内拉线位移传感器的误差在一定范围内波动，且测量位移越大，绝对误差越大，在一些要求高精度的场合使用时必须对其进行误差补偿[17]。

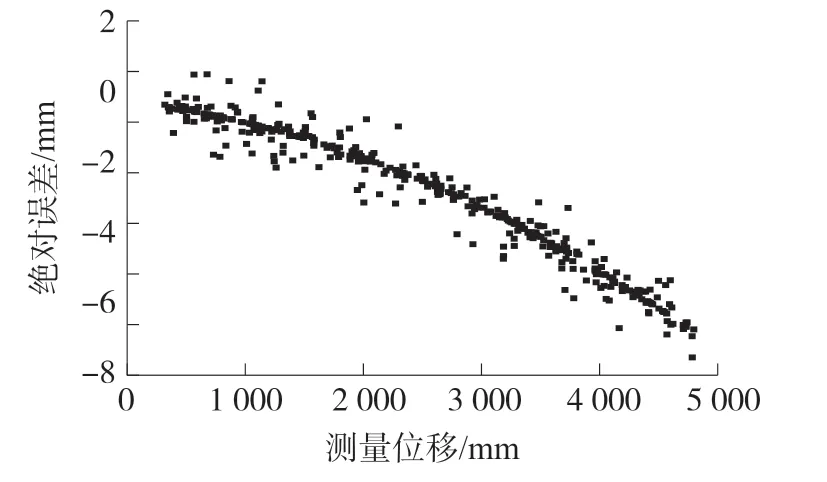
图7 拉线位移传感器全量程绝对误差情况

取其中360 组数据作为训练集输入到PSO-BP神经网络补偿模型中进行学习。 在PSO 算法中，设定种群规模为100，迭代终止条件为迭代100 次，惯性权重ω为0.6，学习因子c1＝c2＝2，初始化粒子的每一维位置和速度均为(-1，1)范围内随机数，将训练得到的群体最优位置作为BP 神经网络的初始权值和阈值进行训练，最终确定神经网络的隐含层节点为[10，15，5]，学习率α＝0.002。 再将40 组测试集输入到经过训练后的神经网络进行误差的预测，将其与未补偿的误差做比较并进行误差补偿。 基于PSO 的BP 神经网络预测能力和补偿前后的拉线位移传感器误差对比如表2 及图8 所示。

表2 PSO-BP 神经网络模型补偿前后误差对比

图8 和表2 显示出PSO-BP 神经网络补偿模型能够有效补偿拉线位移传感器测量误差，尤其针对较大偏差的补偿更加明显，平均绝对值误差和标准偏差显著降低。

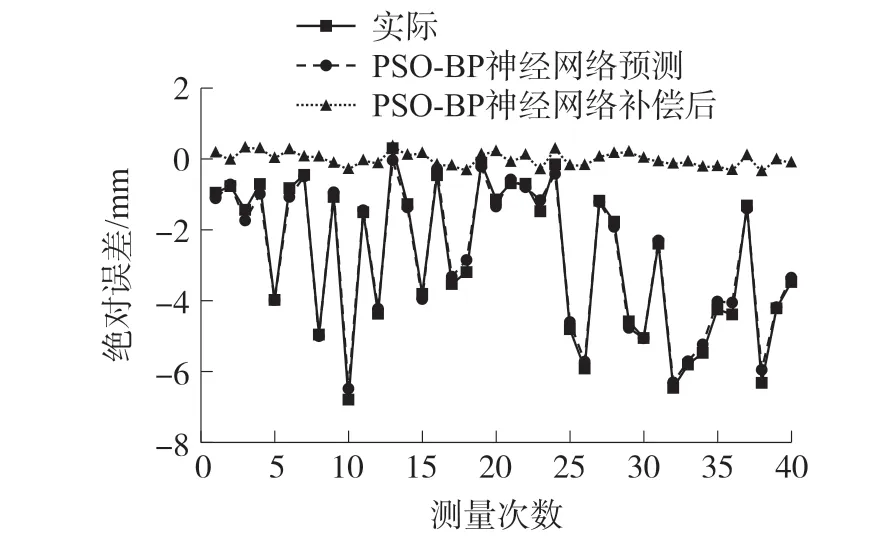
图8 PSO-BP 神经网络误差预测及补偿情况

3.5 补偿模型结果数据对比

将传统的多项式拟合模型和传统BP 神经网络模型应用于拉线位移传感器误差补偿，补偿结果如图9、图10 所示，并与本文PSO-BP 神经网络补偿模型进行结果对比，如表3 所示。

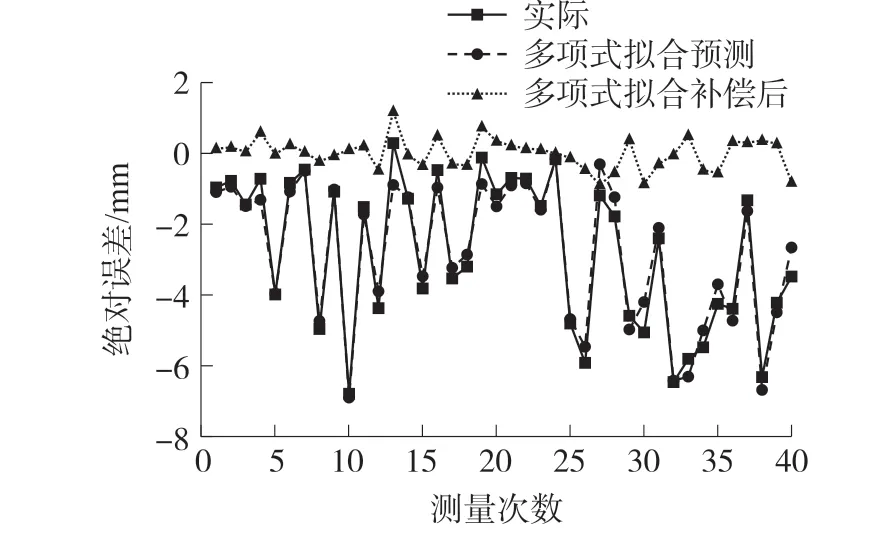
图9 多项式拟合模型误差预测及补偿情况

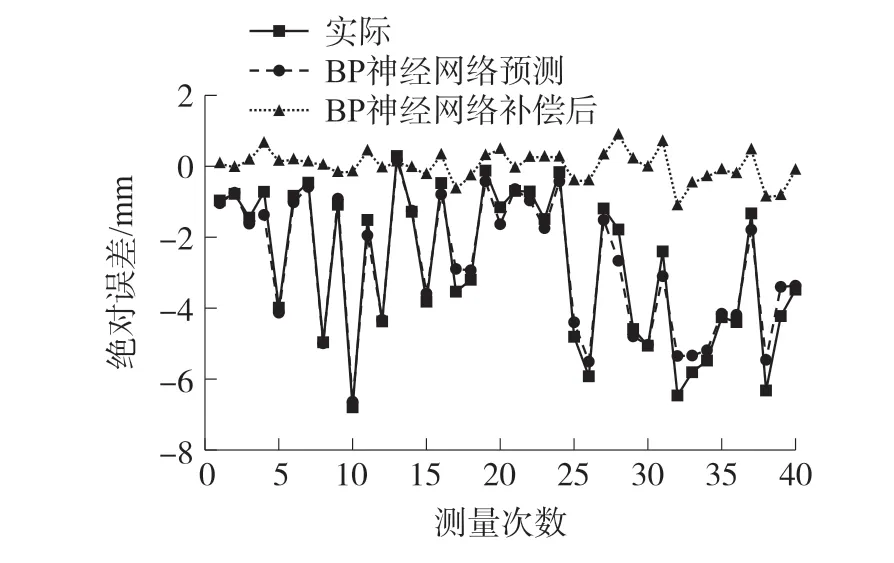
图10 BP 神经网络模型误差预测及补偿情况

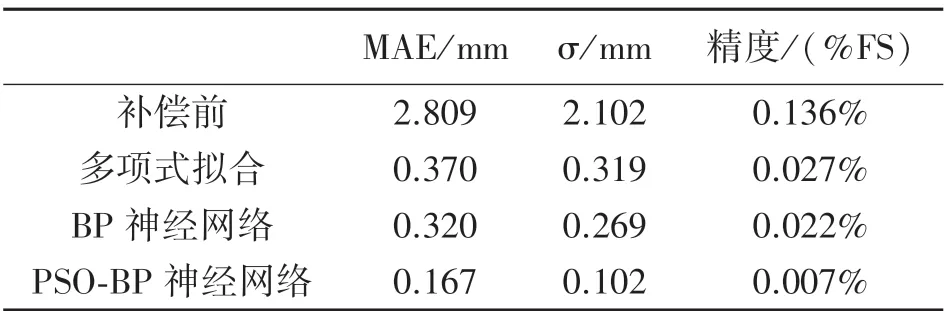
表3 各补偿系统误差补偿效果对比

从实验数据看出，经过PSO-BP 神经网络补偿模型的误差补偿后，测量误差显著降低，同未补偿时相比，平均误差降低到0.167 mm，标准偏差降低到0.102 mm，拉线位移传感器的精度由0.136% FS 提高到0.007% FS。 且相比于另外两种模型，具有更好的补偿效果。 多项式拟合的方法多适用于线性误差的补偿，拉线位移传感器的误差具有非线性，该模型修正效果较低。 传统的BP 神经网络由于初始权值和阈值的范围难以确定，多设定为随机值，在求解时容易陷入局部最小值，对于部分数据拟合情况不理想，造成个别样本偏差较大。 PSO-BP 神经网络补偿模型则解决了上述问题，由于PSO 算法优化了初始权值和阈值，在后续训练网络时学习效率有显著提升。

4 结语

本文分析了拉线位移传感器的误差来源，并设计了基于用PSO 算法优化初始阈值和权值的BP 神经网络误差补偿模型进行误差补偿。 将实验结果统计并建立数据集，对PSO-BP 神经网络进行训练，通过测试集对补偿模型进行测试。 将补偿前后的误差情况对比，平均绝对值误差由2.809 mm 降低到0.167 mm，标准偏差由2.102 mm 降低到0.102 mm，精度由0.136% FS 提高到0.007% FS，补偿效果显著，结果在可接受范围内。