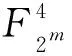基于密码结构完全置换多项式的构造

刘静琰，肖同飞，聂 顺，雷 卓，彭 昶，胡道欢，谢小雨，曹晓玉，许小芳*

(1.湖北理工学院 数理学院，湖北 黄石 435003；2.黄石市第十六中学，湖北 黄石 435000)

0 引言

完全置换多项式是一类特殊的置换多项式, 具有完全平衡性、雪崩特性等良好的密码学性质。因此，人们积极尝试将完全置换多项式应用于密码、编码及其组合设计等领域，如基于完全置换多项式的Lay-Massey密码结构[1]、流密码Loiss[2]、分组密码算法SM4[3]、秘钥扩展算法[4]等。我国基于完全置换多项式研发的SM4分组密码算法在2021年6月25日正式成为了ISO/IEC国际标准[3]。因此，研究完全置换多项式的构造具有重要的理论以及实际意义。

1942年Mann提出了完全置换多项式的定义，主要用于构造正交拉丁方[5]。1957年，Hall和Paige研究了有限群上的完全置换[6]。1982年，Niederreiter和Robinson首次详细地讨论了有限域上的完全置换多项式[7]。随着完全置换多项式的应用领域越来越广泛，其研究成果越来越多，主要集中在完全置换多项式的构造方面。比较有代表性的是：含有较少项数的稀疏型完全置换多项式[8-10]、形如(xpm-x+δ)s+L(x)的基于线性化多项式的完全置换多项式[11]以及完全置换多项式的递归构造。有关完全置换多项式的其他研究成果可参考文献[12]。

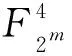
1 基础知识

符号F2m表示元素个数为2m的有限域，其中m是正整数。

定义1[3]如果有限域F2m上的多项式f(x)诱导的从F2m到其自身的映射f:c→f(c)是有限域F2m上的双射，则称f(x)为有限域F2m上的置换多项式。若f(x)和f(x)+x都是F2m上的置换多项式,则称f(x)为F2m上的完全置换多项式。

下面给出本文证明给定多项式为置换多项式所使用的准则。

引理1[3]有限域F2m上的多项式f(x)是F2m上的置换多项式，当且仅当下列条件之一成立:

1)对任意的y∈F2m,方程f(x)=y在F2m中恰有1个解。

2)对任意的y∈F2m,方程f(x)=y在F2m中至少有1个解。

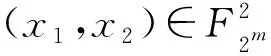
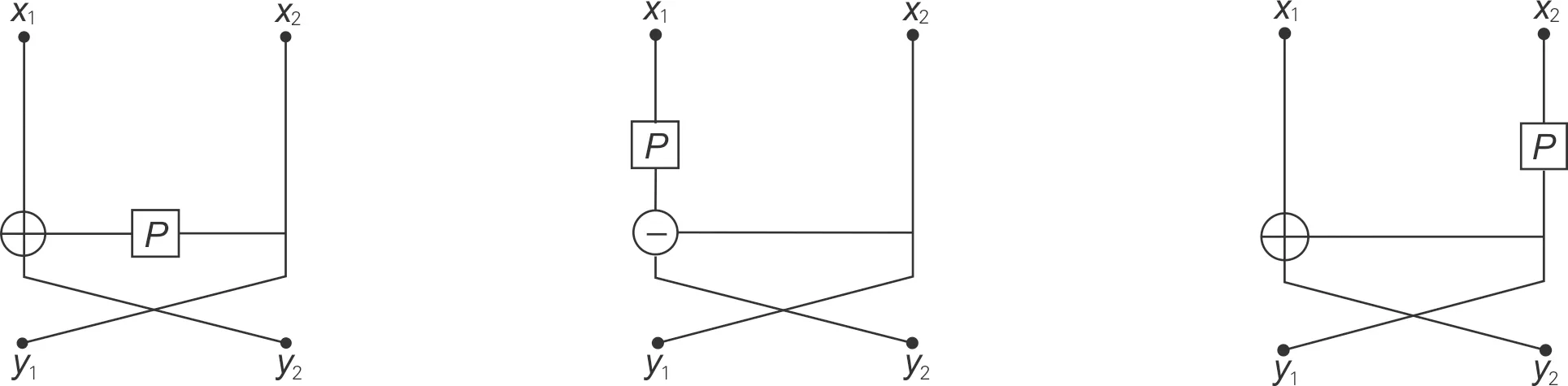
图1 1轮Feistel结构 图2 1轮L-MISTY结构 图3 1轮R-MISTY结构

2 基于4路两重Feistel结构和MISTY结构完全置换多项式的构造

在Feistel 结构、L-MISTY以及R-MISTY结构的基础上采用4路两重Feistel和MISTY结构来构造完全置换多项式。

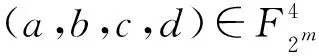
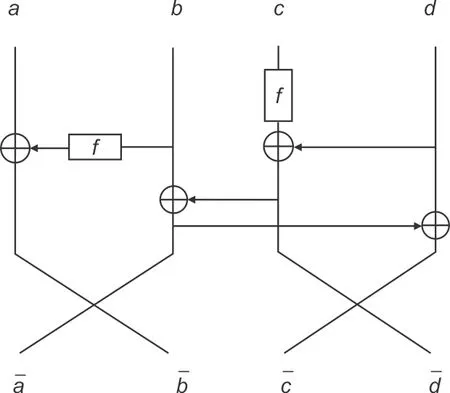
图4 省略轮秘钥的一类4路两重Feistel和L-MISTY结构

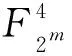
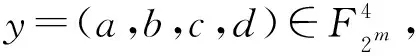
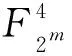
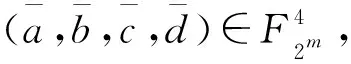
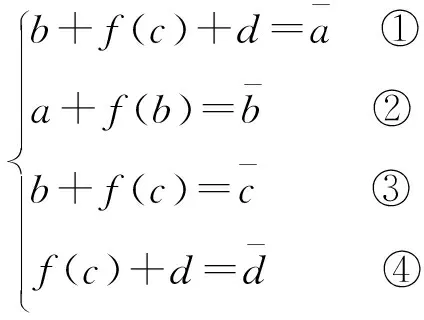
(1)

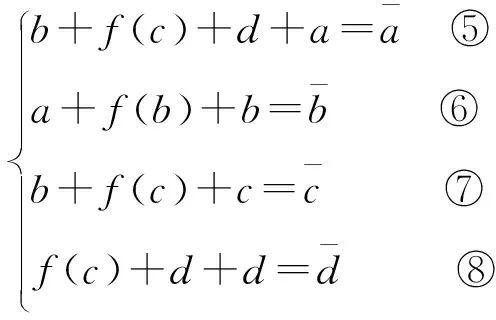
(2)

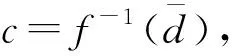
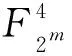
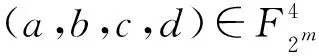
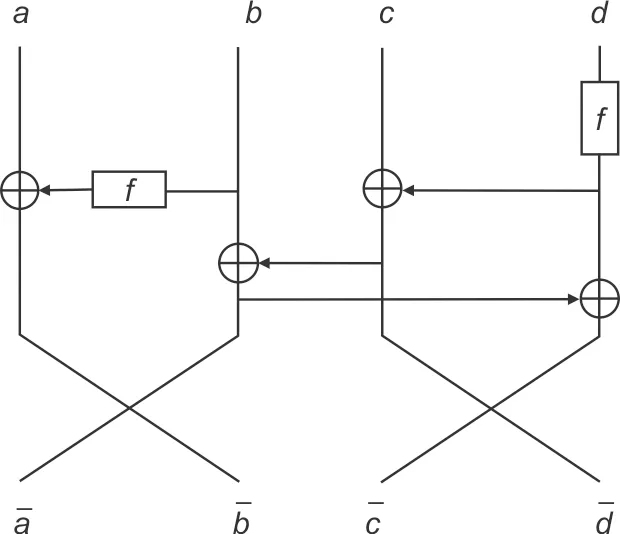
图5 省略轮秘钥的一类4路两重Feistel和R-MISTY结构

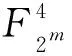
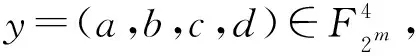
不同于图4的另一类省略轮秘钥的4路两重Feistel和L-MISTY结构如图6所示。

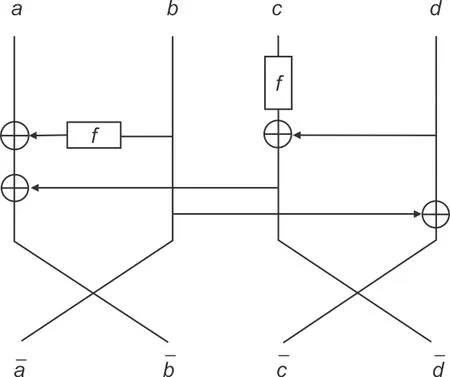
图6 另一类省略轮秘钥的4路两重Feistel和L-MISTY结构

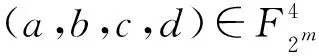
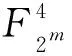
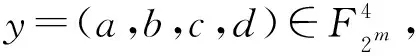
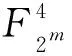
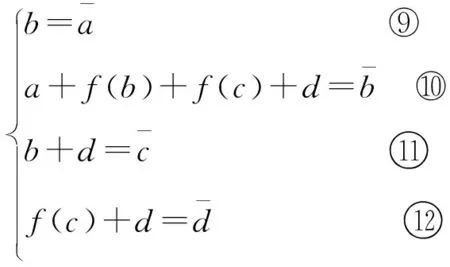
(3)

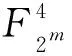
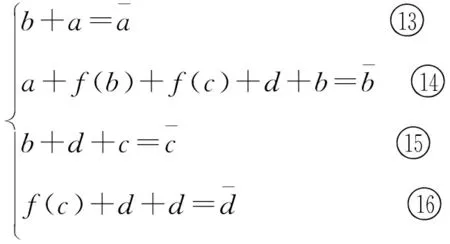
(4)

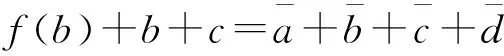
(5)

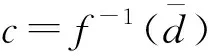
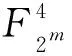
3 总结