浮体自由衰减运动阻尼识别方法误差分析

杨立军，赵 亮，王一听，王 磊，秦立成

(1.上海交通大学 海洋工程国家重点实验室，上海 200240；2.中国舰船研究设计中心，湖北 武汉 430064；3.海洋石油工程股份有限公司，天津 300461)

研究浮式结构物在水中的运动响应，其阻尼主要来自两个方面[1]，分别是辐射运动造波(辐射阻尼)及水黏性影响(黏性阻尼，包括表面摩擦和流动分离引起的涡流)。其中黏性阻尼的量化是浮体水动力学的一个研究热点[2]，对浮式结构物的优化设计具有重要意义。

海上浮式结构物的耐波性研究大多基于势流理论的各种衍生方法[3-6]。使用商业软件[7]或自编程序求解辐射—绕射问题，即可得到浮体的附加质量、线性辐射阻尼和恢复力系数。然而，黏性效应并不能直接通过势流理论得到，往往是在浮体运动控制方程中增加黏性阻尼项以考虑黏性阻尼的影响。基于计算流体力学(CFD)理论的数值水池虽然可以通过相对较低的成本模拟黏性效应[8-9]，但仍需要模型试验提供数据以验证CFD数值模型，因为利用CFD模拟全尺度的黏性流动超出了目前的计算能力。自由衰减试验是模型试验中常用的量化浮体黏性阻尼的手段，其可为基于势流理论的浮体运动方程提供定量的黏性阻尼系数。显然，自由衰减试验的识别结果将直接影响数值模拟的可靠性。

目前，有两种广泛分析自由衰减试验结果以确定辐射阻尼和黏性阻尼的方法：Froude法[10]及Faltinsen法[11]。为确定线性辐射及二阶黏性阻尼系数，Froude法使用了半个周期的自由振荡运动的峰值和谷值，而Faltinsen法则使用每个自由振荡周期的波峰或波谷值。两种方法都依赖于相同的近似，即对于每个持续时间内，用简谐运动近似代替衰减运动。两种方法的主要区别在于Froude法假设每半个周期为正弦运动，且认为运动满足动能守恒，而Faltinsen法则在每个振荡周期内采用等效线性阻尼系数近似代替辐射及黏性阻尼。值得注意的是，由于这些近似假设，这两种方法都为参数识别引入了不确定性。

虽然两种方法在预报非线性阻尼时都存在一定的系统误差，但在精度要求较低或者黏性阻尼较小时，仍有较广泛的应用场景。表1罗列了一些相关具有代表性的研究，可以发现，部分文献中已经基于Froude法和Faltinsen法做出了一些尝试。针对带舭龙骨的FPSO提出双线性分析法(Bi-linear analysis)对其强黏性阻尼表现进行分析。

表1 大型浮式结构物自由衰减试验代表性研究Tab.1 Representative free-decay test studies of large floating structures

由于目前尚未见对阻尼识别方法误差的系统性研究，因此这里研究的目的在于对这两种方法中使用的关键假设所可能引入的误差进行评估，并针对不同阻尼情况下选择何种的识别分析方法提出建议。因此，首先回顾了基本的自由衰变运动方程，重新讨论了Froude方法和Faltinsen方法，并描述了其近似误差，继而提出了直接积分法，尽可能减少由识别方法所引入的误差。最后从数值及试验两个方面评估、分析和讨论了由Froude法、Faltinsen法及直接积分法所引起的误差。

1 自由衰减运动阻尼识别方法

忽略其他运动模态的耦合作用，根据牛顿第二定律，某运动模态下的自由衰减运动方程可被描述为：

(1)

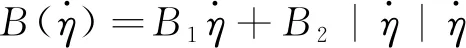
(2)

其中，B1是一阶线性辐射阻尼系数，B2是二阶非线性黏性阻尼系数。故整理可得自由衰减运动一般方程为：

(3)

其中，p1、p2分别是一阶阻尼系数、二阶阻尼系数，ω为自由衰减频率，即固有频率。具体写为：

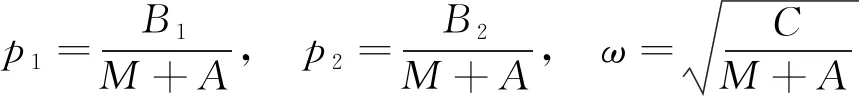
(4)

(5)

(6)

显然，整个自由衰减周期可以分为多个a至b的时间段，对第j个时间段，式(6)可以进一步写成：

p1+αjp2=ω2βj

(7)

其中，

(8)

1.1 Froude法

在Froude法中，时间段a至b被固定为半个周期[21-22]，并假设半个周期内自由衰减运动近似为简谐运动。位移η可以表示为：

η=ηjcos(ωt+φ)

(9)

其中，ηj是间歇运动的幅值，φ则是运动相位。对于第j个半周期自由衰减运动，根据式(8)易得：

(10)

其中，δη为半个周期内峰值谷值幅值之差，ηm则为幅值的平均值。由于简谐运动假设，ηj=ηm，式(7)可最终写成：

(11)

以上即是经典的Froude法线性拟合形式。可见，Froude法的误差来源于简谐近似，其误差可以表示为：

(12)

(13)

其中，εj和φj是Froude法中的相对中间误差。

1.2 Faltinsen法

Faltinsen法在形式上与Froude法不同，但其核心思想是一致的。其将式(3)中的线性阻尼力项和非线性阻尼力项等效线性化成如式(14)所示形式：

(14)

其中，pe是等效线性阻尼系数。根据洛伦兹原理[23]，非线性力所做的功与等效线性力所做的功相同，非线性阻尼部分线性化即可写成：

(15)

这里引入假设，等效线性阻尼系数pe在一个自由振荡周期内为常数，则结合式(3)与式(14)，位移η的解析解为：

(16)

其中，等效阻尼比ζe=pe/(2ω)，故对于第k个周期，pe及式(7)可以表示为：

(17)

(18)

其中，ηj和ηj+1为周期j中的两个峰值(或谷值)。与Froude法类似，Faltinsen法的误差也可以表示成：

(19)

(20)

其中，εj和φj是Faltinsen法中的相对中间误差。

1.3 直接积分法

通过回顾Froude法和Faltinsen法，其所引入假设可分为3部分：1) 阻尼力的二阶多项式假设；2) 线性和二次阻尼系数的常数假设；3) 简谐运动假设。其中假设3)的简谐运动假设并不能完全反映实际衰减运动，所以文中摒弃假设3)，基于假设1)和2)，提出一种直接积分方法，以便在识别线性、二次阻尼系数时给出更可靠结果。

1) 以式(16)为目标函数，基于试验数据，展开非线性拟合，并采用归一化均方根误差NRMSE来估计测量数据和拟合数据之间的接近度[24]：

(21)

其中，mi是试验测量的第i个数据，fi是拟合结果的第i个数据，mmax和mmin是试验测量的最大值和最小值。由公式可知，NRMSE的数值范围为[0，1]，且越接近0表示拟合数据越接近测量数据。由于式(16)存在4个未知变量，故在保证拟合精度条件下，在非线性拟合中需保持初始位移和最终位移一致(如图1所示)。

图1 垂荡自由衰减模型试验第一和第五周期的非线性拟合结果[25]Fig.1 Nonlinear fitting results for a heave free-decay model test:1st and 5th cycles[25]

2) 一旦式(16)中的主要系数(ζe、ω、c1和c2)通过非线性拟合获得，速度公式即可通过式(16)求导得到，即：

(22)

3) 根据式(22)，进而计算式(8)中α和β的数值积分，得到图2所示的线性回归结果，对应的p1=0，p2=8.68。以上即为基于直接积分法得到的一阶阻尼系数和二阶阻尼系数。

图2 垂荡自由衰减试验的线性回归结果Fig.2 Linear regression results for a heave free-decay test

2 数值及试验研究结果与讨论

2.1 数值研究

文中的数值研究对象为某大型浮式结构物[25]，采用式(3)的数值解来估计近似误差，表2列出了算例中求解式(3)的主要参数。式(3)的求解采用4阶Runge-Kutta方法，自由衰减运动位移η由MATLAB中的ODE45求解器计算得出。相对和绝对误差分别为1×10-3和1×10-5。分别对中间过程误差和最终误差进行评估和讨论。中间过程误差分析中，二次阻尼系数p2=10 m-1为常数，以此估计Froude法与Faltisen法所造成的中间过程误差。最终结果误差分析中则采用不同的二次阻尼系数来显示这三种方法的差异。

表2 数值模型的主要参数(垂荡模态)Tab.2 Major parameters of the numerical model for heave mode

2.2 中间过程误差

图3展示了式(3)在随机噪声下垂荡自由衰减运动方程的数值解。使用Froude法和Faltinsen法分别通过截取多组半个周期和一个周期，测得峰值(谷值)，由式(10)和式(17)分别计算得到α和β值，进而根据式(12)、(13)与式(19)、(20)分别得到两种方法的中间误差ε和φ。

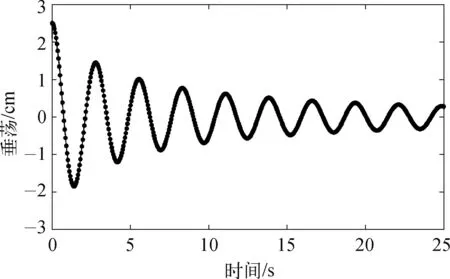
图3 随机噪声下垂荡自由衰减运动方程的数值解Fig.3 Numerical solution to the heave free-decay motion equation with random noises

图4和图5分别显示了无量纲等效线性阻尼系数ζe与Faltinsen法和Froude法对应的每一个全周期和半周期变化。对于整个周期，Froude法采用了峰间周期和谷间周期；对于半周期，Froude法采用了向上运动的峰到谷周期和向下运动的谷到峰周期。图6和图7表明误差ε以及φ是随着ζe增大而增大，且φ远远超过ε，在Faltinsen法中最大的φ达到4.0%左右。Faltinsen法的相对误差ε与Froude法中基本一致。在当前条件下，Faltinsen法的误差ε以及φ明显大于Froude法(最多2.0%左右)。若ζe持续增大，如文献[14]中等效线性阻尼系数为0.15时，误差ε及φ急剧增大达到10%，此时的识别误差将极大地影响最终的识别结果。

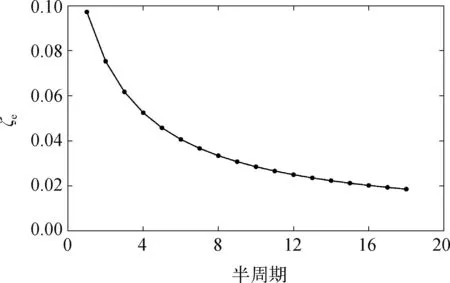
图4 等效线性阻尼系数随半周期变化Fig.4 Equivalent linear damping ratio changing with the entire cycles

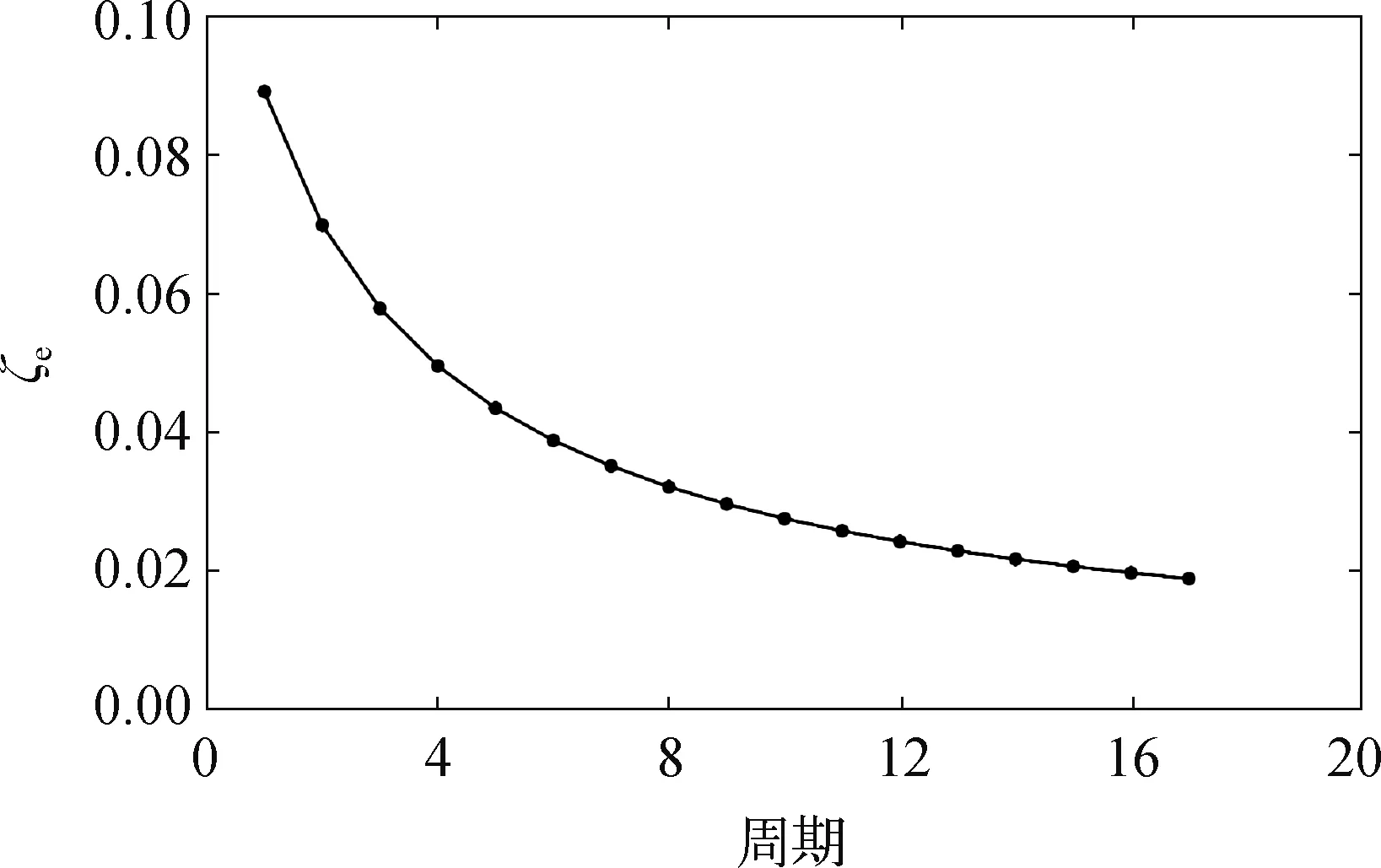
图5 等效线性阻尼系数随周期变化Fig.5 Equivalent linear damping ratio changing with the half cycles

图6 Froude法中ε和φ与等效线性阻尼比ζe的关系Fig.6 Relationship of ε and φ with the equivalent linear damping ratio ζein Faltinsen method

图7 Faltinsen方法中ε和φ与等效线性阻尼系数ζe的关系Fig.7 Relationship of ε and φ with the equivalent linear damping ratio ζein Froude method

2.3 最终结果误差

为了揭示Froude法、Faltinsen法和直接积分法线性回归拟合结果的差异，采用了不同的二阶阻尼系数来比较其最终拟合结果误差，p2范围从0到25 m-1。其他主要参数见表2。图8显示了式(4)在不同二阶阻尼系数下的垂荡运动位移，图9和图10显示了采用Faltinsen法、Froude法和直接积分法得到的线性和二次阻尼系数，表3给出了3种方法下数值拟合结果。

表3 Froude法、Faltinsen法和直接积分法的识别结果Tab.3 Identification results using Faltinsen，Froude and direct integration methods

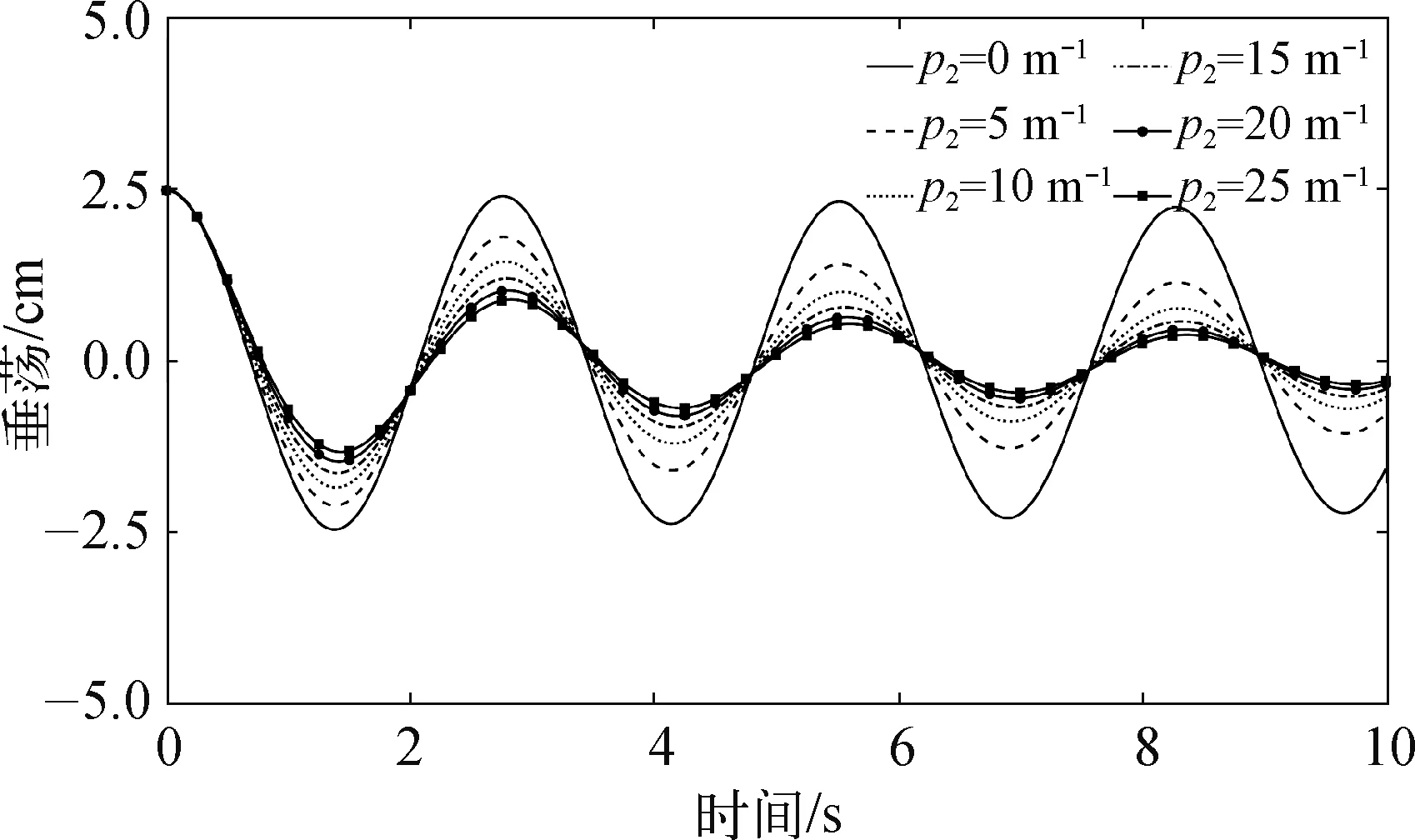
图8 不同二阶阻尼系数影响下的垂荡自由衰减运动Fig.8 Heave free-decay motions with different values of quadratic damping

图9 Froude法、Faltinsen法和直接积分法确定线性阻尼系数p1Fig.9 Linear damping coefficient p1 identified by Faltinsen，Froude and direct integration methods

图10 Froude法、Faltinsen法和直接积分法确定二阶阻尼系数p2Fig.10 Quadratic damping coefficient p2 identified by Faltinsen，Froude and direct integration methods

从数值拟合结果可以看到，Froude法和Faltinsen法的系统误差随着等效阻尼系数ζe的增大而增大，而直接积分与目标值没有差异。随着由0.011增加到0.118，由Faltinsen法引起的p1误差由0增加到68.0%，p2误差从0提高到12.7%。Froude法引起的相对误差较Faltinsen小，分别为从0到32%和5.7%。由于线性和非线性阻尼系数之间巨大的数量级差异，p1相对误差对p2更加敏感。以上的分析讨论是数值算例的具体分析结果，并不具有普遍性。线性和二阶阻尼系数之间数量级的差异导致了其在评估最终系统误差时出现不同的误差结果。

2.4 试验研究

试验研究是基于某大型浮式结构物垂荡衰减运动试验[25]所展开的，试验如图11所示。原始数据和光滑处理后的数据如图12所示，采用不同识别方法的阻尼系数识别结果如图13所示。

图11 自由衰减试验Fig.11 Snapshot of an experimental free-decay case

图12 垂荡自由衰减位移时历Fig.12 Experimental heave free-decay displacement

由图13可知，Faltinsen法、Froude法和直接积分法所识别的线性及非线性阻尼系数p1和p2有着明显的区别。可以看到，每种方法中的等效线性阻尼系数pe有着较大的振荡，这可能是由恒定非线性阻尼假设、测量误差和随机白噪声引起的。Faltinsen法中的二阶阻尼系数p2与直接积分法之间的偏差比Froude方法要大，这与数值研究的结论一致。相反，由Faltinsen法得到的线性阻尼系数p1与直接积分法所得到的结果具有良好的一致性。从图13可以看到，这些阻尼识别方法对数据都较为敏感，原始试验数据的较小干扰可能会导致最终结果的大偏差。因此，为了尽可能地提高识别结果的准确性，需要大量的试验数据。然而，在实际情况下，试验资源相对有限，数据往往不足以支撑采用Froude法或者Faltinsen法获得可靠的试验结果。从这个角度来看，对于具有强非线性阻尼的浮体，采用半周期的直接积分法具有更好的准确性。

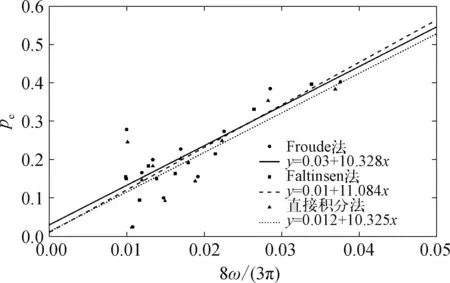
图13 不同方法对线性和二阶阻尼系数试验识别结果Fig.13 Identification results of the linear and quadratic damping experimental results using different methods

3 结 语

对经典的Froude法和Faltinsen法进行了回顾，明确了这两种方法中的简谐运动假设是在强非线性阻尼情况下获取线性和非线性阻尼系数的误差主要来源之一。文中量化了Froude法和Faltinsen法的系统误差，并提出了直接积分法。建议针对具有强非线性阻尼的浮体，当需要较高精度时，采用直接积分法识别阻尼系数，这具有较高的准确性。从数值和试验研究的角度，对Froude法和Faltinsen法所引入的中间过程误差和最终结果误差进行了分析与讨论。试验结果也表明Faltinsen法、Froude法和直接积分法在识别阻尼系数时存在差异。具体结论如下：

1) 半周期假设下的Froude法对线性阻尼系数和二次阻尼系数的预报均优于单周期假设下的Faltinsen法。

2) 线性阻尼系数p1比二阶阻尼系数p2更对数据敏感，由于数值研究中的p1、p2量级差异较大，p1的识别误差明显大于p2。

3) 直接积分法与目标值基本一致，适用于大阻尼、高精度要求的情况。同时也可以注意到，Faltinsen法和Froude法在处理小非线性阻尼情况时，具有数据处理速度快、精度相对较高等优点。它们适用于没有小型构件的船舶和海洋结构物，而这些构件可能会引入较强的黏性阻尼。