基于FLUENT的波浪溢流水动力数值模拟
黄飞扬,戴文鸿,姚 毓,陈羿名
(河海大学 水利水电学院,江苏 南京 210098)
波浪溢流[1]是指沿海地区极端高水位和热带气旋增加产生的风暴潮导致海堤堤前水位超过堤顶,海堤受到越浪与溢流联合作用的现象[2]。在全球气候变暖的背景下,极端气候事件发生的强度和频率都在不断增加[3],这使得发生波浪溢流现象的概率也进一步提高。波浪溢流一旦发生,将会极易引起大规模的溃堤灾难[4]。2005年卡特里娜飓风风暴潮期间,美国墨西哥湾沿岸由于波浪溢流产生的海堤后坡侵蚀破坏就多达43处[5],大量的村庄和农田被海水冲毁。自此波浪溢流现象受到了海岸工程界学者的高度重视,波浪溢流也成为了海堤设计和安全评估中必须考虑的因素。
自2005年卡特里娜飓风以来,波浪溢流产生的溃坝溃堤灾害受到了整个海岸工程界的高度关注,国内外学者也对此做了大量的研究。如欧洲的越浪手册(第一版)[6]、Reeve等[7]、Hughes等[8]和Li等[9]都围绕着波浪溢流越堤流量参数对其水动力特征进行了分析计算,然而上述研究仅仅较为宏观地反映出海堤对波浪溢流水动力特征的影响,对越堤水流的形态、空间变化的相关描述却极为缺乏。为了进一步研究波浪溢流对海堤不同时间、空间分区的影响,可以通过使用计算流体软件对海堤各重要位置的水动力特征进行模拟。随着计算机技术发展,基于FLUENT软件模拟达到工程实用水平的数值波浪水槽已经成为了国际海岸与近海工程界关注的热点。如周勤俊等[10]利用FLUENT软件将模拟的入射波作为人工分布源项加入动量方程之中,发展得到了适用于流体体积(VOF)方法的源项造波法;黄华等[11]针对波浪及其影响效应的研究需求,采用了推波板造波方法对典型二维Stokes波产生、发展和消亡过程进行了准确的仿真研究;徐刚等[12]通过在入口处添加速度场来模拟波浪在受数值因素影响下所造成的衰减,并得到数值仿真精度更高的模拟方案。通过上述研究,针对波浪溢流水动力变化过程的特点,将采用UDF速度边界造波方法对规则波中的二阶Stokes波进行模拟。该方法主要通过对入口水质点输入自定义速度获得相应的波浪波形,经验证输出的波形较其他方法十分准确,同时模型计算量急剧减小,使得数值仿真精度和效率都得到了一定的提高[13-14]。阻尼消波法主要对波浪遇建筑物时的消波效果较好[15],同实验室的消波方法原理相同,加入阻尼源项后,便于对阻尼消波区域进行控制,使得参数设置更加方便。因此,为了防止波形受到海堤反射的作用,可采用阻尼消波方法消除反射波对波浪溢流水动力特性的影响。
综上所述,将使用UDF速度边界造波和阻尼消波法对不同超高和波浪要素的波浪溢流现象进行模拟。将模拟结果与Hughes等[8]和Li等[9]物理模型试验相关研究成果进行对比验证分析,并对波浪溢流中越浪和溢流的主导性关系进行探讨。再进一步通过各测点水动力变化的时间序列研究海堤后坡水流厚度的动态过程,同时对海堤后坡稳定水深公式进行拟合并验证。
1 数学模型
1.1 基本控制方程和湍流模型
在对波浪溢流进行模拟时,研究的二维波浪属于不可压缩黏性流体,即将流动视为包含水和空气的两相流进行处理,空气和水的交界面即为模拟波浪的波面,且二者之间不可渗透。这里取水平方向为x轴(向右为正),取垂直方向为y轴(向上为正)。因此得到的N-S(Navier-Stokes)控制方程可简化为:
连续方程的表达式为:
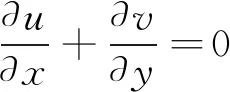
(1)
动量方程的表达式为:

(2)
式中:u和v分别表示为在两个方向(x、y方向)上速度的分量;P为流体微元体上的压力;ρ为流体密度;ν为流体动力黏度系数。
当波浪接近海堤时,由于海堤坡度的影响使得水流产生较大的紊动甚至导致波浪破碎,因此在波浪溢流数值水槽建立之前应对湍流模型进行考虑。RNG k-ε模型是由标准的k-ε模型改进而来,最早由Yakhot等[16]提出,该模型考虑了大面积流体运动和空间位置变化的同时还可以捕捉到流线弯曲程度较大的流动,十分适合对波浪溢流和海堤相互作用的模拟。其湍流模型数学表达式为:

(3)
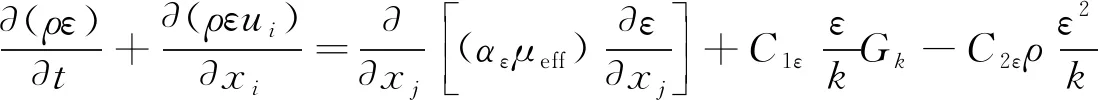
(4)
其中,
μeff=μ+μt
(5)
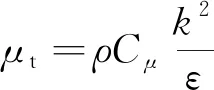
(6)
式中:Gk由平均速度梯度引起的湍动能产生;αk和αε分别为湍流能和耗散率有效普朗特数的倒数;C1ε和C2ε为经验参数,取默认值分别为1.42和1.68;由于文中流体运动的雷诺数较大(Re>30 000),故Cμ取为0.084 5;μeff为湍流流动时的名义黏性系数;μ为水体的分子黏性系数;μt为湍流黏性系数,即名义黏性系数。模型糙率的选择将参照Hughes等[8]物理模型,因Hughes模型中海堤模型表面为碾压混凝土,其曼宁系数n为0.018,通过FLUENT手册对模型糙率参数进行换算,在FLUENT模型中需要输入的粗糙度常数参数Cs取为0.53。
1.2 VOF方法
在基于N-S方程建立的数值水槽中,能够准确捕捉自由表面的大变形运动是关键。VOF方法适用于有清晰相界面的水体流动,对于处理具有复杂自由表面的波浪溢流问题十分理想,可以清晰地分析出波浪溢流作用于海堤时的冲击压力和流场特征。
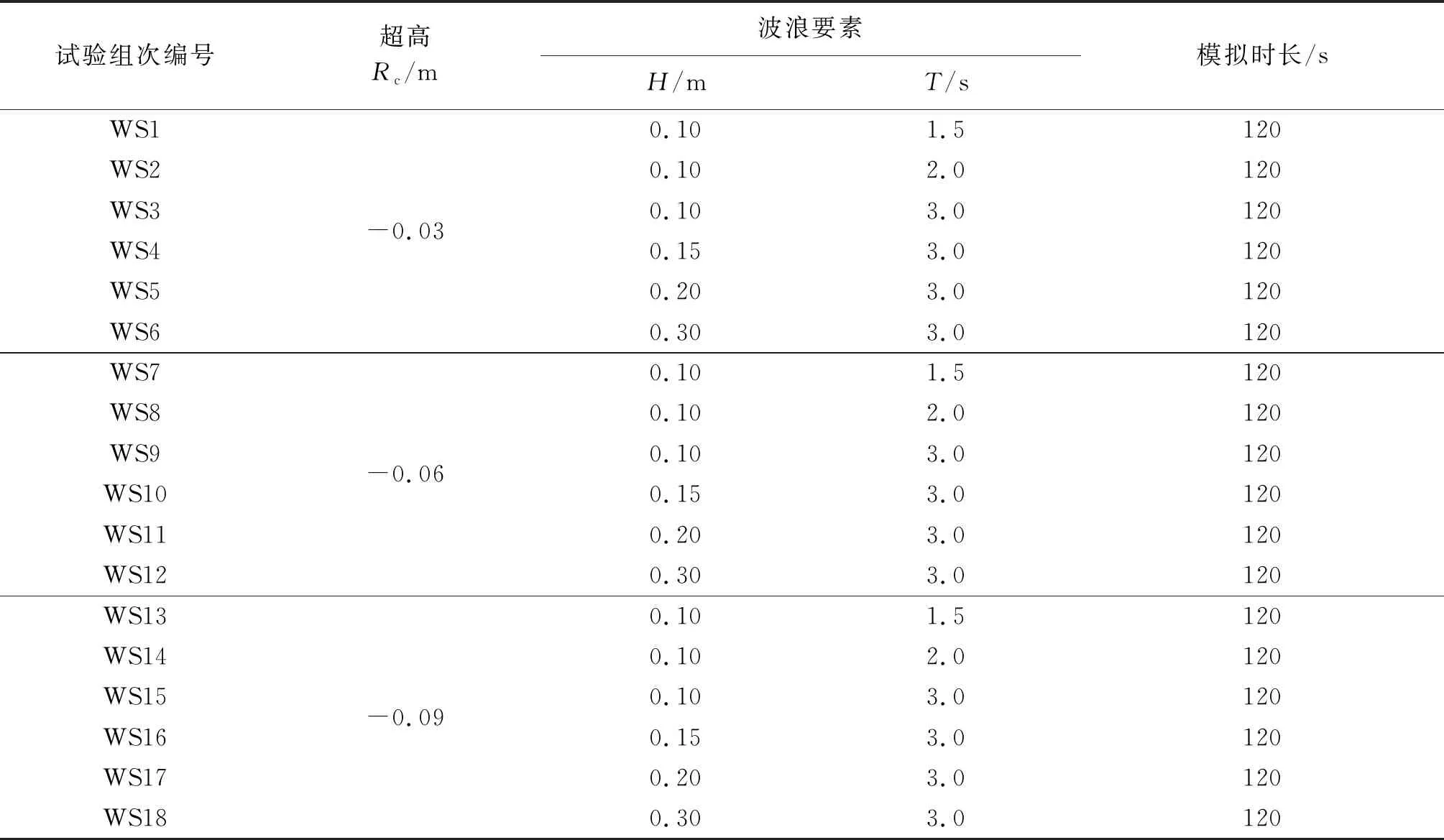
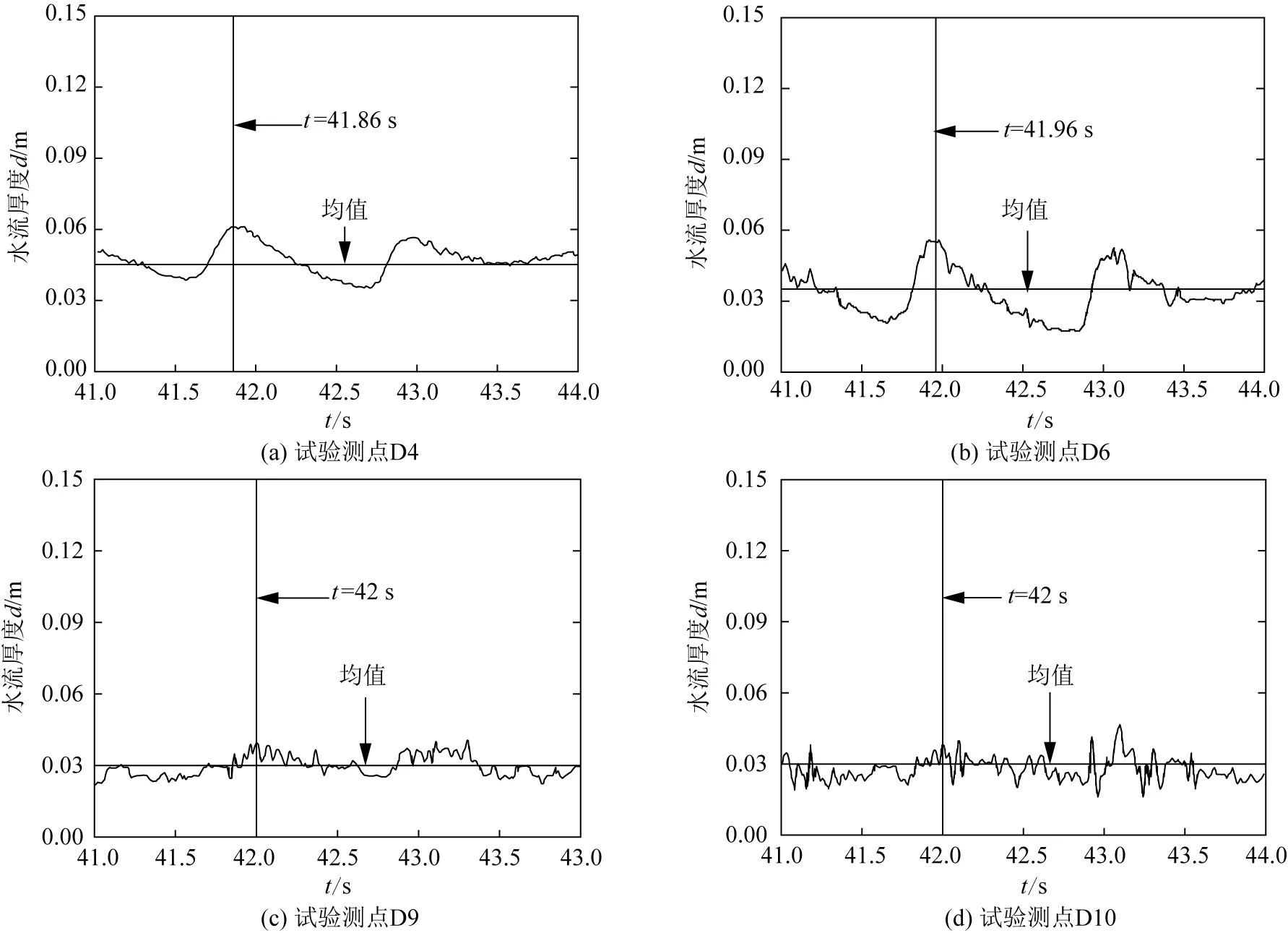
在VOF方法中引入了体积函数aq用于定义第q相流体所占体积与单元体积的比值,则体积函数aq的值存在以下3种可能:若aq=0时,单元中没有第q相流体;若aq=1时,单元中充满了第q相流体;若0 (7) 运用速度边界造波法对规则波中的二阶Stokes波进行数值模拟,速度边界造波法是将入口边界水质点赋予已知的波水平和垂向周期性振荡速度,促使水质点运动产生波浪,并通过波面方程最终确定输入波浪的波形。此方法可以通过FLUENT UDF进行实现。UDF(用户自定义函数)通过用户编制C语言程序连接到FLUENT所提供的预定义宏来实现特有功能,从而达到对软件进行二次开发的目的。利用FLUENT中可以直接访问单元中流体变量的宏DEFINE PROFILE(name,t,i)来定义入口边界水质点的速度方程和波面方程。对于二阶Stokes速度入口边界处的流速分布方程和波面方程可表示为: 波面方程: (8) x方向速度: (9) (10) 式中:ω为波频率;k为波数;H为波高;h为静水位。 波浪和海堤相互作用后,产生的反射波会导致水槽内的波浪特性发生改变,为了消除海堤对波浪的二次反射作用,需要对数值水槽进行消波处理。阻尼消波法是根据实验室水槽消波的原理,在特定的计算区域间加入阻尼源项,起到对该区域间反射波减弱和消除的作用。加入的阻尼源项表达式为: (11) 式中:S为y方向动量方程的源项;C1为线性阻尼常数;C2为二次阻尼常数;V为沿y方向的速度;f(y)为沿y方向的阻尼函数;f(x)为沿x方向的阻尼函数。其中, (12) (13) 式中:xs、xe分别是阻尼层在x方向上的起始位置和终点位置;yfs、ye分别是阻尼层在y方向上的起始位置和终点位置,即自由表面高程和底部高程。 以Hughes等[8]和Li等[9]的大水槽试验为基础,建立了一个与Hughes和Li物理水槽完全相同的二维数值波浪水槽模型。其中模型水槽长49.3 m,高2.80 m;海堤模型高0.65 m,前坡坡度为1∶4.25,后坡坡度为1∶3。在海堤模型前还设置了一个坡度为1∶10、长度为2 m的陡坡,数值波浪水槽和海堤模型如图1所示。 图1 数值波浪溢流水槽示意Fig.1 Diagram of numerical simulation of combined wave and surge overtopping 数值水槽的划分可利用Workbench中的Meshing模块将模型划分为四边形结构性网格,文中主要研究波浪溢流与海堤的作用,需要重点观察海堤表面的水动力特征,则要在海堤模型上加入边界层网格,划分后的全局网格尺寸为0.025 m,边界层网格尺寸为0.010 m。数值水槽的上方设为压力出口边界;底部设为壁面边界;左端为UDF函数输入的速度入口边界;右端有自由出流边界;在海堤前坡位置设置了阻尼消波区。基于上述模型的计算网格和边界条件,将采用有限体积法(FVM)对N-S控制方程和湍流模型进行离散化分析计算,其中选定的时间步长为0.005 s。对于方程中的扩散项采用中心差分格式;对于方程中的对流项,采用二阶迎风差分格式;对于压力和速度的耦合计算,采用压力隐式算子分割(PISO)法进行迭代求解。 文中依据Stokes波浪理论和速度方程对二阶Stokes波进行仿真模拟。在Stokes波浪二阶理论方程中,相对波高H/h(波高与静水深的比值)的使用范围在0.05~0.50之间。因此为了提高模拟的准确性,输入的Stokes波采用了波高H=0.1 m、周期T=1.5 s、超高Rc=0.06 m(即水深为h=0.71 m)的算例,模拟得到的波浪溢流模拟效果如图2(a)所示。为了得到模拟波浪的波形,具体操作如下:在x=10 m处建立体积分数为0.5的监测点,随着波浪的运动,监测其y轴坐标随时间的变化,由其输出的y坐标值便可得到数值波浪水槽造波波形图。计算得到的Stokes波形如图2(b)所示。 图2 Stokes波波形模拟与理论值对比Fig.2 Comparison of experimental and theoretical values of Stokes wave waveform 生成的Stokes波在比较了8个周期数值波浪模拟产生的波形后,发现基本与理论波形吻合,都呈现了“上尖下平”的特点,波浪要素试验值和理论值在各个相位点之间相对误差都小于4%。由以上结果表明该数值波浪水槽对二阶Stokes波的模拟十分准确。 一般检修举措往往会耗费大量的人力、物力、财力,且故障排查不及时,不能消除潜在的安全隐患,往往会造成重大安全事故。而安全有效的带电检测不仅可以大大降低设备损坏的可能性,延长开关柜的使用寿命,而且还能使整个供电系统拥有长期稳定的保障。 波浪溢流可视为越浪和溢流过程的非线性叠加,由此可分析在不同的波浪要素前提下,堤前水位超高对波浪溢流量的影响。具体操作为:在海堤模型上建立10个垂直于水平面的测量面用于测量平均波浪溢流量,其中沿着海堤堤顶等距离建立5个,再沿后坡每隔10 cm建立1个,共建5个,分别命名为Q1~Q10。具体观测面布置如图3所示。 图3 数值模拟流量测量面分布Fig.3 Numerical simulation of flow measurement surface distribution 为了验证数值模拟结果的正确性,选取波浪溢流的基本参数平均波浪溢流量对模型进行验证。分别选取了不同超高Rc和不同波高H的波浪溢流现象进行模拟,其结果与Hughes等[8]和Li等[9]同尺寸物理试验模型的平均波浪溢流量进行比较。结果如图4所示,图中横坐标为无量纲的相对超高,纵坐标为无量纲波浪溢流量。 图4 数值模拟和物理模型实测越堤流量结果比较Fig.4 Comparison of numerical simulation and physical model measured discharge 由图4可知,波浪溢流量模拟结果与Hughes等[8]和Li等[9]的物理试验结果在总体趋势上十分接近,无量纲波浪溢流量随着相对超高的增大不断减小。但在超高相同的条件下数值模拟的平均波浪溢流量都相较于物理试验结果偏小,造成这个现象的主要原因是物理试验中流量测量方法和模型试验条件的不同,从而导致了波浪溢流量的差异。在Hughes等[8]试验模型中波浪溢流量主要通过ADV流速仪和波高仪对海堤后坡的流速与水流厚度进行测量,再通过流量和流速、水流厚度的数值关系计算波浪溢流量。但当小超高的条件下波浪溢流掺混着空气导致水流厚度变大,从而导致波浪溢流量的测量值相较于真实值偏大。而Li等[9]在测量波浪溢流量时虽然改进了上述方法,采用了称重法对波浪溢流量进行测量,但其海堤模型使用普通混凝土进行制作,表面糙率较小,所以波浪溢流量也与数值波浪模拟值相比偏大。但是总体上数值模拟结果和二者试验数据相差不大,通过数值模拟结果与Hughes波浪溢流计算公式进行比较,发现数值模拟结果数据的决定系数R2为0.988,均方根误差RMSE为0.044,由此可以认为波浪溢流数值水槽模型可以准确地模拟出波浪溢流现象。 对图4进行观察可以发现无量纲波浪溢流量随相对超高增大而减小,呈现单调性关系,为了探究无量纲波浪溢流量与相对超高之间的关系,通过Hughes等[8]波浪溢流物理试验数据和Pan等[17]后坡护坡为高性能加筋草的波浪溢流物理试验数据建立了如图5(a)所示的指数关系曲线。其中由Hughes和Pan二者计算波浪溢流量曲线的表达式可以发现在无量纲波浪溢流量与相对超高在Rc/H≤-0.3的范围内试验数据与拟合曲线存在较好的相关性,而在-0.3 为了进一步研究稳定溢流量与波浪溢流量之间的一般规律,首先使用Kindsvater纯溢流量计算公式计算与波浪溢流数值模拟试验组次同等海堤超高Rc下的稳定溢流量qs的数值(计算时摩阻经验参数Cf取为0.544 5,同数值模型的摩阻经验参数相同),然后以数值模拟的波浪溢流量qws和同等海堤超高Rc下对应的稳定溢流量qs的比值qws/qs为纵坐标,以海堤相对超高Rc/H为横坐标绘制图5(b)。 图5 波浪溢流量中波浪与溢流主导性关系Fig.5 Dominant relationship between wave and overflow in combined wave and surge overtopping 由图5(b)可知,当海堤相对超高Rc/H绝对值较大时,比值qws/qs趋近于1,即波浪溢流量接近对应的稳定溢流量,此时波浪溢流过程中溢流占据主导作用,波浪溢流与纯溢流相似,相对超高与波浪溢流量之间主要呈现为指数关系;当海堤相对超高Rc/H绝对值趋近于0时,比值qws/qs迅速增大,波浪溢流量达到对应稳定溢流量的数倍,此时波浪溢流过程中越浪逐渐占据主导作用,由于越浪量主要满足韦伯分布,打破了波浪溢流量与相对超高之间较为稳定的指数关系,从而使得波浪溢流量随着相对超高的增加逐渐表现为随机性,使用Hughes和Pan的指数函数公式计算平均波浪溢流量将不再准确。这种误差以Rc/H=-0.3为明显的分界点,这解释了图5(a)所示的波浪溢流量在Rc/H=-0.3两侧表现出不同的分布趋势的原因。因此,可以以Rc/H=-0.3为界,将Rc/H≤-0.3的波浪溢流称为溢流主导的波浪溢流,将-0.3 在对波浪溢流主导性作用研究中发现,波浪溢流越过堤顶后,当底摩阻、紊动等产生的摩阻比降与坡度相同时,后坡水深从脉动运动逐渐达到相对稳定的状态。为了进一步研究波浪溢流水力学参数后坡稳定水深变化情况,可以利用FLUENT中监测功能沿海堤模型表面定义10个流速测量点(D1~D10),各个测点与流量测量面Q1~Q10处于同一水平位置。通过流量—流速—水流厚度之间的关系近似得到该测点的水流厚度。选择3种不同超高的模拟工况对后坡水流厚度进行研究,具体模拟组次安排如表1所示。 表1 模拟试验组次Tab.1 Test groups 由水力学基本理论可知波浪溢流发生后,波浪溢流由堤顶流向后坡的过程中当摩阻比降和坡度相等时,水流流速和厚度不再变化并达到后坡平均稳定水流厚度dsm。为了准确了解后坡水流状态随时间的变化情况,选取上述Rc=-0.06 m的模拟组次WS7,对后坡D4、D6、D9、D10处水流厚度结果进行分析,其中D4位于堤顶,D6测点位于后坡上段,D9和D10测点位于后坡下段(具体位置分布见图3)。其模拟结果如图6所示。 如图6所示,当水流在D4、D6处时,水流厚度呈现大波动形态,尤其D6处于堤顶与后坡的交界位置,受结构突变的影响,水流厚度变化十分剧烈。随着时间推移波浪溢流非恒定水流峰值也在不断的向后移动,产生如此现象的主要原因是受到了波浪运动的影响导致堤顶和后坡上端水流产生巨大紊动,峰值在后堤向下周期性运动,水流状态十分不稳定;随着水流运动后移到达后坡下段D9、D10处时,相同时间节点下(t=42 s)二者的平均水流厚度相同,此时水流受后坡阻力的影响,水位渐渐处于稳定,呈现为多峰小波动状态。其中后坡流速不断提高,导致后坡下端水流厚度小于堤前水位,最终平均水流厚度逐渐趋向稳定,达到后坡平均稳定水流厚度dsm。 图6 试验4个测点处Rc=-0.06 m时水流厚度d随时间变化Fig.6 Variation of flow thickness d with time at Rc=-0.06 m at four test points 根据表1提供的不同模拟工况,测量计算各个测点(D1~D10)水流厚度平均值dm沿着堤顶后坡的变化情况,并与相同超高条件下的纯溢流平均水流厚度进行比较,比较结果如图7所示。 由图7可知,当超高Rc较大时,波浪溢流作用下海堤堤顶和后坡的平均水流厚度dm相较于纯溢流偏大,随着超高的减小,平均水流厚度dm将趋近纯溢流作用下沿海堤堤顶和后坡的水流厚度。这主要是因为当超高较大时,波浪溢流越堤流量受波浪影响较大,波浪对波浪溢流量的影响占据主导地位,产生了涨水效果并有一定的越浪量,因此平均水流厚度较大。随着超高Rc的减小,波浪影响减弱,平均波浪溢流越堤流量逐渐接近纯溢流量。当相同超高条件下,不同组次的平均水流厚度沿着后坡逐渐减小并接近,这主要是因为波浪作用范围主要在堤顶和后坡上端,而后坡下端受波浪影响较小,从而水流状态逐渐稳定类似于纯溢流。越堤水流在由堤顶流向后坡的过程中水流厚度逐渐减小,水流流速逐渐增大,当因底摩阻、紊动等产生的摩阻比降和坡度相等时,平均水流厚度和水流流速不再发生变化,此时的水流厚度达到后坡平均稳定水流厚度dsm。 图7 平均水流水深dm沿堤顶后坡的变化Fig.7 Variation of average flow velocity along the dike 为了探究平均稳定水流厚度dsm估算方法,经过与不同特征参数进行组合分析,建立无量纲化后坡平均稳定水流厚度dsm/H与无量纲化平均波浪溢流越堤流量qws/(gH3)1/2之间的相关关系,结果如图8所示。 图8 无量纲化后坡平均稳定水流厚度dsm/H与平均波浪溢流越堤流量qws/(gH3)1/2关系Fig.8 Relationship between average steady flow thickness and average combined wave and surge overtopping discharge 图8中的拟合曲线可表示为: (14) 式中:dsm为波浪溢流平均稳定水流厚度,qws为平均波浪溢流越堤流量。上述公式的适用范围为-0.9 在运用FLUENT软件的基础上,建立了自定义的UDF速度边界函数进行造波,以VOF方法为基础加入了RANS控制方程进行离散求解。验证了数值波浪溢流水槽造波和消波的正确性,完整的模拟了波浪溢流的生成、传播以及与海堤相互作用的过程。根据此模型研究了波浪溢流发生后波浪溢流主导性问题和海堤后坡水流厚度等内容,得出了如下结论: 1)对波浪溢流的主导性进行定义,以Rc/H=-0.3为界,将Rc/H≤-0.3的波浪溢流称为溢流主导的波浪溢流,将-0.3 2)由于受到了波浪运动的影响,导致堤顶和后坡上端水流产生巨大紊动,水体厚度峰值在后堤向下周期性运动,导致波浪溢流非恒定水流峰值随着时间不断后移,当到达后坡下段D9、D10处时,相同时间节点下平均水流厚度趋近一致,最终达到后坡平均稳定水流厚度dsm。 3)以结论2)为基础,对不同特征参数进行组合分析,建立无量纲化后坡平均稳定水流厚度dsm/H与无量纲化平均波浪溢流越堤流量qws/(gH3)1/2之间的函数关系,得到了波浪溢流后坡稳定水流厚度的计算公式。
1.3 波浪水槽的造波和消波
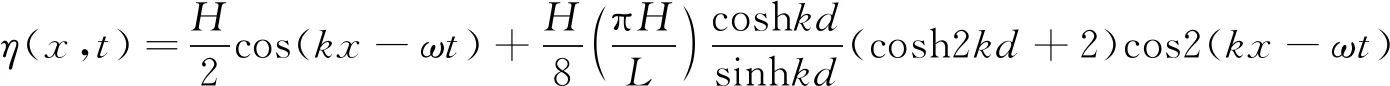
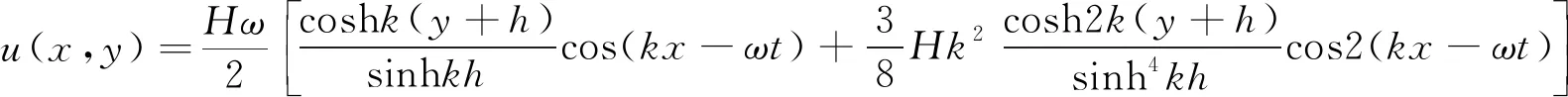




2 波浪溢流水槽的建立与验证
2.1 数值波浪溢流模型和参数设置

2.2 数值波浪水槽的验证



3 模拟结果与分析
3.1 波浪溢流量分析

3.2 波浪溢流后坡水流厚度分析


4 结 语

