BH 分子8 个Λ-S 态和23 个Ω 态光谱性质的理论研究*

邢伟 李胜周 孙金锋 李文涛 朱遵略 刘锋

1) (信阳师范学院物理电子工程学院,信阳 464000)

2) (河南师范大学物理学院,新乡 453000)

3) (潍坊科技学院,寿光 262700)

本文利用内收缩多参考组态相互作用方法计算了BH 分子8 个低电子态(X1Σ+,a3Π,A1Π,b3Σ—,23Π,13Σ+,15Σ—和15Π)和在自旋-轨道耦合效应下所产生的23 个Ω 态的势能曲线、以及和A1Π1态之间6 对跃迁的跃迁偶极矩.为了获得精确的势能曲线,计算中修正了单双电子激发、核价相关效应、相对论效应和基组截断带来的误差.获得的BH 分子的光谱和跃迁数据与现有的理论值和实验值符合得很好.计算结果表明:BH 分子的A1Π1(υ′=0—2,J′=1,+) →(υ′′=0—2,J ′′=1,—)跃迁具有较大的爱因斯坦A 系数和加权的吸收振子强度、高度对角化分布的振动分支比,A1Π1 态具有较短的辐射寿命.另外,a 3Π0+ 和a3Π1 态对A1Π1(υ′=0) ↔(υ′′=0)循环跃迁的影响可以忽略.因此,基于A1Π1(υ′=0—1,J ′=1,+)循环跃迁,我们提出了用一束主冷却激光(λ00=432.45 nm)和两束再泵浦激光(λ10=479.67 nm 和λ21=481.40 nm)冷却BH 分子的方案,并评价了冷却效果.

1 引言

BH 分子在天体物理[1-3]和激光冷却分子[4,5]中起着重要作用.获得BH 分子精确的光谱和跃迁数据对识别太阳光球和太阳黑子中的BH 分子、分析激光冷却BH 分子的可行性和构建激光冷却方案至关重要.

实验上随着光谱技术的发展,科学家们利用气相光谱技术从微波到紫外区域对BH 分子进行高分辨的电子和振动-转动光谱研究[6-14].例如,John 等[6]测量了近紫外区域A1Π ↔ X1Σ+跃迁的0-0,1-0,1-1,2-1,2-2,3-2 和3-3 振转带.Luh 和Stwalley[7]利用实验[6]中的光谱常数和RKR方法构建了X1Σ+,A1Π 和B1Σ+态的势能曲线.Pianalto 等[8]利用傅里叶变换光谱仪记录了X1Σ+态1-0,2-1 和3-2 振转带的红外发射光谱.Douglass等[9]利用激光诱导荧光(LIF)技术观察到A1Π → X1Σ+跃迁的0-1 和1-2 振转带.Fernando 和Bernath[10]利用傅里叶变换光谱记录了433 nm 附近A1Π →X1Σ+跃迁的0-0,1-1 和2-2 振转带.Persico[11]对A1Π态的各种衰减通道进行了相对完整的研究,并推导出X1Σ+态离解能De的最佳实验值.Clark 等[12]利用光子共振增强的多光子电离光谱观察了A1Π→ X1Σ+跃迁的2-0 振转带.Shayesteh 和Ghazizadeh[13]利用获得的X1Σ+态的光谱数据并结合同位素拟合,报道了X1Σ+态的Dunham 系数.Brazier[14]利用发射光谱对b3Σ—→ a3Π 跃迁进行了研究.这些实验集中于研究该分子X1Σ+,A1П,a3П和b3Σ—态的光谱性质,报道了这4 个电子态精确的光谱常数和分子常数、A1П → X1Σ+跃迁的部分数据(Franck-Condon 因子、爱因斯坦A系数Aυ′υ′′和A1П态的辐射寿命τυ′);但未报道考虑自旋-轨道耦合(SOC)后Ω 态的光谱和跃迁数据.

近年来,随着从头计算方法的快速发展,人们对BH 分子基态和激发态电子结构进行了高精度的理论研究[5,15-20].Petsalakis 和Theodorakopoulos[15,16],Miliordos 和Mavridis[17]以及王新强等[18]利用多参考组态相互作用方法(MRCI)结合大的相关一致基组计算了BH 分子一些Λ-S 电子态的势能曲线,并获得了这些电子态的光谱常数.Koput[19]采用多参考平均耦合对泛函(MR-ACPF)方法,结合相关一致核价基确定了X1Σ+态的势能曲线,为了获得可靠的光谱常数,在计算中包含高阶电子相关、标量相对论(SR)效应、绝热和非绝热效应修正.Yan 和Yan[20]纳入SR 效应,采用考虑Davidson修正(+Q)的显关联MRCI(MRCI-F12 +Q+SR)方法对X1Σ+和A1Π 态的电子结构进行了高精度的研究,并报道了势能曲线、光谱常数、振动能级ΔGυ、惯性转动常数Bυ和离心畸变常数-Dυ,A1Π → X1Σ+跃迁数据(Franck-Condon 因子、跃迁能量和A1Π 态的τυ′).Gao 和Gao[5]基于光谱和跃迁特性研究了激光冷却BH 分子的可行性,得到了A1Π → X1Σ+跃迁高度对角化的Franck-Condon 因子.然而,a3Π → X1Σ+是自旋禁阻跃迁,只有在考虑SOC 效应后,a3Π0+和a3Π1态到态的跃迁才可以发生;在他们的研究中未涉及 a3Π0+和a3Π1态对A1Π1↔光学循环的影响.此外,他们在构建BH 分子电子态的势能曲线时没有考虑基组截断误差和相对论(SR 和SOC)效应的影响.因此,本文纳入SR 和SOC 效应、核价相关效应(CV)和外推势能到完全基组(CBS)极限对BH 分子的光谱和跃迁特性进行深入的研究.

2 计算方法

H 原子第一激发态(2Pu)与基态(2Sg)的能级间隔大于B 原子的第一激发态(4Pg)与相应基态(2Pu)的能级间隔.因此,BH 分子前两个离解极限是B(2Pu)+H(2Sg)和B(4Pg)+H(2Sg).利 用Wigner-Witmer 定则,推算出这两个离解极限产生8 个Λ-S 态(X1Σ+,a3Π,A1Π,b3Σ—,23Π,13Σ+,15Σ—和15Π),在SOC 效应的作用下,这8 个Λ-S 态将产生23 个Ω 态.为了探讨电子态之间的相互作用对光谱和跃迁特性的影响,我们对8 个Λ-S 态和23 个Ω 态的电子结构进行了研究.本文在MOLPRO 2010.1 程序包[21]C2v点群中计算BH 分子8 个Λ-S 态、23 个Ω 态的势能曲线和电子态之间的跃迁偶极距.在0.06322—1.04322 nm 的核间距内,首先基于Hartree-Fock(HF SCF)方法处理基态(X1Σ+)的电子波函数,为了描述原子轨道,两个原子都使用相关一致基组aug-cc-pV6Z(AV6Z)[22].然后利用态平均的完全活性空间自洽场(SACASSCF)和内收缩MRCI(icMRCI)方法分别处理静态电子相关和动态电子相关.活性空间包括所有的价轨道(B 原子的2s2p 轨道和H 原子的1s 轨道)和B 原子3s 轨道,即4 个电子在6 个分子轨道上.此外,SA—CASSCF 和icMRCI方法用于计算激发态(a3Π,A1Π,b3Σ—,23Π,13Σ+,15Σ—和15Π)的电子结构.由于icMRCI方法仅考虑了单双电子激发,本文使用Davidson 修正(+Q)[23]估计三阶和四阶电子激发对相关能的贡献.每个电子态的核间距间隔为0.02 nm,为了显示势能曲线的细节信息,在0.10322—0.20122 nm 范围内,核间距间隔为0.002 nm.

为了获得8 个电子态精确的势能曲线,在上述计算的基础上,本文考虑了CV 效应、SR 效应并外推势能到CBS 极限.具体处理方法为:在icMRCI +Q理论水平上使用cc-pCVTZ (CVTZ)基组[24]计算CV.CV 贡献的势能为:ΔEcorr=Ecorr(all-electron)−Ecorr(frozen-core),其中Ecorr(all-electron) 为BH 分子的6 个电子都参与计算获得的相关能,Ecorr(frozen-core)为所有价轨道上的电子参与计算获得的相关能;在icMRCI+Q理论水平上利用包含三阶Douglas-Kroll-Hess (DKH3)[25]近似的cc-pV5Z-DK 基组[26]计算SR 效应.为了消除AV6Z 存在的基组截断误差,本文在icMRCI+Q方法结合AV6Z 和AV5Z基组获得的势能曲线基础上,利用Oyeyemi 等[27]提出的外推公式将这8 个电子态的势能曲线外推至CBS 极限,表示为icMRCI+Q/56;将CV 和SR贡献的势能加到icMRCI+Q/56 势能里,便得到icMRCI+Q/56+CV+SR 理论水平上8 个Λ-S 态的势能曲线,如图1 所示.

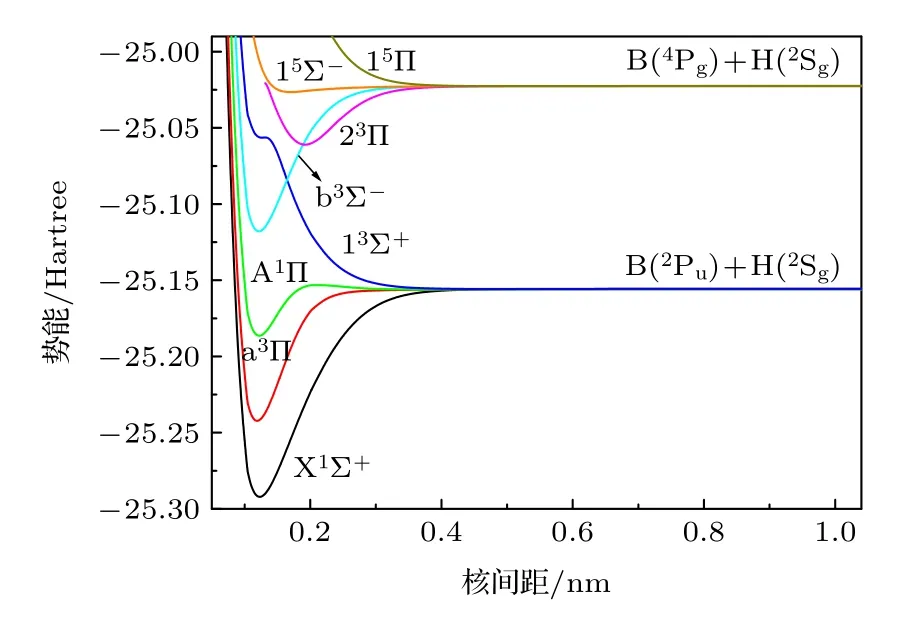
图1 BH 分子8 个Λ-S 态的势能曲线Fig.1.Potential energy curves of 8Λ-S states of the BH molecule.

本文利用icMRCI+Q方法结合全电子CVTZ基组进行SOC 计算.采用带Breit-Pauli SOC 算符[28](HSO)和不带HSO的全电子CVTZ 基组来计算势能.这两种能量的差值即为SOC 效应对总能量的贡献.将SOC 效应贡献的能量加到icMRCI +Q/56+CV+SR 结果的势能中,便得到icMRCI +Q/56+CV+SR+SOC 理论水平上23 个Ω 态精确的势能曲线,如图2 所示.

图2 BH 分子23 个Ω 态的势能曲线Fig.2.Potential energy curves of 23 Ω states of the BH molecule.

基于上述势能曲线,利用LEVEL 8.2 程序[29]求解核运动的振转 Schrödinger 方程,获得 7 个束缚Λ-S 态(X1Σ+,a3Π,A1Π,b3Σ—,23Π,13Σ+和15Σ—)以及17 个束缚和准束缚Ω 态的光谱常数(Te,Re,ωe,ωexe,Be,αe和De)和分子常数;然后,基于,a3Π0+,a3Π1,a3Π2和 A1Π1态的势能曲线和icMRCI/AV6Z+SOC 理论水平的跃迁偶极距,获得这5 个Ω 态之间跃迁的 Franck-Condon因子和Aυ′υ′′.由于振动分支比(Rυ′υ′′)决定了不同电子振动态之间跃迁光子损失路径的相对强度、振子强度决定了跃迁体系吸收或发射的能力、并且天文学家通常使用吸收振子强度 (fυ′J′←υ′′J′′)和加权的吸收振子强度gfυ′J′←υ′′J′′,所以将计算这 5 个 Ω 态之间跃迁的Rυ′υ′′,fυ′J′←υ′′J′′和gfυ′J′←υ′′J′′.最后,计算激 发Ω 态(a3Π0+,a3Π1和A1Π1)的τυ′以及A1Π1(υ′=0,J′=1,+) ↔(υ′′=0,J′′=1,—)跃迁的多普勒温度(TDoppler)和回弹温度(TRecoil).

3 结果与讨论

3.1 7 个Λ-S 态的光谱常数

icMRCI+Q/56+CV+SR 理论水平上计算的Λ-S 态的离解关系列于表1.由表1 可知,本文结果与实验估计值[30]和理论[31]符合非常好,因此本文利用的方法很好地描述了BH 分子的解离情况.

表1 BH 分子前两个离解极限产生的8 个Λ-S 态的离解关系Table 1.Dissociation relationships of the 8 Λ—S states generated from the first two dissociation asymptotes of the BH molecule.

由图1 可知,X1Σ+,a3Π,A1Π,13Σ+,b3Σ—,23Π 和15Σ—为束缚态,15Π 态为排斥态.为方便讨论,表2 列出了本文计算的7 个束缚Λ-S 态光谱常数、挑选的实验值[7,8,10-14]和其它理论值[5,15-20].

X1Σ+态在Re处的主要电子组态为1σ22σ23σ21π04σ05σ0(0.8995),小括号里为组态波函系数的平方.它的势阱深度为29954.56 cm—1,包含22 个振动态.由表2 可知,本文计算的Re,ωe,Be和De与实验值[8,10,12,13]吻合,它们与实验值[8,10,12,13]的最大偏离分别为0.00027 nm (0.219%),2.62 cm—1(0.1108%),0.014 cm—1(0.1164%)和 0.0661 eV(1.8122%);仅文献[15-19]中的Re值和文献[5,15,17-20]中的De值分别比本文的计算值稍微接近实验值[8,13]和实验值[11].

第一激发态a3Π 和第二激发态A1Π 通过3σ →1π 的单电子激发形成,它们在各自Re处的主要电子组 态分别 为1σ22σ23σ11π14σ05σ0(0.9413)和1σ22σ23σ11π14σ05σ0(0.9129).a3Π 态的势阱深度为18961.07 cm—1,包含12 个振动态.A1Π 态在R=0.21289 nm 附近出现势垒,势垒顶部的势能高于无穷远处的势能,势阱深度为7342.74 cm—1,包含4 个振动态,这与实验[12]和理论[16]的结论相同.由表2 知,本文计算的这两个态的光谱常数与实验值[7,10-12,14]吻合很好.

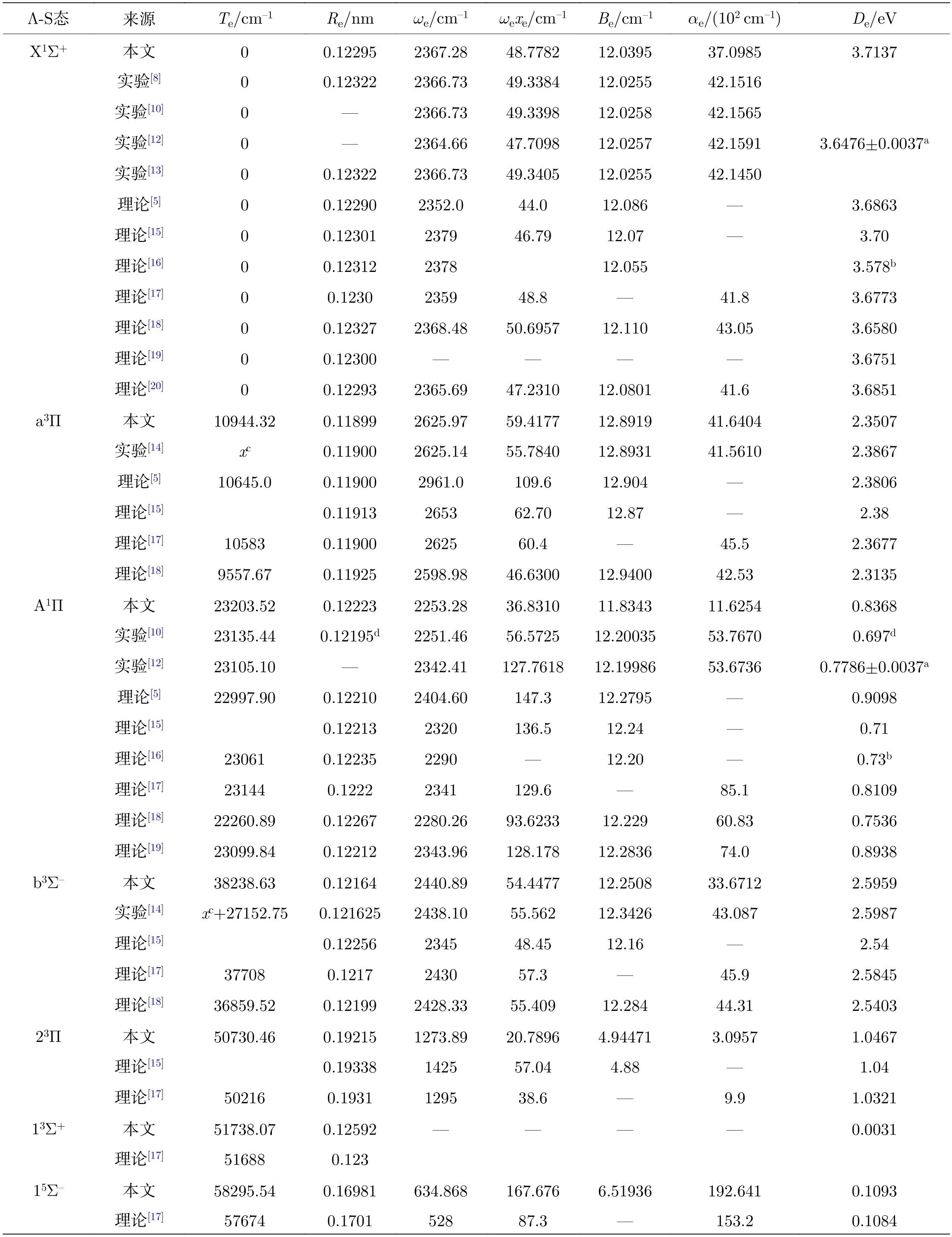
表2 icMRCI+Q/56+CV+SR 理论水平上BH 分子7 个Λ-S 态的光谱常数Table 2.Spectroscopic parameters of the 7 Λ-S states of BH at level of icMRCI+Q/56+CV+SR.

第三激发态b3Σ—态通过3σ → 1π 的双电子激发形成,其在Re处的主要电子组态为1σ22σ23σ01π24σ05σ0(0.8939).b3Σ—态的势阱深度为20938.32 cm—1,包含14 个振动态,它与13Σ+态的排斥部分在R=0.16467 nm 处交叉,计算表明b3Σ—态的预解离始于υ′=2,J′=11 能级.

13Σ+态由3σ → 4σ 的单电子激发形成,其在Re处的主要电子组态为2σ23σ11π04σ15σ0(0.8001),并在R=0.13122 nm 附近出现势垒,势垒高于无穷远处,局域势阱深度为24.80 cm—1,不包含任何振动态.本文的结论与Miliordos 和Mavridis[17]的相同.

23Π 态具有明显的多参考特征,其在Re处主要价电子组态为1σ22σ13σ21π14σ05σ0(0.6130)和1σ22σ23σ01π14σ15σ0(0.2370).因此,从a3Π 态到23Π态的主要电子跃迁是2σ → 3σ 和3σ → 4σ.23Π 态与b3Σ—态在R=0.18920 nm 处交叉,交叉点位于23Π态的Re附近,23Π(υ′≥0)能级将受到b3Σ—(υ′≥6)能级的微扰,这解释了实验上未报道23Π 态光谱的原因.

弱束缚态15Σ—通过2σ → 1π 和3σ → 1π 的双电子激发形成,其在Re处的主要价电子组态为1σ22σ13σ11π24σ05σ0(0.9645).它的势阱深度为882.07 cm—1,仅包含3 个振动态.2σ → 1π 和3σ →4σ 的双电子激发形成排斥态15Π.

3.2 17 个Ω 态的光谱常数

SOC 效应使B 原子的基态2Pu和第一激发态4Pg分别分裂成2P1/2和2P3/2组分以及4P1/2,4P3/2和4P5/2组分.因此,前两个离解极限B(2Pu)+H(2Sg)和B(4Pg)+H(2Sg)分裂成5 条离解极限,即B(2P1/2) +H(2S1/2),B(2P3/2)+H(2S1/2),B(4P1/2)+H(2S1/2),B(4P3/2)+H(2S1/2)和B(4P5/2)+H(2S1/2).表3中列入了这5 个离解极限的能量间隔及它们所产生的23 个Ω 态.

由表3 可知,本文利用icMRCI+Q/56+CV+SR+SOC 计算的B 原子2P3/2—2P1/2,4P1/2—2P3/2,4P3/2—4P1/2和4P5/2—4P3/2的能量间隔分别与相应实验值[30]的差别仅为0.715 cm—1,263.915-xcm—1,0.600 cm—1和0.410 cm—1.17 个束缚和准束缚Ω 态的光谱常数见表4.

表3 BH 分子23 个Ω 态的离解关系Table 3.Dissociation relationships of the 23 Ω states of the BH molecule.

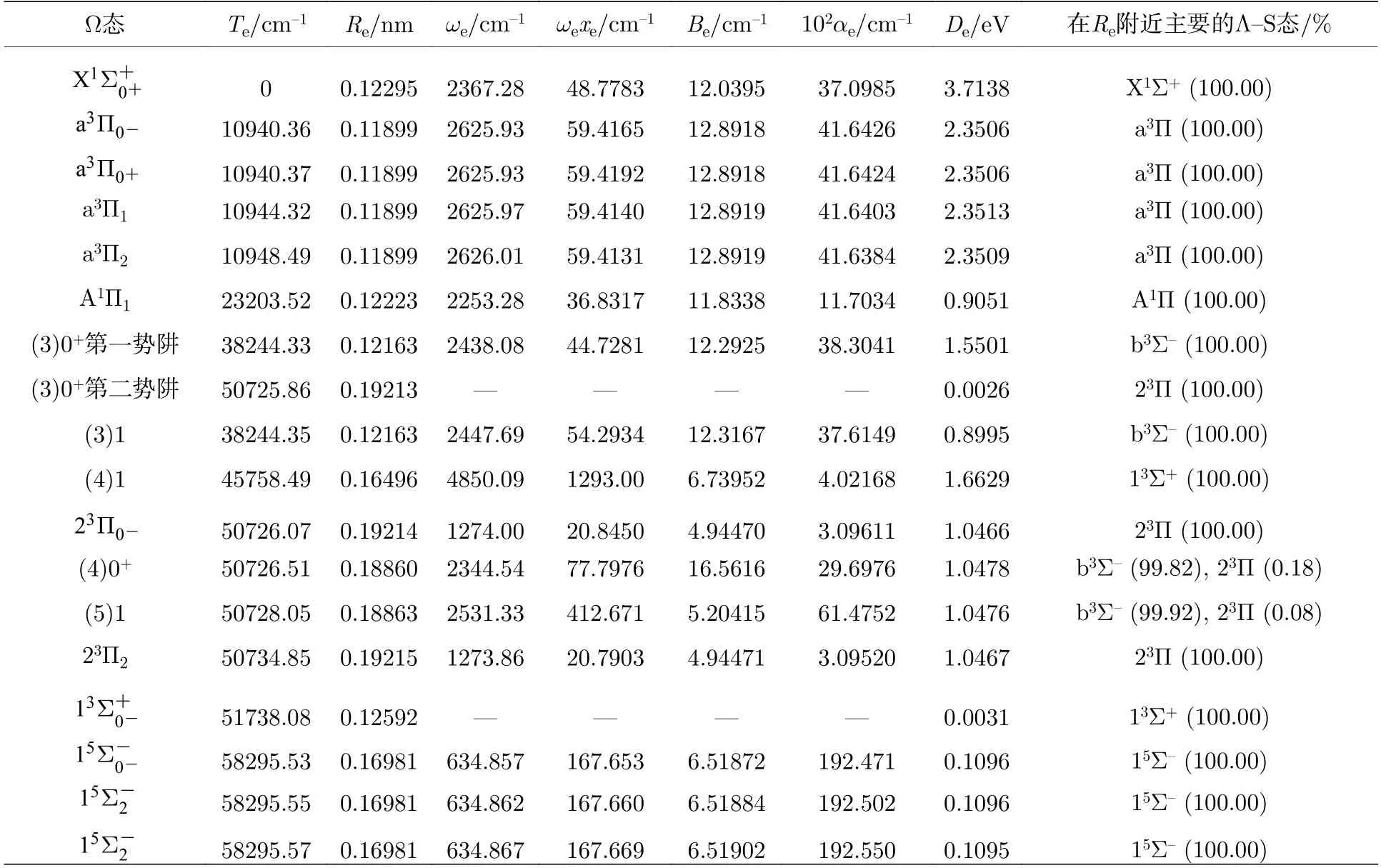
表4 利用icMRCI+Q/56+CV+SR+SOC 理论计算获得的17 个Ω 态的光谱常数Table 4.Spectroscopic parameters obtained by the icMRCI+Q/56+CV+SR+SOC calculations for the 17 Ω states.

在—25.084165 至—25.060894 Hartree 的能量范围内,b3Σ—态的势能曲线与13Σ+和23Π 态的势能曲线交叉;考虑SOC 效应后,这3 个Λ-S 态分裂出的Ω=0+和1 的成分出现避免交叉,这导致(3)0+,(4)0+,(3)1,(4)1 和(5)1 态势能曲线的形状和相应Λ-S 态势能曲线的形状不同,并且这5 个Ω 态出现了一些局域势阱;因此,这5 个Ω 态的光谱常数也有很大的变化.

13Σ+分裂出的态、23Π 态分裂出的23Π0−和23Π2与其它Ω 态没有避免交叉.由表2 和表4 可知,它们的光谱常数与相应Λ-S 态的光谱常数的差别也很小.

SOC 效应使排斥态 15Π 态分裂为 15Π−1,15Π0−,15Π0+,15Π1,15Π2和 15Π36 个Ω 态.

3.3 跃迁特性和激光冷却方案

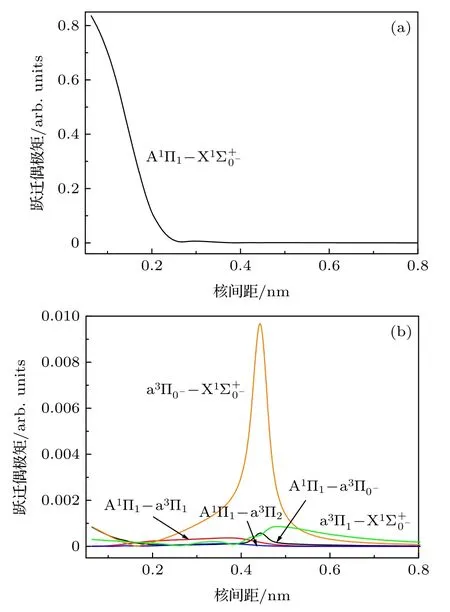
图3 BH 分子6 对跃迁的跃迁偶极矩曲线Fig.3.Curves of the transition dipole moments versus internuclear separation of six-pair states of the BH molecule.

表5 A1Π1(υ′,J′=1,+) → X 1 (υ′′,J′′=1,—)跃迁的跃迁波数(v˜)、爱因斯坦A 系数(Aυ′υ′′)、振动分支比(Rυ′υ′′)、Table 5.The transition wavenumber (v˜),Einstein A-coefficients (Aυ′υ′′),vibrational branching ratios (Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths (gfυ′υ′′) for the A1Π1(υ′,J′=1,+) → X 1 (υ′′,J′′=1,—) transitions.波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)

表5 A1Π1(υ′,J′=1,+) → X 1 (υ′′,J′′=1,—)跃迁的跃迁波数(v˜)、爱因斯坦A 系数(Aυ′υ′′)、振动分支比(Rυ′υ′′)、Table 5.The transition wavenumber (v˜),Einstein A-coefficients (Aυ′υ′′),vibrational branching ratios (Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths (gfυ′υ′′) for the A1Π1(υ′,J′=1,+) → X 1 (υ′′,J′′=1,—) transitions.波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)

表6 a 3Π0+ (υ′,J′=0,+) → X 1 (υ′′,J′′=1,—)跃迁的跃迁波数(v˜)、爱因斯坦A 系数(Aυ′υ′′)、振动分支比Table 6.The transition wavenumber(),Einstein A-coefficients(Aυ′υ′′),vibrational branching ratios (Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths (gfυ′υ′′) for the a 3Π0+ (υ′,J′=0,+) → X 1 (υ′′,J′′=1,—) transitions.(Rυ′υ′′)、波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)

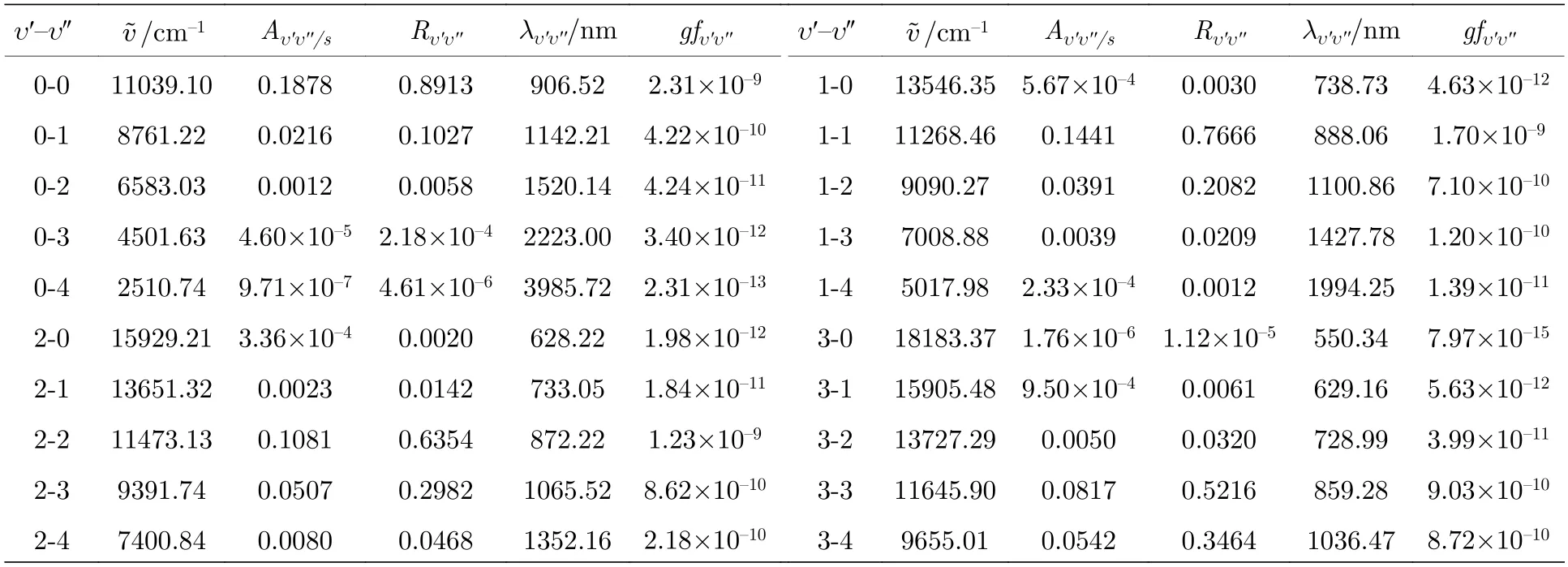
表6 a 3Π0+ (υ′,J′=0,+) → X 1 (υ′′,J′′=1,—)跃迁的跃迁波数(v˜)、爱因斯坦A 系数(Aυ′υ′′)、振动分支比Table 6.The transition wavenumber(),Einstein A-coefficients(Aυ′υ′′),vibrational branching ratios (Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths (gfυ′υ′′) for the a 3Π0+ (υ′,J′=0,+) → X 1 (υ′′,J′′=1,—) transitions.(Rυ′υ′′)、波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)

表7 a3Π1(υ′,J′=1,+) → X 1 (υ′′,J′′=1,—)跃迁的跃迁波数(v˜)、爱因斯坦A 系数(Aυ′υ′′)、振动分支比(Rυ′υ′′)、Table 7.The transition wavenumber (),Einstein A-coefficients(Aυ′υ′′),vibrational branching ratios (Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths (gfυ′υ′′) for the a3Π1(υ′,J′=1,+) → X 1 (υ′′,J′′=1,—).波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)

表7 a3Π1(υ′,J′=1,+) → X 1 (υ′′,J′′=1,—)跃迁的跃迁波数(v˜)、爱因斯坦A 系数(Aυ′υ′′)、振动分支比(Rυ′υ′′)、Table 7.The transition wavenumber (),Einstein A-coefficients(Aυ′υ′′),vibrational branching ratios (Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths (gfυ′υ′′) for the a3Π1(υ′,J′=1,+) → X 1 (υ′′,J′′=1,—).波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)

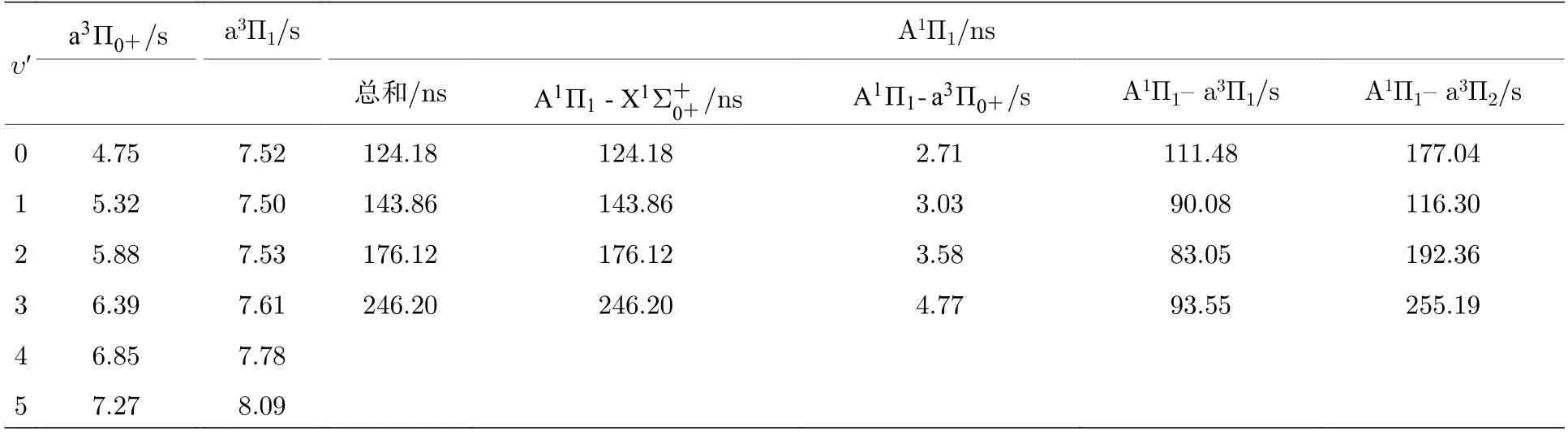
表8 A1Π1(υ′,J′=1,+),a 3Π0+ (υ′,J′=0,+)和a3Π1(υ′,J′=1,+)态的辐射寿命(τυ’)Table 8.Spontaneous radiative lifetimes(τυ′) for the A1Π1(υ′,J′=1,+),a 3Π0+ (υ′,J′=0,+)和a3Π1(υ′,J′=1,+) transitions.

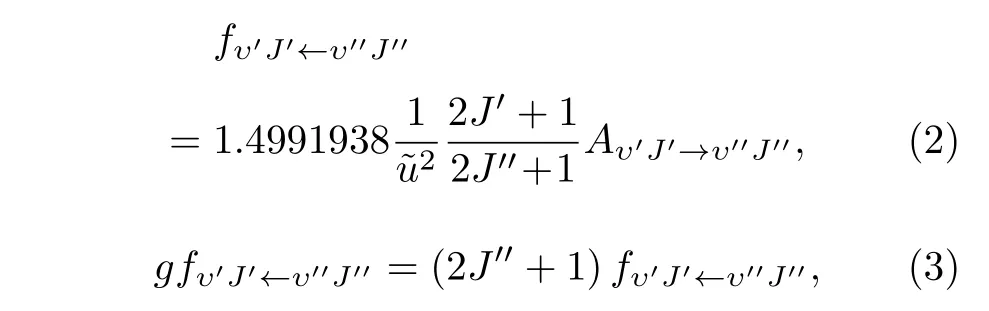
图4 利用A1Π1(υ′) ↔ (υ′′)跃迁进行激光冷却BH 分子的方案. 虚线表示A1Π1(υ′ = 0, 1) → (υ′′ =0 —3)跃迁的自发辐射振动分支比(Rυ′υ′′). 红色实线表示激光驱动 (υ′′) → A1Π1 (υ′)跃迁Fig. 4. The proposed laser cooling scheme for the BH using A1Π1(υ′) ↔ (υ′′) transition. The dotted line indicate the spontaneous radiation vibrational branching ratio (Rυ′υ′′) of A1Π1(υ′ = 0, 1) → (υ′′ = 0 — 3) transition. The red solid line indicate the wavelength (λυ′′υ′) at which the laser drives the (υ′′) →A1Π1 (υ′). transition.

4 结论

附录A

表A1 A1Π1(υ′,J′=1,+) → a 3Π0+ (υ′′,J′′=1,—)跃迁的跃迁波数()、爱因斯坦A 系数(Aυ′υ′′)、振动分支比(Rυ′υ′′)、波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)Table A1.The transition wavenumber (),Einstein A—coefficients (Aυ′υ′′),vibrational branching ratios(Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths (gfυ′υ′′) for the A1Π1(υ′,J′=1,+) → (υ′′,J′′=1,—) transitions.

表A1 A1Π1(υ′,J′=1,+) → a 3Π0+ (υ′′,J′′=1,—)跃迁的跃迁波数()、爱因斯坦A 系数(Aυ′υ′′)、振动分支比(Rυ′υ′′)、波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)Table A1.The transition wavenumber (),Einstein A—coefficients (Aυ′υ′′),vibrational branching ratios(Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths (gfυ′υ′′) for the A1Π1(υ′,J′=1,+) → (υ′′,J′′=1,—) transitions.

表A2 A1Π1(υ′,J′=1,+) → a3Π1(υ′′,J′′=1,—)跃迁的跃迁波数()、爱因斯坦A 系数(Aυ′υ′′)、振动分支比(Rυ′υ′′)、波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)Table A2.The transition wavenumber (),Einstein A—coefficients (Aυ′υ′′),vibrational branching ratios(Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths (gfυ′υ′′) for the A1Π1(υ′,J′=1,+) → a3Π1(υ′′,J′′=1,—) transitions.

表A2 A1Π1(υ′,J′=1,+) → a3Π1(υ′′,J′′=1,—)跃迁的跃迁波数()、爱因斯坦A 系数(Aυ′υ′′)、振动分支比(Rυ′υ′′)、波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)Table A2.The transition wavenumber (),Einstein A—coefficients (Aυ′υ′′),vibrational branching ratios(Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths (gfυ′υ′′) for the A1Π1(υ′,J′=1,+) → a3Π1(υ′′,J′′=1,—) transitions.

表A3 A1Π1(υ′,J′=1,+) → a3Π2(υ′′,J′′=2,—)跃迁的跃迁波数()、爱因斯坦A 系数(Aυ′υ′′)、振动分支比(Rυ′υ′′)、波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)Table A3.The transition wavenumber (),Einstein A—coefficients(Aυ′υ′′),vibrational branching ratios(Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths(gfυ′υ′′) for the A1Π1(υ′,J′=1,+) → a3Π2(υ′′,J′′=2,—) transitions.

表A3 A1Π1(υ′,J′=1,+) → a3Π2(υ′′,J′′=2,—)跃迁的跃迁波数()、爱因斯坦A 系数(Aυ′υ′′)、振动分支比(Rυ′υ′′)、波长(λυ′υ′′)、加权的吸收振子强度(gfυ′υ′′)Table A3.The transition wavenumber (),Einstein A—coefficients(Aυ′υ′′),vibrational branching ratios(Rυ′υ′′),wavelength(λυ′υ′′),and weighted absorption oscillator strengths(gfυ′υ′′) for the A1Π1(υ′,J′=1,+) → a3Π2(υ′′,J′′=2,—) transitions.