开放教育数学课堂教学质量模糊综合评价研究

潘灵荣

（浙江广播电视大学温岭学院，浙江温岭 317500）

1 课堂评价研究现状

课堂教学质量评价是当前的热门选题之一，学者们重点围绕评价指标的构建和评价方法的选择开展研究。朱瑛[1]对某校成人教育课堂教学质量评价进行了调查分析，指出评价主体单一、主观性强、方式不灵活、过程烦琐和评价结果利用不合理等问题，并给出相应的对策建议。李洪龙等[2]对高校课堂教学质量评价指标体系进行全新构建，运用结构方程模型和层次分析法确立评价指标及其权重赋值，并应用于实践。许宇翔等[3]运用PCA主成分分析法，对四川电大远程教育开放学生参加几何基础课程评价后数据进行降维处理，计算出反应四川电大教师教学质量的主要成分并建立教学质量评价模型。以上研究均采用精确数值进行调查分析和评价结果处理，忽视了决策者的主观模糊性，得到的结果可能与决策者的意愿有偏差。

三角模糊数于1965年被提出来，是为了解决不确定环境下的数值精度问题，应用于质量管理和风险管理领域为主[4]。肖逸璇等[5]利用三角模糊数改进层次分析法确定指标权重，并对评价结果进行分析，综合评价备选电压等级的优劣性问题。聂萍[6]通过理论研究与实证应用相结合、三角模糊数与模糊综合评价相结合的方法建立可持续发展视角下养老地产项目绩效评级体系和模型，识别出影响某养老地产项目绩效的因素并提出改进措施。

受以上学者启发，本文探索将三角模糊数、层次分析法和熵权法应用于开放教育数学课堂教学质量评价，通过评价指标构建、指标权重的确定和对评价结果的处理，综合评价开放教育数学课堂教学质量现状。最后，通过一个算例说明该评价方法的可行性和有效性。

2 开放教育数学课堂评价的指标体系

基于合理性、全面性、科学性和可持续性原则选取指标，借鉴“高校课堂教学评价”“数学课堂教学评价”和“数学课堂指标构建”等相关主题研究成果的基础上，结合开放教育数学课堂的内在特点，以5位长期从事开放教育数学教学的一线教师和教学管理人员作为专家评判小组，对初步取得的评价指标进行遴选和调整，最后经过三轮专家小组的讨论和意见收集，形成如表1所示的开放教育数学课堂质量评价指标体系。

表1 开放教育数学课堂质量评价指标体系

上述指标中，既有传统课堂教学的共性指标，也有开放教育数学课堂的特色指标，契合当下开放教育数学课堂的实际情况。

3 开放教育数学课堂的模糊综合评价

3.1 三角模糊数的定义

记三角模糊数M=（l，m，u），l和u分别为M的下限和上限，m是M的中值，也即最可能值，当l=m=u时，三角模糊数变为精确实数。令三角模糊数M的隶属函数为：

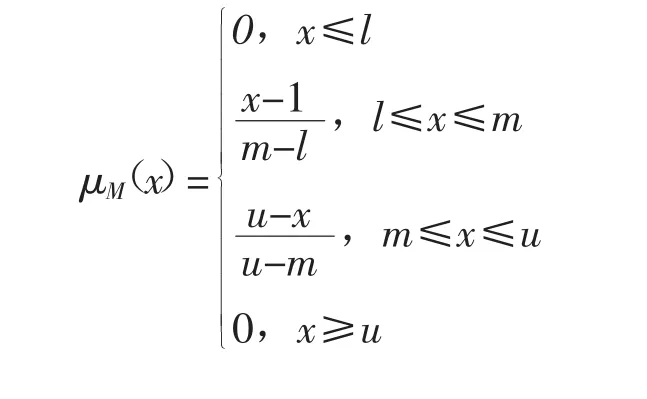
其运算法则定义如下：

若M1=（l1，m1，u1），M2=（l2，m2，u2），则有M1+M2=（l1+l2，m1+m2，u1+u2）；M1M2=（l1l2，m1m2，u1u2）；1/M1=（1/u1，1/m1，l/li）。

3.2 各指标权重的计算

按表2和表3的三角模糊数取值法进行赋分，构建判断矩阵。

表2 三角模糊数中值的取值1～9标度法

表3 三角模糊数上下界l和m的取值方法

3.2.1 主观权重（三角模糊数层次分析法）

3.2.2 客观权重（熵权法）

运用三角模糊数的运算定理，确定判断矩阵A的非模糊化矩阵。首先，对三角模糊数aij采用置信水平为α的水平截集置信空间进行替换，则A转化为

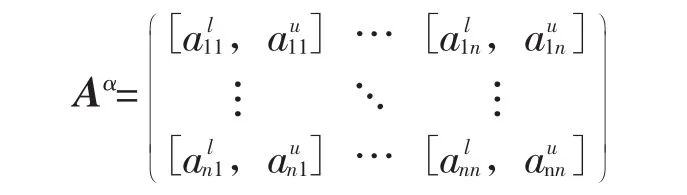
其次，保持α值不变，运用乐观指标系数β表示对指标相对重要度判断的满意程度。β的值越大，表示判断结果越有把握。可以表示为

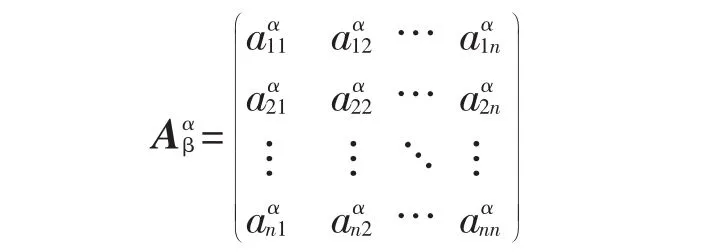
最后，根据熵和熵权的计算方法确定各指标的熵权fi[8]。

3.2.3 采用加权平均法

将两种评价方法的权重计算结果进行加权计算，并归一化处理

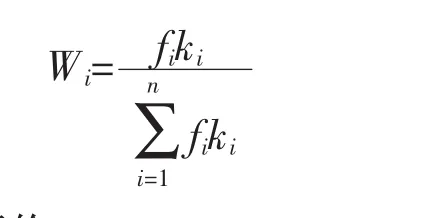
3.3 模糊综合评价

对于开放教育数学课堂质量评价属于二级模糊综合评价模型，具体的模型构建步骤如下：

3.3.1 确定因素层次

将被评价的因素集U分为n个因素子集U=（u1，u2，u3，…un），ui为第一层次即最高层次中的第i个因素，它由第二个层次中的m个因素决定，即 ui= （ui1，ui2，ui3…，uim）。

3.3.2 建立权重集

根据每一层次中各个因素的重要程度，分别赋予每个因素相应的权重值，记为

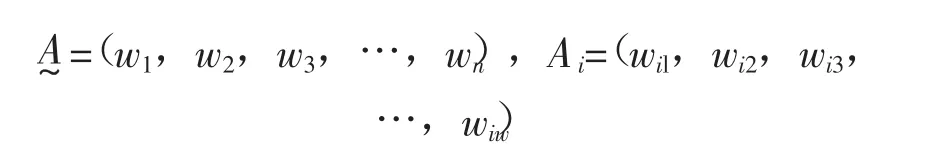
3.3.3 建立评语集

由于对评价系统状态及其因素状态的描述存在客观的模糊性，因而评语集一般可表示为V=（v1，v2，v3，…，vp）。

3.3.4 综合评价结果

因第一层次各因素都由第二层次的若干因素决定，所以第一层次每一因素的单因素评价应是第二层次的多因素综合评价结果。令第二层次的单因素评判矩阵为。

4 算例分析

以某基层开放大学数学课堂质量评价为例，运用上述评价步骤，进行如下计算。

4.1 指标权重计算

邀请5位数学高级讲师，对以上同层指标进行两两比较，得到各层的判断矩阵。

4.1.1 主观权重

以U为例，依据专家们的建议建立三角模糊数判断矩阵：

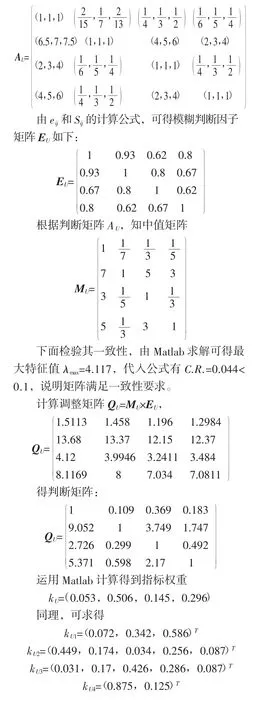
4.2 模糊评价结果

在因素集和权重集确定后，制作调查问卷并向理工专业学生下发，设置评语集为：差（P）=（0，0，25）；一般（F）=（0，25，50）；好（G）=（25，50，75）；很好（VG）=（50，75，100）；优秀（E）=（75，100，100），最终收集到有效问卷 50份。

通过对评价结果统计分析，得到开放教育数学课堂质量评价指标的评语集如下表4所示：

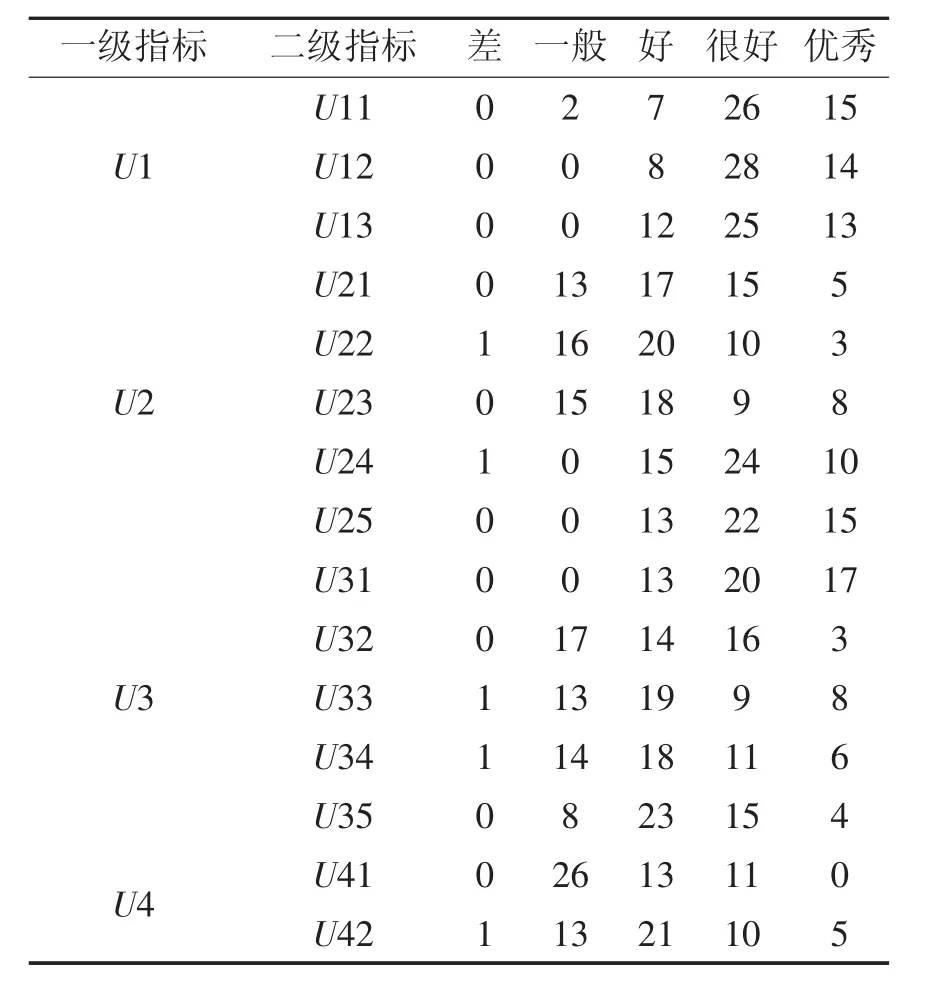
表4 开放教育数学课堂质量各指标权重及综合评价结果一览表

以U1为例，由二级指标评价集组成的模糊评价矩阵为：

结合指标权重结果，知U1对应指标的权重集为 WU1=（0.079，0.483，0.438），其评价结果为：

同理，可求得U2，U3和U4的评价结果分别是：

最后，计算目标层的模糊综合评价结果，由上可知：

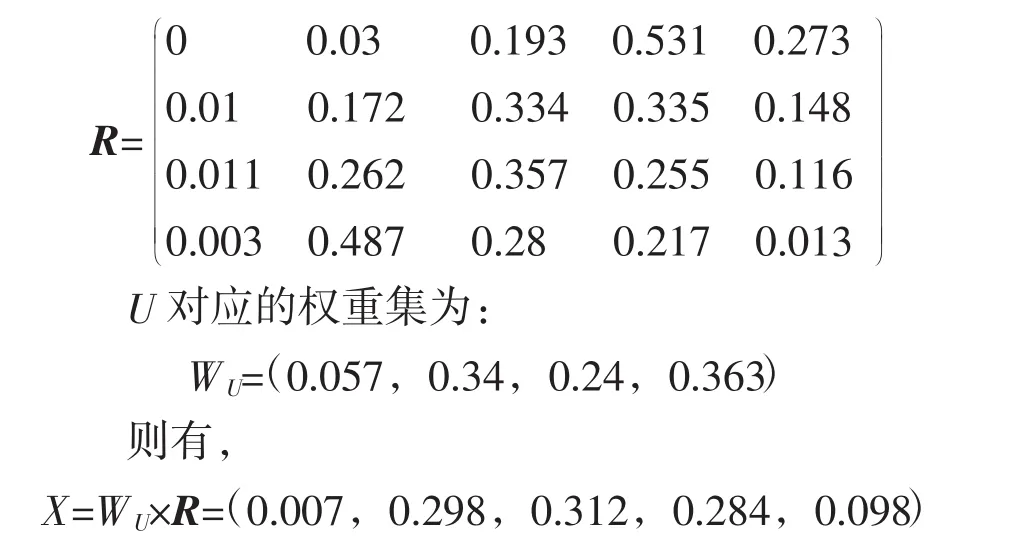
根据模糊数学中的最大隶属度原则，开放教育数学课堂质量评价结果的最大隶属度为0.312，对应的评语等级是“好”。

以上评价结果与实际的教学管理过程评价及学生的反馈结果基本一致。通过进一步分析可知：在方法上，以三角模糊数代替传统的精确实数，一定程度上防止了决策者有用信息的丢失，通过层次分析法和熵权法组合确权，避免了主观上的偏差；在指标权重上，U21、U22、U24、U34和U41占比较大，突出了开放教育数学课堂对数学重难点知识的内化、应用以及学科考核的重视；在评价结果上，该校数学课堂教学在教学态度和教学内容上获得了较高的学生评价，在教学方法和教学效果上略差些，说明学生对教学支持服务和课程内容体系是比较认同的，但在教学方式多样性和教学成果的输出上还不满意。整体而言，该评价方式计算较为简便，易于推广，不仅能为教师提供直观的评价结果，也为教师今后的教学改革指明了方向。

5 结束语

开放教育数学课堂质量评价是教学管理重要的一块内容，本文通过文献和实际结合构建了4个一级指标和15个二级指标的开放教育数学课堂质量评价体系，运用三角模糊数层次分析法和熵权法确定主客观权重，增加了权重获得的合理性，提高了评价结果的可信度。但随着教育信息技术与教学的深度融合，教学的物理场景在发生着变化，当前的指标体系仅适用于部分开放教育数学课堂质量评价情形，后续还应进一步深入研究。