基于修正的软化拉压杆模型的RC 框架边节点受剪性能研究
熊学玉,谢一凡,姚刚峰
(1. 同济大学建筑工程系,上海 200092;2. 同济大学先进土木工程材料教育部重点实验室,上海 200092;3. 苏州科技大学土木工程学院,苏州 215011)
框架节点作为传力中枢,是RC 框架结构的关键部位,对于保证框架的整体性起决定性作用[1]。在地震作用下,框架节点核心区受到弯矩、剪力、轴压力的共同作用,受力状态和传力机理十分复杂,属于应力紊乱区,不再满足平截面假定,其承载力由抗剪强度控制[2]。典型的RC 节点核心区受到的剪力可达框架柱内最大剪力的4 倍~6 倍[3]。因此,核心区受剪分析模型是框架节点研究热点[4-6]。
节点受剪研究主要关注以下两点:节点核心区受剪承载力和剪应力-剪应变骨架曲线。前者用于节点设计,实现强节点弱构件原则。后者可为数值模拟提供准确的理论模型基础。研究表明[7]:地震作用下,框架节点的受力后期会出现明显剪切变形,若忽略剪切变形,会导致模拟结果在刚度、承载力、滞回面积等方面误差较大。
目前存在的节点核心区受剪分析模型可分为三类:理论模型、经验模型和拉压杆模型[8]。理论模型[9-10]通过建立节点核心区剪切板的应变协调、平衡方程、本构关系,确定受剪承载力。理论模型可计算节点核心区的剪应力-剪应变骨架曲线和节点受剪承载力,但采用剪切板平均应力、应变假设,与框架节点实际受力不完全相符。研究表明[11]:理论模型与试验结果吻合相对较差,且对不同的试验结果的计算离散性较大。修正的斜压场理论[11](modified compression field theory, MCFT)在混凝土构件受剪计算中应用广泛。其理论公式为RC 配筋薄板剪切试验拟合得到。但板与RC 框架节点受力情况不完全相同,计算结果低估核心区配箍率较低的节点强度,高估配箍率较高的节点强度[12]。Mitra 等[12]基于MCFT 存在的上述问题,提出了约束斜压杆模型,假定节点核心区所有剪力均由混凝土斜压杆传递。箍筋和柱纵筋对节点受剪的贡献通过Mander 等[13]约束混凝土模型进行考虑。该模型计算思路简单,但使用Mander 等[13]本构导致模型对节点核心区骨架曲线下降段斜率的计算误差很大。模型只考虑箍筋对混凝土约束的贡献,没考虑箍筋本身承担的抗剪贡献。
其他两种模型只关注节点受剪承载力的计算。经验模型[14-16]通过试验数据对重要的影响参数进行回归,给出经验公式。缺点是缺乏比较明确的物理模型,且具有一定的适用范围。拉压杆模型[17-18]认为节点剪力通过对角混凝土压杆和钢筋拉杆传递。Hwang 等[19-20]考虑节点核心区混凝土在双轴拉压组合受力下的软化效应,建立了软化的拉压杆模型(Softened strut and tie model, SSTM)。并将其应用于RC 框架边、中节点,RC 深梁,牛腿,低矮剪力墙等应力紊乱区的计算[21],证明了SSTM 的广泛适用性。然而,SSTM 仍存在以下问题:
1) 混凝土斜压杆与水平线的夹角 θ采用简化假设,根据节点的几何尺寸确定,未考虑轴压比与节点长宽比的影响。与已有试验现象不符。
2) 拉压杆模型有意忽略的变形协调条件,只能给出承载力计算结果。考虑应变协调条件进行核心区骨架曲线计算的结果适用性尚待验证。
边节点与中节点相比,抗剪需求更高,抗剪强度较低[18]。准确计算边节点的受剪性能十分必要。
本文针对边节点受力特点,对斜压杆倾角公式进行修正,根据44 个边节点的剪应力-应变曲线数据拟合得到软化混凝土本构曲线,考虑混凝土开裂前刚度取值,提出MSSTM 模型 (Modified softened strut and tie model, MSSTM)。采用SSTM模型、MSSTM 模型和约束斜压杆模型对91 个RC边节点的受剪承载力和26 个边节点的骨架曲线进行计算,对比分析三模型的适用性。
1 MSSTM 模型建立
1.1 宏观模型
梁端弯矩和柱端弯矩、轴力同时作用于节点,梁柱纵筋受到的压力和拉力通过粘结作用传入节点核心区[22-23],形成沿对角线方向互相正交的斜向压力和拉力。SSTM 的框架节点抗剪机理如图1 所示。该抗剪机理由斜向机构、水平机构与竖向机构三部分共同组成,其中斜向机构如图1(a)所示。

图1 节点抗剪机构Fig. 1 Joint shear resisting mechanisms

研究表明[20]:轴压力增加,节点核心区裂缝形成的倾角变陡;节点受剪承载力[24]与节点长宽比成反相关。基于几何关系的假定未考虑两者的影响。斜压杆倾角的计算公式需修正。
根据边节点的受力特点可知,RC 节点斜压杆倾角可按图2 所示机制进行定义[25]。图2 中:hb为梁高;hc为柱高;ac、ab分别为柱端、梁端截面受压区的高度。图中阴影为混凝土受压的应变分布示意图。分别找到应变图的形心位置,作对应的柱、梁水平线的平行线形成交点,交点连线与水平线的夹角即可认为是斜压杆的倾角。由于三角形形心位置在1/3 处,因此,可得到计算公式如下:


图2 斜压杆倾角计算图Fig. 2 Calculation of angle of strut inclination
式(2)从应变分布层次给出了斜压杆倾角的计算公式。由式(3)可知,轴压力增大,柱端混凝土受压区高度增大,该公式计算的斜压杆的倾角变陡,与试验现象相符。
相应的斜压杆的面积Astr为:

图1(b)所示的水平机构由一个水平拉杆和两个平压杆(见阴影部分)组成。节点核心区箍筋构成了水平拉杆。图1(c)所示的竖向机构由一竖向拉杆和两个陡压杆组成,其中柱的非角部纵筋构成了竖向拉杆。
1.2 平衡方程
根据拉压杆模型,对节点列平衡方程,可得节点的水平剪力为:

当节点内存在三种机构参与抗剪时,水平拉杆和竖向拉杆各上述按比例占一部分,剩下的部分由斜向机构承担。结合式(10)~式(13),进行一定的代数变换,可得:

当节点核心区达到承载力时,认为核心区混凝土到达其抗压强度。根据结点区的受力平衡,可以得到 σd,max的计算公式:

1.3 本构关系
框架节点核心区混凝土由于双向受力,表现出软化效应。SSTM 采用Zhang 和Hsu[27]提出的开裂混凝土的软化本构曲线进行计算,如式(24)~式(26)所示。由于Hwang 计算节点的承载力,只取该本构的上升段[19]。


该本构根据配筋混凝土板的双向剪切试验进行回归得到,考虑了开裂混凝土双向受力引起的软化效应。但用于节点计算时存在以下问题:
1) 配筋混凝土板的边界条件与RC 框架节点有所不同,且板的厚度方向尺寸远小于平面内尺寸,可简化为平面应力问题。但框架节点厚度(宽度)方向与平面内尺寸相当,若简化为平面应力问题会有较大误差。
2) 该本构适用于混凝土板开裂后的应力-应变关系,当计算框架节点受剪承载力时,节点开裂严重,与该本构假定相符,因此适用性尚可;在计算RC 框架节点核心区在受力全过程的剪应力-剪应变骨架曲线时,由于加载前期核心区混凝土尚未开裂,混凝土尚未表现出软化效应,软化系数不适用。边节点核心区在平面内存在梁端与上下柱端的约束,与剪切板的边界条件差别较大。
上述分析可知,Zhang 和Hsu[27]提出的软化本构曲线对RC 节点核心区剪应力-剪应变骨架曲线的计算的适用性不足。本文对此进行修正:
笔者从已有文献中收集44 个RC 框架边节点的试验数据[24,28-32]。关键参数范围如表1 所示。混凝土强等级包括C25~C70;梁高在200 mm~750 mm;节点核心区配箍率在0%~1.72%;钢筋强度包含HRB300~HRB500;试验轴压比最大为0.25,对应设计轴压比约0.4。因此,可认为试验数据具有一定代表性。
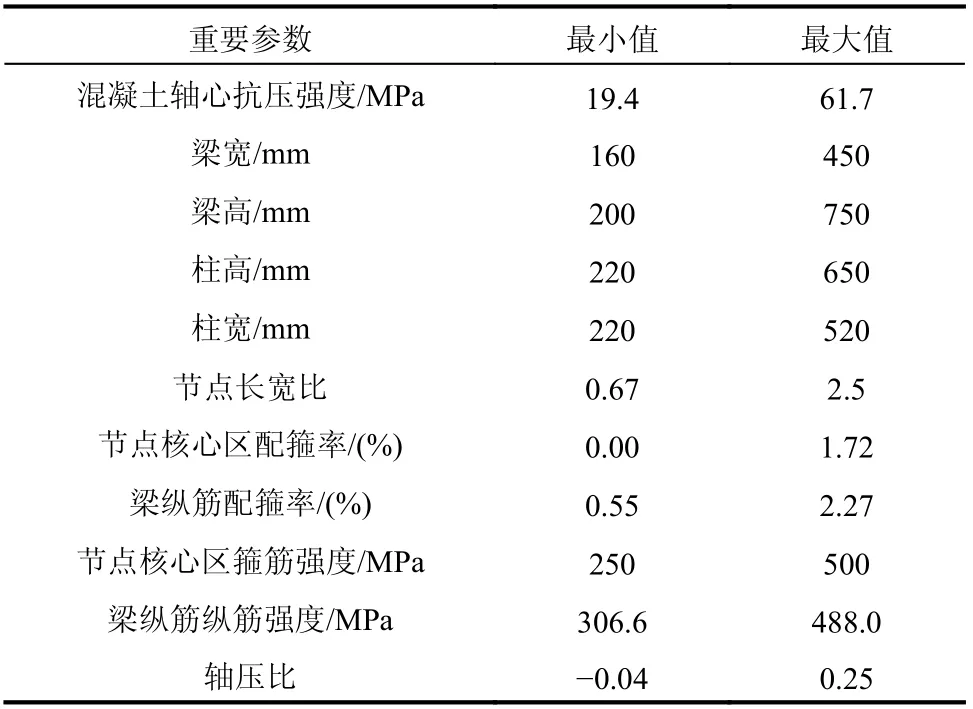
表1 试验数据范围Table 1 Range of test data
取上述节点核心区剪应力-剪应变骨架曲线试验数据点(每个试件上取关键点4 个~6 个),参考Zhang 和Hsu[27]的软化本构形式,对试验数据点进行拟合。得到新的混凝土软化本构曲线如式(28)~式(30)所示。

试验数据点与拟合得到的新本构曲线以及原本构曲线的对比如图3 所示。原公式下降段刚度过大,与试验数据相差较多;且对峰值的计算也偏大。拟合的新本构与试验数据较为吻合。


图3 基于边节点试验数据的软化混凝土本构拟合曲线Fig. 3 Proposed constitutive model of softened concrete for exterior joints
1.4 变形协调

1.5 求解过程


2 模型验证
2.1 试验数据库
为了验证上述框架节点受剪承载力计算模型的准确性,笔者对上述44 个边节点[24,28-32]和SSTM原文中给出的试件及其他数据完整试件[33-44]进行收集,共得到了91 个RC 边节点在反复荷载下的试验数据,以此对MSSTM 模型进行验证。试件选择的原则如下:
1) 边节点中存在楼板、横梁、梁柱有偏心的试件不予选取。
2) 边节点中梁纵筋在核心区锚固不足,发生纵筋锚固破坏的试件不予选取。
3) 边节点中最终发生柱端屈服破坏(CF)的试件不予选取。发生梁端屈服破坏(BF)、梁端屈服后节点核心区剪切破坏(BY-JS)、节点核心区剪切破坏(JS)的三种破坏模式的试件予以保留。
2.2 结果分析与讨论
1) 受剪承载力
为验证MSSTM 模型的正确性,对上述91 个边节点的受剪承载力进行了计算,同时采用SSTM模型和约束斜压杆模型进行对比。节点信息、三个模型的计算值与试验值的对比结果如表2 所示。
91 个试件中,35 个试件发生BF 破坏,由梁端受弯承载力控制,节点核心区尚未破坏;56 个试件发生BY-JS 破坏或JS 破坏,均为节点核心区破坏。合理的模型计算的BF 破坏节点承载力与试验值之比应略高于1。BY-JS 和JS 节点承载力与试验值之比应接近1,同时离散性较小。
由表2 可知,对BF 破坏的试件,采用SSTM模型、MSSTM 模型和约束斜压杆模型得到的试验值与计算值之比的平均值分别为1.147、1.104、1.375。对BY-JS、JS 破坏的试件平均值和变异系数 分 别 为1.028、0.995、1.203 和0.230、0.164、0.273。三模型对BF 破坏试件的计算平均值均大于1。考虑到按强节点弱构件原则设计时,节点承载力与剪力需求之比一般不会超过1.5,可认为约束斜压杆模型计算结果偏大。三模型对BY-JS、JS 破坏的试件计算MSSTM 模型最准确,且变异系数最小,说明离散性较小;SSTM 模型计算结果均值较好,但离散性大于MSSTM;约束斜压杆模型计算结果均值偏大,且离散性最大。

表2 框架边节点三模型计算值与试验值对比Table 2 Comparison of joint shear strength predictions with experimental results of three models

续表2

续表2

图4 边节点剪应力-剪应变骨架曲线计算流程图Fig. 4 Flow chart for shear strain-stress curve calculation
对BF 破坏试件,认为计算值与试验值之比大于1.5 或小于0.8 则为预测偏差;对BY-JS、JS 破坏试件,认为比值误差超过20%为预测偏差,则三模型表现如下表3。三模型中MSSTM 对不同破坏模式预测均最准确。

表3 三模型预测偏差Table 3 Unacceptable Prediction Ratio of Three Models
三模型受剪承载力的计算值和试验值的对比如图5 所示。由图5 可知,约束斜压杆模型由于只考虑斜压杆机构传递剪力,假设过于简单,因此适用性有一定局限,表现为对不同节点预测适用性较差。BF 破坏和BY-JS、JS 破坏的试件计算值与试验值之比最大值分别为3.22、1.83;最小值分别为0.57、0.61。对所有破坏模式的节点计算离散性最大。MSSTM 模型与约束斜压杆模型相比,包括了三种机构共同抗剪,考虑因素较为全面;与SSTM 模型相比,计算斜压杆与水平线夹角的计算中,考虑轴压比的影响,按混凝土应变分布得到公式,且软化混凝土本构选取得当,因此与试验值最为接近,离散性最小。

图5 三模型计算值与试验值对比Fig. 5 Comparison of joint shear strength prediction with experimental results of three models
将轴压比、节点长宽比和混凝土强度分别作为横轴变量,按不同破坏模式对比三模型的计算结果如图6、图7 所示。图6 中的节点核心区未破坏,计算值与试验值之比大于1 可认为合理。由图6(a)、图6(b)可知,SSTM 模型对轴压比在0.2以下、节点长宽比在1~1.5 的节点承载力计算结果准确性偏低。由图6(c)可知,SSTM 模型对混凝土强度在20 MPa~40 MPa 的节点承载力计算结果偏低。

图6 轴压比、节点长宽比、混凝土强度的影响(BF 破坏)Fig. 6 Effect of column axial ratio, joint aspect ratio and concrete compressive strength on joint shear strength (BF)
图7 为节点核心区破坏的节点,计算值与试验值之比等于1 可认为计算结果准确。由图7(a)可知,MSSTM 模型随轴压比的变化,其计算值与试验值之比仍在1 附近,而SSTM 模型逐渐偏离1,说明SSTM 模型未准确考虑轴压比的影响。由图7(b)可知,MSSTM 模型对不同节点长宽比的边节点适用性均较好。对节点长宽比大于1 的边节点,其计算结果显著较SSTM 模型更准确。由图7(c)可知,约束斜压杆模型对混凝土强度大于40 MPa 的试件,严重高估节点抗剪承载力。这可能是因为在约束斜压杆模型中,节点混凝土双向受力的软化系数根据普通混凝土试验数据回归得到。试验数据未包含高强混凝土节点,适用性存在局限。SSTM 模型对普通混凝土节点计算离散性较大,对高强混凝土节点计算效果较好;MSSTM模型对不同混凝土强度的节点整体计算离散性较为一致。

图7 轴压比、节点长宽比、混凝土强度的影响(BY-JS、JS 破坏)Fig. 7 Effect of column axial ratio, joint aspect ratio and concrete compressive strength on joint shear strength (BY-JS、JS)
斜向机构倾角对计算结果敏感。根据SSTM模型,三种抗剪机构按式(16)~式(18)所得比例分担水平剪力。不同斜压杆倾角时,三种机构承担剪力比例如图8 所示。 tanθ=1 ,即 θ=45°时,混凝土斜压杆传递水平剪力效率最高; tanθ >2,即θ> 63.5°时,竖向机构和斜向机构不传递水平剪力,全部剪力由水平箍筋承担。按SSTM 模型计算,试件H1.5S、M1.5S θ为62.5°,混凝土斜压杆几乎不传递剪力。节点承载力正比于水平箍筋用量。但试验结果表明:上述节点的核心区破坏严重,斜裂缝发展明显。混凝土不传递剪力这一假设显然与试验现象不符。经MSSTM 修正后,两试件 θ均为57°,混凝土斜压杆可传递部分剪力。计算值与试验值之比从0.75、0.7 变成1.07、1.01。说明修正方法具有合理性。

图8 不同机构剪力分配比例Fig. 8 Ratios of shear force distribution mechanisms
SSTM 模型与MSSTM 模型确定 θ与承载力预测准确度的关系如图9 所示。与SSTM 模型相比,MSSTM 模型计算 θ向45°靠拢,说明MSSTM的斜压杆分担剪力较大,是传递剪力的主要机构,更合理反应了节点破坏机理,整体计算结果更准确。

图9 斜向机构倾角的影响(BY-JS、JS 破坏)Fig. 9 Effect of angle of diagonal strut (BY-JS、JS)
轴压比增加,节点柱端受压区高度变大,增大了混凝土斜压杆的面积,进而增加节点受剪承载力;同时轴压比增加会改变节点核心区主应力方向,使核心区斜裂缝与水平夹角变陡。图10 为不同轴压比下,SSTM 模型与MSSTM 模型的 θ计算,试件#4、#5 轴压比为0.25,轴压比影响显著。按MSSTM 模型计算的 θ大于SSTM 模型,计算结果也有相应改善。说明MSSTM 模型可较好考虑轴压比影响。

图10 轴压比对斜向机构倾角的影响Fig. 10 Effect of axial force ratio on angle of diagonal strut
2) 剪应力-剪应变骨架曲线
MSSTM 模型根据收集到的边节点试验数据,得到拟合的软化混凝土本构;并在计算过程中,令开裂前的软化系数取1,改善了SSTM 模型开裂前刚度的计算准确性,部分程度提高了下降段刚度的计算效果;也较好地解决了约束斜压杆模型对开裂前刚度、下降段刚度计算与试验误差较大的问题。
三模型在峰值剪应力、峰值剪应变、开裂刚度的计算值与试验结果对比结果见表4。

表4 峰值应变、峰值应力、开裂刚度的试验值与三模型计算值的对比Table 4 Comparison of peak shear stain, stress and initial stiffness with experimental results of three models
SSTM 模型、约束斜压杆模型和MSSTM 模型对峰值应变计算值与试验值之比的平均值分别为1.54、5.43 和1.64;峰值应力之比的平均值分别为1.39、1.19 和1.14;开裂刚度之比的平均值分别为0.38、0.57 和1.02。说明MSSTM 模型能较为准确的计算边节点的峰值应变和峰值应力,在计算开裂前刚度准确程度较其余两模型有明显改善。
选择典型的试件进行三个模型骨架曲线与试验对比,如图11 所示。
以试件3 为例,说明典型边节点核心区骨架曲线的一般特征。加载初期,节点核心区混凝土未开裂,骨架曲线上变现为弹性,且斜率较大;当核心区混凝土主拉应变到达混凝土开裂应变时,混凝土核心区开裂,出现交叉斜裂缝,箍筋应变迅速增加,骨架曲线刚度减小,但承载力仍可上升;当节点核心区箍筋到达屈服,骨架曲线到达峰值,此时节点核心区交叉斜裂缝发展充分;随着进一步加载,节点核心区破坏严重,承载力迅速下降,骨架曲线进入下降段。
与SSTM 模型和约束斜压杆模型相比,MSSTM模型计算得到的峰值点、开裂前刚度明显与试验更符合,峰值后的下降段刚度有一定改善,但由于此时混凝土破坏严重,影响下降段刚度因素较多,结果具有一定离散性。其中图11(h)、图11(i)中的试件H0.7S 和H2.0S 的计算峰值应力准确性相对较差。原因如下:试件H0.7S 为梁端受弯破坏,节点基本完好,试验无法得到节点承载力,计算峰值应力高于试验值具有一定合理性。斜压杆面积计算中梁端受压区高度的计算公式(4)为近似公式。试件H0.7S 的节点长宽比为0.7,梁高相对较小。MSSTM 计算结果高度依赖斜压杆面积。对此类试件或可采用有限元或条带法准确计算梁端受压区高度,改善计算结果准确性,相关问题待进一步研究。文献[21]给出试件H2.0S 的破坏图,节点核心区破坏严重,且由于节点长宽比较大,梁、柱混凝土强度分别为26.4 MPa、48.2 MPa,节点核心区斜裂缝延伸至柱端,梁端裂缝开展不充分。初步分析认为试件H2.0S 属于节点核心区和柱端混合破坏(JS-CF)。破坏模式不属于BY-JS破坏,柱端破坏严重,受压区高度ac很小,式(3)已不适用该试件的计算。
图11(e)中的下降段刚度计算相对精确度较差。分析发现试验数据在强度下降后又有向上趋势,可能是节点变形过大时,加载装置提供额外刚度,对试验数据产生误差。


图11 三模型计算核心区剪应力-剪应变骨架曲线与试验对比Fig. 11 Comparison of shear strain stress curve with experimental results of three models
3 结论
本文针对框架边节点的理论计算进行了研究,得到如下结论:
(1) 针对SSTM 模型进行了修正,建立了MSSTM模型。对91 个框架边节点的受剪承载力的进行计算,并与SSTM 模型、约束斜压杆模型进行对比,结果表明:对56 个发生节点核心区破坏的节点,SSTM 模型、约束斜压杆模型和MSSTM 模型计算值与试验值之比的平均值分别为1.028、1.203和0.995,变异系数分别为0.230、0.273 和0.164,说明MSSTM 模型计算结果较为准确,且离散性最小。
(2) 对26 个边节点的核心区剪应力-剪应变骨架曲线进行了计算,与SSTM 模型和约束斜压杆模型进行对比。三模型的峰值应变、峰值应力、开裂刚度的计算值与试验值之比的平均值分别为SSTM 模型:1.54、1.39 和0.38;约束斜压杆模型:5.43、1.19 和0.57;MSSTM 模型:1.64、1.14 和1.02。说明MSSTM 模型对核心区剪应力-剪应变骨架曲线的计算与试验结果更吻合。
(3) MSSTM 模型实现了节点受剪承载力和核心区剪应力-剪应变骨架曲线计算的双重目标,精度较好。因此可为RC 框架边节点的设计和有限元模拟[48-51]提供理论基础。

