一种超声波声速测量实验仿真软件的设计及实现
檀世博,黄继承,童 阳,欧艺文
(湖北工业大学 理学院,湖北 武汉 430068)
超声波是一种频率大于20 kHz的纵波型声波,可在固、液、气三态中传播,具有波长短、方向性强、能量集中、反射能力强等优点。超声波传播速度的测量在超声波测距、液体液位测量、气体温度传感以及流量监测等方面发挥着愈来愈重要的作用,已成为主要检测技术之一。通常测量超声波声速的方法有两种,即驻波法和相位比较法[1-3]。这两种方法相比于干涉和衍射法,具有操作简单、易于实现的优点。驻波法和相位比较法的原理在于利用压电晶体的压电效应产生超声波,通过控制超声波在空气中的传播距离,分别观察驻波波形和李萨如图形,由其距离测得超声波的声速。因此,传统的超声波声速测量的实验需要购置函数信号发生器、示波器以及声速测量仪等硬件设备,使用成本高,参数的设置范围受限于仪器本身,需要占用专门场地或实验室。此外,传统实验法还存在易受环境噪声和压电晶体焦耳热的干扰、实验数据需手动记录处理和测量速度慢等不足。
Matalb图形用户界面(GUI)是一种由窗口、按键、菜单、光标和文字说明等组成的可视化计算机操作用户界面,集数值分析和图形显示功能于一体。用户编写程序时只需编写回调函数,操作时不需要浏览烦冗的代码,因此,Matlab GUI比C语言更简单实用。采用Matlab GUI编写实验所需的模拟软件,使用成本低,依靠计算机等智能设备便可以实现。实验仿真软件不仅直观形象,可以帮助实验者更好地理解实验原理与实验内容,而且可以使实验者不受实际条件限制,灵活修改实验参数,随时随地做实验,处理数据快捷精准,大大提高实验效率。MATLAB GUI还有一大优点就是能编译生成独立的.exe应用文件,用户不需要安装内存庞大的MATLAB软件就可以运行程序。Matlab GUI已经广泛应用于数字滤波器设计、图像处理、光学系统设计和物理实验演示等方面[4-6]。
本文提出采用Matlab GUI实现超声波声速的仿真测量,为超声波的声速测量领域提供了一种使用成本低、简便可行的方法。
1 实验原理
由于超声波的波长短,易于定向发射,所以用驻波法和相位比较法测量超声波在空气中的传播速度比较方便。超声波的产生与发射均由压电晶体S1(超声波发射器)的逆压效应(电致伸缩)来产生,而接收则由压电晶体S2(超声波接收器)的压电效应来实现,如图1所示。由波动理论可知,声波的传播速度v与声波频率f和波长之间的关系为
v=fλ
(1)
因此只要测出声波的频率和波长,就可以求出声速。其中声波频率可由产生声波的信号发射器的频率读出,波长则可用驻波法和相位比较法进行测量[7]。
1.1 驻波法
驻波法又称共振干涉法,其原理图如图1所示。
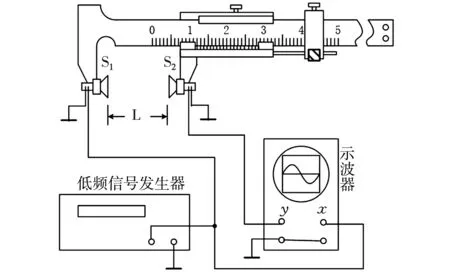
图1 超声波声速测量实验原理图
将低频信号发生器输出的正弦交变电信号加到压电晶体S1上,S1将按正弦规律发生纵向伸缩,产生超声波,并向周围空气定向发射近似平面波。压电晶体S2作为超声波接收器,在接收声波信号的同时反射部分超声波信号。如果接收面(S2)与发射面(S1)严格平行,入射波即在接收面上垂直反射。若不考虑超声波在空气中传播的能量损失,则入射波与反射波分别可以表示为:
(2)
(3)
式(2)和(3)中,y1、y2为质点振动位移,T为振动周期,A为振幅,λ为声波波长。入射波和反射波相互干涉,当发射面和发射面之间的距离正好等于半波长的整数倍时,形成驻波,其表达式为:
(4)
由于压电效应,接收器S2产生一个电信号。将此电信号输入示波器y轴,可以观察到驻波的波形。对于驻波而言,振幅极小的地方称为波节,振幅极大的地方称为波腹。相邻两个极大值之间的距离始终为λ/2。S2的反射面处是位移的波节、声压的波腹。改变发射面和发射面之间的距离,在一系列特定的距离上,空气中出现稳定的驻波现象。此时距离等于半波长的整数倍,即
(5)
驻波的幅度达到极大。同时在接收面上的声压波腹也相应地达到极大值,通过压电转换,产生的电信号的电压值也最大(示波器显示波形的幅值最大)。因此,若保持频率不变,通过测量相邻两次接收信号达到极大值时接收面之间的距离,即可得到该波的波长,再用式(1)计算出声速[7]。
1.2 相位比较法
波的传播是振动状态的传播,亦即相位的传播。在波的传播方向上,相位随着传播距离L不断变化,但任意两点间的相位差Δφ仅与距离有关,满足Δφ=2πL/λ。当传播距离是波长的整数倍时,相位差恰好是2π的整数倍。也就是说,相位每变化2π一个周期,传播距离正好变化一个波长λ。利用这个原理,可以精确地测量波长。相位比较法是通过观察发射波和接收波的相位差测出传播距离变化而获得超声波声速的一种方法。超声波发射器S1的发射波(入射波)输入示波器的x轴,超声波接收器S2的接收波(反射波)输入示波器的y轴。入射波和反射波的频率相同、振动方向相互垂直,它们分别在示波器x轴和y轴偏转极板处引起的振动为
x=A1cos(ωt+φ1)
(6)
y=A2cos(ωt+φ2)
(7)
联立式(6)和(7),消去时间t,便可得合振动的轨迹方程
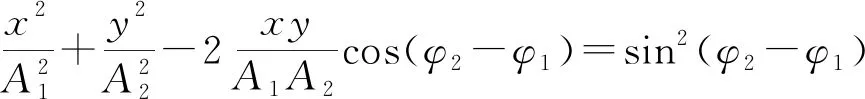
(8)
此即示波器上观察到的李萨如图形的表达式,可见一般情况下李萨如图形是一个稳定的椭圆。式(8)中φ2-φ1为入射波和反射波引起振动之间的位相差Δφ,由S1和S2之间的距离决定,即Δφ=2πL/λ。当两者的相位差Δφ=2nπ (n=1,2,3,…),即两个分振动同相,由式(8)可得
(9)
这表明李萨如图形为一斜率为正的直线,其斜率为两个分振动振幅之比。当两者的相位差Δφ=(2n+1)π(n=1,2,3,…)时,即两个分振动反相,由式(8)可得
(10)
这表明李萨如图形为一斜率为负的直线。显然,当连续出现斜率为正与斜率为负的直线时,对应的发射器与接收器之间距离的变化为半个波长,由此可以求得超声波波长,从而可以求出声速v=fλ,其中f为信号发射器的频率。
2 基于Matlab GUI的软件制作
2.1 登录界面的设计
超声波声速测量实验仿真软件的登录界面主要由两个可编辑文本框“用户名”“密码”和“登录”及“退出”两个按钮组成,如图2所示。“用户名”和“密码”的默认设置分别为shiyan和123456。实验者将它们输入对应文本框,点击“登录”即可进入实验主界面,点击“退出”则退出主界面。另外,注意在“密码”输入框后面设有“显示密码”按钮,方便实验者在无法正常登录的情况下检查输入的密码是否正确。

图2 实验仿真软件的登录界面
2.2 主界面的设计
超声波声速测量实验仿真软件的实验主界面包含三个菜单选项,即欢迎界面、实验内容界面和实验小结界面。
2.2.1 欢迎界面制作
“欢迎界面”由五个静态文本框构成,用于展示实验名称、制作团队成员和指导老师。
2.2.2 实验内容界面的设计
实验内容界面分为实验原理、视频讲解、驻波法测量实验和相位比较法测试实验四个模块,如图3所示。界面简洁,清晰明了,实验者按顺序操作后可了解实验的全部过程。
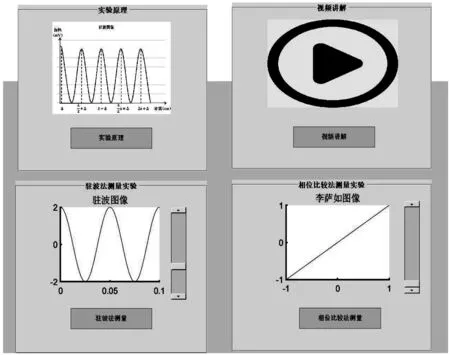
图3 实验内容界面
2.2.3 实验小结界面的设计
实验小结界面用于实验者记录实验所得的结论,包括驻波法测量实验结果的总结和相位比较法测量的结论。另外,该界面也可以让实验者进行扩展性实验,研究系统测量误差与信号发射器频率和环境温度的关系。
2.3 实验原理界面的设计
实验原理界面用于介绍驻波法和相位比较法测量超声波声速的原理,采用菜单编辑器制作成两个菜单而成。分别点击菜单选项,便可以查阅声速测量的原理,其主要内容与文中第1部分的相似。
2.4 驻波法测量实验界面的设计
驻波法测量实验界面如图4所示,分为图形显示、参数设置、数据记录、数据处理和误差分析五个模块[1,2]。
界面左侧为图形显示模块,包含上下两个图形窗口和帮助“Help”按钮。上面窗口用于显示入射波与反射波的波形,下面窗口则用于显示驻波图像。实验界面的设计思路和步骤是:
(1)建立2个坐标轴(Axes),分别用于显示入射波、反射波波形和驻波图像。
(2)添加1个按钮(Push button)HELP,点击“Help”按钮可弹出一个文本框,内有实验步骤和注意事项的简单说明,帮助实验者正确操作和完成实验。
(3)建立4个面板(Panel),分别用作参数设置、数据处理、数据记录和误差分析模块。
(4)参数设置模块中建立8个静态文本(Static Text),分别是信号发射频率、发射器与接收器之间距离L、起止范围、温度、温度单位℃;建立两个滑条(Slider),用于改变信号发射频率和距离L;建立1个可编辑编辑文本(Edit Text),用于输入温度。
(5)数据记录模块中建立一个列表框(listbox),用于存储出现驻波时L的值;2个按钮(Push button)分别是记录和清零表格数据功能;
(6)数据处理模块中建立1个按钮(Push button)用于运算;建立6个静态文本(Static Text),分别是逐差法求波长λ、波长单位mm、波速v、速度单位m/s、“=”;建立2个坐标轴(Axes)显示计算公式;建立2个可编辑文本(Edit Text)显示波长和波速。
(7)误差分析模块中建立1个按钮(Push button),用于计算波速理论值和误差百分比;建立6个静态文本(Static Text),分别是波速理论值、速度单位m/s、误差百分比、“%”“=”;2个可编辑文本(Edit Text),显示理论波速和误差百分比;建立2个坐标轴(Axes)显示计算公式。
2.5 相位比较法测量实验界面的设计
相位比较法测量实验界面和驻波法的类似,也含有图像显示、参数设置和数据记录五个部分,如图5所示。
上面两个图形窗口显示入射波与反射波,下面的图形窗口显示李萨如图形,同样可以设置发射频率,更改发射接收距离,可以计算出波长和波速,还可以计算出理论波速和误差百分比。
3 实验仿真的结果与分析
3.1 驻波法测波速的实验结果与分析
当信号发射器的频率为34.6 kHZ、室温为25 ℃时,调整超声波发射器和接收器之间的距离L,可以观察到入射波、反射波和驻波的图像显示窗口的一系列变化。当L恰好为超声波半波长的整数倍时,反射波与入射波的波形完全重合,两者相位相同,叠加发生相干干涉,形成如图6所示的驻波。可见驻波的极大值(波腹)是反射波与入射波幅值的两倍。连续拖动滑条,记录出现12个连续驻波极大值所对应的发射器和接收器之间距离。
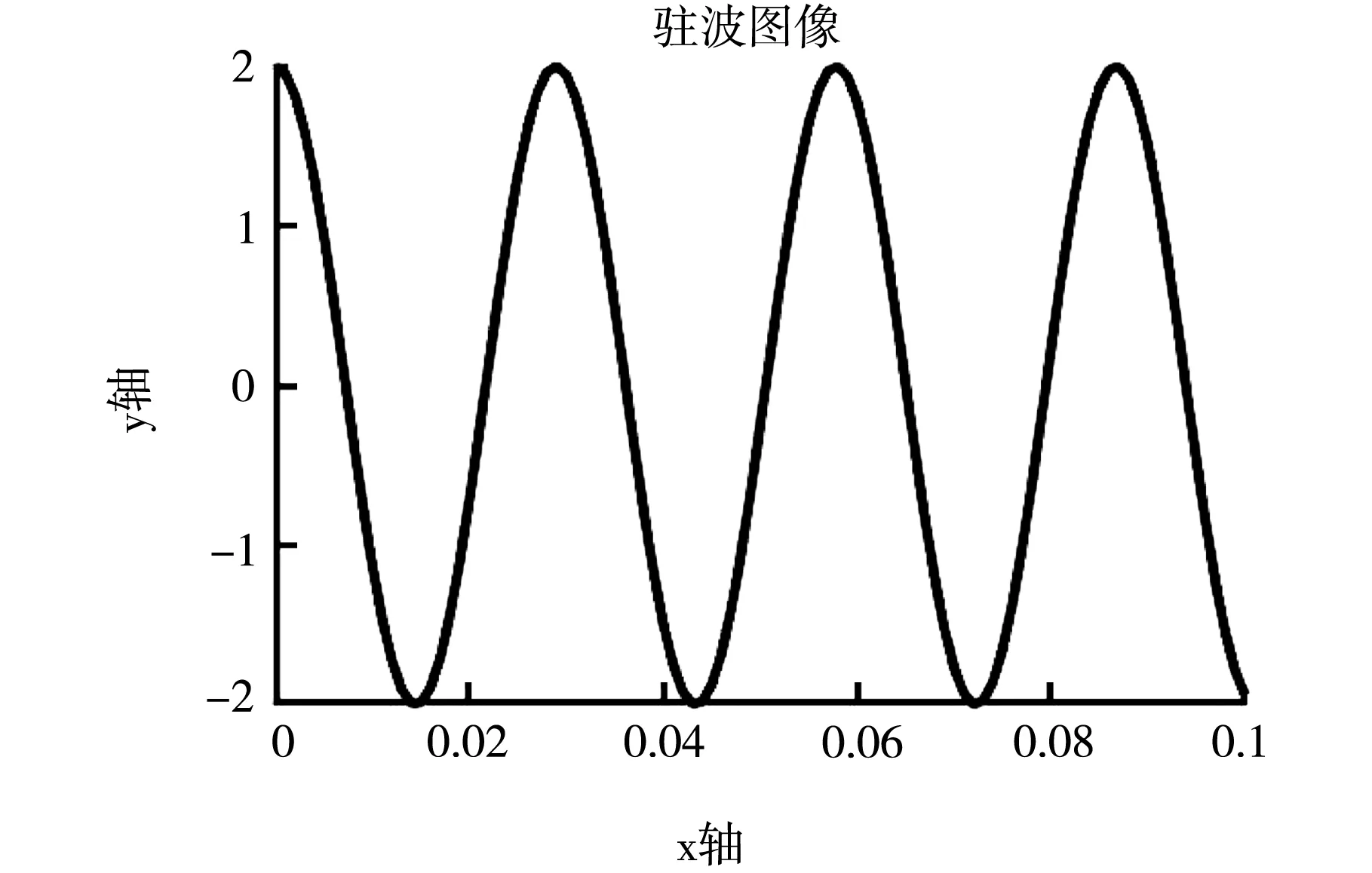
图6 形成的驻波波形
根据所得的数据计算出该条件下超声波波长为10 mm,波速为波速346 m/s。由公式ν=fλ可知,当室温为25 ℃时,理论波速为理论波速346.285 9 m/s,由此得到的实验误差为0.082 56%。这说明驻波法测得的超声波声速的误差很小,符合理论预期,实验软件可靠性强。
3.2 相位比较法测波速的实验结果与分析
设置实验信号发射器频率为34.6 KHz、室温为25 ℃。拖动滑条改变超声波发射器和接收器之间的距离L。当调节L使得反射波与入射波对应振动的相位相同时(见图7),说明两振动的相位差为2π的整数倍,合成后所得的李萨如图形为一斜率为正的直线,如图8所示。记录此时的发射接收距离。继续拖动滑条,连续11次出现斜率为正与斜率为负的直线时,记录对应的发射器与接收器之间的距离。根据所得的数据计算出该条件下超声波的波长为10 mm,波速为346 m/s。由公式可知,当室温为25 ℃时,理论波速为346.285 9 m/s,由此得到的实验误差为0.082 566%。可见采用相位比较法测得的超声波声速与理论值吻合良好,测量精度高。
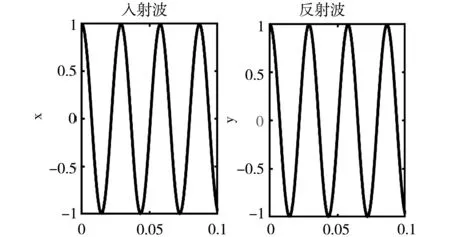
图7 入射波和反射波引起的振动
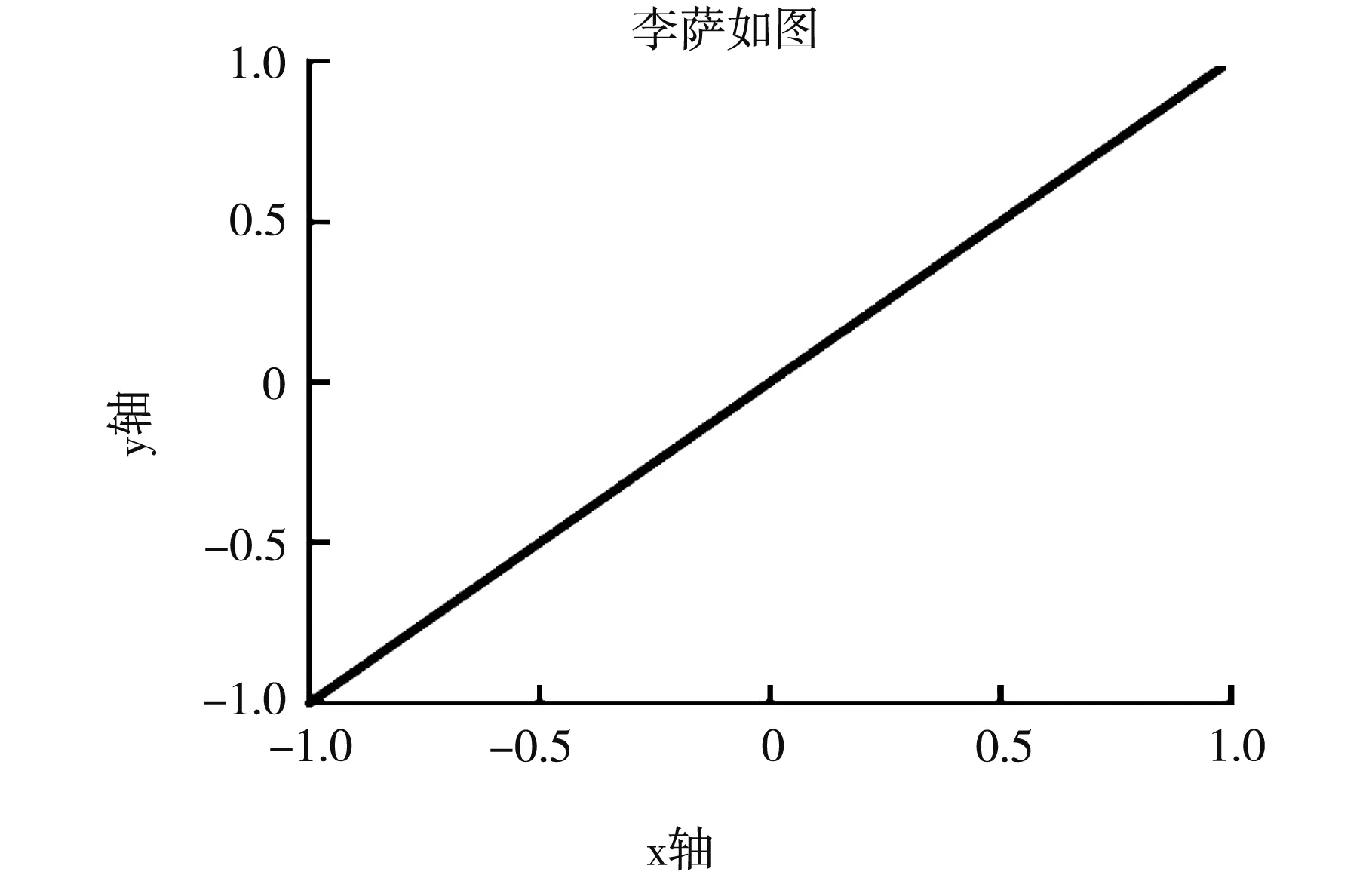
图8 形成的李萨如图像
3.3 扩展性实验结果与分析
在实验小结界面,当设置环境温度不变(如保持为20 ℃)时,采用驻波法可获得超声波声速误差与信号发射频率之间的关系曲线。可知误差随着频率的增大呈现出先减小后增大的变化趋势;当频率为21.5 kHz时,误差为0。而当使信号发射器的频率一定时,采用驻波法又可获得超声波声速的误差与温度的关系曲线。实验结果发现,当频率设定为32~33.7 kHz范围内的某个频率时,误差随着温度的增大而增大;当频率设定在33.8~35.4 kHz内时,误差随着温度的增加先减小后增大;当频率在35.5~37.0 kHz区间内时,误差随着温度的增加而减小。
4 结 语
本文采用Matlab GUI制作了一种用于超声波声速测量的实验仿真软件。该软件由登录、欢迎、实验内容和实验小结四个界面组成。仿真软件分别运用驻波法和相位比较法测量了超声波在空气中的传播速度,对比理论计算值,获得的相对误差小于0.1%。此外,采用该软件还研究了误差与信号发射频率和环境温度之间的关系,获得了一些可扩展性的结论。实验结果表明,该仿真软件不但功能齐全、使用成本低、占用内存小、参数设置灵活可控和数据处理快捷精准,而且测量结果符合理论预期、可靠性强、直观形象、界面友好、操作简单,提高了实验者的实验兴趣,加深了其对实验原理的理解。因此该仿真软件为超声波声速测量提供了一种行之有效的技术与手段。

