应用于经颅磁刺激的双8 字线圈设计与优化*
陈海雷,冉雪红
(重庆邮电大学光电工程学院,重庆 400065)
自20 世纪80 年代诞生以来,经颅磁刺激技术(Transcranial Magentic Stimulation,TMS),因其无创、无痛等优点在神经康复治疗方面具有广泛应用[1-3]。磁刺激线圈是将时变电流转化为特定磁场、感应电场的重要载体,是整个磁刺激技术的核心,也是系统设计的重点和难点,它决定着磁刺激的强度、深度和聚焦性[4-6]。
1985 年Baker 及其同事研制出圆形线圈用于刺激人体运动皮层[7]。圆形线圈结构简单,便于参数化设计,由于圆形线圈的聚焦性较差,多用于外周神经刺激。1988 年Ueno 等[8]设计了8 字形线圈,在实验室条件下实现了局部大脑皮层磁刺激,提高了线圈电场的聚焦性。近年来研究者通过对各种线圈进行了大量建模分析,结果表明8 字形刺激线圈是感应电场聚焦性能较好的一种方案[9-13],而8 字形线圈也是目前使用较广泛的刺激线圈单元。研究者围绕8 字线圈形状进行设计,如锥形线圈[14]、D 型线圈。
本文在圆形8 字线圈的基础上,针对半径和匝数等参数进行仿真,设计优化了双8 字线圈,结构下层为大半径线圈,上层为小半径线圈,以提高目标平面内的电场聚焦性及刺激强度,并寻求可实现较佳刺激的结构。同时采用较为真实的头部模型与传统型8 字线圈、双8 字线圈联合仿真,分析了头部不同区域的场分布,并对聚焦性及刺激深度进行了比较分析,更符合应用场景,具有较好的工程价值。
1 理论分析
Maxwell 方程解释了时变电磁场的运动规律,在无源空间中,有安培定律:
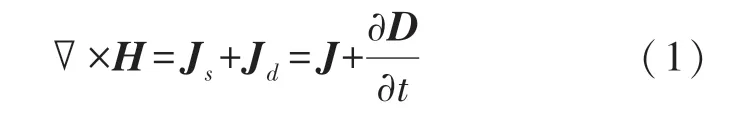
式中:H是产生的磁场强度,磁感应强度B通过磁导率μ与H联系起来,B=μH,磁导率与导体的材料和频率有关。Js是源电流密度,Jd是位移电流密度,D是电位移,与电场E的本构关系为D=εE,ε为介电常数,也与材料属性和频率有关。为了更好地分析电流与磁场的关系,以一个单线圈进行分析。
单线圈结构示意图如图1 所示,根据毕奥-萨伐尔定律可知,任意电流回路上任一闭合回路在场点P(x,y,z)所产生的磁感应强度B可表示为:
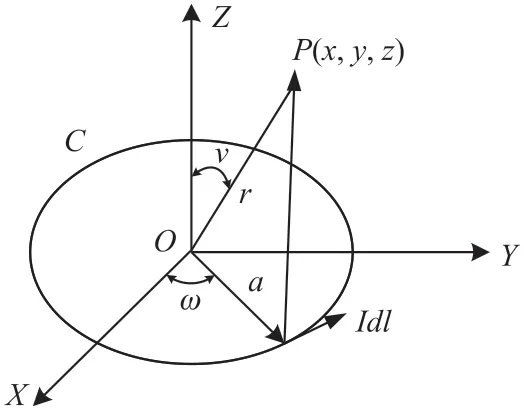
图1 单刺激线圈结构示意图
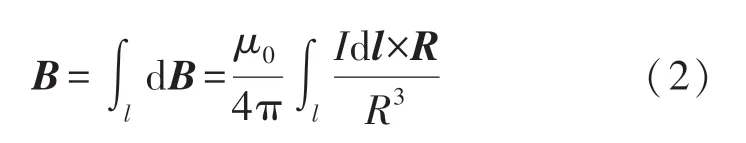
式中:μ0=4π×10-7H/m 为真空磁导率,R为电流元到空间任一点P的位置矢量。为计算简便引入磁矢量A,满足:
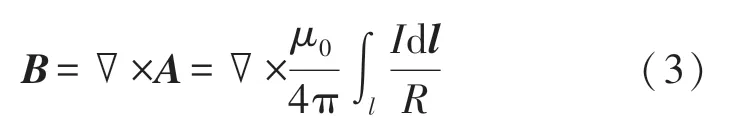
若施加电流为i(t)=Icos(ωt),则磁场和感应电场可分别表示为[15]:
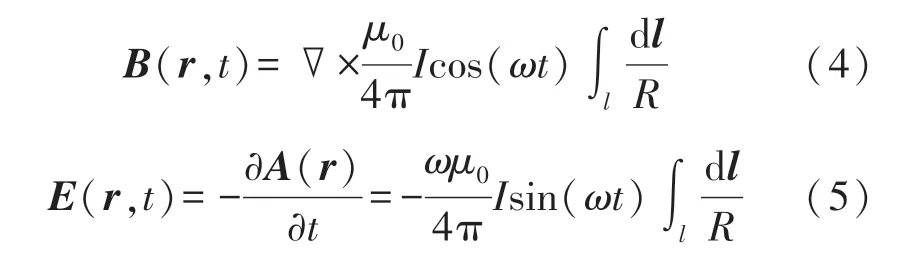
由式(4)、式(5)可以看出,时变的电流可以在空间中激发出电场和磁场,该法则也适用于人体组织[16]。
在线圈产生的电磁场性能评价指标中,通常采用半功率值区域(half power region,HPR)量化聚焦程度,HPR 指场值大于极值倍的区域等,本文采用HPR 为电场值等于或大于极值Emax的所组成的区域[17]:

如图2 所示,HPR 值越小,则表示场聚集性越好。为便于各线圈性能比较,本文提取HPR 面积占比,即半功率值HPR 在目标平面内所占比例。用此方式对路径上场点进行相似处理,定义半宽度区(half width region,HWR),如图3 即表示最大场强Emax衰减到其时场点组成的宽度。同时定义坡度:
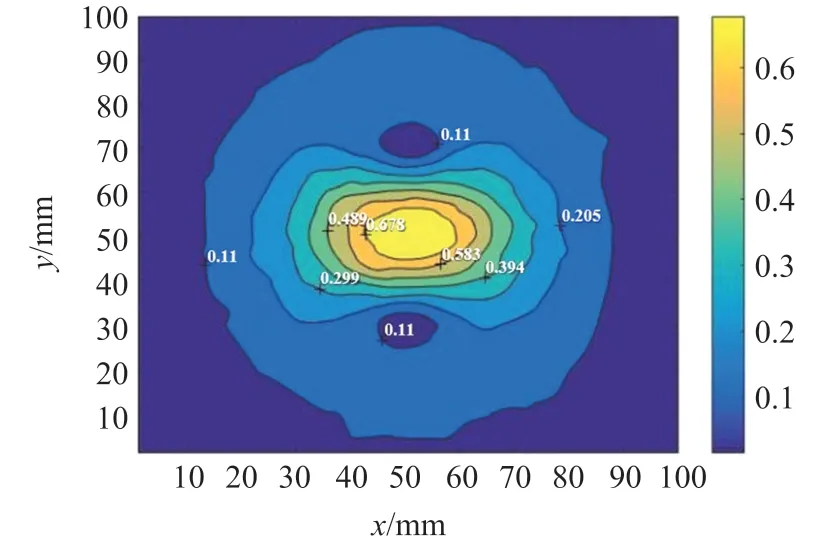
图2 半功率值区域(HPR)示意图
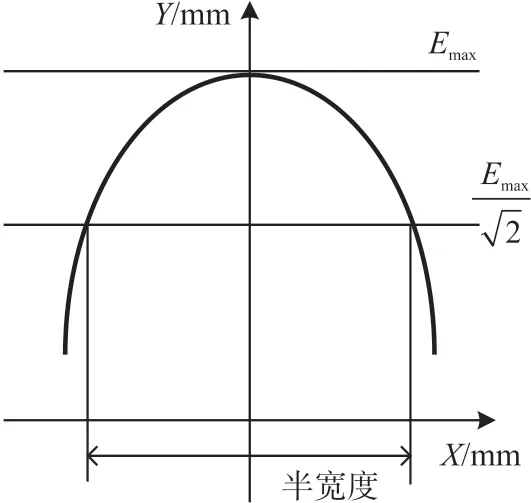
图3 半宽度区域(HWR)示意图
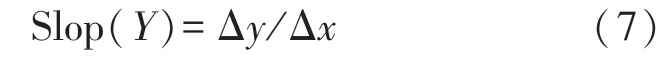
式中:Δy表示场极值与其倍的差值,Δx表示场极值对应位置与极值倍处对应位置的差值。半宽度越小表示在此路径聚焦性越好,坡度越大表示场值衰减速度越快。
2 结构设计与仿真
2.1 半径比仿真
8 字线圈是由两个相同的单个线圈组成,相切并平行放置。设计的双8 字线圈材料为铜,下层线圈仍为传统型8 字线圈,内半径为28 mm,线宽1.5 mm,匝数为10 匝。上层线圈在下层线圈上方0.1 mm 处,内径以2 mm 为步进,在10 mm~28 mm 变化。所有线圈匝数相同且均为1 000,频率f=10 kHz,每层电流相反,两层线圈的同侧电流方向相同。上层线圈内径为14 mm 时的线圈模型及电流方向如图4 所示。
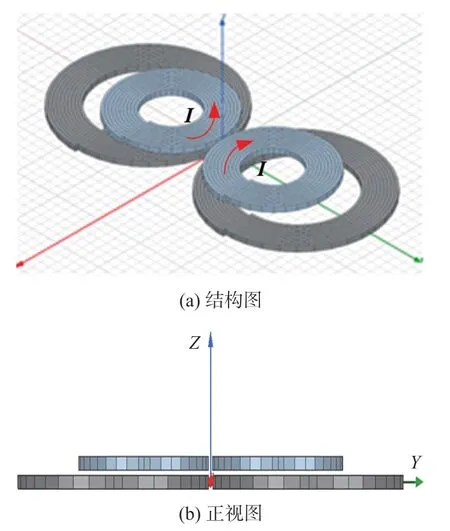
图4 双8 字线圈示意图
图5 为目标平面内切向与径向半宽度及半功率值,可以看出,随着上层线圈半径的增加,整体的半宽度呈增加趋势。目标平面内的半功率值在上层内径为10 mm 时较小,随后半功率值增加,并在内半径为20 mm 时出现较小值,在22 mm~28 mm 时半功率值较大。各个线圈在目标平面内的场极值与半功率值和单层传统线圈的数据对比如表1 所示。
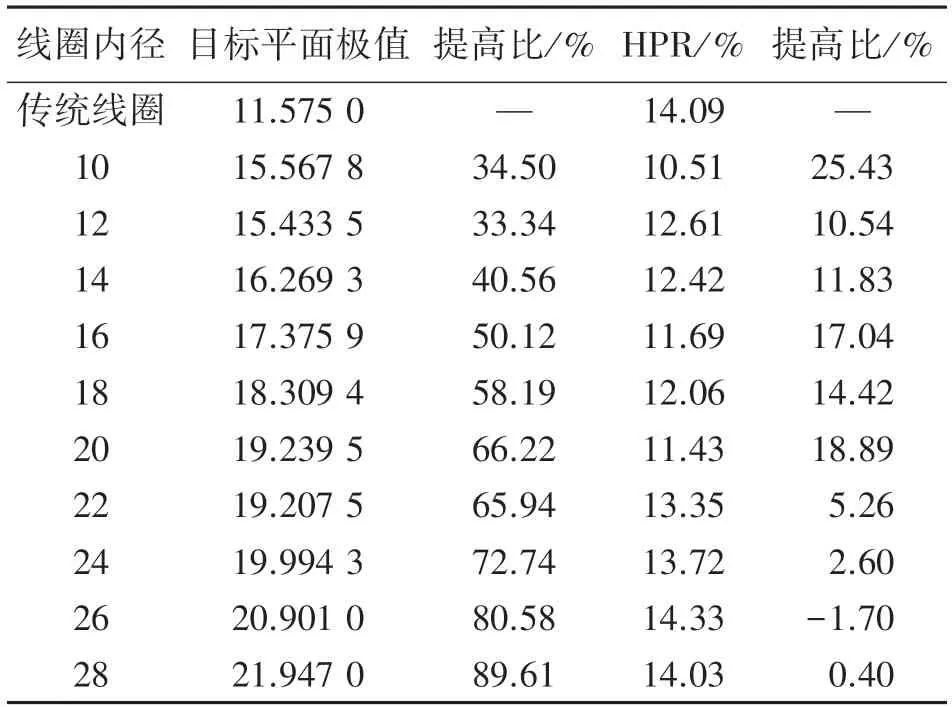
表1 双层线圈较传统线圈场极值及半功率值对比
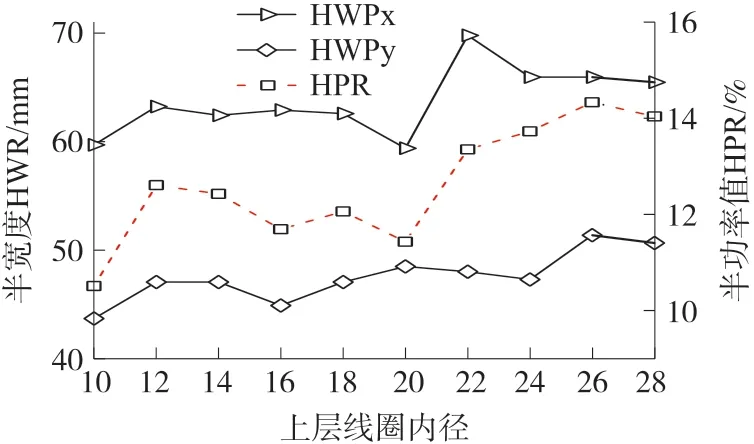
图5 目标平面内半宽度及半功率值分布
由表1 可以看出,目标平面内的感应电场极值较传统线圈均有较大增加,上层半径越大,场值提高比例越高;而半功率值在上层线圈内径为10 mm 时提高比约为25.43%,在半径为20 mm 时提高比约为18.89%,但在半径为28 mm 时目标平面内场极值较大。图6 为线圈在法向线Z 的数值分布,由图6 可以看出,随着上层线圈半径的增加,法向衰减坡度增加,衰减速度加快。综上,当上层线圈半径为20 mm时,即上、下层线圈内半径比为5/7 时,线圈刺激聚焦性及刺激强度获得较优解。
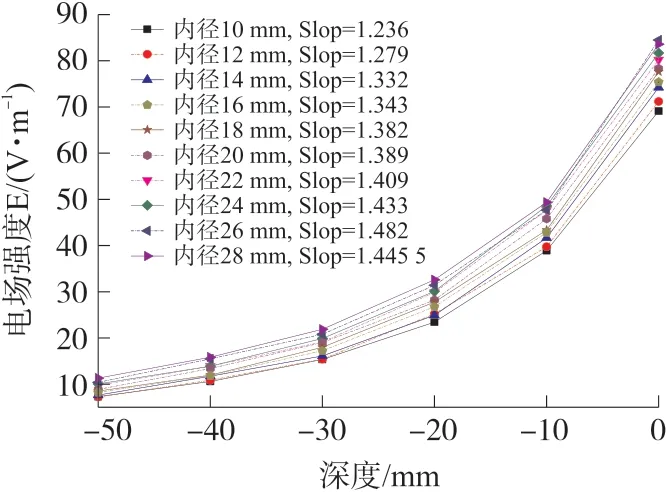
图6 线圈在法向线Z 的数值分布
2.2 匝数比优化
根据2.1 节分析结果,对双8 字线圈的上层线圈的匝数进行设计,研究上、下层线圈匝数比对目标平面内场分布的影响。上层线圈内径为20 mm,匝数在5~15内变化,每匝电流激励为100 A,频率f=10 kHz。上层线圈匝数为5 和10 时的线圈模型分别如图7 所示。

图7 上层线圈不同匝数模型
在目标平面内的场分布结果如图8 所示。切向线上的半宽度,随着线圈半径的增加先逐渐减小,达到9 匝时较小,随后逐渐增大;径向线的半宽度也在上层线圈为9 匝时较小。目标平面内的半功率值在上层线圈为9 匝时较小,且比线圈为10 匝时提高11.3%,但场极值较之低3.9%。与传统线圈相比,上层线圈为9 匝时,半功率值提高20.9%,目标平面内场极值提高57.8%,说明双层线圈较单层线圈在刺激强度和刺激聚焦性上有较大的优势。图8(b)为线圈在法向Z场衰减分布情况,随着匝数增加,电场值越大,法向衰减加快。综上,当上层匝数为9 匝时,即上、下层线圈匝数比为0.9 时,双八字线圈在聚焦性及刺激强度方面较传统型线圈较佳,此双8 字线圈在目标平面的感应电场分布如图9 所示。
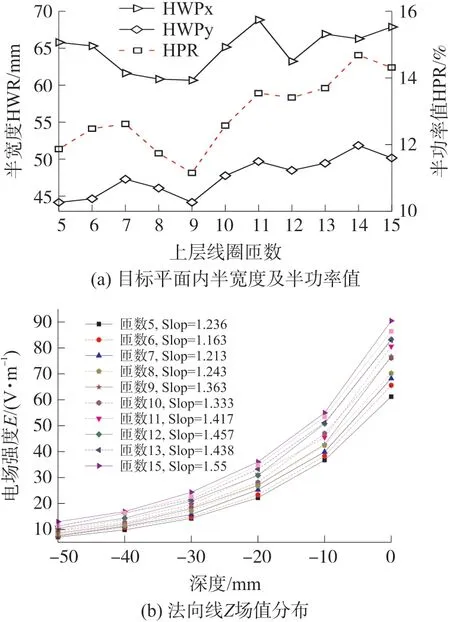
图8 不同匝数线圈感应电场值分布
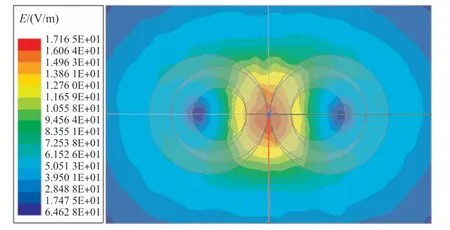
图9 双8 字线圈在目标平面内感应电场分布
2.3 头部联合仿真
联合仿真使用美国纽约城市大学Huang Yu 团队提出的ICBM-NY(New York Head)[20]头部模型,双8字结构为2.2 节优化后的线圈,为上下两层结构,上层线圈内半径为20 mm,匝数为9 匝;下层线圈内半径为28 mm,匝数为10 匝,下层线圈仿真在头顶上方5 mm 处。每个线圈的单匝电流激励均为100 A,频率为10 kHz,线圈位置及电流方向如图10 所示,线圈在头部的感应电场分布如图11 所示。

图10 线圈位置及电流方向图
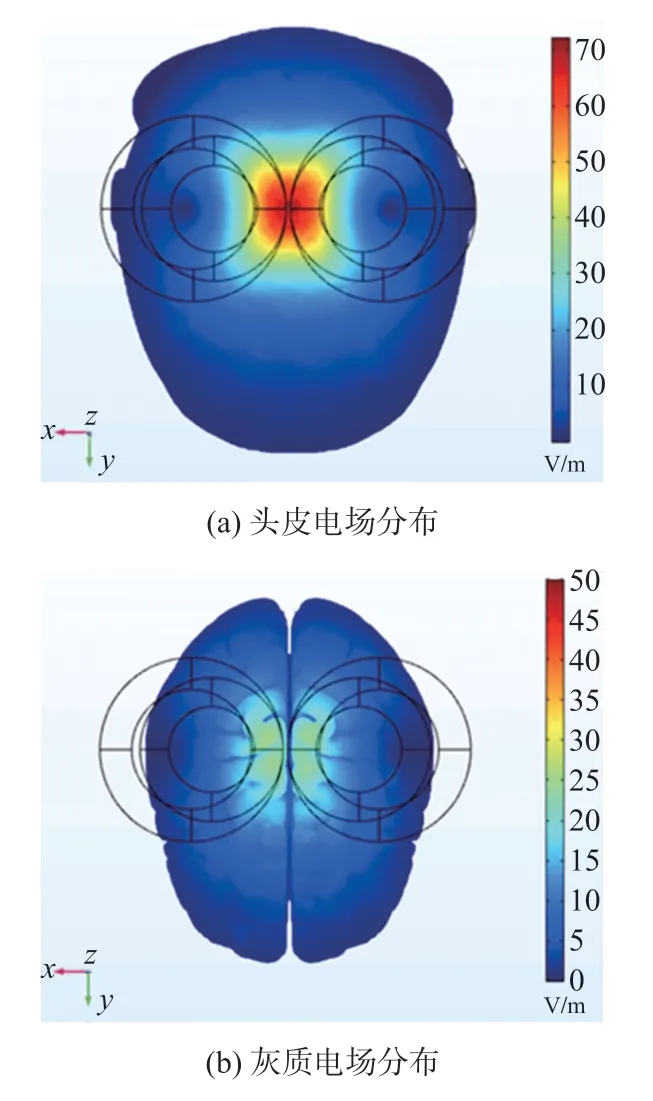
图11 双8 字线圈在头部的感应电场分布
为更好地体现两种线圈在头部的刺激效果,在线圈下30 mm 平面内作两条测试线,即径向线Y及切向线X以体现场的分布情况,并沿线圈相切处作法向线Z,以研究电场在头部的衰减性,各线段在头部的位置如图12 所示。
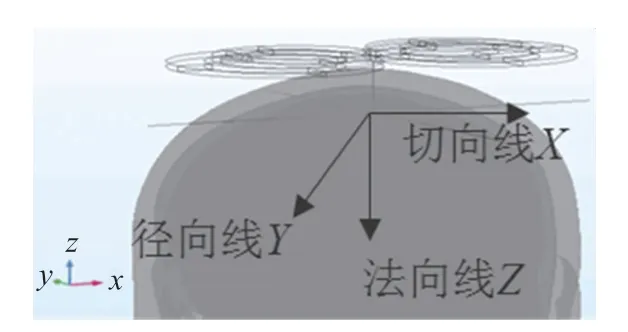
图12 三条测试线在头部的位置
图13 为两种刺激线圈在测试线X、Y、Z上的感应电场幅值分布图。图13(a)是两种线圈在径向线X和切向线Y中的场分布,其中传统型线圈在径向线X、切向线Y的半宽度分别为92.75 mm、45.4 mm,双8 字线圈相应的半宽度分别为61.46 mm、45.84 mm,可以看出两种线圈在切向线的分布情况类似,双8 字的场在径向方向分布更有优势。图13(b)是沿法向线Z在头部的感应电场分布,双8 字线圈的衰减坡度为1.2,传统型8 字线圈的衰减坡度为0.48,双8 字线圈的感应电场衰减较快,与线圈分析的结果趋势较为一致。

图13 头部中各测试线上的场分布
为较全面体现线圈刺激性能,引入目标函数S以表征电场在头部的聚焦性,假设刺激时头皮的感应电场的极值为Emax,目标函数表示为:

传统型8 字线圈及双8 字线圈的刺激参数如表2 所示,由表中数据可看出,双8 字线圈的目标函数较传统型8 字线圈的低约56.4%,因此双8 字线圈在聚焦性及刺激深度方面更为优异。

表2 传统8 字线圈及双8 字线圈的参数比较
表2 中,Emax为刺激时头皮的感应电场的极值;为头部电场值小于所构成的体积,表示为刺激体积;为法向线Z上等于点距头顶的距离,表示为刺激深度;表示目标函数,表征电场在头部的聚焦性,数值越小,表明刺激聚焦性越佳。
3 测试与讨论
为更好地分析线圈的磁场分布,我们使用CH-1600 数字高斯计对切向线X、径向线Y及法向线Z等磁感应强度幅值进行测量。数字高斯计CH-1600如图14(a)所示,其主要利用霍尔效应法,通过霍尔探头对空间磁场进行采集及分析,选用三维轴向高斯计探头,直流测量分辨率可达1×10-5mT,交流测量分辨率为0.01 mT,测量频率范围是2 Hz~2.5 kHz,并且可以通过采集卡及数据读取软件对脉冲磁场等进行测量及显示,软件显示磁场的波形界面如图14(b)所示。

图14 CH-1600 数字高斯计及测试效果图
由于直流电源功率受限,脉冲电路产生的磁场极为微弱,高斯计精度无法精确探测及显示,因此在对直流刺激线圈激发出的磁场的分布情况进行测试时,将直流电压源输出电压设置为3 V,设备显示输出电流为2.44 A,传统8 字线圈和双8 字线圈的磁场测试效果图分别如图14(c)、14(d)所示。
高斯计测得径向线Y、切向线X及法向线Z上的磁感应强度数值分布及仿真分布结果如图15 所示。由图15(a)可看出,线圈上方30 mm 的径向线Y上的磁场在两线圈的相切处数值较小,在各自线圈的中心处数值较大,远离线圈的位置数值迅速减小,且双8 字线圈的场强较大;图15(b)所示的是线圈上方30 mm 处切向线X的场分布,在线圈相切位置的场强较大,远离中心后场值逐渐减小,此时双8字线圈场强分布切合度较好;图15(c)是在线圈相切处的法向Z的场值分布图,远离线圈后亦呈逐渐衰减趋势,且双8 字线圈场强相对较高。由于磁场强度较小,测量时易受外界干扰,各测试线的实测结果与仿真结果在一定的误差范围内趋势较为一致。
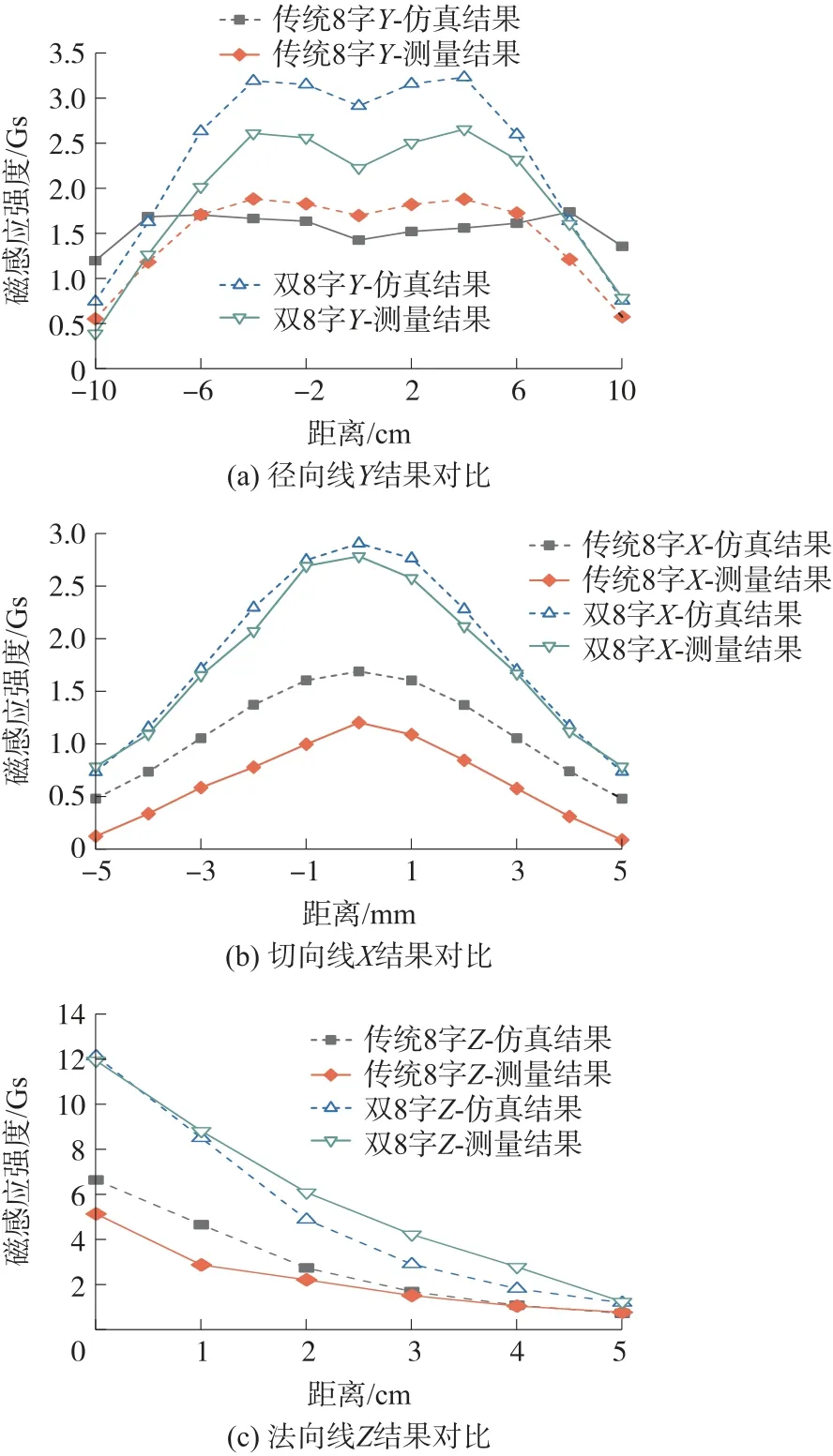
图15 各测试线磁场仿真与测试结果对比
4 结论
本文基于磁刺激线圈基本理论和场叠加原理,在传统8 字线圈的基础上设计并优化了双8 字磁刺激线圈。分别从线圈内径和匝数比进行了优化,实现了可产生较佳刺激的结构。仿真与测试结果表明,该结构提高了目标平面内的电场聚焦性及刺激强度,具有较好的工程应用价值。后续可以设计更加完善的保护及检测电路,提高刺激功率,同时制作效率更高的多通道参数可控电路,从而进一步推进TMS 在临床的应用。

