大规模空气质量监测数据缺失处理方法实证研究

张 波,宋国君

大规模空气质量监测数据缺失处理方法实证研究

张 波,宋国君*

(中国人民大学环境学院,北京 100872)

基于2016年1月至2021年7月的全国1654个国控监测点小时级的6种污染物空气质量监测数据,研究缺失值处理方法、效果及其影响.模拟实验表明交替最小二乘下的低秩矩阵插补算法相比于其他缺失值处理方法拥有更小的均方根误差、平均百分比误差,更高的相关系数和更快的运算速度,在大规模数据集上性能更优.实证分析表明应用文本方法得到的插补值是有效且合理的,缺失值插补前后污染物浓度评估值会有±10%以内的变化,插补后的数据集更加准确和完备.本文建议在基于空气质量监测数据研究时应先采用本文中的缺失数据处理方法,对监测数据中存在的缺失数据进行插补,提高研究所使用监测数据的完整性,保证相关计算结果的准确性和有效性.

监测数据；大数据处理；缺失值处理；矩阵填充；实证研究

我国2016年实施的《环境空气质量标准 (GB3095)》(简称“标准”)中对污染物监测数据的有效性做出明确规定,一天24h中有至少20h以上数据时,计算SO2、NO2、CO、PM2.5和PM10的日均浓度值才是有效日均数据,O3监测数据则要求每连续8h中至少有6h数据时才为有效数据.但在监测设备的日常运行中,由于某些不可预期因素(如服务器宕机、网络中断、设备故障等)导致监测数据缺失.目前国家公开发布的空气质量监测数据以小时数据为最小颗粒度,小时数据缺失会对后续日均值、月均值、年度均值、超标率、二级标准天数等指标的计算造成直接影响.2018年生态环境部印发的《城市环境空气质量排名技术规定》[1](简称“规定”)中指出SO2、NO2、PM2.5、PM10的评价浓度为日均浓度,O3的评价浓度为日最大8h平均值的90%分位数,CO的评价浓度为日均浓度的95%分位数,不符合有效性规定的数据不能参与计算,为空气质量监测数据的计算提供了标准.大规模空气质量监测数据是进行污染物时空分布规律研究的基础数据,目前大部分研究均基于中国环境监测总站发布的连续在线监测数据[2-8],数据的缺失和不同的缺失处理方法会对研究结果产生一定影响[9],但空气质量监测数据中数据缺失的影响究竟有多大,使用何种缺失处理方法更加可靠,这方面的研究还非常有限,因而研究如何更加客观、科学的处理大规模环境监测数据中缺失问题具有重要的现实应用价值.

目前国内有关环境监测数据缺失问题的研究主要集中在制度建设和管理规范方面,如建立外场监测和实验室分析的两级质量保证体系[10],通过开展专项质控工作提升监测数据质量[11],加强对生态环境监测机构的监管提升数据质量[12],通过建立从业人员监管制度确保数据质量[13],以及对国外经验的总结和借鉴[14],这些研究从体制机制的角度研究如何提升监测数据质量,但缺少对具体现实具体问题的探讨,尤其是存在大规模数据缺失情况下该如何处理,用什么方法处理,处理后的影响如何等问题还鲜有研究.国际上环境监测数据的缺失问题一直以来都是研究者非常关注的问题之一,很多缺失值处理方法也被应用于空气质量监测数据处理和研究中,如最近邻算法[15]、EM算法[16]、线性回归[17]、简单插补[18-20]、多重插补[18,21]、最小核范数[22]和低秩矩阵插补[23-24]等,多方法对比研究[21,24]发现多重插补方法和低秩矩阵方法在数据缺失较大的情况下更有优势,能够产生偏差更小的插补值来替代缺失值.以往研究对象面向的是少数监测站点和较短数据序列,现实中由于监测手段快速改进,空气质量监测数据已经出现爆发式增加,监测点数量和数量量都达到很大规模,如何处理海量环境数据中的缺失问题,已经成为越来越需要密切关注的问题.本文基于全国空气质量国控点的小时级监测数据,利用低秩矩阵插补方法处理海量监测数据中大量缺失的问题,该方法在保证插补精度的同时能够大幅度降低大规模数据处理所需时间,得到的插补值服具有较高有效性.

1 模型方法

在缺失值处理方法中,简单插补和最近邻算法方法最简单,但处理效果较差,EM算法只适用于分布为多元正态分布的数据,线性回归、多重插补虽然效果较好但计算量巨大,无法适用于大规模缺失处理.本文使用交替最小二乘下的低秩矩阵插补(Low Rank SVD via Alternating Least Square, softImpute- ALS)[25]算法,其是在低秩矩阵插补方法[26-27]基础上为解决大规模数据集处理而提出的.低秩矩阵插补方法最初在Netflix竞赛中被提出,用于插补电影评分矩阵中的缺失值,实现电影推荐的目的,因为其在大规模数据集上的优异性能而备受关注.

基本思想是在原始存在缺失值的矩阵基础上进行重建,即对矩阵中的缺失值进行填充,并保证填充后的完整矩阵与原始矩阵的秩相同.给定数据集,且中存在缺失值,由已观测值的下标构成集合W,那么softImpute-ALS算法的目标是求解以下优化问题:

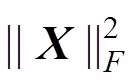
步骤1,初始化矩阵=,其中´r为随机生成且列正交,´r为单位矩阵.初始化矩阵=,其中´r=0.

步骤2,固定矩阵,通过优化式(2)来更新矩阵,

步骤3,固定矩阵,在第二步中交换矩阵和,使用同样的方法更新矩阵和矩阵.

步骤4,重复步骤2和步骤3,直到达到收敛条件.

步骤5,计算=´,并对矩阵进行SVD分解,有=R.最终输出结果、¬和,=diag[(1-)+,…,(-)+],以及填充后的矩阵*.

2 数据介绍与分析

2.1 数据介绍

本文研究数据来自中国环境监测总站实时发布的全国367个城市,1654个国控监测点自2016年1月1日到2021年7月31日的6种空气污染物小时浓度监测数据,共计48912h,理论上如果每个监测点的每种污染物在每个小时都有监测数据的话,那么监测数据总量为4.2亿条,但由于各种原因导致数据出现缺失(即空值),缺失数据总计814万条.本文将缺失数据总量除以理论数据总量定义为数据缺失率,那么国控点监测数据的总体缺失率为19.3‰.数据中不同污染物缺失率并不相同,SO2缺失率为9.6‰,NO2为10.9‰,CO为13.1‰,O3为14.4‰,PM2.5为15.3‰,PM10为52.4‰,PM10缺失率最高,而SO2缺失率最低.

2.2 监测点数据缺失情况

不同监测点的缺失情况存在很大差异(表1),以PM2.5为例,缺失最严重的监测点的缺失率达到331.7‰,即三分之一的数据因各种原因缺失,致使监测点数据有效性大打折扣,在使用该数据进行分析时,可能会导致较大误差.因而有关部门在使用空气质量监测数据时,会对监测数据进行校验,但当前大部分研究中所使用的公开数据集往往是未经过校验处理的,其中就存在大量缺失值,缺失值对相关计算结果的影信息响究竟有多大,还没有被深入讨论.

表1 不同污染物的监测点数据缺失统计(‰)

2.3 缺失机制分析

数据缺失的内在机理可以划分3种类型[28],分别是完全随机缺失(MCAR)、随机缺失(MAR)和非随机缺失(MNAR).其中MAR相比于MCAR更加常见和符合现实,也是缺失值处理方法最主要的研究对象.MAR指仅在某个特定的组内缺失值是随机产生的,而不同组之间不一定是随机的.对应到空气质量数据的缺失机制,由于不同污染物缺失率不同,不同监测点的缺失率也有很大差异,显然污染物缺失并不是完全随机的,而仅在特定监测点和污染物条件下是可以视作是随机缺失的.此外,空气质量是连续在线监测模式,如果因设备故障而导致数据缺失的话,数据往往会连续缺失一定时段直到设备故障排除.表2显示,三分之二左右的缺失间隔仅为1,说明大部分情况下缺失值是偶然出现.但也有三分之一左右的缺失间隔大于1,缺失在10h以上的情况占比达到3%以上,这很可能是出现明显的设备故障,需要一定的维修时间.其中PM2.5最大连续缺失200h,PM10最大连续缺失196h,SO2最大连续缺失192h,NO2最大连续缺失197h,O3最大连续缺失189h,CO最大连续缺失191h.研究表明随着缺失间隔的增大,使用简单缺失值处理方法(如均值填充等)的有效性不断下降[29-30],更加需要有效方法来处理大规模缺失的情况,而softImpute-ALS方法在严重缺失的情况也能有很好的插补性能[25],因而适用于处理空气质量监测中的缺失值.

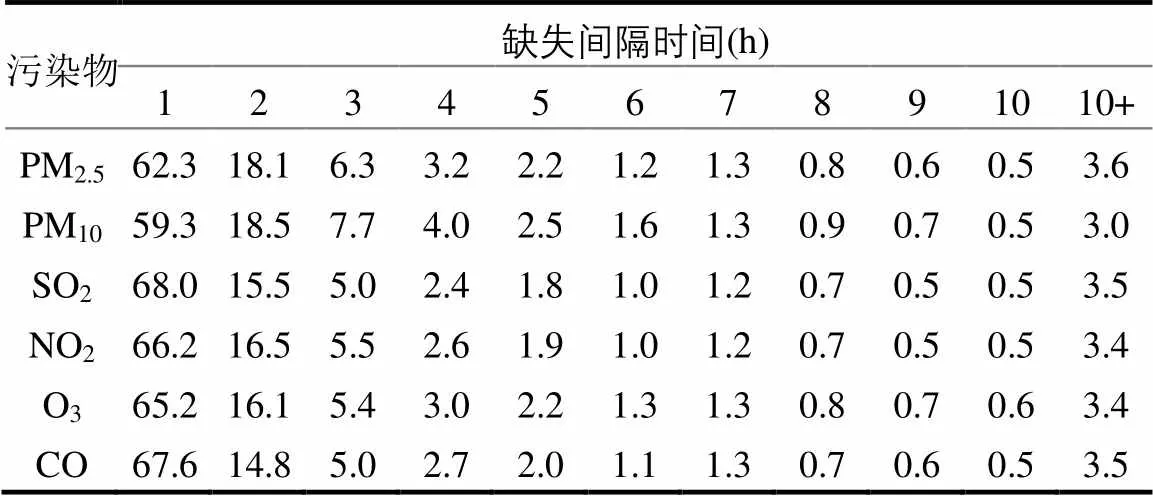
表2 不同污染物缺失间隔占比(%)

3 模拟实验

3.1 实验设计

为考察softImpute-ALS方法在大规模缺失数据集上的优劣,需要构造相应数据集,并计算各种缺失值处理方法在不同评估指标上的表现.因此,本文通过以下模拟方案生成算法评估数据集.方案包括四个步骤:(1)抽取可能产生缺失的污染物,抽取概率为不同污染物的缺失值数量占全部缺失值数量的比例;(2)抽取可能产生缺失的监测点,抽取概率为污染物下,监测点缺失值数量占全部该污染物全部缺失值数量的比例;(3)随机抽取可能产生缺失的时间点,即该时刻开始出现缺失值;(4)抽取产生缺失的间隔长度,抽取概率为表2中缺失间隔对应的占比;(5)记录缺失值的下标(,,,),并将原始数据中相同下标的数据标记为缺失值.通过以上四个步骤,在模拟真实缺失机制前提下,本文生成得到两份数据集,一份为原始数据集,一份是标记了缺失值的数据集.接下来,本文对数据集运用不同缺失值方法,通过考察其还原数据集的程度来评估方法的优劣.

3.2 评估指标

使用的评估指标有均方根误差(RMSE)、平均绝对百分比误差(MAPE)和皮尔逊相关系数().RMSE指标用于测度缺失值和插补值之间绝对偏差的大小,RMSE越小说明插补值约接近原始值.MAPE指标用于测度缺失值和插补值之间相对误差的大小,MAPE可以比较消除量纲后偏差的大小.指标用于测度变量间线性相关关系,指标值介于-1到1之间,越大说明缺失值与插补值之间相关性越高,二者拟合效果越好.不妨令模拟数据中观测值下标集合为W,则缺失值下标构成的集合是W的补集记为Wc,为原始的模拟数据,为缺失值填充后的数据,为缺失值数量,则评估指标的具体计算公式为:

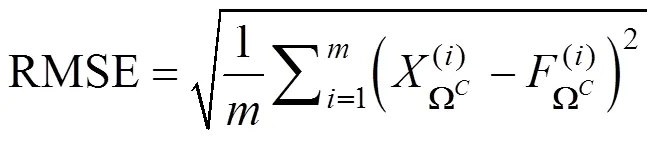
3.3 实验结果

选择简单填充、线性插值、向前填充、最近邻插补、EM插补、多重插补方法作为对比,比较这些方法和softImpute-ALS在相同数据集上,模拟真实缺失机制下在RMSE、MAPE、和运算时间(time)上的表现.重复实验10次,最终结果为10次实验的平均值,实验使用平台配置为2.2GHz的CPU和16G DDR3内存,实验结果如表3所示(1)softImpute-ALS插补后的值在RMSE、MAPE两个指标上均表现最小,说明softImpute-ALS能够更加准确的插补缺失值,同时softImpute-ALS的插补值与真实值有更高的相关性,其他方法中只有最近邻填充能够与softImpute-ALS方法在准确度方面更为接近.(2)时间消耗方面,softImpute-ALS对不同污染染处理时间介于160～180s之间,虽然相比于简单填充、线性插值和向前填充耗时显著增加,但相比最近邻方法无疑有巨大的优势,最近邻方法处理每种污染的用时在3h左右,是softImpute-ALS的70倍以上.实验表明softImpute-ALS方法相比于其他方法有更好的准确度,并且处理时间可控,因而softImpute-ALS方法在处理大规模缺失数据方面具有显著的优势.

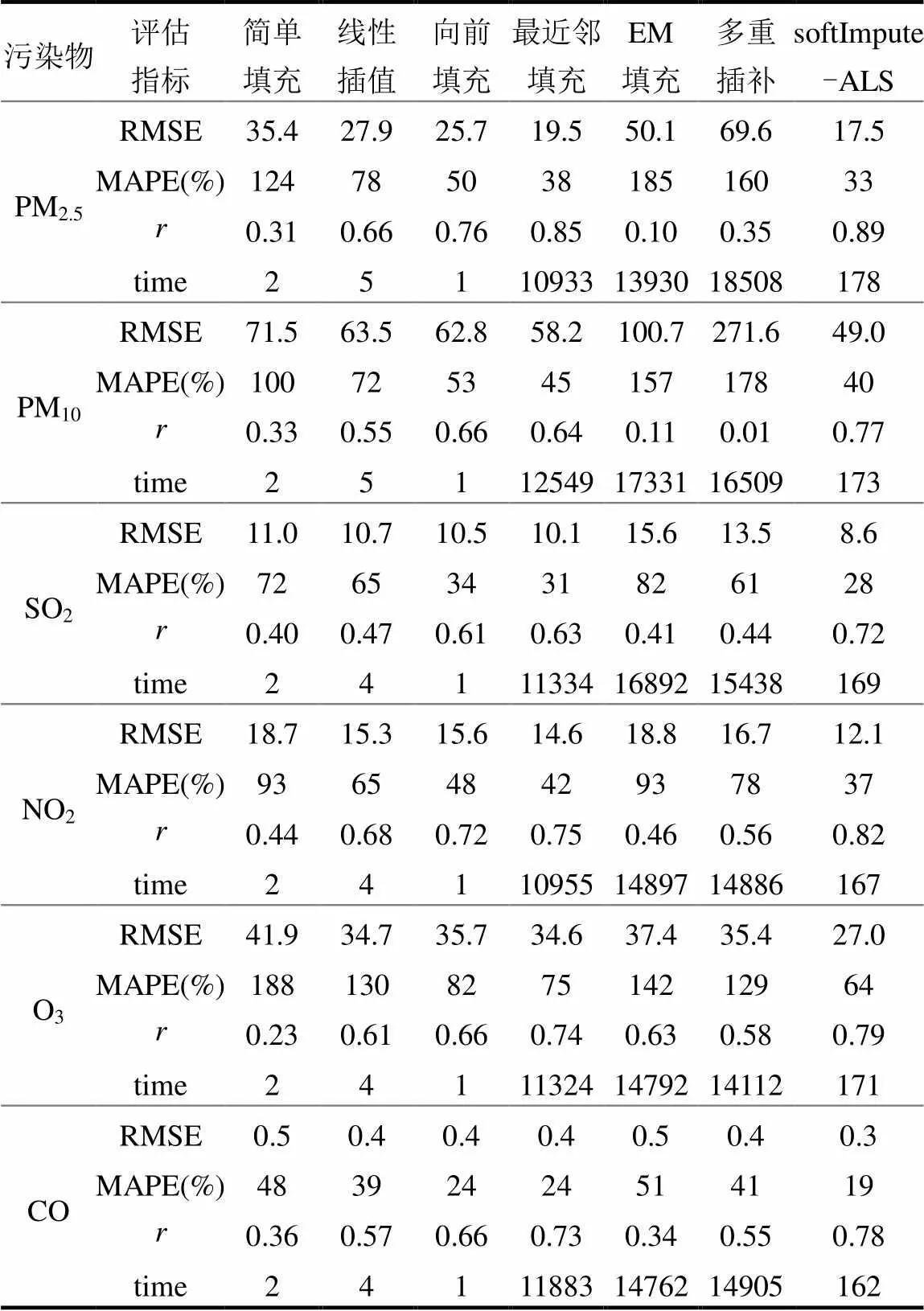
表3 不同缺失值插补方法比较

4 实证分析

4.1 数据有效性分析

“规定”中指出“SO2、NO2、PM10、PM2.5的评价浓度为评价时段内日均浓度的平均值,O3的评价浓度为评价时段内日最大8h平均值的第90百分数,CO的评价浓度为评价时段内日均浓度的第95百分位数”的计算方法,同时指出城市的日均浓度首先要“计算各监测点位日均浓度,然后计算算数平均值得到城市日均浓度,再由此计算你评价时段内城市均值或特定百分位数”.各监测点位的日均浓度由该日24h监测值求平均而得,在“标准”中规定每日至少有20h的平均浓度值”才能计算24h均值,否则该日数据无效.

依据以上标准,统计每个监测点每日浓度并判断其有效性,然后计算每个城市平均浓度及其有效性.研究发现,从2016年1月1日至2021年7月31日共计2038d,监测点有效天数最大是O­3的1892d,意味着该监测点有多达146d未满足有效性要求.同时,整体上有超过50%左右的监测点数据有效时间介于1655～1840d之间,无效时间在198～383d之间(表4),可见由于存在大量缺失值,导致数据有效时间显著减少,每日污染浓度的分析结果可能存在较大偏差.“规定”中并未指明在城市某个或某几个监测点当日数据无效情况下,如何计算该城市当日污染物平均浓度,而只是笼统的给出“当任何一项污染物不满足上述有效性规定且任何一项污染物浓度超过二级标准限值时,以城市当日污染物浓度最高点位的数据”的规定,这样以“最大值”替代的处理方式对于研究污染物时空分布显然并不适用,更加合理的方式是利用模型算法对缺失值进行准确的估计.

表4 全部国控监测点不同污染物监测数据有效时间统计

4.2 缺失值影响分析

由于“规定”中没有明确给出监测点当日数据无效的处理方法,当监测点当日数据无效时,分2种情况分别讨论.第1种情况,如果一个城市当日有一个或多个监测点数据无效,则当日该城市数据也无效;第2种情况,如果监测点当日数据无效,则取该监测点当日浓度最高值作为当日有效数据.在这2种情况下,缺失值均对后续当日城市污染物浓度的计算均会产生重大影响.

在第1种情况下,以生态环境部发布的《2021年8月全国城市空气质量报告》[31]中空气质量相对较差的20个城市为例,分析这些城市由于数据缺失导致的无效数据问题.表5显示,在过去5年多中,这20个城市各种污染物平均每年的无效时间约为60d,即有将近两个月的时间按照“规定”是无效数据,以济南市PM10为例,无效时间更是达到881d,年均160d,无效时间的比例远超按小时统计的1%～5%的数据缺失率,其主要原因是每个监测点每日须满足大于等于20个有效监测数据.即使按照规定中日最大浓度替代日均值浓度的方法,也意味着这些城市每年有将近2个月的时间使用日最高浓度进行排名计算.

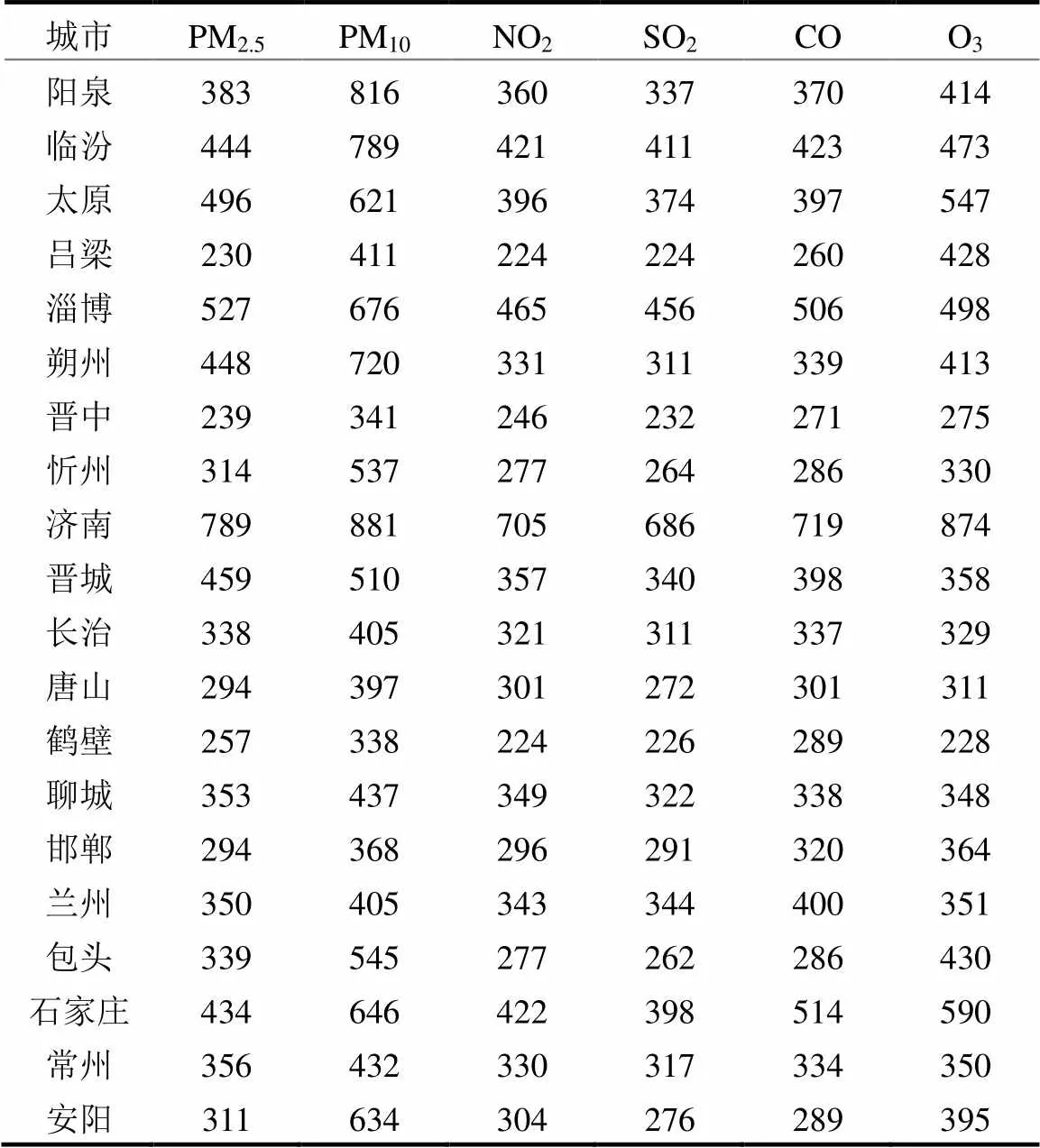
表5 空气质量排名后20城市的数据无效时间统计

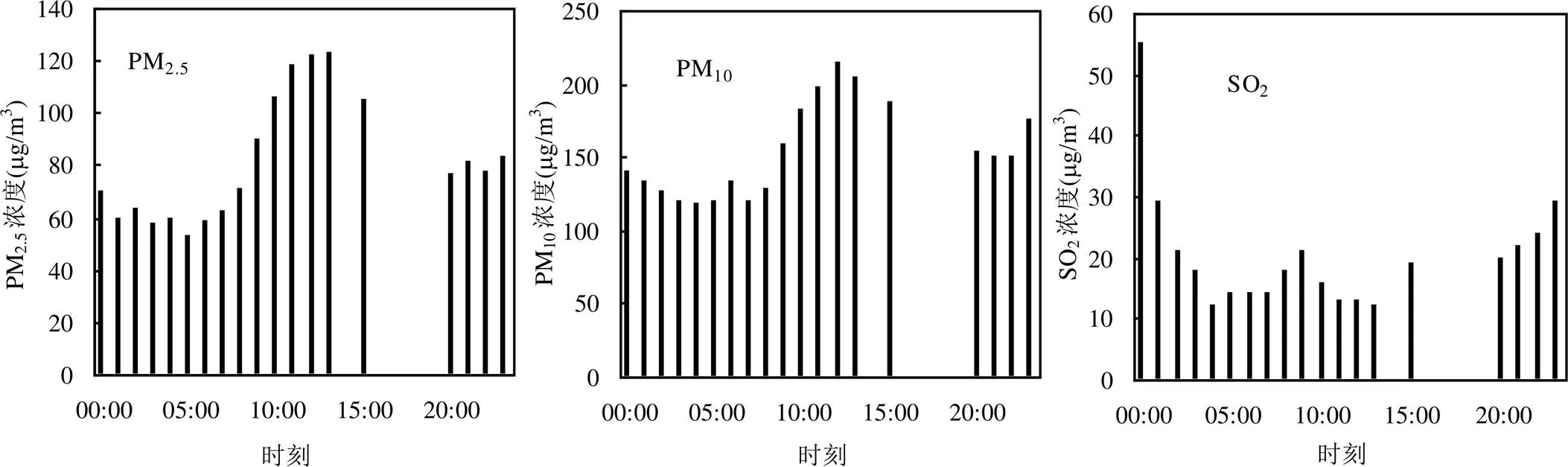
在第2种情况下,污染物浓度在一天内存在很大的波动,造成最大浓度与平均浓度之间有很大差异,最大浓度无法反映真实情况.以济南市机床二厂监测点2021年2月3日为例,当日有效监测数据恰为19个,小于20个有效监测数据的要求,缺失14:00、16:00、17:00、18:00和19:00这5个小时监测数据.图1显示一天内不同时点污染物浓度存在很大差异,该监测点PM2.5最大浓度123mg/m3,19个小时平均值为81mg/m3,相差52%,PM10最大浓度214mg/m3,19小时平均值153mg/m3,相差40%,SO2最大浓度55mg/m3,19小时平均值20mg/m3,相差172%,NO2最大浓度69mg/m3,19小时平均值40mg/m3,相差75%, O3最大浓度87mg/m3,19小时平均值59mg/m3,相差47%,CO最大浓度1.3mg/m3,19小时平均浓度0.9mg/m3,相差41%.“规定”中的“最大浓度替代”与实际情况存在很大差异,不能反应污染物的真实浓度,仅仅是在计算层面对缺失数据进行惩罚性处理.当存在某些不可抗拒因素导致数据缺失时,这样的处理方法并不合理,而应当采取更科学和可靠的插补方法,最大程度近似或还原真实值.

4.3 插补值有效性分析

应用softImpute-ALS方法对全国国控点空气质量数据进行缺失值的插补处理,未验证插补值的有效性,为与上文保持一致,选取济南市机床二厂和科干所两个监测点来验证插补值的有效性.具体方法是分别计算两个监测点每种污染物在剔除缺失值后的数据、插补值数据、插补缺失值后的数据这3个数据集上的相关系数,并且绘制散点图(图2)来分析插补值的有效性与合理性,即如果2个监测点在3个数据集的相关系数比较接近,则说明插补值也符合原有数据规律,插补方法是有效的.

由图2可见,插补值与剔除缺失的数据在污染物相关关系上是一致的,插补前两个监测点PM2.5的相关系数是0.93,插补后的相关系数是0.94,缺失值处理方法得到的插补值也服从监测点间相关的规律.此外计算济南市其他任意2个监测点之间在3个数据集上的相关系数,均得到大于0.9的相关系数.

4.4 实证结果分析

应用softImpute-ALS方法对全国国控点空气质量数据进行缺失值的插补处理,并依据“规定”中城市浓度计算标准,分析缺失值插补后的城市浓度值和排名的变化情况.以2021年7月为例,分别对168个城市分别计算PM2.5,PM10,SO2,NO2,CO-95%分位数,O38h-90%分位数的浓度值及其排名.生态环境部在发布城市空气质量排名时会对监测数据进行校验,校验后数据质量要优于实时监测数据,但校验后数据并未公开发布,本文实证分析部分基于中国环境监测总站实时在线监测数据,仅用于分析缺失值处理方法对计算结果的影响,说明在使用公开空气质量监测数据时对缺失值处理的必要性.

4.4.1 全国城市PM2.5浓度缺失值插补前后计算结果 20个城市中有18个相同的城市,说明缺失值插补前后排名总体上一致,但局部排名有明显的变化.主要原因是2021年7月所有城市PM2.5月度均值总体较低,并且不同城市的监测值相差非常小,即计算值的微小变化会导致排名的较大变化.缺失高浓度监测值会显著提升城市排名,而缺失低浓度监测值会显著降低城市排名,此时缺失值的处理方法会对城市排名产生关键影响.

表6显示,不同城市缺失率显著不同,最高缺失率5.2%,最低缺失率0.8%,而“规定”中并没有明确监测点小时监测数据缺失处理方法,只是给出“以城市污染物浓度最高点位的数据,统计当日污染物浓度排名”,这样的处理方式是不合理的,也没有考虑污染物在一天的周期性变化特征.使用合理插补方法后,PM2.5月度浓度均值变化在-7.8%～ 10.1%之间,基于公开在线监测数据进行研究时,应当采取合理、可靠的缺失值处理方法对缺失值进行插补,减少缺失值对最终计算结果的影响.

表6 缺失值插补前后城市PM2.5排名比较

注:(1)原排序中相同序号按照城市出现前后的倒序排列;(2)插补前后变动计算公式为:(插补后-插补前)/插补前.

4.4.2 全国城市PM10浓度缺失值插补前后计算结果 排名后20城市中有16个相同城市,PM10缺失率从0.9%～6.0%之间,排名变化较大的是石家庄市,PM10的月度均值从47mg/m3下降至44mg/m3,从原排名163名上升至152名,上升11名,而运城市的PM10的月度均值从42mg/m3上升至45mg/m3,排名也从150名下降至157名.

表7 缺失值插补前后城市PM10排名比较

注: (1)原排序中相同序号按照城市出现前后的倒序排名;(2)插补前后变动计算公式为:(插补后-插补前)/插补前

4.4.3 全国城市SO2浓度缺失值插补前后计算结果 排名的后20城市全部相同,SO2缺失率从1.4%～ 5.5%之间.由于SO2月度均值差异较大,插补后排名与原排名的最后7名次序均相同,但在之后排名次序显著不同,即当污染物月度均值有较大差异时,缺失值插补对排名影响较小,但如果污染物月度均值比较接近时,缺失值插补会显著影响排名情况.

4.4.4 全国城市NO2浓度缺失值插补前后计算结果 排名后20城市中有17个相同城市,NO2缺失率为1.2%～5.4%之间.与SO2排名类似,NO2月度均值差异较大,插补后排名与原排名的最后5名次序均相同,其他城市的排名情况均有所变化,但排名上升和下降幅度较小.

表8 缺失值插补前后城市SO2排名比较

注:(1)原排序中相同序号按照城市出现前后的倒序排名;(2)插补前后变动计算公式为:(插补后-插补前)/插补前

表9 缺失值插补前后城市NO2排名比较

注:(1)原排序中相同序号按照城市出现前后的倒序排名;(2)插补前后变动计算公式为:(插补后-插补前)/插补前.

表10 缺失值插补前后城市CO日均值95%分位数排名比较

注:(1)原排序中相同序号按照城市出现前后的倒序排名;(2)插补前后变动计算公式为:(插补后-插补前)/插补前.

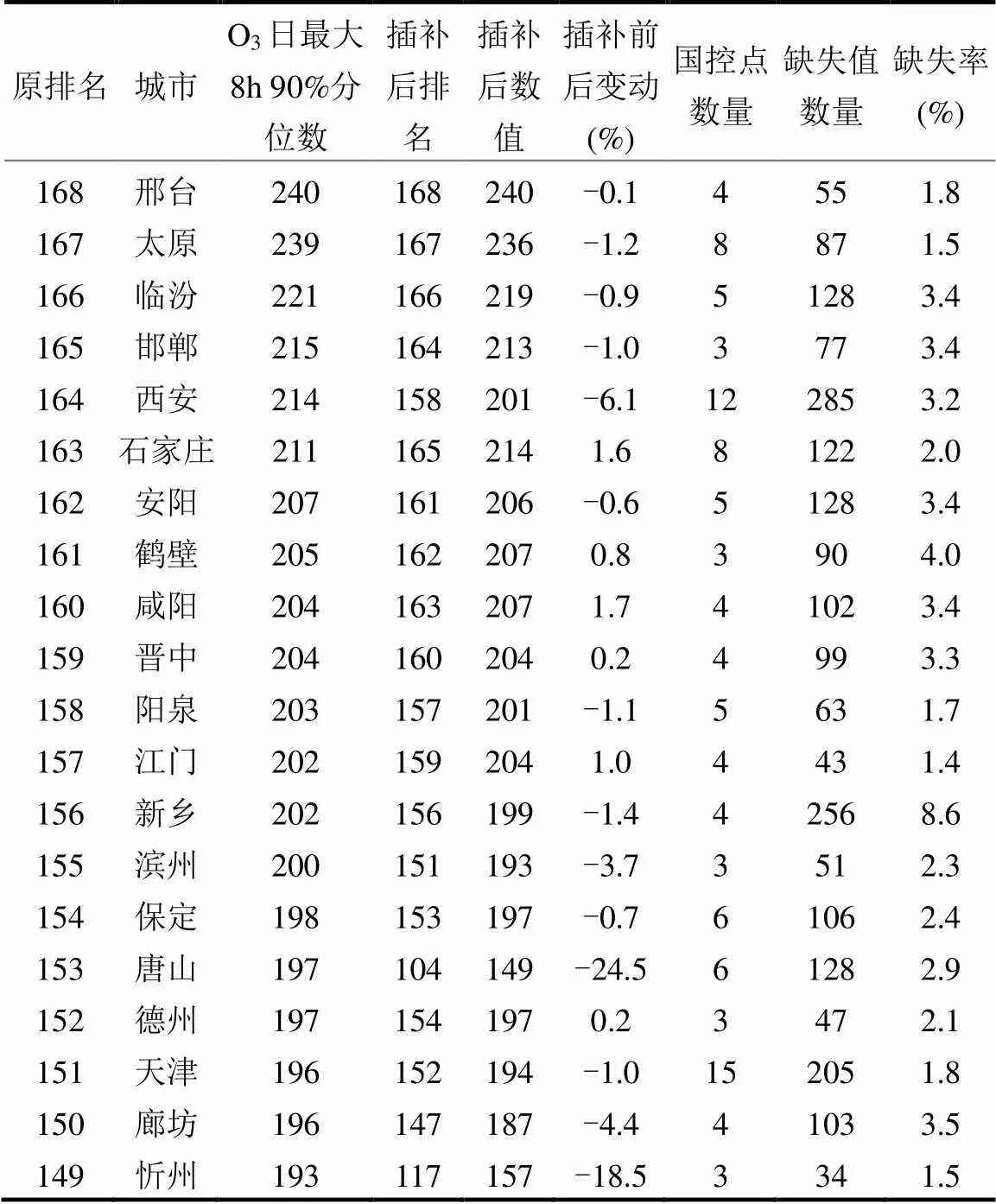
表11 缺失值插补前后城市O3日最大8h90%分位数排名比较

注:(1)原排序中相同序号按照城市出现前后的倒序排名;(2)插补前后变动计算公式为:(插补后-插补前)/插补前.

4.4.5 全国城市CO日均值95%分位数和O3日最大8h 90%分位数 通过CO日均值95%分位数(表10)与O3日最大8h 90%分位数(表11)的排名比较,在数值较为接近时,城市排名会受到缺失值的显著影响,缺失值如何处理将直接影响城市排名前后次序.新余、承德、唐山、运城和忻州这5个城市CO日均值在插补前后变动均超过10%,其中运城和忻州的分别从插值前的157名和151名,在插值后变为138名和121名,提升20和30名,可见缺失值对城市评价浓度具有显著影响.

5 结论

研究表明数据缺失会对计算结果造成显著影响程度,尤其是进行日尺度和城市尺度的统计分析,本研究对于提升监测数据完整率和分析结果准确率方面具有一定的现实意义.基于softImpute-ALS方法,对2016年以来的全国国控点小时级的大规模监测数据进行缺失值插补处理,模拟实验表明本文所使用方法能够得到较好的估计值,RMSE、MAPE和相关系数均优于其他缺失值常规处理方法,同时缺失值估计过程具有较快的处理速度.实证分析结果表明,缺失值插补前后6种污染物评价浓度会有±10%左右的变化,同时监测点的缺失值数量越多,缺失值插补前后浓度的计算值变化也越大,越有必要进行缺失值处理.建议在基于公开的大规模空气质量监测数据进行空气质量研究时,首先应采用softImpute-ALS方法对监测数据进行缺失值处理,得到更加准确的估计值,提升监测数据完整率,最大程度减少缺失值可能导致的结果有偏问题,提升相关研究结果的准确性和可靠性.

[1] 中华人民共和国生态环境部.城市环境空气质量排名技术规定[R]. 2018.

Ministry of Ecology and Environmental of People's Republic of China. Technical regulations for air quality ranking of cities[R]. 2018.

[2] Deng Q, Yang K, Luo Y. Spatiotemporal patterns of PM2.5in the Beijing–Tianjin–Hebei region during 2013～2016 [J]. Geology, Ecology, and Landscapes, 2017,1(2):95-103.

[3] Li L, Wu A H, Cheng I, et al. Spatiotemporal estimation of historical PM2.5concentrations using PM10, meteorological variables, and spatial effect [J]. Atmospheric Environment, 2017,166:182-191.

[4] Hu M, Wang Y, Wang S, et al. Spatial-temporal heterogeneity of air pollution and its relationship with meteorological factors in the Pearl River Delta, China [J]. Atmospheric Environment, 2021,254:118415.

[5] Li L, Zhang J, Meng X, et al. Estimation of PM2.5concentrations at a high spatiotemporal resolution using constrained mixed-effect bagging models with MAIAC aerosol optical depth [J]. Remote Sensing of Environment, 2018,217:573-586.

[6] Shen Y, Zhang l, Fang X, et al. Spatiotemporal patterns of recent PM2.5concentrations over typical urban agglomerations in China [J]. Science of the Total Environment, 2019,655:13-26.

[7] Zhao S, Yin D, Yu Y, et al. PM2.5and O3pollution during 2015～2019 over 367 Chinese cities: Spatiotemporal variations, meteorological and topographical impacts [J]. Environmental Pollution, 2020,264:114694.

[8] Li K, Jacob D J, Liao H, et al. A two-pollutant strategy for improving ozone and particulate air quality in China [J]. Nature Geoscience, 2019, 12(11):906-910.

[9] Liu J, Li W, Wu J. A framework for delineating the regional boundaries of PM2.5pollution: A case study of China [J]. Environmental Pollution, 2018,235:642-651.

[10] 张 烃,董树屏,滕 曼,等.区域大型环境空气综合观测中外场观测与实验室分析数据质量控制研究[J]. 环境科学研究, 2019,32(10): 1664-1671.

Zhang T, Dong S P, Teng M, et al. Quality assurance of field observation and laboratory analysis in regional large scale ambient air joint monitoring campaigns [J]. Research of Environmental Sciences, 2019,32(10):1664-1671.

[11] 师耀龙,吕怡兵,肖建军.夏季重大活动期间O3监测数据质量提升方法研究[J]. 中国环境监测, 2020,36(2):10-14.

Shi Y L, Lyu Y B, Xiao J J. Data quality control method of ozone monitoring during the guarantee for major events in summer [J]. Environmental Monitoring in China, 2020,36(2):10-14.

[12] 师耀龙,陈传忠,魏俊山,等.加强生态环境监测机构监督管理的思考与分析[J]. 环境保护, 2018,46(23):56-60.

Shi Yao-long, Chen Chuan-zhong, Wei Jun-shan, et al. The current situation and problem analysis of environmental monitoring organizations' supervision and administration [J]. Environmental Protection, 2018,46(23):56-60.

[13] 刘 媛,彭 溶,张 驰,等.环境监测从业人员监管制度研究[J]. 环境保护, 2018,46(18):33-35.

Liu Y, Peng R, Zhang C, et al. Research on supervision system of environmental monitoring practitioners [J]. Environmental Protection, 2018,46(18):33-35.

[14] 师耀龙,杨 婧,柴文轩,等.美国环境空气监测数据质量核查工作的经验与启示[J]. 中国环境监测, 2017,33(3):8-14.

Shi Y L, Yang J, Chai W X, et al. Experience and illumination of data quality assessment system for ambient air monitoring in the United States [J]. Environmental Monitoring in China, 2017,33(3):8-14.

[15] Rumaling M I, Chee F pien, Dayou J, et al. Missing value imputation for PM10concentration in Sabah using nearest neighbour method (NNM) and expectation-maximization (EM) algorithm [J]. Asian Journal of Atmospheric Environment, 2020,14:62-72.

[16] Junger W L, Ponce D E Leon A. Imputation of missing data in time series for air pollutants [J]. Atmospheric Environment, 2015,102:96- 104.

[17] Larsen L C, Shah M. A context-intensive approach to imputation of missing values in data sets from networks of environmental monitors [J]. Journal of the Air & Waste Management Association (1995), 2016,66(1):38-52.

[18] Junninen H, Niska H, Tuppurainen K, et al. Methods for imputation of missing values in air quality data sets [J]. Atmospheric Environment, 2004,38(18):2895-2907.

[19] Hadeed S J, O’rourke M K, Burgess J L, et al. Imputation methods for addressing missing data in short-term monitoring of air pollutants [J]. Science of The Total Environment, 2020,730:139140.

[20] Real C, Ángel Fernández J, Aboal J R, et al. Substituting missing data in compositional analysis [J]. Environmental Pollution, 2011,159(10): 2797-2800.

[21] Gómez-Carracedo M P, Andrade J M, López-Mahía P, et al. A practical comparison of single and multiple imputation methods to handle complex missing data in air quality datasets [J]. Chemometrics and Intelligent Laboratory Systems, 2014,134:23-33.

[22] Chen X, Xiao Y. A novel method for air quality data imputation by nuclear norm minimization [J]. Journal of Sensors, 2018,2018: e7465026.

[23] Moshenberg S, Lerner U, Fishbain B. Spectral methods for imputation of missing air quality data [J]. Environmental Systems Research, 2015,4(1):26.

[24] Liu X, Wang X, Zou L, et al. Spatial imputation for air pollutants data sets via low rank matrix completion algorithm [J]. Environment International, 2020,139:105713.

[25] Hastie T, Mazumder R, Lee J D, et al. Matrix completion and low-rank SVD via fast alternating least squares [J]. 36.

[26] Candès E J, Recht B. Exact matrix completion via convex optimization [J]. Foundations of Computational Mathematics, 2009, 9(6):717.

[27] Candès E J, Tao T. The power of convex relaxation: near-optimal matrix completion [J]. IEEE Transactions on Information Theory, 2010,56(5):2053-2080.

[28] Buuren S van. Flexible imputation of missing data [M]. 2nd edition. Boca Raton: Chapman and Hall/CRC, 2018.

[29] Liu Y, Dillon T, Yu W, et al. Missing value imputation for industrial IoT sensor data with large gaps [J]. IEEE Internet of Things Journal, 2020,7(8):6855-6867.

[30] Velasco-Gallego C, Lazakis I. A novel framework for imputing large gaps of missing values from time series sensor data of marine machinery systems [J]. Ships and Offshore Structures, 2021,10.1080/ 17445302.2021.1943850.

[31] 中华人民共和国生态环境部.2021年8月全国城市空气质量报告[R]. 2021.

Ministry of Ecology and Environmental of People's Republic of China. Air quality reports for cities in China[R]. 2021,8

致谢：本研究受中国人民大学“双一流”跨学科重大创新规划平台—生态文明跨学科交叉平台支持.

Research on the missing value methods for large-scale online air quality monitoring data.

ZHANG Bo, SONG Guo-jun*

(School of Environment and Natural Resources, Renmin University of China, Beijing 100872, China)., 2022,42(5)：2078～2087

Large scale online air quality monitoring data is the basis for air quality research, but there were lots of missing data in large scale online data. In this study, we compared several methods that dealing with the missing values and its impact on the city’s ranking of air quality base on the hourly monitoring data of 1654monitoring sites in China from 1Jan, 2016 to 31July, 2021 of 6types of air pollutants. The simulation results showed that Low Rank SVD via Alternating Least Square had smaller mean squared error, mean absolute percentage error and higher correlation coefficient compared with other traditional methods. The empirical results showed there would be 10% difference before imputation and after imputation for the missing value. The ranking would not change due to the imputation when the air quality assessed value vary greatly, and would change a lot when the assessed value was very close. The study suggested to impute missing value by using the method in this study when analysis the large-scale online air quality monitoring data.

monitoring data；big data；missing value；low rank matrix；empirical research

X323

A

1000-6923(2022)05-2078-10

张 波(1986-),男,内蒙古包头人,讲师,博士,研究方向为环境统计与建模.发表论文10余篇.

2021-10-12

中国人民大学科学研究基金(中央高校基本科研业务费专项资金资助)项目成果(22XNF016)

* 责任作者, 教授, songguojun@ruc.edu.cn