机载云平台系统中基于可靠性感知的卸载策略

郑 萍

(南昌师范学院 数学与信息科学学院，江西 南昌 330032)

0 引言

随着物联网技术的发展，智能设备生成的数据量呈指数增长。物联网设备的能量和处理能力有限，导致执行任务效率较低。针对这一问题，部分研究者提出将移动设备上的计算任务或数据传输至远程云端执行[1-2]，然而，传统的云计算传输延时较大，无法满足用户的实时需求[2-4]。移动边缘计算(Mobile Edge Computing，MEC)可以有效降低时延。然而，对于通信链路不稳定的地区，数据传输可靠性降低[5-8]。通过无人机上搭载云平台(Cloudlet)为移动用户提供边缘计算能力，有效降低网络拥塞和时延。无人机边缘计算相对于传统的边缘计算，虽然与数据源更近，但是边缘计算资源受限，因此需要合理利用能量和计算资源，满足大量用户的请求，协调多个无人机之间的计算卸载[9-12]。

近年来,MEC的任务卸载引起了研究人员的广泛关注。文献[13]研究了多用户MEC系统中高能效资源分配方案，将任务卸载和服务缓存联合优化问题转化为服务缓存和任务卸载问题，但未考虑到通信资源的分配。文献[14]利用单个无人机协助多个移动终端进行任务卸载，但无法满足多用户密集型计算任务的需求。文献[15]在系统时延约束下，建立了基于计算卸载和任务分配的联合凸优化目标，但未考虑能耗优化。文献[16]设计了多无人机下自适应任务卸载方案，但未考虑无人机飞行耗能。文献[17]将多无人机视为MEC服务器，并研究了由2层无人机组成的MEC网络的卸载问题，但是该卸载策略容易受到外部环境的影响，计算的可靠性低。文献[18]针对无人机支持的网络场景，通过轨迹优化和联合资源分配的方法提升系统能量效率，但未考虑任务卸载的时延要求。

本文提出了一种可靠性感知计算卸载解决方案。该卸载策略优化无人机的位置、终端任务的划分、通信和计算资源的分配，将卸载时延和可靠性计算问题表述为非凸混合整数非线性规划(Mixed Integer Nonlinear Programming，MINLP)问题，再将其转化为凸性函数，降低了计算的复杂度，利用基于连续凸逼近(Successive Convex Approximation，SCA)方法的低复杂度迭代算法求解。该算法可以在满足时延和可靠性的同时，最大限度地增加卸载请求的数量。

1 系统模型

图1所示为本文系统模型，由于本文分析机载云平台卸载延迟和可靠性敏感计算问题，因此将系统模型分为计算模型、通信模型、可靠性模型以及延迟模型。通过非凸MINLP的形式对机载云平台卸载延迟和可靠性敏感计算问题进行建模和公式表达。

图1 基于MEC的系统模型Fig.1 System model based on MEC

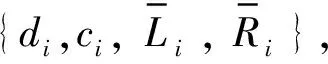
1.1 计算模型

采用数据分区模型，其中一个任务可以部分卸载并在多个无人机上并行计算，例如图像/视频处理。假设任务划分的粒度具有任意精度，并且任意2个子任务之间不存在重叠。Si={1,2,…,S}表示任务i可以创建为子任务集，最多可以创建M个子任务(即可用无人机的数量)，Sik变量表示任务i分配给子任务k∈S的大小，Sik=0意味着子任务不存在。为了提高任务i的可靠性，可以将子任务k卸载到多架无人机执行。因此，用oikj表示一个二元决策变量，其中oikj=1表示将任务i的子任务k卸载给UAVj，否则oikj=0。将任务i的子任务k卸载给机载云平台j时，计算分配的资源量为fikj≥0 Hz，但不能超过机载云平台的计算能力Fj。通过一个二元决策变量ai表示任务i是否允许被卸载至其他无人机上执行。综上所述，本模型满足以下约束条件：

(1)

sik≤ai,∀{i,k}∈{N,S}，

(2)

oikj≤ai,∀{i,k}∈{N,S,M}，

(3)

(4)

式(1)保证当任务被允许时子任务部分之和等于1。式(2)和式(3)确保未被允许的子任务为空且被忽略。式(4)保证一个已被卸载的子任务被允许。

1.2 通信模型

假设在一个开放的环境中，终端和无人机之间的通信信道由视距(Line-of-Sight，LOS)传播链路所主导。因此，UEi和UAVj之间的信道增益为：

hij(θij)=θijgo，

(5)

(6)

式中，θij和go分别表示参考距离为1 m时的路径损耗系数和信道功率增益。

假设一个带宽为BMHz的共用无线电频谱。由于任务输出大小通常比任务输入小得多，因此本文忽略了下行通信。子任务的卸载率为：

(7)

式中，Pij为UEi到UAVj的发射功率；N0为噪声功率谱密度；bij为UEi和UAVj之间通信分配的带宽。

1.3 可靠性模型

云计算系统的可靠性是衡量系统能够提供不中断的无故障服务的稳定程度。即可靠性定义为：在某种规定的条件下，系统能够在约定的时间范围内稳定提供无故障服务的能力。本文利用平均故障间隔时间和从历史故障和维修记录中得到的平均修复时间来表示机载云平台j的可靠性，用φj表示。假设通信链路可靠，LOS链路提高了上行传输效率。为了保证任务的可靠性，采用冗余的方式，即在多架无人机上并行传输和计算一个子任务,保证任务i∈N可靠性的条件如下：

(8)

1.4 延迟模型

完成任务i的端到端时延取决于最后一个子任务完成的时延，因此每个被卸载的子任务的总时延必须遵守任务延迟阈值，满足约束条件：

(9)

(10)

式中，rikj为决策变量，表示子任务k在UEi与UAVj之间进行传输的卸载率Rij(θij,bij)的部分。式(9)确保满足终端最大时延要求，其中时延由上传时延和计算时延组成；式(10)确保子任务满足最大任务卸载率。

1.5 问题制定

通过优化无人机的位置、无人机子任务的数量和大小、无人机与子任务之间的关联以及分配的子任务无线电和计算资源，在满足终端所需的延迟和可靠性的同时，最大限度地增加可执行任务数量。本文采用集中式方法，控制器离线进行优化程序。由于终端的任务请求在一段时间内重复出现，并在操作运行之前收集，因此无人机的位置在整个卸载过程中可以进行优化，移动终端定期进行任务卸载。另外，可通过重新分配无线电和计算资源来处理请求中的变化。将计算卸载问题构造成非凸性MINLP函数，其表达式如下：

(11)

s.t.(1),(2),(3),(4),(8),(9),(10)

(12)

(13)

(14)

(15)

式(12)是式(6)的简化公式，降低了问题的复杂性。约束条件式(13)保证所有执行卸载任务满足无人机云的计算能力，约束条件式(14)表示任务的通信带宽满足系统无线电带宽B，约束条件式(15)为完整性和非负条件。

2 卸载算法

由于式(11)及其约束条件的高复杂性和非凸性，将其转换为更易于处理的形式，并使用低复杂性的基于SCA的迭代算法来求解问题的近似解。首先将非凸约束凸化为近似式(11)。然后利用基于SCA的二阶锥规划(Second Order Cone Programming，SOCP)算法进行迭代求解直到收敛。

2.1 式(8)凸化

引入松弛变量α={αik≥0,i∈N,k∈S}，将约束条件式(8)改写为：

(16)

对式(16)两边取自然对数，并利用它的性质将其等价改写为:

(17)

(18)

(19)

(20)

式中，αik≥0为新的松弛变量；ε为趋于零的正数。

2.2 式(9)近似

本文引入松弛变量β={βik≥0,∀i∈N,k∈S}，将式(9)等价改写为：

(21)

(22)

(23)

将约束条件式(22)改写为以下线性形式：

(24)

2.3 式(12)的近似

(25)

将约束条件式(12)改写为以下形式:

(26)

2.4 混合整数SOCP问题变换

非凸型约束条件线性化后，将问题进一步转化为SOCP形式，可以有效提高求解速度和精确度。本文利用二次锥近似法将约束条件式(10)改写为：

(27)

式中，km={kik≥0，i∈N，j∈M}为一个新的松弛变量；m为二次曲线逼近技术的参数，可以选择m=4以获得较高的精度。注意，约束条件式(19)可以被一组类似于式(27)中的二阶锥不等式所代替。

2.5 SOCP变换和基于SCA的算法

(28)

s.t.(1)～(4),(13)～(15),(19)～(21),(24),(26),(27)

(29)

(30)

0≤oijk≤1,0≤ai≤1，

(31)

式(31)目标是放松变量o和a。当A是一个较大的整数值时，该变量由式(29)和式(30)执行。

本文定义Γ(n)为在第n次迭代时得到的客观值，当|Γ(n)-Γ(n+1)|≤10-3时，建立了算法1的收敛准则。

算法11:Set n:=0;2:Initialize starting points for β(n) and θ(n);3:repeat;4:Solve the SOCP problem (16) in order to obtain;P∗,θ∗,s∗,o∗,a∗,f∗,b∗,r∗,α∗,β∗,k∗,δo∗,δa∗;5:Set n=n+1;6:Update β(n)=β(n) and θ(n)=θ∗;7:until Convergence of the object function (28).

3 仿真与分析

对本文提出的卸载算法进行详细的评估。仿真场景设置为UAV-MEC物联网系统下的物联网设备(地面终端设备)数据处理场景，如图1所示。在仿真过程中，假定物联网系统中所有的设备都随机分布在以无人机起始点为中心的半径为10 000d0的圆形覆盖范围(参考距离d0=1 m)。无人机以固定高度H=50 m保持飞行状态。参考距离d0=1 m，信道功率增益设置为g0=-50 dB，对于物联网系统中的第i个地面终端设备，其所需计算任务的输入数据大小di，遵循均匀分布[30,70]kb。设置Ci=[150,250]Hz，机载云平台的计算能力Fj=1 200 MHz，系统中第i个地面终端的计算能力为Cmax=300 MHz。噪声功率谱密度N0=-174 dBm/Hz。另外，第i个地面终端设备的传输功率被设定为Pij=30 dBm，假设系统无线电带宽为B=40 MHz。根据机载云平台计算能力，实验场景由M=3架安装Cloudlet的无人机和N=20个地面终端设备组成。具体仿真参数如表1所示。

表1 仿真参数

为了验证所提算法的合理性，对所提出的SCA-SOCP算法进行性能评估，如图2所示。

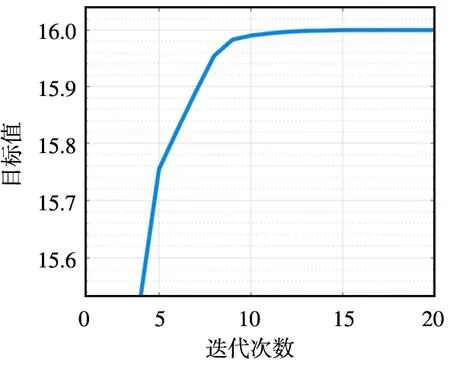
(a) 算法的收敛性评估

(b) 不同可靠性需求的终端对卸载率影响

首先，对算法收敛性进行评估，如图2(a)所示，在有限次迭代之后，目标值收敛到稳定值。而针对不同等级的移动终端，分析了Cloudlet可靠性对卸载率的影响，如图2(b)所示。其中，Rel1，Rel2，Rel3分别表示了Cloudlet的可靠性。当终端可靠性要求较低时，具有较低可靠性的Cloudlet对任务的卸载率影响低，因为子任务需要的冗余小，且不占用大量资源。当终端对Cloudlet可靠性要求较高时，子任务需要更多的冗余，从而消耗更多的资源，限制了移动终端数量。此外，当终端的可靠性要求较高时，算法1的复杂度增加，需要更多次的迭代才能收敛。因此，需要权衡无人机Cloudlet可靠性和资源利用率。图2(c)表示Cloudlet的计算资源和不同等级终端的时延对卸载率的影响。由于当Cloudlet计算资源增加，卸载率就会提高，因此计算时延将会降低，从而满足任务时延要求。然而，当任务具有严格的时延限制时，卸载率会下降，此时与可用的Cloudlet计算能力无关。因为子任务需要消耗更多的资源来满足任务时延要求，限制其他任务的可用资源，从而降低了任务卸载率。

在对所提出的SCA-SOCP算法进行性能评估后，还分析了不同时延要求和无人机云平台的可靠性对卸载率的影响，如图3所示。

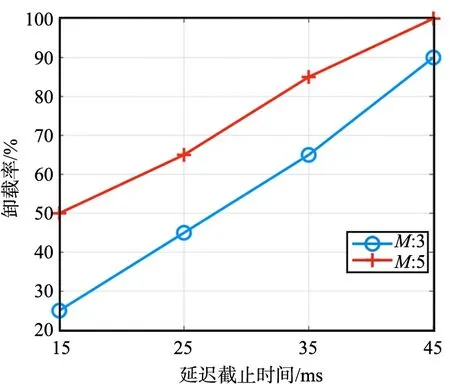
(a) 不同延迟需求下卸载率变化

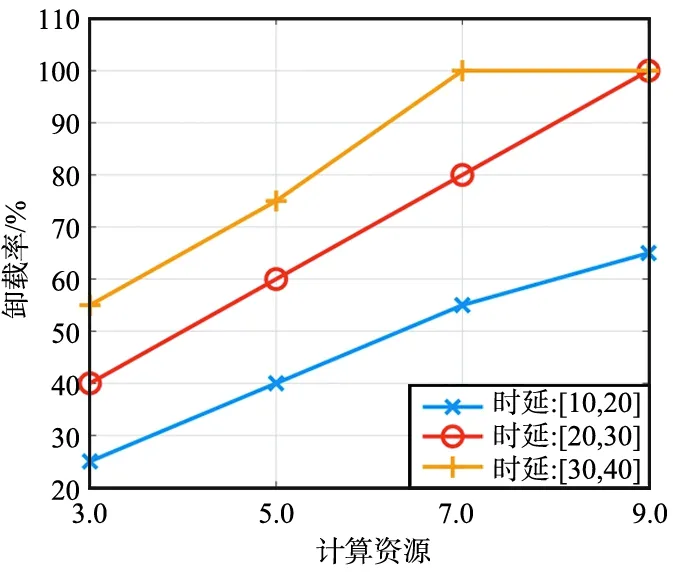
(b) 不同计算资源下卸载率变化图3 不同时延要求和不同计算资源对卸载率的影响Fig.3 Influence of different delay requirements and computing resources on unloading rate

由图3可以看出，当时延要求增加时，可以获得更高的卸载率；当可用无人机数量增加时，可以获得更多的计算资源。随着无人机的可靠性增加，当终端卸载任务量增加时，在时延和可靠性之间存在一种折衷，即增加任务分区可以降低由并行计算所导致的任务延迟，但可靠性会降低。

本文将算法1与无线带宽在终端间平均分配的SCA-EB算法，以及未优化无人机位置的SCA-FP算法进行比较，同时研究任务大小增加的影响，结果如图4所示。可以看出，算法1在卸载率方面优于其他方法，证明优化无人机的位置可以产生积极的影响，因为通过增加上行速率可以降低传输延迟。此外，对于计算量大的任务，需要消耗更多的资源来满足时延要求，由于通信和计算资源在其他2种方法中没有进行优化，因此相对于本文提出的算法卸载率更低。

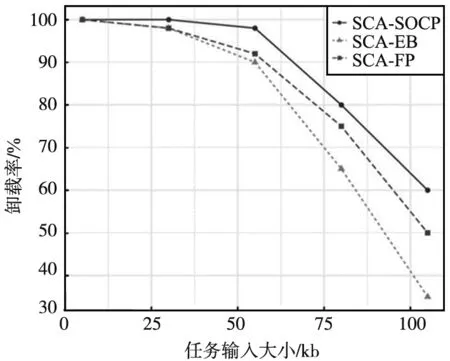
图4 任务大小对卸载率影响Fig.4 Influence of task size on unloading rate

4 结论

本文研究了基于机载云平台的可靠性感知MEC卸载问题，根据所需的延迟和可靠性，最大化所允许的任务数量。提出了一种基于连续凸近似方法的低复杂度迭代算法。该算法优化了无人机的位置、终端的任务划分、终端设备与无人机的关联以及考虑计算冗余的资源分配。仿真实验表明，与典型卸载策略算法相比，提出的SCA-SOCP卸载算法可靠性更高，可有效减少任务计算时延，节约成本，验证了该算法的有效性，未来工作会综合考虑系统能耗、延迟以及可靠性，来研究机载云平台卸载策略。