基于RFT的随机调频周期LFMCW雷达微弱目标检测

祁萍萍，李 琦，韩壮志

(1.河北工业大学 电子信息工程学院，天津 300401；2.陆军工程大学石家庄校区 电子与光学工程系，河北 石家庄 050003)

0 引言

线性调频连续波(Linear Frequency Modulated Continuous Wave,LFMCW)是频率作周期性变化的一种信号，收发信号产生的时间差可以通过频率的差异显现出来[1]，该波形没有距离盲区且具有较高的距离分辨率[2]目标信号的时延远小于雷达信号时宽。LFMCW雷达与脉冲雷达获得目标信息的方式不同,是对发射信号与回波信号的差拍信号进行处理，目标的速度和距离信息隐藏在差拍信号的参数中[3]。对于信噪比较低的微弱目标，需要对差拍信号进行长时间积累才能检测到目标。而当目标运动时，目标在相参积累时间(Coherent Integration Time，CIT)内会移动一段距离，因此产生距离走动现象，从而不能正确地估计目标距离，需要采取措施消除长时间积累带来的跨距离单元走动问题。目前，已经提出了很多方法解决距离走动问题，文献[4]提出对差拍信号进行Keystone变换，不需要已知目标的速度就可以对距离走动进行补偿，然而，这种方法不能解决多普勒模糊问题。文献[5]提出Radon-Fourier变换(RFT),应用于脉冲多普勒雷达中，通过对回波信号的距离-速度进行联合搜索来估计目标的距离和速度信息。本文采用基于RFT的相参积累算法，对发射信号与回波信号混频产生的差拍信号在速度维和距离维进行联合搜索,在速度和距离二维平面积累能量，从而估计目标的速度和距离信息。

RFT本质上是一种广义多普勒滤波器组,不受目标径向速度、距离走动和多普勒频率模糊的影响[6]。但在实际应用中，受离散采样、有限积累周期数和有限距离分辨率的影响，RFT算法会产生盲速旁瓣(Blind Speed Side Lobe，BSSL)[7]，BSSL会使雷达虚警率提升，从而检测不到小目标[8]。为了抑制BSSL，文献[9]通过在慢时间维增加对称窗来抑制BSSL，但该方法对BSSL的抑制效果较差。

综上所述，本文在二维FFT的基础上，通过RFT对差拍信号在速度维和距离维进行联合搜索来获取目标的速度和距离信息。针对固定调频周期下RFT会产生BSSL的问题，通过在固定调频周期上增加一个随机抖动量来抑制BSSL，首先导出BSSL的抑制效果与添加抖动量的大小的关系，然后分析添加随机抖动量的大小对BSSL抑制效果的影响，得出BSSL的抑制效果随着抖动量的增大而改善，当抖动到最大幅度时，BSSL得到有效抑制，最后通过仿真实验证明该方法的有效性。

1 信号分析

1.1 差拍信号分析

本文采用LFMCW锯齿波作为雷达发射信号。LFMCW 雷达锯齿波差拍信号产生原理[10]如图1所示。其中，f0为载频，B为信号带宽，T为调频周期。

图1 LFMCW 雷达锯齿波差拍信号产生原理Fig.1 Schematic diagram of sawtooth wave beat signal generation of LFMCW Radar

第m+1个调频周期的发射信号形式为：

(t∈[mT,(m+1)T])，

(1)

式中，k=B/T为线性调频率；m为调频周期数；A1为幅度。其时宽带宽积D=BT，一般情况D≪1，所以可以得到较高的距离分辨率。

假定目标匀速运动，则目标回波信号相对于发射信号的延迟为：

(2)

则第m+1个调频周期回波信号表示为 ：

(3)

式中，A0为回波信号增益。

为了使t的取值范围不受调频周期数m的影响，用t+mT代替式(1)和式(3)中的t，通过发射信号Sam与回波信号Sbm混频，得到差拍信号形式为：

(4)

式中，A=A1A0。

把式(2)代入式(4)，并忽略和c2有关项，可得：

(5)

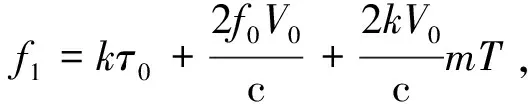
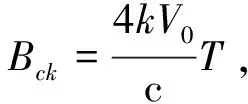
因此差拍信号可以近似为一个固定频率的信号,如下：

(6)

对差拍信号在距离方向做FFT处理，得到第m+1个调频周期的频域信号为：

(7)

由式(7)可以看出，差拍信号经过距离方向FFT之后的中心频率为：

(8)

1.2 差拍信号的二维FFT分析

由式(7)可以看出，由M个周期的差拍信号频谱峰值组成的慢时间维信号可以表示为：

(9)

线性调频锯齿波二维FFT的处理过程为：

① 对每个调频周期采样后的差拍信号做一维N点FFT运算，假设调频周期数为M，则需要进行M次N点FFT运算。

② 对M个调频周期的N点FFT的结果每一列进行二维的M点FFT运算，这个过程称为相参积累，得到一个M行N列的矩阵，其中行对应的是中心频率，即距离维，列对应的是多普勒频率，即速度维。

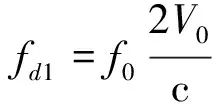
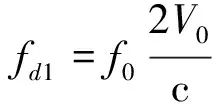
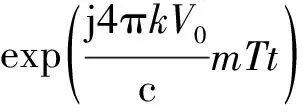
2 RFT算法的实现

2.1 RFT的原理

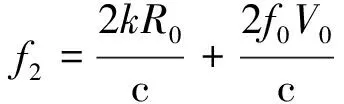
(10)

式中，tm=mT表示第m个调频周期的慢时间。

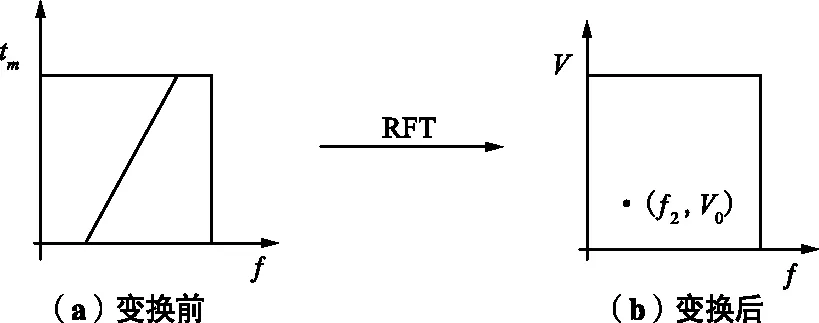
图2 RFT 变换示意Fig.2 Schematic diagram of RFT transformation

式(10)仅对参数为(f2,V0)的直线进行积累，实际处理中需要按照一定的步长对目标所有可能的参数进行搜索，所以式(10)可以写为：

(11)

式中,fi=fmin+iΔf,i=1,2,…,Nr,fi∈[fmin,fmax],fmin和fmax是搜索的最小和最大中心频率，它由雷达探测范围的目标飞行区域和飞行速度决定；Vq=-Vmax+qΔv,q=1,2,…,Nv,Vq∈[-Vmax,Vmax],Vmax为速度检测范围内的最大值；Δf为搜索的中心频率单元大小；Nr为搜索的中心频率单元数；Δv为搜索的速度单元大小；Nv为搜索的速度单元数。当(fi,Vq)=(f2,V0)，即搜索参数等于目标的真实参数时，式(11)出现峰值。

RFT无需对目标距离走动进行校正,通过对目标的初始距离和速度进行搜索来获取目标的信息[15]。RFT的核心思想是多维度联合搜索，通过遍历所有搜索参数对以完成目标的相参积累[16]。对于每一组的搜索参数，根据目标运动参数与跨距离单元数的耦合关系，通过循环移位对每一个调频周期内采样点完成包络对齐，把对齐后的信号抽取出来，然后通过多普勒滤波器组完成目标的能量积累，最后，将目标能量投影到运动参数域。

2.2 RFT的计算方法

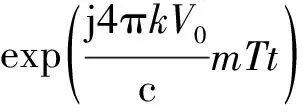
(12)

对式(12)在距离方向进行FFT：

(13)

由式(13)可以看出，当Vq=V0时，中心频率不再随着调频周期数m的变化而变化，为一固定值，此时对式(13)进行相参积累，可积累出最大值。因为差拍信号慢时间维的频率被补偿为零，所以，可以通过对Scm′(f,m)的方位向进行叠加，完成相参积累[17]，如下：

(14)

式中，M为总的调频周期数。

2.3 随机调频周期RFT原理

利用RFT检测目标时，可能会有BSSL的产生。为了解决RFT的盲速问题，本文通过给固定调频周期添加一个随机抖动量来抑制BSSL。对于固定调频周期雷达，tm=mT表示第m个调频周期的慢时间。当添加随机抖动量后，T介于第m和第m+1个调频周期的表示为：

Tm,m+1=(1+σm,m+1)T，

(15)

式中，{σ1,2,σ2,3,…,σM-1,M}是随机抖动量。由上式可以看出，固定调频周期可以看作是上述模型的特例，条件是σ1,2=σ2,3=…=σM-1,M=0。

给固定的调频周期加上了随机抖动量，使每个调频周期随机变化，其对应的慢时间如下：

(16)

式中，σm在[-a,a]服从均匀分布，且0≤a≤0.5。假设第 1 个调频周期的采样时刻为零时刻，那么tm1就是前m个调频周期的和。

对式(11)在(f,V)空间进行离散化，可得：

exp(j4π(V-V0)mT/λ)。

(17)

由式(17)可以看出，当f=f2时，V=V0可获得理想增益AM。

事实上，式(17)中的相位起伏不仅在V0处可以被补偿,在V(p)=V0+pVb,p=±1,±2,±3,…都可以被补偿掉。把V(p)代入式(17)可得：

exp(j4π(V(p)-V0)mT/λ)=

(18)

所以，在f=f2，p≠0的情况下，RFT会在(f2,V(p))产生较大的积累峰值，即为BSSL。

采用随机调频周期RFT在(f2,V(p))的能量积累如下：

exp(j4π(V(p)-V0)(mT+σmT)/λ)=

(19)

一般情况下σmT≪ρr，可认为随机调频周期对包络的选取没有影响，所以上式可以简化为：

(20)

对式(20)求均值得：

(21)

由式(21)可见,BSSL被乘上了衰减函数，当a=0.5时上式可以转换为：

(22)

sinc(p)的取值如图3所示。因为p的绝对值为大于等于1的整数，可以看出此时sinc(p)几乎为零，各个BSSL幅度基本被衰减为零，当a<0.5时，会使2ap出现小于1的可能，使衰减函数sinc(2ap)不接近于零，导致在目标真实速度附近的盲速不能被有效抑制掉。所以a=0.5的抑制效果最明显，a越小抑制效果越差。

图3 sinc(p)函数图形Fig.3 sinc(p) function graph

为了进一步量化BSSL的抑制效果，可以采用主瓣的峰值与BSSL均值的峰值来衡量，峰值旁瓣比(PSLR)为：

(23)

从式(23)可以看出，PSLR随着抖动量a和调频周期数M的增大而增大，因此可以通过增大抖动量a和增加调频周期数来提高BSSL的抑制性能。

3 实验与分析

为了验证理论分析的正确性，对上述分析进行仿真实验。假设目标匀速运动，载频f0=24 GHz，信号带宽B=500 MHz，平均调频周期T=10 μs，距离维采样点数为512，目标初始速度V0=180 m/s，目标初始距离R0=100 m。

3.1 基于固定调频周期RFT相参积累结果

二维FFT的积累结果如图4所示。

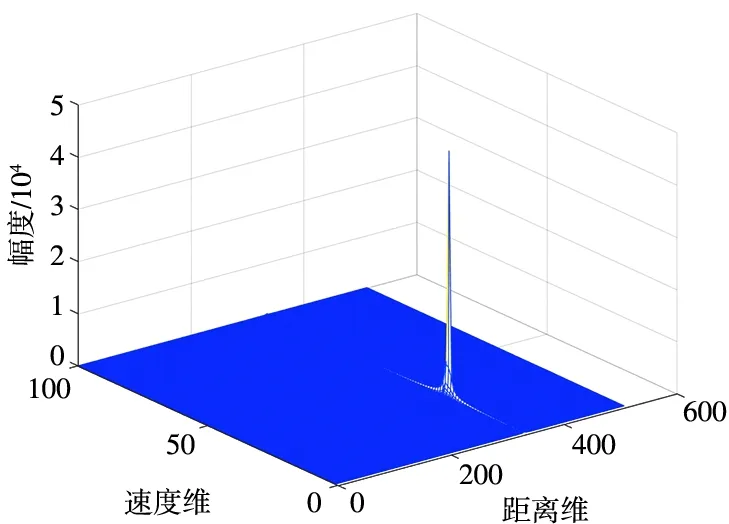
(a) M=100时二维FFT的积累结果

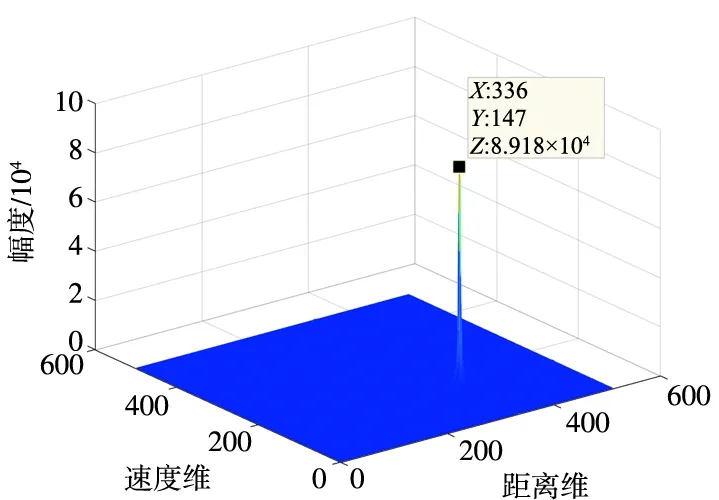
(b) M=500时二维FFT的积累结果图4 二维FFT的积累结果Fig.4 Accumulation results of two-dimensional FFT

当调频周期数M=100时，在调频周期固定条件下，采用二维FFT对差拍信号进行处理，此时距离分辨率ΔR=0.3 m，在一个CIT内，目标的距离走动量为Δr=V0MT,通过所设定的参数计算可得Δr=0.18 m，目标没有跨距离单元走动，目标能量聚集在一个距离单元内，但存在速度模糊，如图4(a)所示。当调频周期M=500时，此时Δr=0.9 m，通过计算可知，目标走动了3个距离单元，此时对差拍信号进行二维FFT，能量散布在多个距离单元内，如图4(b)所示。对目标进行二维FFT，要求目标回波在一个距离单元内，明显二维FFT已经不适用于存在距离走动的目标。

当调频周期M=500时，采用RFT 处理时，RFT的积累结果如图 5所示。可以看出，目标的能量被有效积累，差拍信号的幅度由原来的8.918×104变成了1.249×105，除了目标能量积累的峰值外，积累结果还存在BSSL。

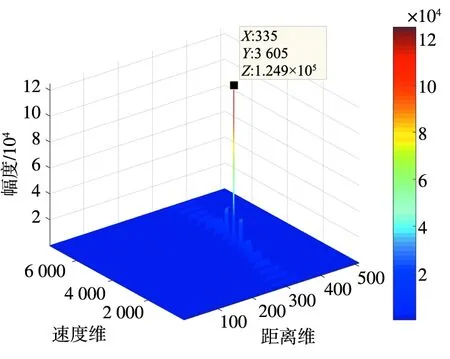
图5 RFT的积累结果Fig.5 Accumulation results of RFT

3.2 基于随机调频周期RFT相参积累结果

在上述条件的基础上，通过给固定调频周期添加随机抖动量来抑制BSSL，BSSL的抑制效果与添加的随机抖动量的大小有关，分析得出：

① 当a=0.3时进行RFT处理，BSSL得到有效抑制，但仍有部分BSSL没有被抑制，如图 6(a)所示；

② 当a=0.5时进行RFT处理，BSSL基本被抑制掉，如图6(b)所示;

③ 图6(c)给出了第一BSSL的PSLR随着抖动量a变化的曲线图，可以看出随着抖动量a的增大，PSLR逐渐增大。

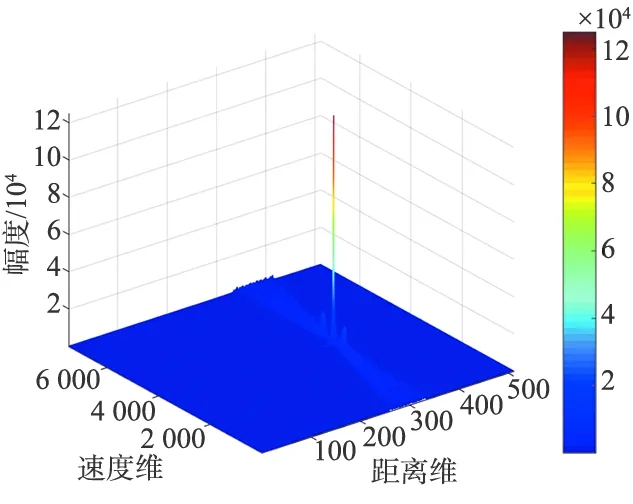
(a) a=0.3时RFT积累结果

(b) a=0.5时RFT积累结果

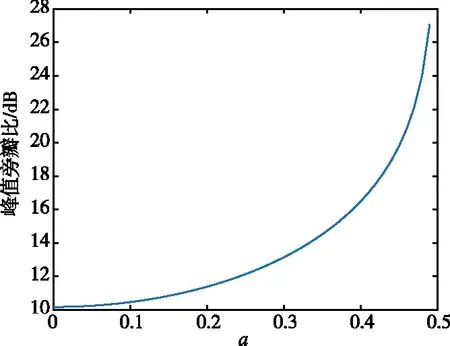
(c) p=1时PSLR随抖动量a的变化曲线

上述仿真实验有效证明BSSL的抑制效果与抖动量的大小有关，a越接近0.5，BSSL抑制效果越好，当a=0.5时，BSSL基本被抑制掉。

3.3 基于随机调频周期RFT对微弱目标的检测性能

在上述的基础上加入高斯白噪声，且信噪比为-30 dB，调频周期数M=1 000,设定a=0.5，其他条件与上面相同，此时目标走动了6个距离单元，积累结果如图7所示。

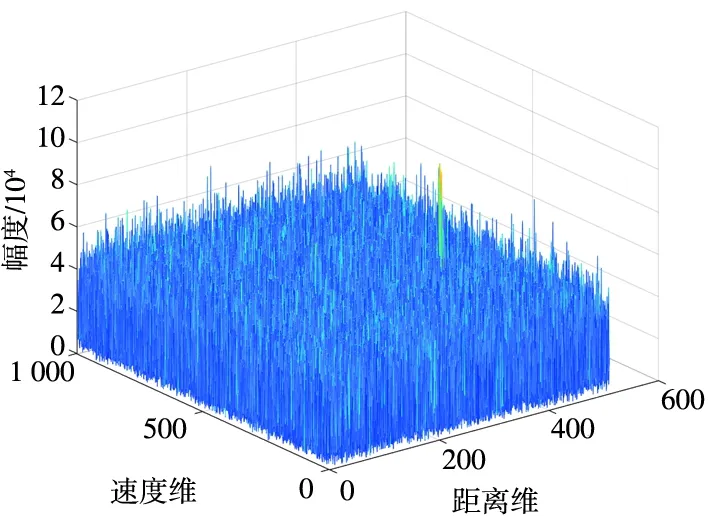
(a) 二维FFT的积累结果

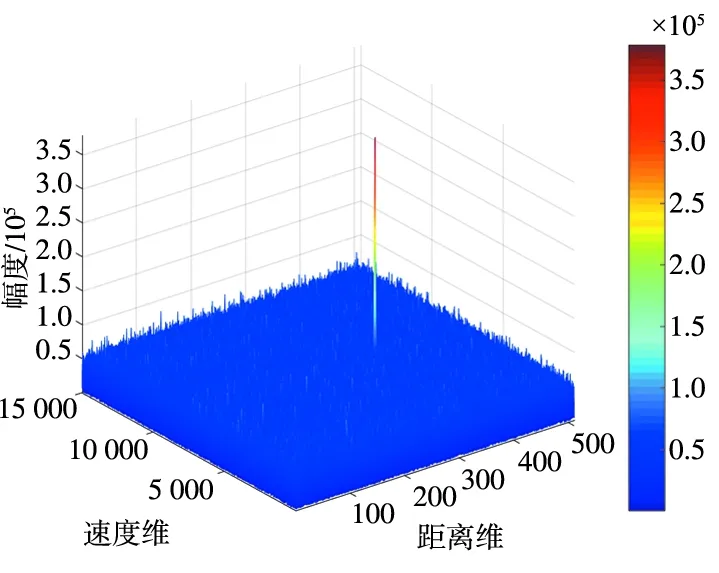
(b) RFT积累结果图7 加噪声后的二维FFT和RFT的积累结果Fig.7 Accumulation results of two-dimensional FFT and RFT after adding noise

图 7(a)中二维FFT处理后，目标与噪声混在一起，通过仿真实验，仿真输出的信噪比I0= 15.860 9 dB；而采用随机调频周期RFT 处理，目标信号被有效积累，BSSL被淹没在噪声中，如图 7(b)所示。仿真输出信噪比I1 =26.972 1 dB。可见，基于随机调频周期RFT相比于传统的二维FFT，有效提高了信噪比，可以实现对信噪比较低的微弱目标的检测。

为进一步验证该方法对微弱目标的检测性能，在虚警概率Pf=10-6条件下，本文提出的BSSL抑制方法与加对称窗BSSL 抑制方法的目标检测性能的蒙特卡罗仿真结果如图8所示。可以看出，在相同信噪比下本文方法的检测概率比加对称窗的检测概率要高，因此，该算法提高了对微弱目标的检测性能。

图8 目标检测性能曲线Fig.8 Target detection performance curve

4 结束语

针对LFMCW雷达对微弱目标检测过程中长时间积累导致的跨距离单元走动问题，本文利用RFT对差拍信号在速度维和距离维进行联合搜索，从而得出目标的速度和距离信息，但是在固定调频周期下RFT可能会产生BSSL，使雷达虚警概率增加而影响 RFT 的检测性能，为此，针对RFT存在BSSL的问题，本文通过给固定调频周期上加上一个随机抖动量来消除BSSL，推导了BSSL的幅度与添加抖动量大小的关系式，关系式表明BSSL因乘上了一个衰减因子而被抑制掉，仿真实验证明了本文方法可以对具有距离走动的微弱目标进行有效的检测并且有效地抑制了BSSL问题。