基于动态规划模型的水资源优化配置——以泰来灌区为例

徐淑琴，徐恩典，马圣洁

（东北农业大学水利与土木工程学院，哈尔滨 150030）

近年来，我国针对大型灌区普遍存在的设计标准低、配套程度差、老化损坏严重、用水效率低、管理体制不顺以及经营体制不活等问题进行系统整改，以促进我国农业发展、农村经济繁荣和农民收入提高。特别是我国北方灌区，存在沟渠冲淤、骨干渠道衬砌不足等问题，水资源严重浪费，影响灌区总体效益发挥。为保证灌区正常运行，发挥自然优势，提高粮食产量和质量，近年来对大型灌区骨干工程实施配套和节水改造政策，单位面积净效益及单位水量经济效益问题仍亟待解决。

针对此问题国内外学者开展一系列研究，张帆等以甘肃省黑河中游17 个灌区间水资源优化配置为例，以经济效益、社会效益、生态效益为目标函数构建多目标优化模型，分别使用传统方法与复合多目标方法进行求解，所获优化配置方案可将灌溉水利用系数提高5.42%～7.57%，验证复合多目标方法所获得的优化方案更能体现决策者对研究区域种植业发展与灌区水资源配置的多元要求[1]，但单目标模型在其对应目标上表现更优。杜丽娟等采用GWAS 模型，通过划分水资源配置子单元和设置调蓄节点，采用公平性最优和供水缺水率最小为目标函数，总量控制、供水能力、分质供水等为约束条件，将水资源优化配置问题模拟为生物进化问题，采用基于精英策略的非支配遗传改进算法求解，建立适用于淠史杭灌区水资源优化配置模型[2]，但其研究分析频率对象较少，难以真实反映情况，出现偏差几率较大。Cheng等考虑目标函数各变量在同一阶段独立且约束条件变量逐级递增的特殊性，提出一种一维动态规划递推优化方法，得到初始解离散差分动态规划（DDDP）算法，解决多维动态规划模型中每个阶段包含3 个状态变量和3 个决策变量的问题[3]。李茉等针对灌溉水资源优化配置中存在的非线性和不确定性等特点，建立区间线性分式规划（ILFP）模型以获得最大灌溉水生产力和考虑下层农民利益的区间二次规划（IQP）模型以获得最大产量，并在此基础上构建LFQBP 模型，促进灌区可持续发展[4]。谭倩等针对农业水资源多目标规划中存在的权重不确定性难题，建立基于鲁棒优化方法的农业水资源多目标优化配置模型方法（MRPWU），达到节省灌溉用水，提高生态效益的目的[5]。综上表明，在已完成配套和节水改造的大型灌区内建立合理的优化灌溉制度方案是提升灌区整体经济效益的有效方法。本文针对此问题建立动态规划模型研究灌区单位面积及单位水量净效益，以获取最大经济效益。

1 研究区域概况

1.1 灌区概况

泰来灌区位于泰来农场境内，灌区北以大排干末端为界，南至农场场界，西部以第四作业区田间道为界，东部以嫩江堤防为界。灌区南北长10.5 km，东西宽8.0 km，水田总控制面积3.75×107m2，设计灌溉面积3.33×107m2。灌区范围内地面比降为1∶300～1∶3 000，地面高程海拔136～133 m。多年平均气温4.2 ℃，最冷1月份平均气温-17.6 ℃；极端最低气温-35.2 ℃。最热7月份，平均气温23.4 ℃，极端最高气温41.6 ℃。无霜期约130 d，多年平均降水量369 mm，6～8月份降水量占年降水量73.6%，多年平均蒸发量1 798.2 mm，年平均≥10 ℃有效积温2 500～2 700 ℃，年平均日照2 917.8 h，最大冻土深度1.95 m，本区属高温少雨地区，一般春季降雨少、风大，最高可达8～12级。

1.2 水资源概况

1.2.1 地表水资源概况

泰来农场位于嫩江右岸低平原区，灌区属嫩江流域。本区多年平均降雨量369 mm，6～8月份降水量占年降水量73.6%，多年平均径流深118.2 mm。

本区处于松嫩平原最为干旱的平原地区，当地地表径流极少，且年际变化较大，枯水年难以利用。季节性河流一棵树沟（大排干）在场区中部穿过，为主要排水沟，承泄区为嫩江。流经本地区的嫩江干流是灌区主要水源地，泰来灌区提水泵站位于嫩江江桥水文站下游49 km处，区间无较大支流汇入。

1.2.2 地下水资源概况

泰来灌区地处大兴安岭东南余坡和松嫩平原西部边缘过渡地带，地层岩性均为第四系松散堆积物。

根据《黑龙江省泰来县地下水资源调查评价报告》[6]和《黑龙江省齐齐哈尔地区环境水文地质调查研究报告》[7]得知，该区为地下水可广泛开采的富水区。表层孔隙潜水埋深为15～28 m，含水层厚度为15～90 m，含水层岩性为砂砾卵石、粉砂、细砂，单井出水量50～100 m3·h-1，单井影响半径为200～300 m。潜水化学类型以重碳酸钙、重碳酸钠为主，铁离子含量为5 mg·L-1，锰离子含量也较高，地下水矿化度0.16 g·L-1，pH 7.1～7.6，一般超过饮用水标准，但水质符合农业灌溉用水要求。

承压水层厚1.4～5.0 m，埋深36～48 m，日涌水量543 m3，水量丰富，水质优，pH 7.1～7.6，矿化度小于1.0 g·L-1，可用于生活饮用水。

该区域地下水补给模数为91 500 m3·a-1·km-2，开采模数为58 564 m3·a-1·km-2。

本区地下水资源为当地居民用水和旱田喷灌提供充足水源。

2 灌区水资源及水量供需平衡分析

2.1 灌区水资源分析

2.1.1 一棵树沟（大排干）水资源分析

一棵树沟汇水面积1.85×108m2，河道蛇曲发育，河长61 km，场区内长度为22.2 km，平均宽度30 m。河道虽常年有水，但流量较小，年平均流量0.09 m3·s-1，设计标准下不能作为灌溉水源，主要作用是区内排水。

2.1.2 嫩江水资源分析

嫩江为松花江北源，发源于大兴安岭伊勒呼里山中段南侧。嫩江干流由北向南流经嫩江、莫力达瓦、讷河、富裕、甘南、齐齐哈尔、龙江、泰来、杜尔伯特、大安、肇源等市、县、旗，在吉林省扶余县三岔河从左岸汇入松花江。嫩江干流全长为1 370 km，流域总面积为2.97×1011m2，泰来灌区渠首引水口处汇水面积为1.77×1011m2。

嫩江在泰来农场东部经过，流经农场段长12.5 km，河道自然比降0.35‰，河宽250～300 m，行洪最小宽度5.5 km，堤防长度10 km，防洪标准为20年一遇。嫩江流域径流主要集中在6～9月，约占全年径流量70%，春季4～5月份枯水期径流量约占全年15%，封冻期径流占全年10%。

根据《泰来农场水利工程初步设计》，嫩江中下游泰来农场段多年平均年径流量为2.10×1010m3，设计保证率情况下年径流量4.82×109m3。枯水流量25.8 m3·s-1。

2004年全国第二次水资源规划提出嫩江流域多年平均地表水资源量为2.94×1010m3，其中江桥以上为2.47×1010m3，比原规划增加6.66×109m3，江桥以上增加3.69×109m3，江桥以下增加2.97×109m3。

2.1.3 地表水资源开发利用现状

嫩江流域地表水资源开发利用包括黑龙江省、吉林省、内蒙古自治区用水。根据尼尔基水库初设统计，嫩江流域干流现状地表水总用水量约2.25×109m3。其中城市居民生活及工业用水量6.4×108m3，农牧业灌溉用水量1.23×109m3，湿地生态用水量3.75×108m3；嫩江流域七大支流现状总用水量约1.72×109m3，其中居民生活及工业用水量3×107m3；农牧业灌溉用水量1.58×109m3，湿地生态用水量1.12×108m3。干支流总用水量约3.97×109m3，占嫩江流域地表水资源量17.5%。江桥以上现状总用水量约2.41×109m3，占天然径流11.5%。

综上所述，本区水资源量丰富，为当地水田种植提供充足资源，灌区水源有保证。

2.1.4 灌区现状水量供需分析

2.1.4.1 灌区水田现状水量供需分析

灌区水源地嫩江水量充足，根据渠首泵站设计成果，现有嫩江渠首灌溉站设计流量4.86 m3·s-1。

灌区水田实灌面积3.33×107m2，现状灌溉水利用系数为0.65，保证率P=50%情况下水稻净灌溉定额8 220 m3·hm-1，灌溉毛定额12 645 m3·hm-1，年需水总量为4.215×107m3。如按灌水率1.158×105m3·s-1·hm-1，灌区最大需水流量5.94 m3·s-1，泵站设计流量4.86 m3·s-1，供水流量无法满足3.33×107m2水田同时引水灌溉要求。但因2号水库蓄水容积存蓄泵站引水，按照水泵每年供水时间122 d、每日工作时间20 h 计，泵站年供水能力4.268×107m3，满足灌区现状水田灌溉用水要求。

2.1.4.2 区内其他各业现状水量供需分析

根据对泰来县水资源开发利用状况的分析及建议得知[8]，该区域地下水补给模数为9.15×104m3·a-1·km-2，开采模数为5.8 564×104m3·a-1·km-2。区域1.02×108m2内年可开采量5.92×106m3。

区内其他用水包括生活用水、旱田喷滴灌用水和生态用水等，均取自地下水。生活用水主要为人畜用水，项目区内现状总人口0.28 万人，牲畜1 245 头，根据《黑龙江省地方标准〈用水定额〉（DB23/T727-2003）》[9]，农村生活人均用水定额0.080 m3·d-1，牲畜每头平均用水定额0.1 m3·d-1。每年人畜共消耗水量1.3×105m3。目前旱田灌溉面积6.67×106m2，按用水毛定额1 050 m3·hm-1计，年用水7×105m3。现状生态用水量为场区绿化地用水，体量较小，忽略不计。上述各业年用水总量为8.3×105m3。区内年可开采量远大于生活用水和旱田灌溉用水。

综上，灌区水利工程现状供水能力4.351×107m3，各业需水量4.298×107m3，水量富余5.3×105m3。

3 基于单位面积经济效益最大的动态规划模型及ASGA算法

3.1 模型设定

此动态规划模型实质是在保证灌水量前提下，在单位面积上获得最大经济效益。通过优化灌溉制度，实现灌区合理灌水。在稳步提升经济效益前提下，提高灌区水资源利用效率。以泰来灌区水稻灌溉制度为研究对象，以单位面积实际产量Ya与最高产量Ym比值最大为优化目标[10]。

3.2 单作物优化灌溉制度模型

3.2.1 目标函数

目标函数采用在供水不足条件下，水量和农作物实际产量连乘模型，目标函数为单位面积实际产量Ya与最高产量Ym的比值最大[11]，即

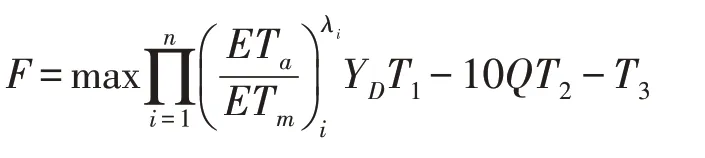
式中，ETa为实际蒸发量（mm）；ETm为最大蒸发蒸腾量（mm）；n为模型阶段总数；λi为缺水敏感指数,；YD为泰来灌区水稻多年平均最高产量，YD＝7 800 kg·hm-2；T1为泰来水稻市场平均价格，T1＝3.0 CNY·kg-1；Q为灌水总量（mm）；T2为水价，其中泰来灌区现状水价为0.1 CNY·m-3；T3为其他农业费用，包括种子、化肥、农药、人工、电费、物资等，平均8 000 CNY·hm-2。

3.2.2 阶段变量

根据作物生育过程，将作物全生育期划分为插秧返青期、分蘖期、拔节期、抽穗期、乳熟期。

3.2.3 状态变量

状态变量为各阶段初可用于分配的灌溉水量qi及初始田面蓄水深度hi。

3.2.4 系统方程

水量分配方程：

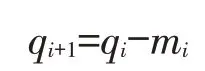
式中，qi、qi+1为第i及第i+1阶段初系统可用于分配水量（mm）；mi为第i阶段灌水量（mm）。

田间水量平衡方程：

式中，hi、hi+1为第i及第i+1 阶段初田面水层深度（mm）；Ci为第i阶段排水量（m3）；其余符号意义同前。

3.2.5 约束条件

3.2.5.1 决策约束

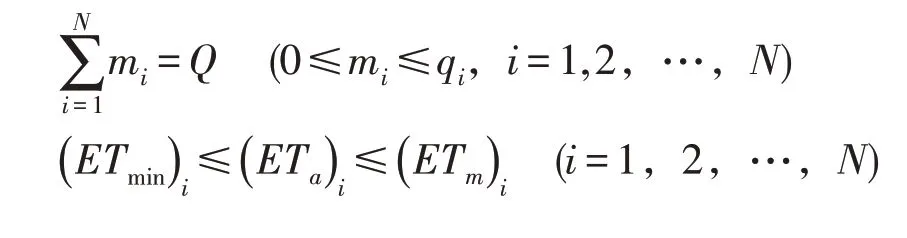
式中，Q为全生育期单位面积上可供分配水量（mm）；（ETm）i、（ETmin）i为第i阶段最大及最小蒸发蒸腾量（mm）。

3.2.5.2 田面水层hi约束

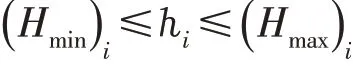
3.2.6 初始条件

3.2.6.1 初始田面水深

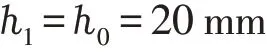
3.2.6.2 第一阶段可用于分配水量

第一阶段可用于分配水量为水稻全生育期可用于分配水量，即q1=Q1。

3.3 ASGA算法介绍

遗传算法作为一种有效全局搜索方法，其应用领域已渗透到多个学科中，如函数优化、组合优化、生产调度、自动控制、机器学习、图像处理、人工生命、遗传编程、机器学习、数据挖掘等[12-13]。传统GA（见图1）主要通过初始化种群，选择、交叉和变异算子寻求最优解以解决目标函数优化问题[14]，但由于其进化链条单一，有其自身缺点，如易产生早熟收敛、收敛速度慢、局部寻优能力较差等，且二进制编码遗传算法进行数值优化时，存在精度低缺点[15-16]。

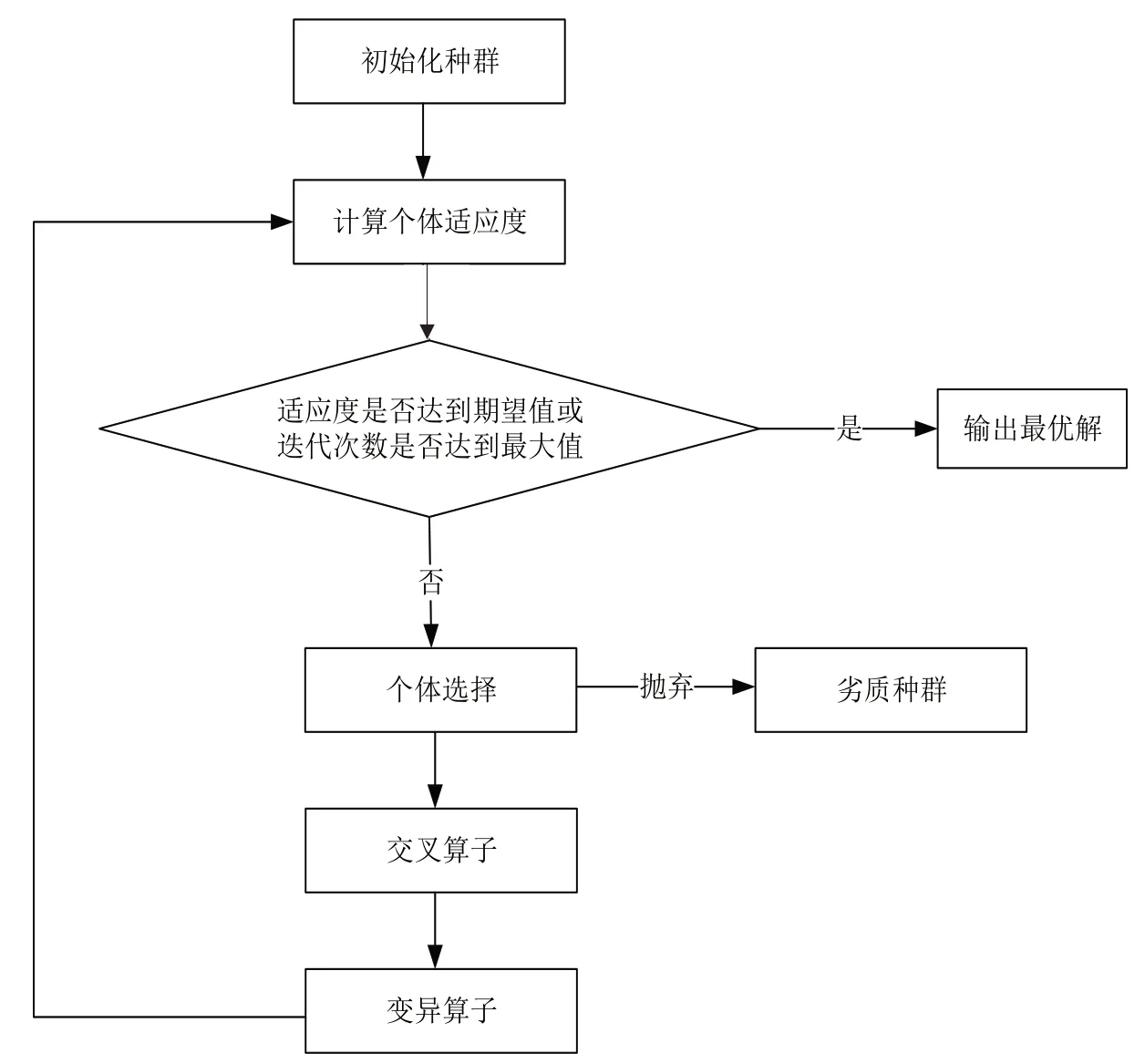
图1 传统GA流程Fig.1 Flow of traditional GA

ASGA（见图2）是在传统GA 中添加镜像算子（Mirror）、元组（Cell）操作和对比种群淘汰库：

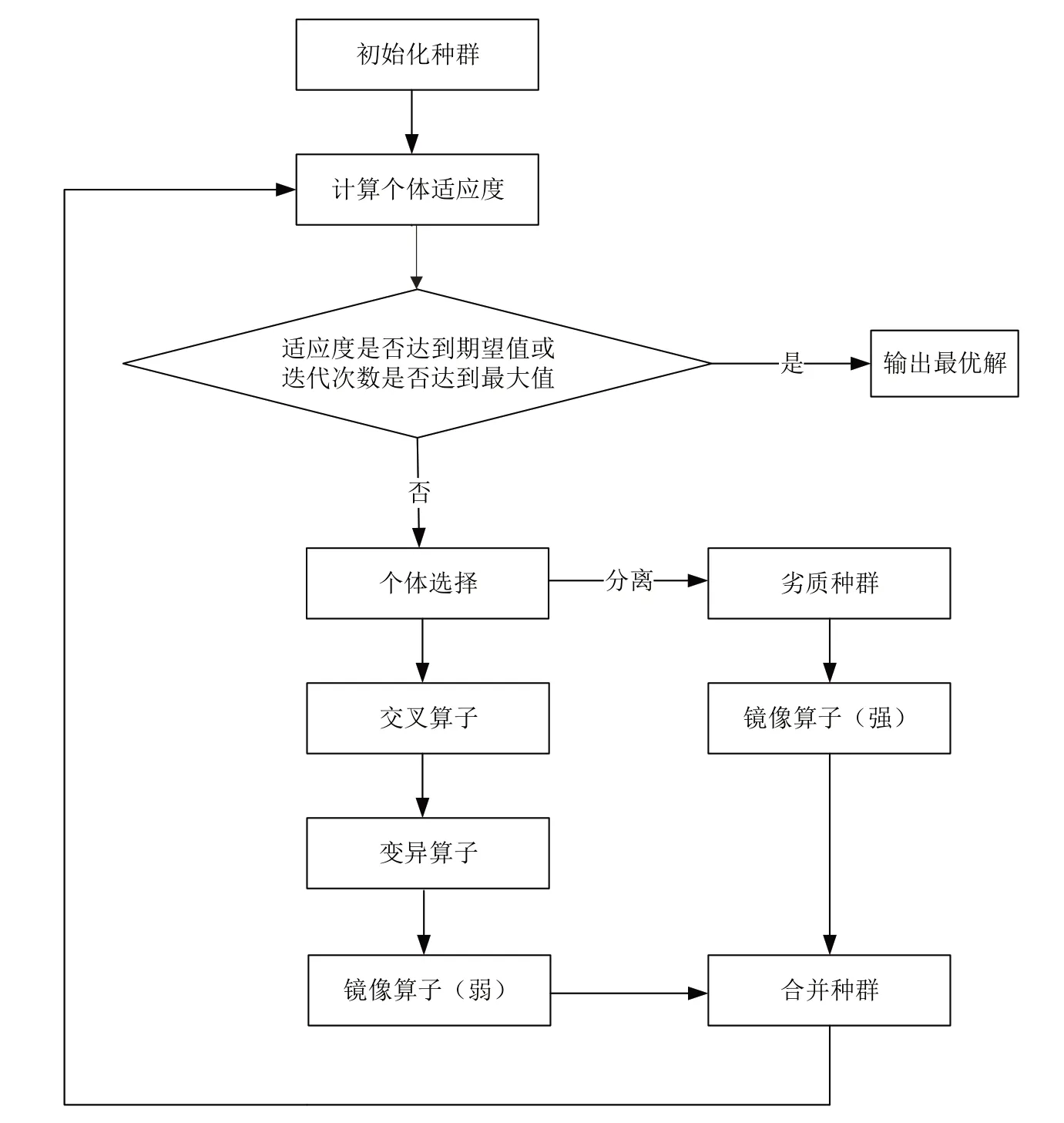
图2 ASGA流程Fig.2 ASGA flow

①镜像算子（Mirror）是一种对二进制编码染色体改变较强的算法，转码变化如下：

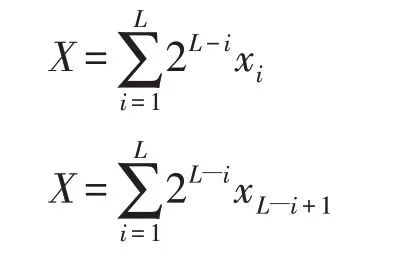
式中，X为十进制编码；L为二进制编码长度；x为二进制编码；i为左起二进制位数，以L=20，随机生成512组二进制编码种群进行镜像算子变化效果试验，结果如下：

由概率密度图（见图3）可知，染色体镜像前与镜像后各区域十进制数值取值概率分布相差较大，且二者呈现出反向极值现象，即在镜像算子优化前较多出现的十进制数值在镜像算子优化后出现次数骤减，因此可看出镜像算子是将种群内个体值向其相反性质方向改变，可使劣质个体在一定程度上向优质种群改变，以提升种群个体的最优概率。

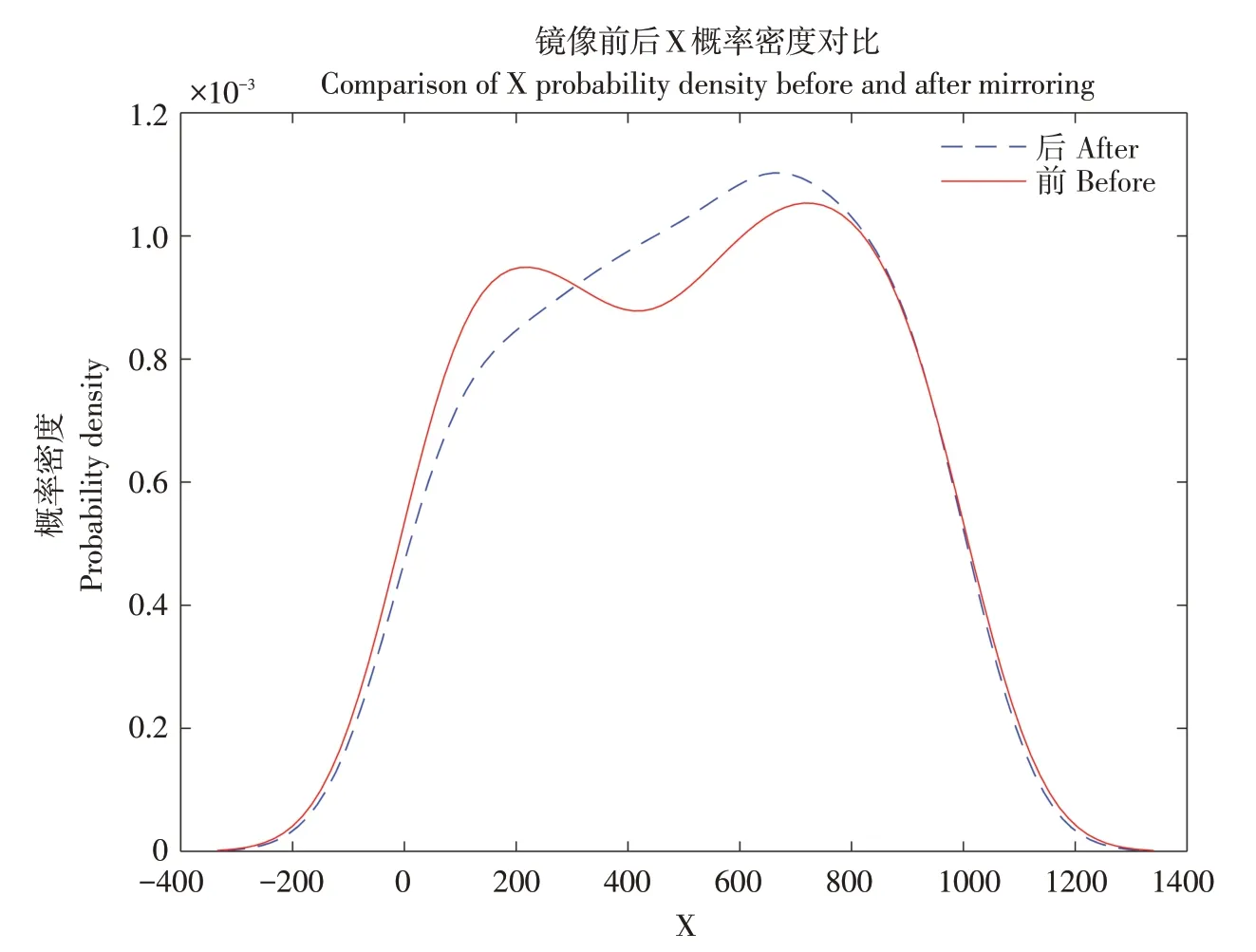
图3 镜像前后概率密度Fig.3 Probability density before and after mirroring

②元组操作是将二进制数据切块，种群分为n节（n为变量数），形成n个相对独立染色体模块并链接，形成染色体链（Chromosome-link），然后元组化地进行变异、交叉、镜像等操作，可节省代码量，条理清晰，提高程序运行速度，且各变量间变化维持相对独立性，在种群中可生成多种混合变量，以避免早熟问题[11]。

初始化种群染色体长度如下：

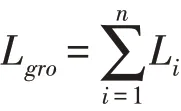
式中，Lgro为种群染色体总长度；Li为第i染色体模块长度，n为求解变量数。

③对比种群淘汰库。在优化过程中对比种群个体，淘汰较差个体，列入黑名单。淘汰库随优化过程不断更新，且淘汰库可用系数矩阵建立，占用空间小。

3.4 求解参数

参考充分灌溉作物生育时段划分方法，结合灌区多年耐冷优质水稻松粳系列品种叶龄模式判断生育进程，并参考2002年、1998年、2017年水稻试验结果，P=50%情况下水稻生育期时段参数见表1，P=75%情况下水稻生育期时段参数见表2，P=90%情况下水稻生育期时段参数见表3。

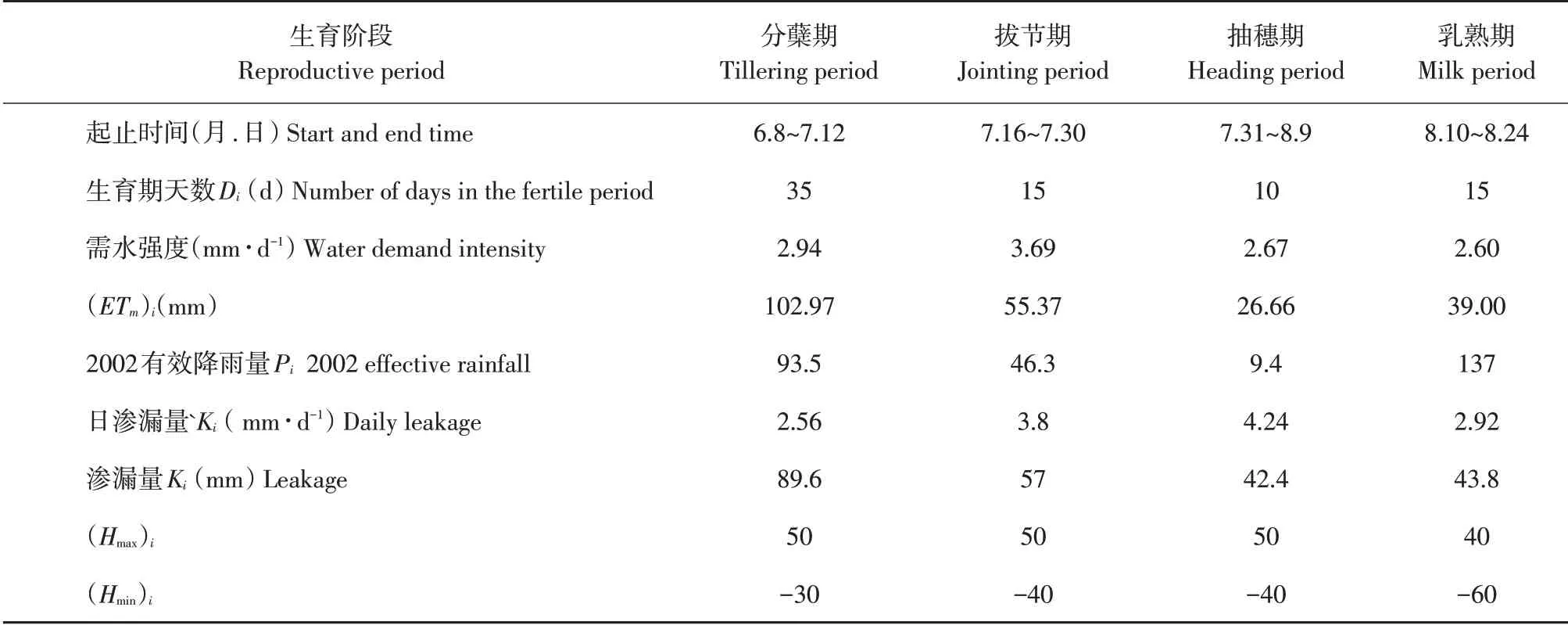
表1 泰来灌区水稻非充分灌溉下优化灌溉制度求解数据（P=50%）Table 1 Solution data of optimized irrigation schedule under insufficient rice irrigation in Tailai Irrigation District

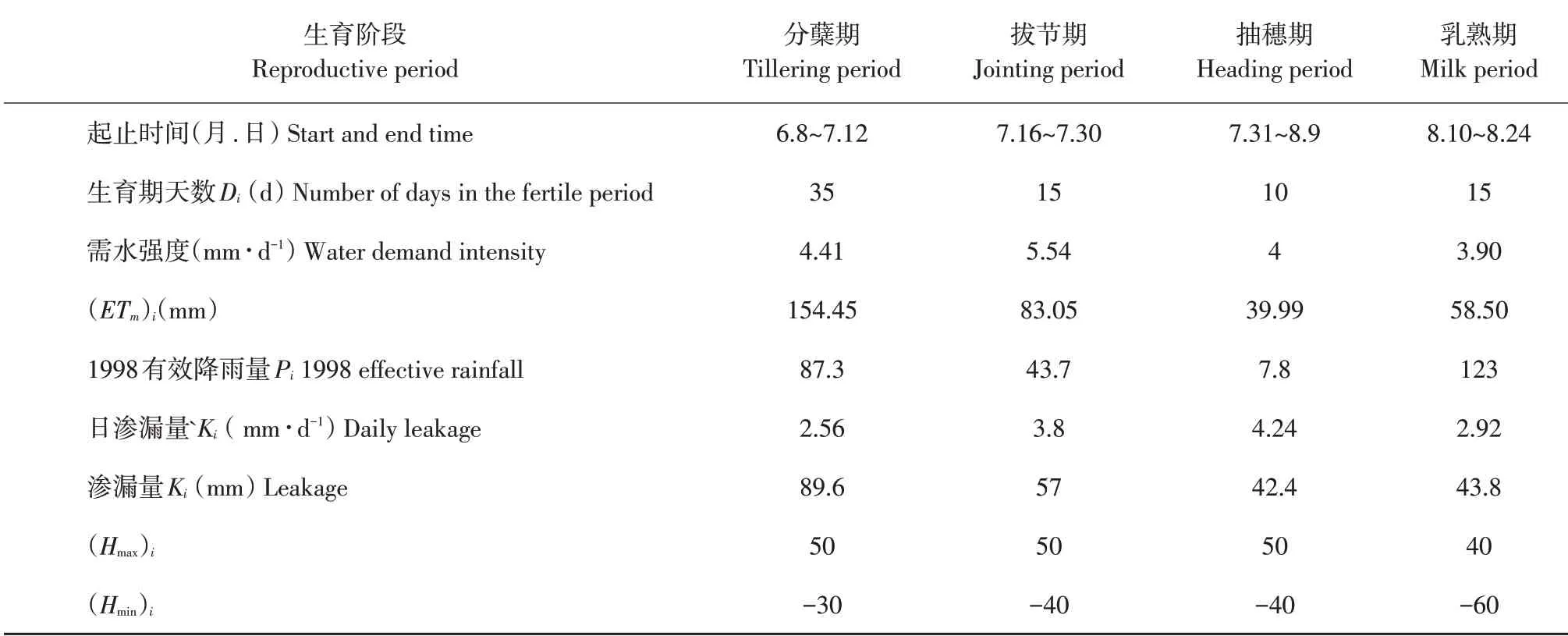
表2 泰来灌区水稻非充分灌溉下优化灌溉制度求解数据（P=75%）Table 2 Solution data of optimized irrigation schedule under insufficient rice irrigation in Tailai Irrigation District

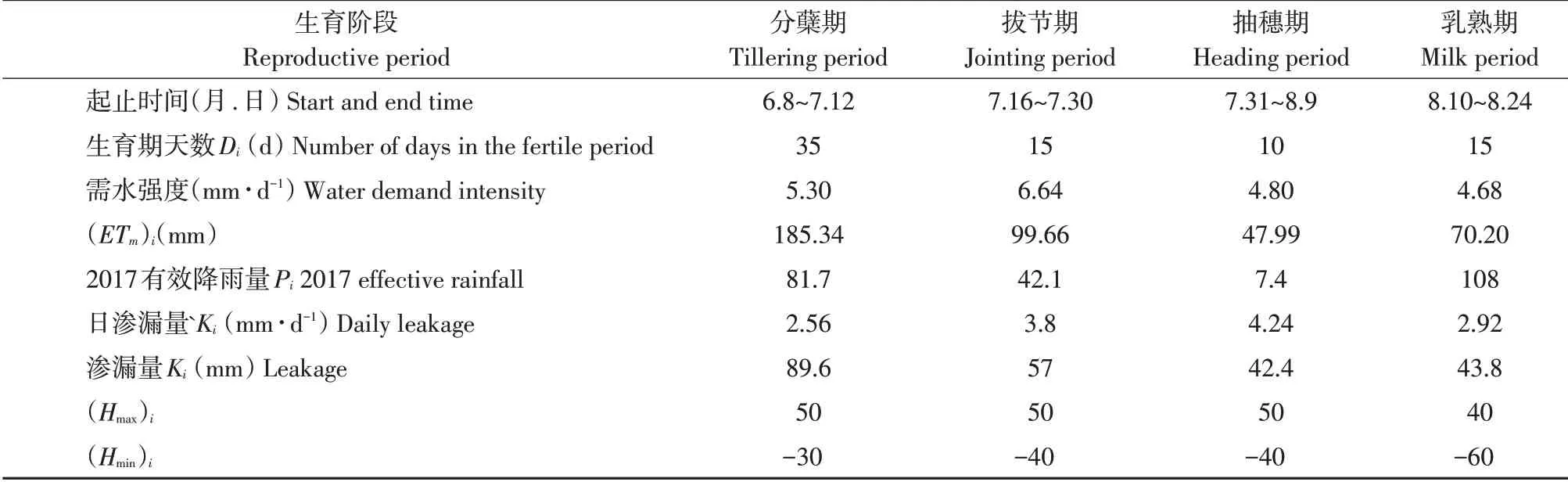
表3 泰来灌区水稻非充分灌溉下优化灌溉制度求解数据（P=90%）Table 3 Solution data of optimized irrigation schedule under insufficient rice irrigation in Tailai Irrigation District

4 求解结果及分析

对不同用水保证率（50%、75%、90%）水资源进行优化配置。水稻单作物优化应用ASGA优化原理，选定父代初始种群规模为N=400，交叉概率pc=0.80，变异概率pm=0.20，镜像概率pj=0.70，优秀个体数目选定为20 个，将原始数据输入，加速运行，得出不同供水量下目标函数最优值及优化结果见表4～7。保证率P=50%情况下单位面积净效益随灌溉定额变化见图4。

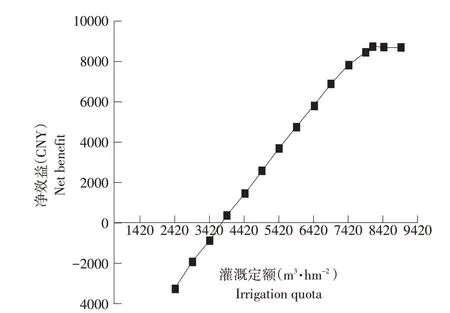
图4 单位面积（hm2）净效益随灌溉定额变化（P=50%）Fig.4 Changes in economic benefits per unit area(hm2)with irrigation volume

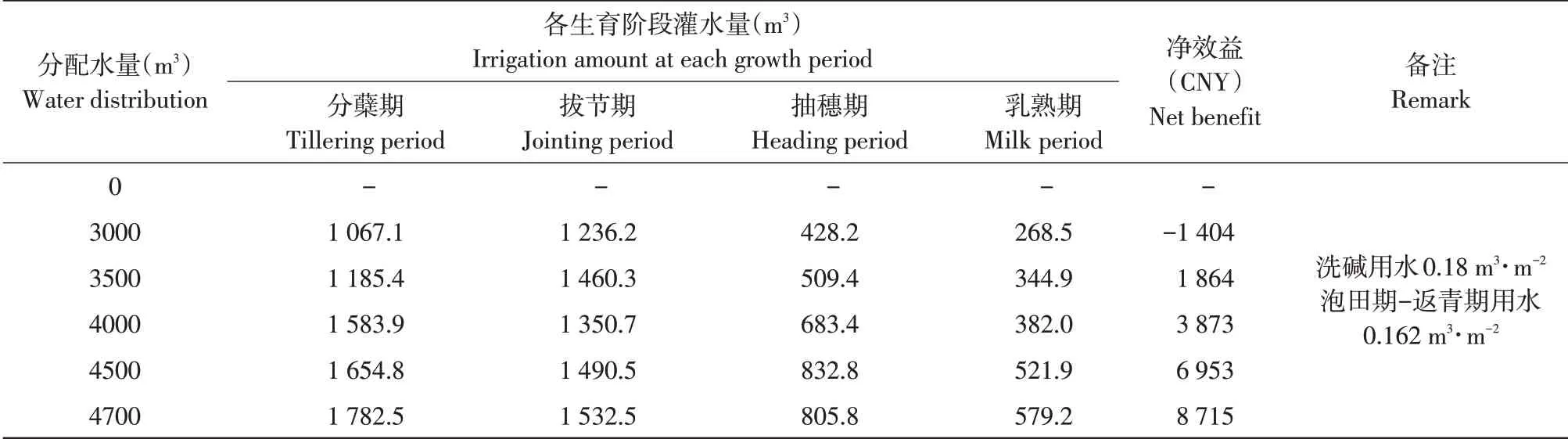
表4 泰来灌区水稻非充分灌溉制度优化成果（P=50%）Table 4 Optimization results of insufficient irrigation system for rice in Tailai Irrigation District

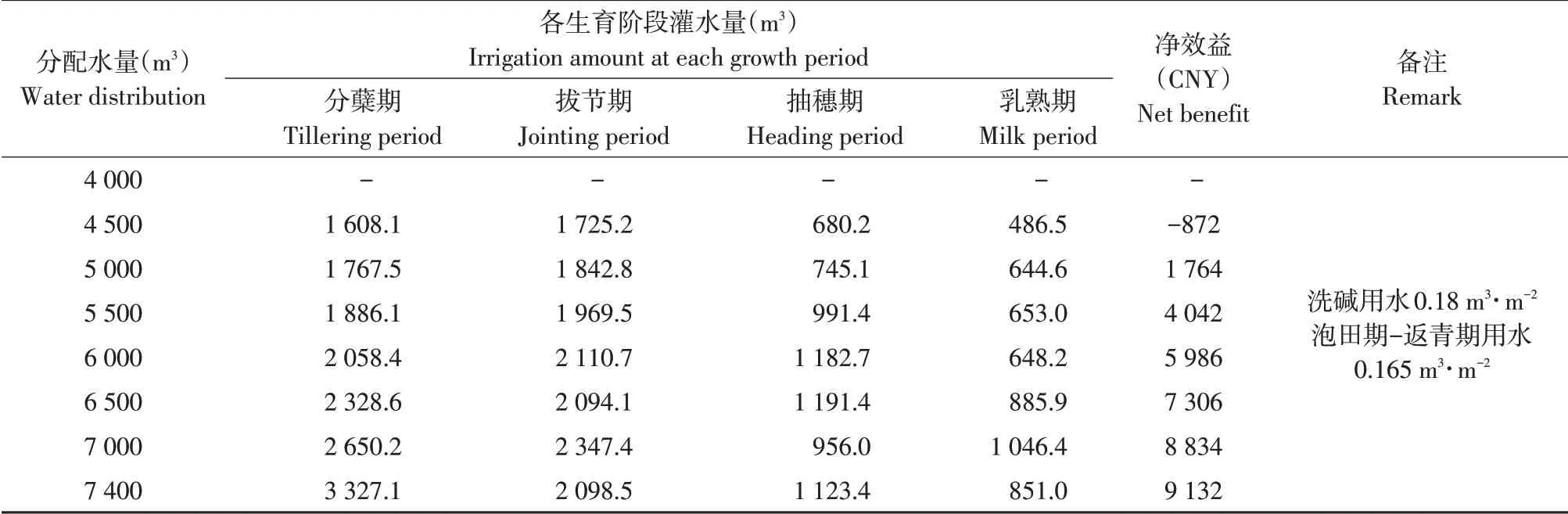
表5 泰来灌区水稻非充分灌溉制度优化成果（P=75%）Table 5 Optimization results of insufficient irrigation system for rice in Tailai Irrigation District

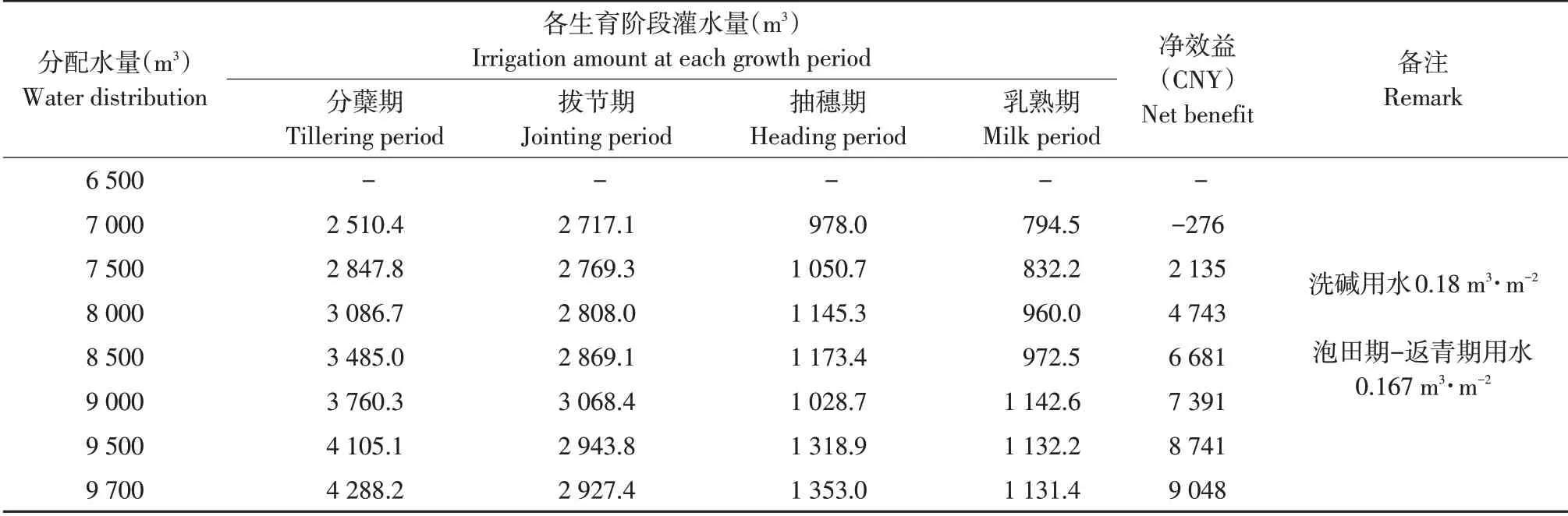
表6 泰来灌区水稻非充分灌溉制度优化成果（P=90%）Table 6 Optimization results of insufficient irrigation system for rice in Tailai Irrigation District

表7 基于ASGA的灌区水资源优化配置结果Table 7 Result of optimal allocation of water resources in irrigation area based on ASGA

由图4可知，当灌区分配灌溉水量较小时，灌区水稻净效益值随灌水量增加而大幅增加，这是因水稻在极度缺水情况下，每增加单位灌水量即大大提高水稻单位面积净效益。随灌水量增加，水稻净效益曲线坡度不断变缓，即灌水量对单位面积经济效益影响因子逐渐减小，当灌溉定额为8 220 m3时，单位面积净效益达到最大值。

保证率P=50%情况下单位灌水量净效益随单位灌水量变化见图5，由此可见，随灌区灌水量增加，单位灌水量产生单位面积净效益值增加梯度逐渐减小，当灌水量达8 000 m3时，单位水量所产生净效益接近峰值，此时再增加灌水量时，单位水量净效益值出现下降趋势。

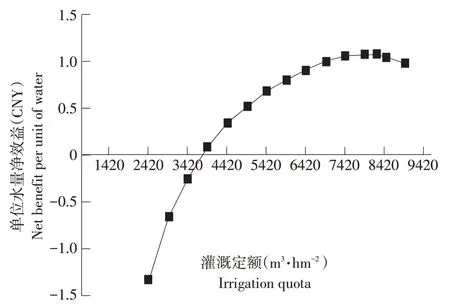
图5 单位灌水量经济效益随单位灌水量变化（P=50%）Fig.5 Economic benefit of unit irrigation volume varies with the unit irrigation volume

5 结 论

a.本文充分考虑灌区灌溉水量对作物各生育期的影响，建立基于单位面积经济效益最大的动态规划模型，运用ASGA 优化算法对目标函数求解，结果表明，该模型与算法适合该灌区水资源优化配置。对比张帆等以经济效益、社会效益、生态效益为目标函数构建的多目标优化模型[1]，本模型对经济效益单目标优化结果更好，但优化目标单一，无法衡量灌区整体效益。对比杜丽娟等构建的GWAS 模型[2]，本模型优化效率更高，但也与其存在类似情况，因分析频率对象较少，无法真实反映情况，易出现偏差。

b.泰来灌区水资源量丰富，为当地水田种植提供充足资源，灌区水源有保证。在不同灌溉设计保证率情况下，随灌水量增加，灌区单位面积净效益呈上升趋势，但提升幅度逐渐减小，说明在灌区灌水量逐渐增加情况下，供水量对单位面积净效益的影响因子越来越小。所以通过增加灌水量提高灌区整体经济效益的方法并不可取，在水资源不足或水价上涨情况下，采用非充分灌溉制度更为合理。

c.本研究采用ASGA 优化算法具有一定创新性，解决传统算子陷入局部最优解的问题，且模型计算速度快、优化效率高、方案新颖，有较高实用价值。本文也有不足之处，未考虑水价变化因素，未来研究可将水价因素并入优化算法中进行灌区整体水资源优化配置，且优化目标单一，加入生态效益、社会效益等目标组合成多目标优化算法。