大型复杂枢纽列流图的列流线排列优化算法
耿敬春,倪少权,李建新,吕苗苗
(1.西南交通大学 交通运输与物流学院,四川 成都 610031;2.中国铁路经济规划研究院有限公司 线路站场咨询部, 北京 100844;3.西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 610031;4.西南交通大学 综合交通大数据应用技术国家工程实验室,四川 成都 610031)
铁路列流图是铁路建设项目运输组织设计的重要内容之一,是反映某个铁路枢纽、车站(技术作业站、客运站等)及衔接的各方向铁路线,在一定时间(一般指一昼夜)内上下行方向到发各种列车列数的示意图形;一般用不同类型的线条符号和颜色表示列车种类,附加以数字表示列车数量,沿铁路线依次铺画。针对单一铁路线或简单的铁路枢纽,设计人员基于AutoCAD手工逐一铺画列流线较为简单、方便。大型复杂铁路枢纽具有车站数量多、车站分工复杂、衔接铁路线多、列流线多等新特点,基于AutoCAD手工编制列流图的效率和质量已不能适应勘察设计要求。列流图编制主要包括枢纽铁路线路与车站拓扑关系、列车开行方案(即列流线)和列流线排列3个方面。其中,铁路线路与车站拓扑关系由枢纽布局形态确定;列流线设计主要包括始发站、终到站、列车种类、经由径路和列车数量等,一般根据客货运OD(Origin-Destination)按照一定规则设计。
目前,我国对列流图的优化研究取得了一定成效。史峰等[1]提出列流图的左右、紧凑、分层、对称和分类5种排列原则,当排列原则相冲突时,除对称和分层排列原则外,应遵循分类、左右、紧凑排列的先后顺序。文献[2-5] 给出了折点、径点、拐点和描绘点等术语定义;借鉴最短径路算法,提出铁路路网点集合描绘思路、列流线自动描绘的标号算法思路、站点连通路径标号算法、点集合及边集合自动生成算法、列流线折点搜索算法、列流线偏移描绘算法等。这些研究为实现计算机自动编制列流图提供了技术支持。鉴于大型复杂枢纽内车站数量多、衔接方向多、列流线多等新特点,本文在大型复杂枢纽线路与车站拓扑关系、大规模列流线既定的基础上,研究基于“通道法”的列流线在各铁路线和车站的互相排列优化问题,以提高大型复杂枢纽列流图的编制效率和编制质量。
本文仅研究基于给定列车开行方案[6](始发终到站、列车种类、经由径路、列车数量)条件的列流线排列优化问题,对客货车开行方案[7-12]具体设计过程将另行研究。
1 问题描述及概念定义
1.1 符号设定及说明
列流图主要包括车站及衔接方向、铁路线、列流线等基础数据。枢纽内铁路线与车站的位置布局及其衔接关系,形成了复杂的拓扑关系。列流线根据列车编组计划的要素[6],按照列车沿铁路线左侧行车的要求,沿着铁路线左侧依次从内侧向外侧紧凑排列。据此,给出了车站及其相关、铁路线、列流线等定义,车站相关定义见图1;根据列流线沿一系列具有特定特征两两首尾相衔接的铁路线外侧行进具有不改变排列关系的特点,给出了通道到发节点对集合的定义;相关的集合、参数符号及说明见表1,变量符号及说明见表2。

图1 车站相关定义

表1 集合、参数符号及说明

表2 参数符号及说明
1.2 铁路线布局
由任意2个不相同的节点连接形成的边即为一条铁路线ri(铁路区间),ri满足ri=(gs,ls,k,gs′,l′s′,k′),∀gs,ls,k≠gs′,l′s′,k′。按前述车站相关概念,铁路线r1=(gs1,1,1,gs2,3,0)为水平布置、r2=(gs2,0,0,gs3,2,0)为垂直布置、r3=(gs1,0,0,gs3,3,0)为拐弯布置和r4=(gs1,0,1,gs1,1,0)为环形布置,见图2。
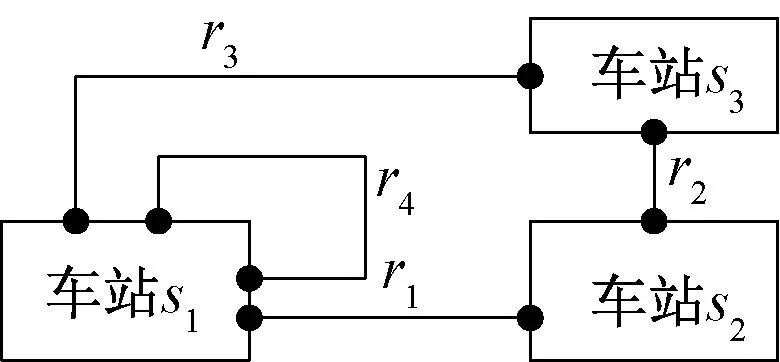
图2 铁路线布置形式
1.3 通道模型建立
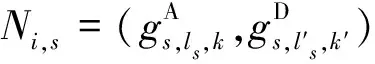
wi={Ni,s0,Ni,s1,…,Ni,sm}=
满足:∀m,|l′sm-lsm|=2,
[gsm,ls,k(x)=gsm,l′s,k′(x)∧(lsm=0∨lsm=2)]∨
[gsm,ls,k(y)=gsm,l′s,k′(y)∧(lsm=1∨lsm=3)]
通道构成示意见图3。图3中,由蓝色、紫色、红色、绿色铁路线共组成8个通道,如w0为由蓝色铁路线两两首尾相连接衔接的车站s1、s2、s3、s4对应节点对组成的通道,w4为其按列车运行的反方向组成的通道;w2为由红色铁路线两两首尾相连接衔接的车站s10、s6、s2、s3、s4对应节点对组成的通道,w6为其按列车运行的反方向组成的通道。

图3 通道构成示意

2 假设与通道集合求解算法
2.1 假设
假设1:排列在同一铁路线外侧的所有列流线相互之间的排列关系保持不变,且所有列流线均与铁路线按一定间距d的整数倍n距离平行排列。

假设2:排列在同一通道wi内所有铁路线外侧的所有列流线相互之间的排列关系保持不变,且所有列流线均与铁路线按d的n倍距离平行排列。

在假设1和假设2条件下,求解列流线的优化排列问题将化简为求解通道集合和求解列流线在通道wi中对应节点的占用状态集合元素的值。
2.2 通道集合求解算法
在求解列流线的优化排列问题,根据列流图中车站、铁路线布局,通道和通道集合的定义,构建通道集合W,求解算法如下。
Step1在铁路线集合R中任取一个铁路线ri=(gs,ls,k,gs′,ls′,k),将其作为通道wi经由的一个铁路区间;为使铁路线ri仅包含于一个通道中,将ri从集合R中剔除。以此铁路线衔接的2个节点为起始,按照Step2和Step4分别向两端建立到发节点对。
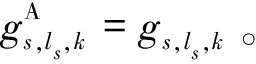
Step3在铁路线集合R中遍历所有铁路线,得到包含节点gs,l′s,k′的铁路线ri=(gs,l′s,k′,gs′,ls′,k)。若ri=Ø,终止顺向建立到发节点对;否则,将铁路线ri衔接的节点gs′,ls′,k代入Step2循环执行,同时在集合R剔除元素ri。

Step5在铁路线集合R中遍历所有铁路线,得到包含节点gs′,l′s′,k′的铁路线ri=(gs,ls,k,gs′,l′s′,k′)。若ri=Ø,终止逆向建立到发节点对;否则,将铁路线ri衔接的节点gs,ls,k代入Step4循环执行,同时在集合R剔除元素ri。
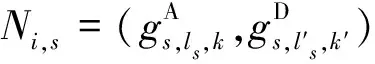
3 列流线排列优化算法
3.1 列流线的排列关系
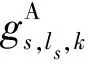
(1)直行最内侧原则


→列流线;--2条铁路线间接上下行线铺画的列流分割线。图4 列流线排列关系
(2)始发最外侧原则和终到最外侧原则
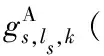
(3)到达节点列流线“逆时针”排列原则

(4)出发节点列流线“顺时针”排列原则

3.2 列流线的“通道法”排列优化算法
(1)“通道法”排列优化思路
由列车径路节点集合Pt和通道wi可知,任一列流线t的径路节点集合Pt是由一个或若干个通道wi的子集按列车运行方向先后经由的车站顺序排列构成的集合。如图5所示,列流线a的径路节点集合Pa由通道w1的子集构成,列流线b的径路节点集合Pb分别由通道w2、w1的子集构成,列流线c的径路节点集合Pc分别由通道w7、w1的子集构成,列流线d的径路节点集合Pd分别由通道w0、w3、w1的子集构成。因此,可将列流线的排列优化问题按经由的通道子集进行分段求解优化;如列流线d的排列问题将分解为在通道w0中车站s1至车站s2、通道w3中车站s2至车站s7和通道w1中车站s7至车站s9的3个排列问题。
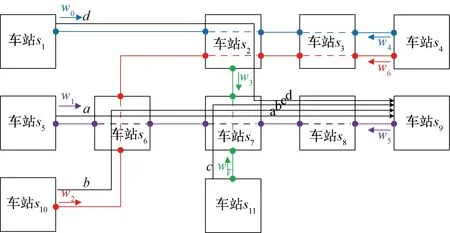
图5 通道列流线排列示意
(2)“通道法”列流线排列优先权重求解算法
在假定2条件下,将在同一通道内经由到发节点数量越多的列流线排列在越靠近铁路线的内侧,使得列流线布局越紧凑。因此,同一通道内的列流线需要按照优先权重的大小进行排列,权重越大的,越优先排列,且排列在内侧;否则,排列在外侧。求解算法如下。
Step1设置默认值。Zt,wi为列流线t在通道wi的排列优先权重;设置所有列流线的排列优先权重Zt,wi=0,∀t∈Twi。
Step2求解列流线排列优先权重。
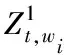

Step3求解通道wi内优先权重。

Step4求解顺向至终到站优先权重。


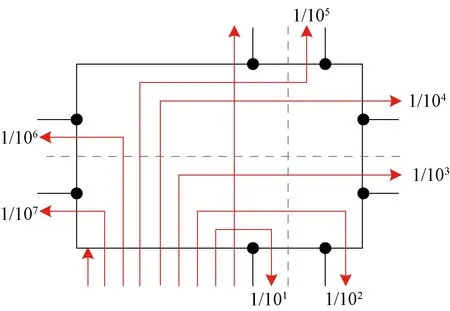
图6 到达节点列流线数量级
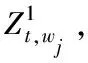
Step4.3循环递归执行Step4,顺向至列流线t的终到站时终止。
Step5求解逆向至始发站优先权重。
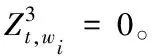
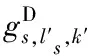

图7 出发节点列流线数量级
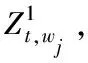
Step5.3循环递归执行Step5,反向至列流线t的始发站时终止。

(3)“通道法”列流线排列优化算法
在大型复杂铁路枢纽中,根据铁路线与车站的拓扑关系及布局,将其划分为若干个通道;以通道为单位,求解列流线在通道的排列优化,以达到整个列流图中列流线的布局优化。借鉴文献[13-14]思路,求解算法如下。
Step1根据车站、铁路线布局,按照通道集合求解算法,构建通道集合W;在通道集合W任取一个通道wi。若wi≠Ø,执行Step2,同时在W中剔除元素wi;否则,终止。
Step2按照通道列流线集合定义,求解Twi;若Twi≠Ø,执行Step3;否则,返回Step1。
Step3按照“通道法”列流线排列优先权重求解算法,求解通道列流线集合Twi中所有列流线的优先权重。取max(Zt,wi),∀t∈Twi;若t≠Ø,执行Step4,同时在Twi中剔除t;否则,返回Step1。
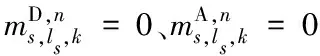
按照上述算法,求解图5中通道w1中列流线的排列优先权重如下:

4 上海铁路枢纽算例验证
以上海铁路枢纽客运列流图的编制对前述算法进行实例验证。上海铁路枢纽连接京沪高速、沪宁城际、南沿江铁路、北沿江铁路、沪昆高铁、沪杭城际、沪乍杭铁路、沪通铁路、沪苏湖铁路、京沪铁路、沪昆铁路、金山铁路、浦东铁路,共计13条线路。随着规划线路的引入,枢纽客运系统形成上海、上海南、上海虹桥、上海东以及上海宝山、松江南等“四主多辅”的客站格局。根据衔接线路所承担客流以及上海铁路枢纽客运需求,上海铁路枢纽规划年度始发客车对数详见表3,枢纽衔接4个方向间通过客车,始发、通过客车主要见表4,规划年度远期始发、通过客车主要客站分工及作业量见表5、表6。
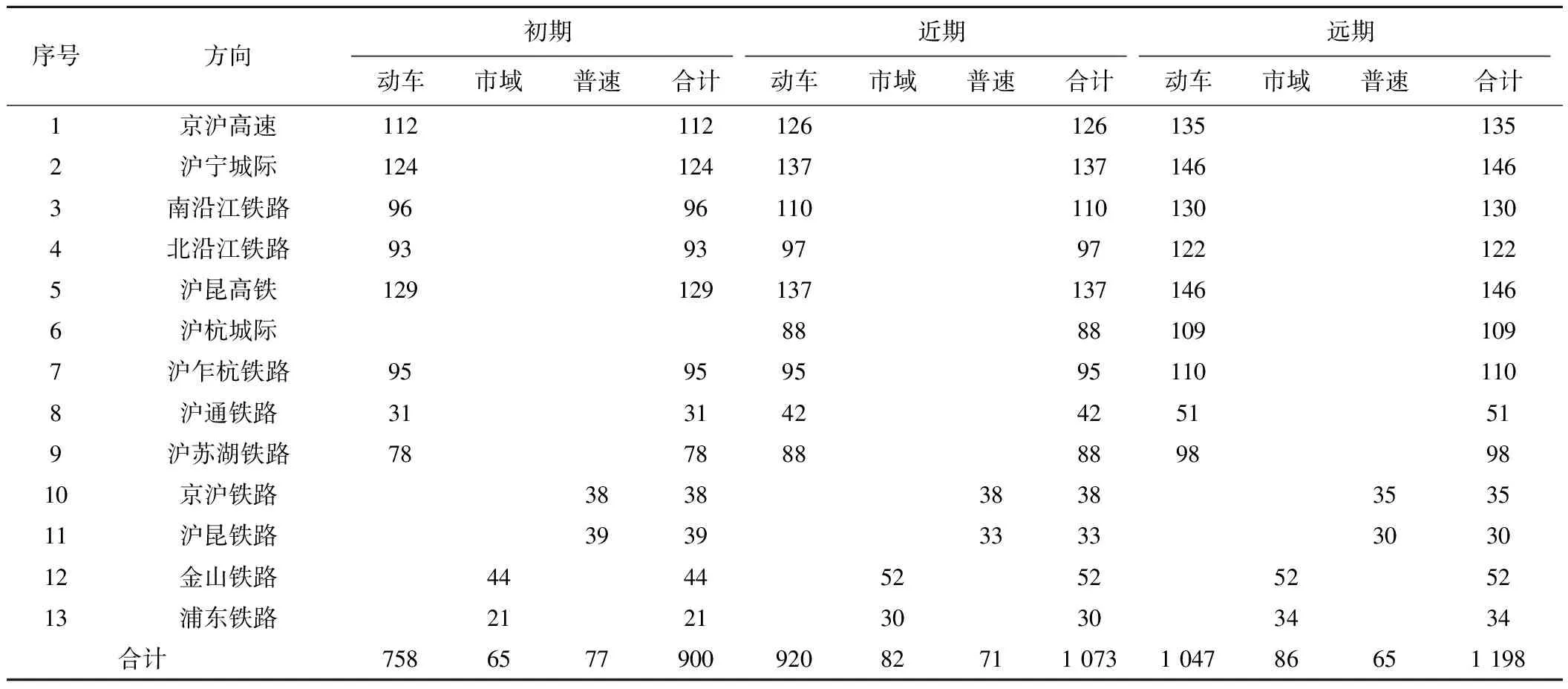
表3 规划年度始发客车对数表 对/d

表4 规划年度通过客车对数 对/d

表5 规划年度远期始发客车主要客站分工及作业量 对/d
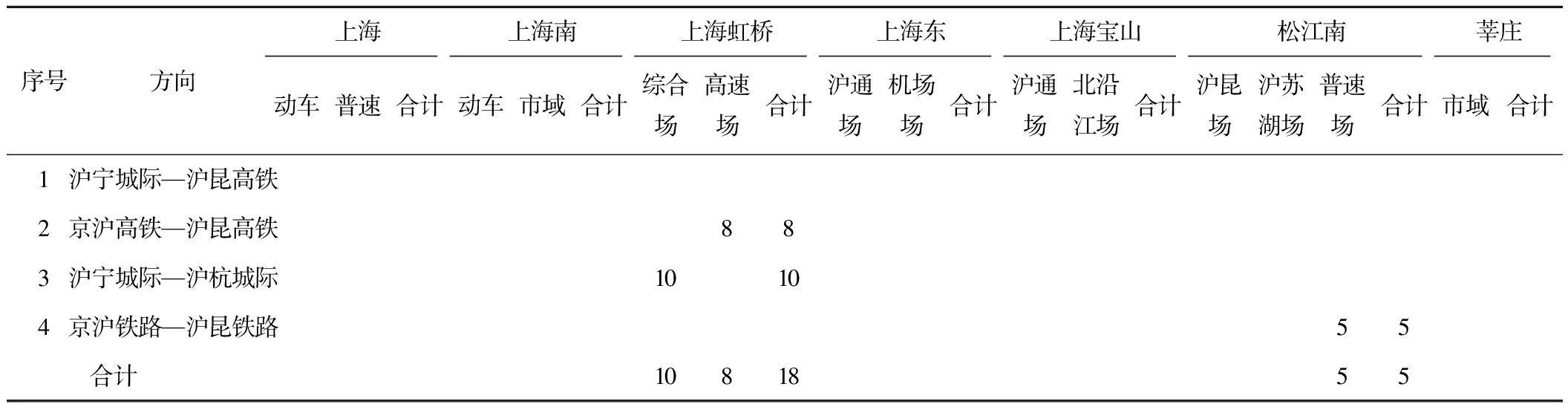
表6 规划年度远期通过客车主要客站分工及作业量 对/d

图8 规划年度客运列流
运用本文提出的算法,在Windows操作系统Visual Studio 2019开发环境下,使用C#编程语言[15]研发了大型复杂铁路枢纽列流图编制系统;利用该系统,以上海铁路枢纽为研究对象,根据表3~表6中的数据,编制了客运列流图,见图8。
在列流图编制过程中,为减少绘图图幅,可将具有相同列车径路的同种列车类型的列流线合并铺画,将另行研究。经人工核查,图8所示的列流图无列流线铺画和标识错误,验证了算法的合理性和有效性;在列流图的自动编制过程中,通道集合的求解和列流线的排列优化时间消耗均小于1 s,在运输组织设计中可以忽略不计,表明了算法的高效性。
5 结论
本文针对大型复杂铁路枢纽具有的车站数量多、车站分工复杂、衔接铁路线多、列流线多等新特点,为解决设计人员基于AutoCAD的手工编制列流图工作量大、效率低下、质量不高等问题,根据铁路枢纽内车站、铁路线之间拓扑关系以及车站衔接方向节点间的横纵坐标关系,提出了列流线直行最内侧、始发最外侧、终到最外侧、到达节点“逆时针”和出发节点“顺时针”6条排列原则和列流线沿铁路线、通道内排列关系不变的2个假定条件,构建了通道到发节点对集合的求解算法、列流线排列优先权重求解算法和排列优化算法。以上海铁路枢纽客运列流图编制为例,运用研发的列流图编制系统验证了算法的合理性、有效性和高效性,解决了手工编制存在的困难和问题,实现计算机自动编制大型复杂铁路枢纽的列流图。

