5 MW风力发电机叶片耦合模态颤振参数研究

张 颖， 安利强， 王璋奇

(1.华北电力大学 能源动力与机械工程学院，河北 保定 071003；2.河北大学 建筑工程学院，河北 保定 071002)

0 引 言

风力发电机叶片随着尺寸的增加，输出功率越来越大。风机的风轮直径从几m到170多m，实现发电量从kW级别增加到MW级别。现代商用5 MW风机叶片长度超过60 m，目前研发的额定功率为8～10 MW的风力发电机叶片长度超过80 m。增加叶片长度可以捕获更多的风能，同时也带来了新的挑战。本文研究这类细长的柔性叶片，随着长度的增加，可能发生气动弹性不稳定性问题[1-3]。未来的风力发电机重要的工程问题是如何考虑叶片的柔性对气动弹性不稳定性的影响[4]。

大型风力发电机叶片是具有高纵横比的柔性叶片。柔性叶片及其周围流动之间的高度非线性相互作用导致叶片出现各种动态不稳定性[5，6]。

20 kW风力发电机刚性叶片的颤振速度比其正常运行速度提高几倍，而1.5 MW柔性叶片的颤振速度大约是正常运行速度的1.75倍[7]。由于叶片长度的增加，颤振速度更接近叶片的正常运行速度，因此在运行过程中更容易出现颤振。Hansen[8]回顾了现代商业风力发电机可能发生的两类气动弹性问题，失速型风机的失速颤振和变桨距风机的经典颤振。指出经典颤振可能是在附着流状态下运行的变桨距调节变速风机叶片的动态不稳定性。颤振可能发生在承受气动载荷的柔性结构中，并且由两种结构模式的结合引起的。已有文献风机叶片运行中，经典的气弹颤振不是风力发电机设计的首要因素，但是随着叶片越来越大和越来越柔，颤振在实际风机叶片中已经逐渐成为设计的考虑因素。为了研究颤振发生时刻的特征，对于线弹性模型，随着叶片长度增加，预测叶片颤振速度与风轮运行转速比越来越低，叶片在运行期间发生颤振的可能性增加[8，9]。Pourazarm[10]等人研究了扭转和挥舞的固有频率对临界颤振速度的影响。研究表明，在扭转固有频率不变的情况下，仅仅增加挥舞自振频率能够降低叶片的颤振频率。然而，扭转频率对于气动弹性稳定性的影响更为显著。随着扭转固有频率的降低，颤振甚至在低于额定速度的情况下发生。

一些研究人员使用各种分析工具量化MW级风机叶片的稳定性极限，Lobitz[7]基于NASTRAN对静止空气中的水平轴风力发电机叶片进行颤振分析，该模块最初是为分析垂直轴风力发电机叶片开发的。他研究预测WindPact 1.5 MW叶片临界颤振速度为42.3 r/m(是额定转速的两倍)，颤振频率为6.234 Hz。Lobitz[11]进一步研究缩比结构对风力发电机叶片稳定性的影响，对比研究长度为35 m的Windpact 1.5 MW 叶片和缩比后长度为9.86 m的GX-100叶片，缩比系数为0.271 8，设计相同的尖速比和展弦比，得出两支叶片单位转速下的颤振速度接近，进一步指出了Windpact 1.5 MW叶片在降低扭转频率与第二阶挥舞频率比和将叶片质心在弹性轴后移两种方式下，在较低的转速下发生颤振。Hansen[8]使用气动伺服弹性工具HAWCStab稳定性工具，研究了美国可再生能源实验室NREL5MW 叶片[12]的气动不稳定性，预测叶片颤振速度为24 r/m,是额定转速的两倍，进行了风轮颤振速度分析结果相似。Stablein[13]等研究了DTU 10 MW 风力发电机的模态特性和稳定性，他们使用气动伺服弹性工具HAWCSTAb2 ,通过稳态平衡下的特征值分析，研究了挥舞-摆振和扭转耦合的叶片。结果表明，当摆振-扭转顺桨耦合时，第一阶摆振模态的阻尼增加，而在摆振-扭转失速耦合时阻尼降低。挥舞-扭转顺桨耦合时，挥舞模态的频率增加，阻尼降低，然而对于挥舞-扭转失速耦合时，挥舞模态的频率降低，阻尼增加。Owens 和Griffith[14]采用Blast设计工具预测Windpact 1.5 MW和SNL100叶片的颤振，分别在40.6 r/m(额定转速的两倍)和13.05 r/m(额定转速的1.75倍)观察到颤振现象。在我国某风电场，6 MW机组风轮最大直径达到百米级别，发现某长度大于70 m的叶片由于振动发生损伤，发现损伤叶片时间处于挂机后尚未并网投运前，或并网投运最初三个月内。位置集中于叶身中段后缘区域，主梁和后缘完好，但蒙皮区域发生了类似失稳表象的破坏，叶片最终破坏形式是解体式的破坏，解体后叶片各部位保持相对的完整。以往文献中仅仅研究一两个参数，未对叶片的结构参数深入研究。

本文主要研究NREL 5 MW叶片挥舞刚度、扭转刚度以及叶片的质量矩、重心偏移等几个参数的变化对叶片颤振的影响规律。利用哈密顿原理推导弯扭耦合连续梁偏微分方程，结合Theodorson非定常气动荷载，求解复特征值方程，得到叶片颤振发生时刻的颤振频率和颤振速度。按照不同翼型族将风机叶片结构参数分成三个区域，通过数值分析，研究区域化结构参数变化对叶片耦合模态颤振的影响规律。

1 风力发电机叶片的气动弹性模型

气动弹性模型由两部分组成：结构模型和气动模型。在结构模型中，欧拉-伯努利梁，因细长的结构广泛用于风力发电机建模，利用哈密顿原理导出相应的控制微分方程，采用西奥道森理论求解非定常气动荷载的计算。

1.1 结构模型

基于Hodges[15]给出的悬臂旋转欧拉-伯努利梁的运动微分方程，假设梁是各向同性，在恒定角速度下的挥舞弯曲，摆振弯曲，拉伸和扭转运动微分方程，坐标系(XYZ)表示刚性连接到叶片根部的主体坐标系，X轴对应于未变形叶片的弹性轴，Y轴位于旋转平面内，Z轴垂直于旋转平面，如图1所示。点O为未变形弹性轴，O’为变形弹性轴，位移分别为u,v,w，其中，u,v,w分别代表轴向，挥舞和摆振方向位移。它绕变形的弹性轴旋转，角度β表示叶片的几何桨距角，是扭转和预扭转角的总和。

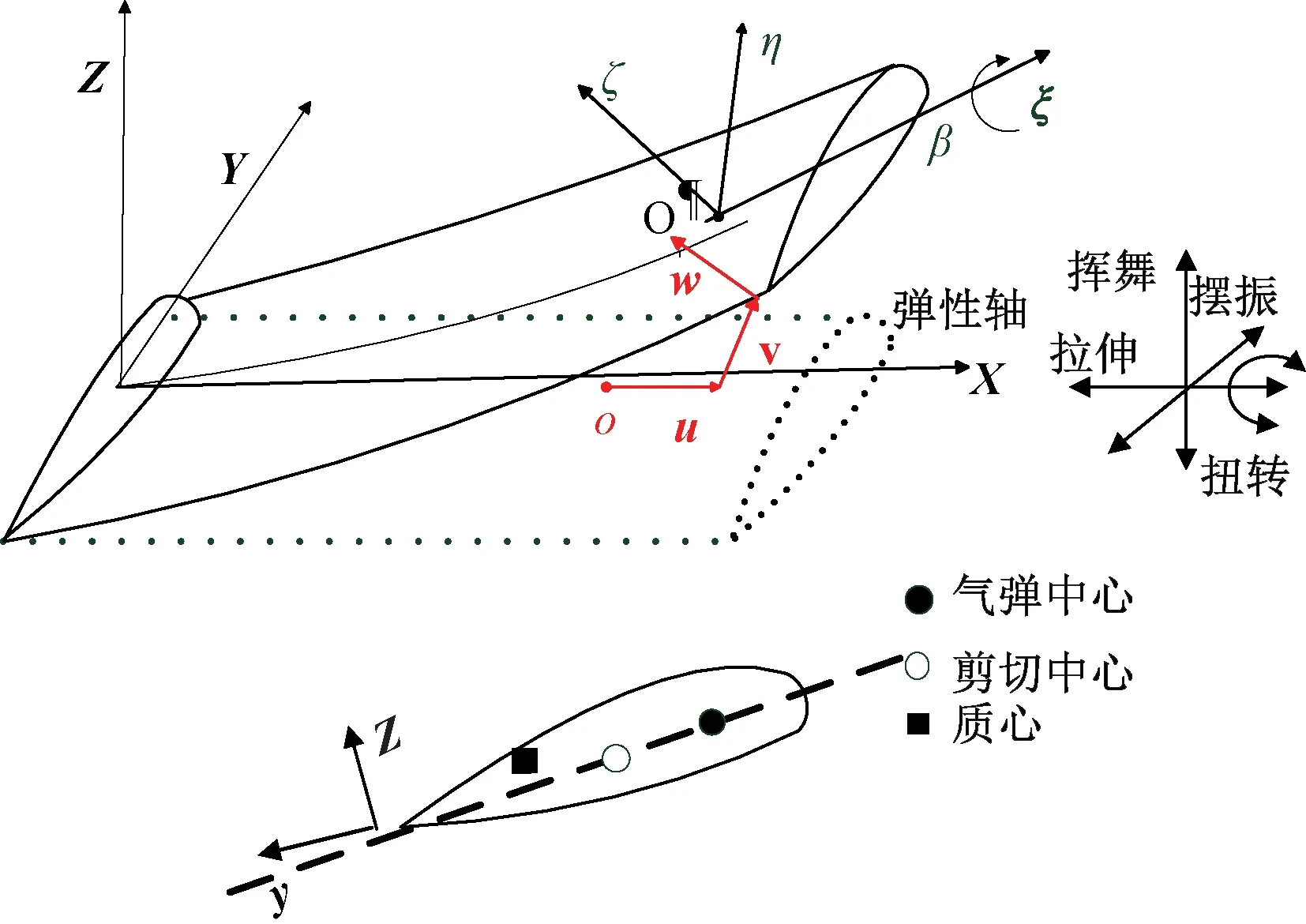
图1 叶片坐标系及其弹性位移Fig. 1 Coordinates of blade and its elastic displacements

与变形叶片的横截面正交的局部坐标系是ξ,η,ζ，其中ξ轴与偏转的弹性轴相切，η和ζ是截面的主轴。

如图1所示，其中，X,Y,Z是参考轴，旋转桨叶的建模考虑了挥舞弯曲和扭转两个方向的运动。运动方程是由哈密顿原理导出

(1)

式中：δU为应变能的变分；δT为动能的变分δW是做的虚功。Hodges和Dowell针对考虑各向同性风轮推导了δU和δT。Hong和Chopra修正了考虑复合材料正交各向异性的方程。仅仅考虑挥舞弯曲和扭转的复合材料风机叶片控制微分方程如下：

(2)

(3)

边界条件为

x=0,w=0,w′=0,φ=0x=L,w″=0,

w‴=0,φ′=0

(4)

式中：ω和φ分别代表挥舞和扭转位移；GJ是扭转刚度；EI是挥舞弯曲刚度；Km是绕弹性轴的极回转半径；Km1和Km2分别是绕主中性轴和垂直于弹性轴的轴质量回转半径；m为单位长度的叶片质量；ρ为叶片的密度；A为横截面积；e为质心偏移量，弹性轴和质心的距离；Ω为风轮转速；L和M为气动载荷作用在叶片上产生的气动力和变桨距。

1.2 气动载荷

结合Theodosen理论[16]，非稳态气动载荷在2D翼型上作用的变桨距M和升力L如下式：

(5)

(6)

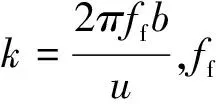
2 风力发电机叶片颤振速度计算方法

将方程(5)和(6)代入到(2)和(3)中，结合有限元方法，将叶片看作变截面线性欧拉-伯努利梁，每个节点自由度为3个，分别为w,δw/δx,φ。方程(2)，(3)的变分形式要求单元的插值函数连续，并且φ一阶导数非零，w二阶导数非零。结构区域离散为1维2节点单元，每个节点自由度的φ(x) 和w(x)分别假设为线性函数和三次多项式。

(7)

代入(2)和(3)，利用 Galerkin 方法[17]，在单元上加权积分，得到如下微分方程。

(8)

式中：Ms和Ma结构和气动质量矩阵，Ca为气动阻尼矩阵，Ks和Ka是结构和气动刚度矩阵。方程(5)和(6)是颤振频率ff的函数，方程(8)通过迭代方法求解复特征值问题，得到颤振频率和颤振阻尼。阻尼比计算利用复特征值的负实部除以复特征值的模得到，阻尼比变为零表示发生颤振。颤振发生的频率和速度定义为颤振频率和颤振速度。通常认为阻尼比为负值时，容易发生颤振，因为叶片要不断从空气中吸收能量，积累到一定程度会产生气动弹性不稳定[18]。颤振频率发生在第一阶扭转和第三阶弯曲模态耦合的时刻，此时，颤振速度对应气动阻尼比为零。

3 5 MW风力发电机叶片颤振分析

3.1 5 MW风力发电机叶片颤振速度

利用文献[12]的叶片翼型参数和截面特性，编制MATLAB有限元颤振分析程序，计算结果如表1和表2所示。表1中的自振频率为固有频率，和已有文献对比，表明程序设计正确，表2中为颤振频率与颤振速度对比，与Pourazarm[10]计算结果接近。

如图2所示，叶片随着转速的增加，颤振频率和气动阻尼的变化规律，在转速21.4 r/m时，一阶扭转模态和三阶挥舞弯曲模态耦合，负阻尼产生时对应的颤振频率为4.7 Hz。

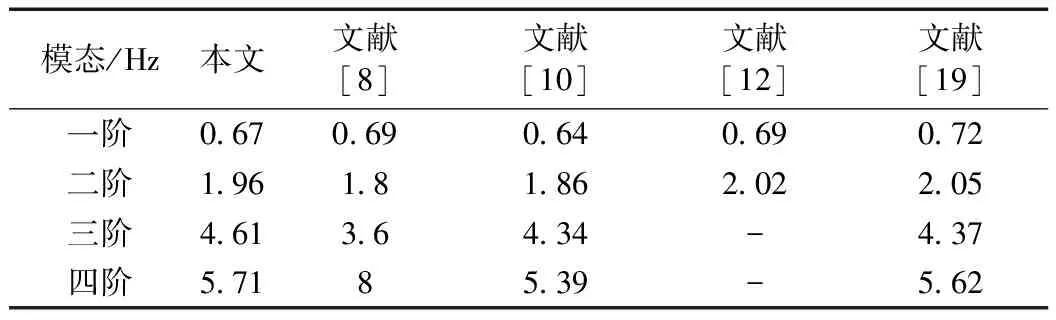
表1 叶片自振频率Tab.1 Comparison of natural frequencies

表2 叶片颤振速度和颤振频率Tab.2 Comparison of flutter speed and frequencies

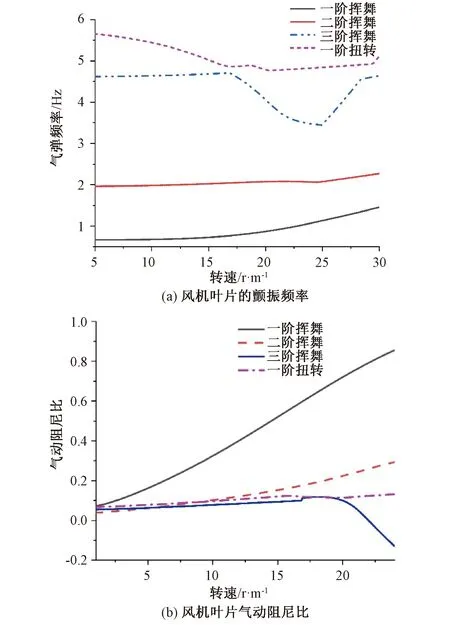
图2 5 MW叶片颤振频率和阻尼比Fig. 2 Damping ratio and aeroelastic frequency of NERL 5 MW wind turbine blade

3.2 叶片结构参数对气动弹性稳定性影响

风力发电机叶片的气动弹性不稳定现象属于模态耦合，当叶片的第一阶扭转模态和某一阶挥舞模态发生耦合，则出现经典颤振。因此，如果结构的参数发生变化，即使相同的风速和攻角作用下，叶片的颤振频率将产生变化。大型风机叶片沿着展向，具有不同的翼型截面，每个翼型在梁帽、腹板、前缘和尾缘都具有不同的复合材料铺层。按照翼型特性，图3所示，将叶片分为三个不同区域，分别为叶根，叶中，叶尖区域。假设叶片的几何形状不变，作用在叶片上的气动力不变，本文对比研究不同区域叶片的结构参数变化，初步分析耦合模态颤振规律。

图3 叶片的不同区域Fig. 3 Different airfoil regions for 5MW blade

考虑到叶片的翼型截面特殊特性，主要从叶片抗弯刚度、抗扭刚度、质量矩，质心偏移量的变化等几个方面，分析结构参数变化引起的颤振频率及颤振速度变化规律。

(1) 挥舞刚度变化

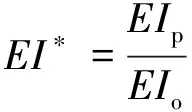
(9)

叶片简化为悬臂结构，按照悬臂梁理论，则有关系式(10)成立。挥舞固有频率和抗弯刚度EI平方根成正比，与单位长度的质量平方根、长度的平方成反比。假定其它因素不变，研究挥舞刚度变化引起的频率和转速。

(10)

根据式(10)，降低叶片刚度EI或增大叶片质量和长度，降低叶片的挥舞自振频率，表明叶片的挥舞方向更柔，相应图5的转速变化规律，图4中，当EI*<0.4,叶片的尖部对颤振频率影响较大，刚度减小至30%，叶尖颤振频率变化率最大约为71%。0.41三者接近，叶尖和中部区域对颤振频率的影响较大。

图4 颤振频率随挥舞刚度的变化图Fig. 4 Flutter frequency versus dimensionless flapwise stiffness

对于颤振速度，随着抗弯刚度的减小，对应的挥舞模态频率减小，和扭转模态耦合的时刻延后，因此颤振速度相对基准速度增大，当EI*<0.4，叶尖区域颤振速度变化为基准速度的1.15倍，叶根和叶中区域颤振速度保持在1.34倍。EI*>0.4，叶根区域变化引起的颤振速度迅速减小至基准速度。叶尖和叶中区域的变化引起的颤振速度从基准速度的1.3倍逐渐减小至基准颤振速度，当刚度继续增加，颤振速度减小缓慢，趋于基准速度的0.9倍。

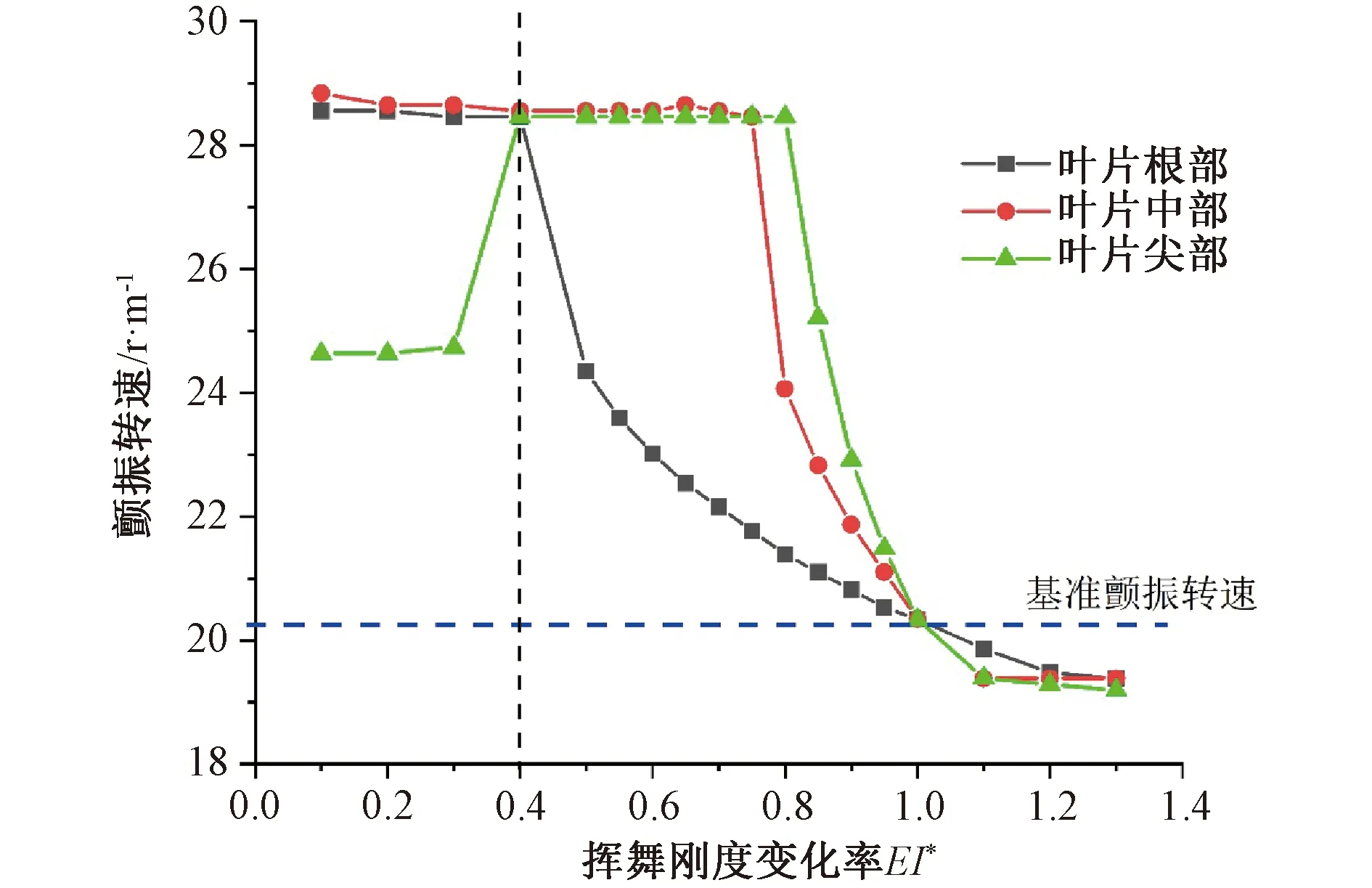
图5 颤振转速随挥舞刚度的变化图Fig. 5 Flutter speed versus dimensionless flapwise stiffness

(2)扭转刚度变化

定义无量纲扭转刚度为

(11)

扭转固有频率与扭转刚度的平方根成正比，与单位长度的质量平方根、长度和回转半径成反比，由式(12)可得

(12)

扭转刚度减小，扭转频率减小，不再是扭转和三阶挥舞模态耦合，而是扭转和二阶挥舞或一阶挥舞模态耦合产生的颤振.如图6，随着扭转刚度的减小，颤振频率逐渐减小，叶中和叶尖区域对颤振频率的影响程度接近。如图7所示，叶尖和叶中区域的颤振转速随着扭转刚度减小迅速减小，叶根区域减小缓慢。叶尖区域的扭转刚度对颤振速度的影响程度最大。

图6 颤振频率随扭转刚度的变化图Fig. 6 Flutter frequency versus dimensionless torsional stiffness

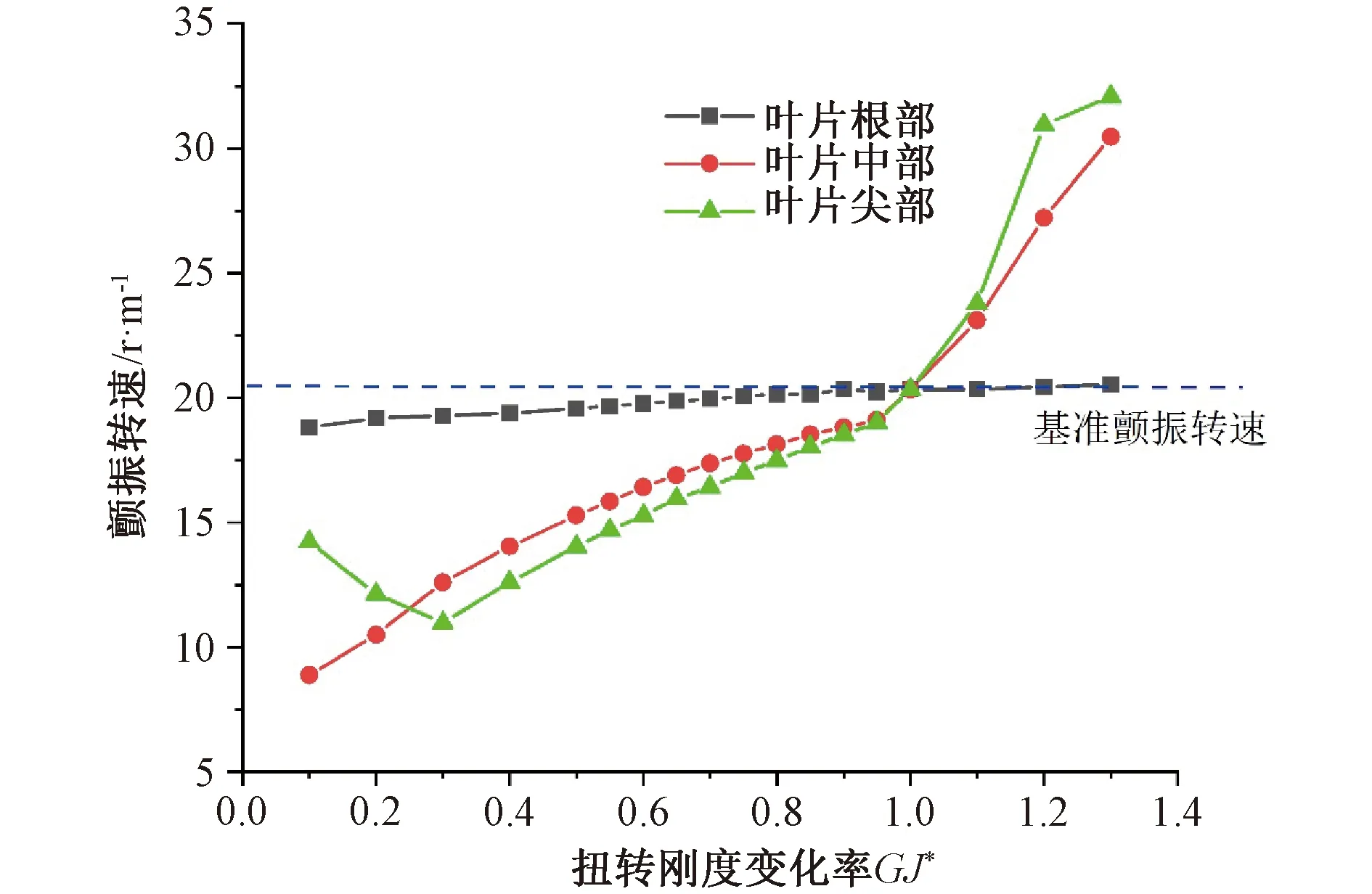
图7 颤振转速随扭转刚度的变化图Fig. 7 Flutter speed versus dimensionless torsional stiffness

(3)回转半径变化

叶片质量矩和回转半径平方成正比。因此，定义叶片对主中性轴和过弹性轴且垂直于弦的坐标轴的无量纲回转半径

(13)

公式(12)可知，扭转频率与极惯性矩Km成反比，回转半径Km1和Km2的大小反映了横截面的结构特性，体现弹性轴的质量分布特性，且有式(14)成立

(14)

分别改变对叶片截面的两个质量矩，发现对于叶片的截面的y轴的回转半径Km1*对颤振转速和颤振频率的影响较大。在Km1*=0.5时，达到最大值为基准频率的1.23倍。在Km1*>0.5时，随着回转半径的增大，颤振频率减小。说明对于截面的关于质量分布离弹性轴越远，更容易发生颤振。在区间Km1*<0.4，叶片中部和叶片尖部的颤振频率也随着回转半径增大而减小，总体频率均小于基准颤振频率，Km1*=0.4，叶中区域频率最小为基准频率的0.76倍。

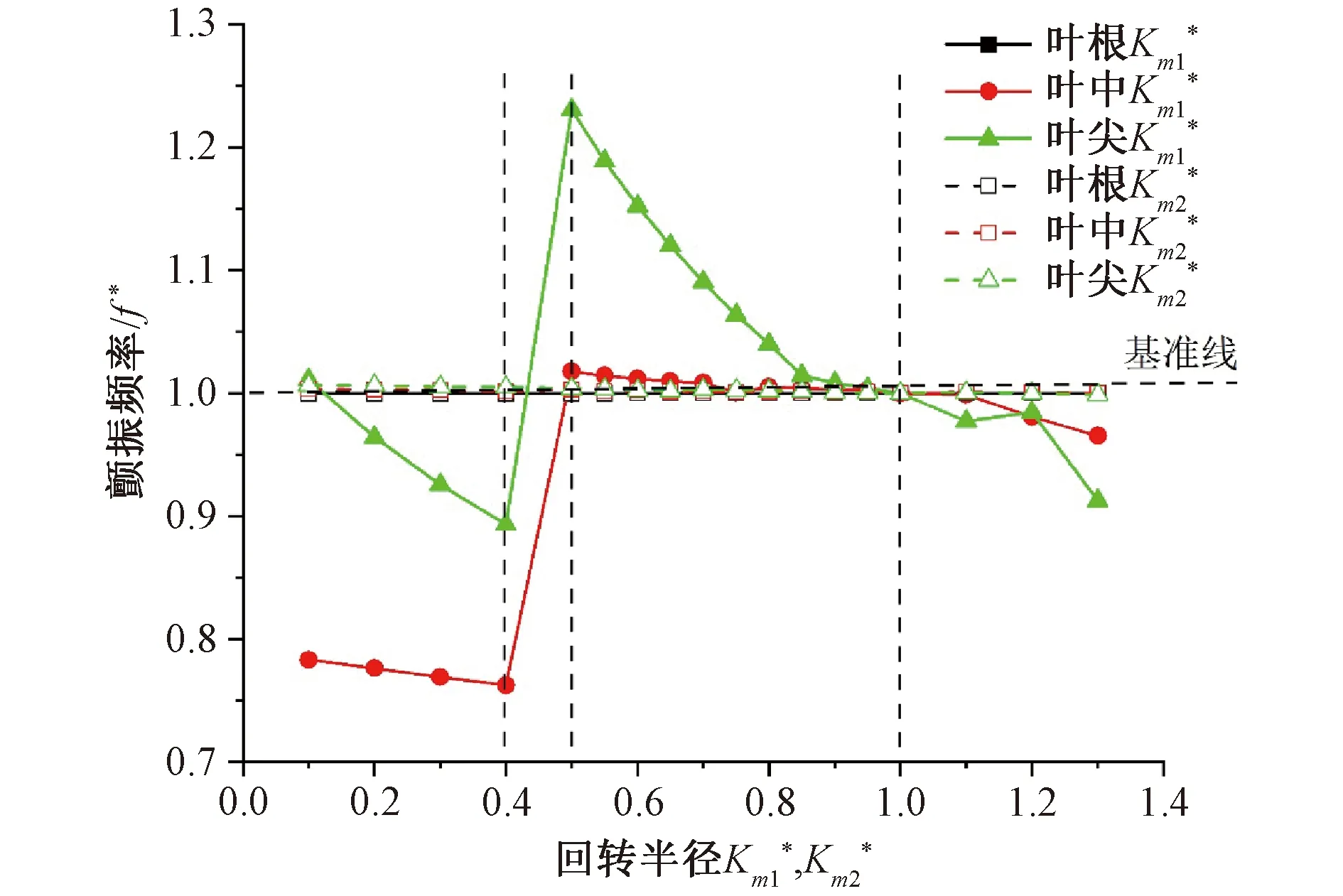
图8 颤振频率随回转半径的变化图Fig. 8 Flutter frequency versus radius of gyration

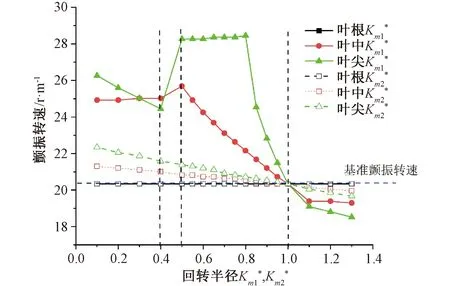
图9 颤振转速随回转半径的变化图Fig. 9 Flutter speed versus the radius of gyration

(4)质心位置变化

定义无量纲质心偏移量

(15)

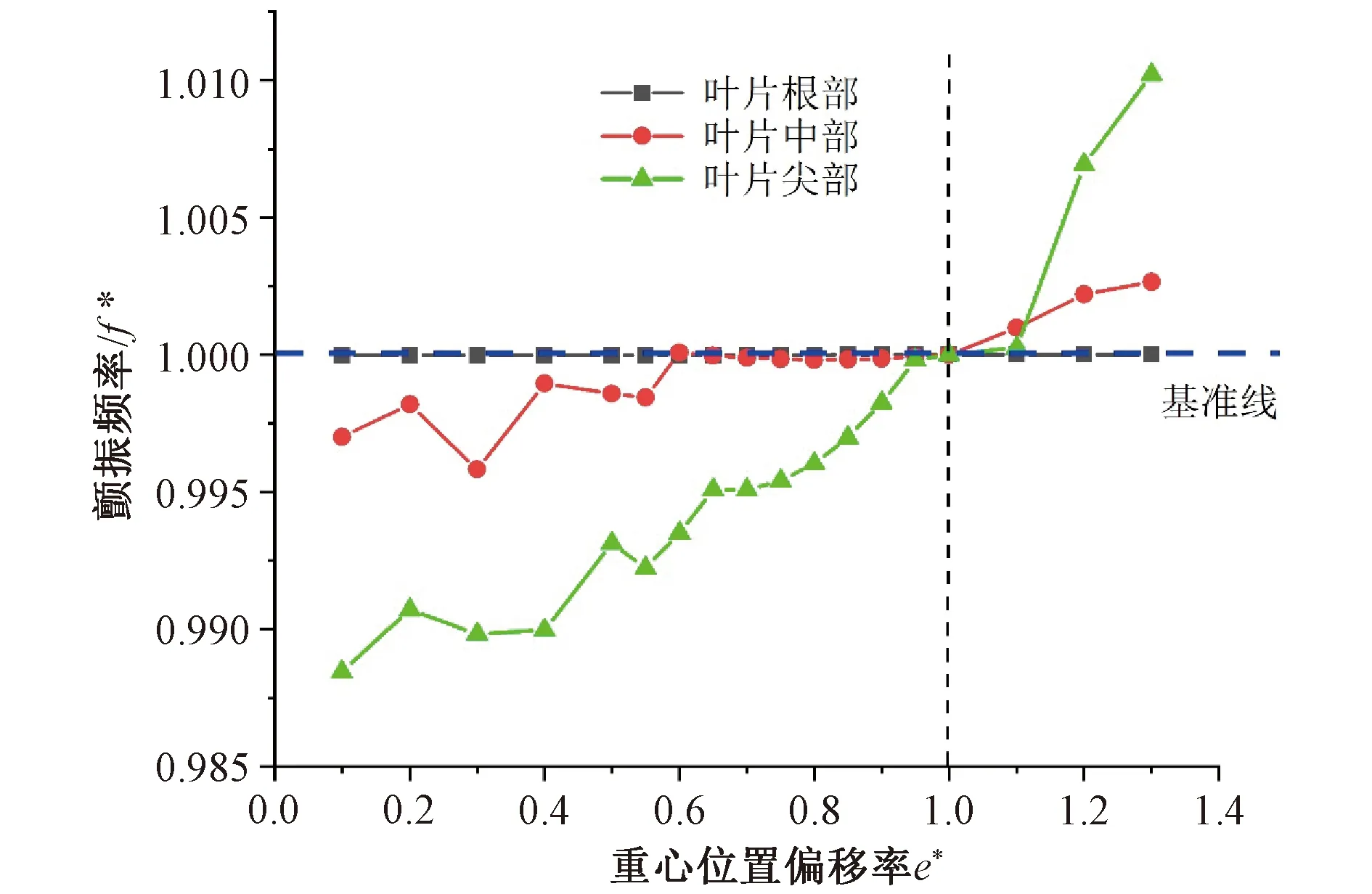
图10 颤振频率随质心的变化图Fig. 10 Flutter frequency versus mass offset

在叶片截面中，重心和弹性轴的距离e*，是一个影响叶片结构整体的动态不稳定性的参数。质心向叶片后缘移动，才可能发生颤振。由图10可见，随着质心偏移量e*增加，颤振频率略有增加，叶尖部位的截面影响稍微大些，最大颤振频率变化率仅仅2%。对于图11的颤振速度，叶尖部位影响较大，当减小e*，质心向尾缘后移，颤振速度减小，更容易发生颤振。

图11 颤振速度随质心的变化图Fig. 11 Flutter speed versus mass offset

4 结 论

本文通过对不同区域叶片参数变化，利用复特征值方法求解叶片颤振特征方程，对NREL 5 MW 风力发电机叶片的耦合模态颤振参数进行研究，验证了叶片第一阶扭转模态和某一阶挥舞弯曲模态耦合能引起颤振的现象。研究结果表明：

(1)通过分析叶尖、叶根、叶中三块区域的结构参数变化，叶尖区域的挥舞刚度对颤振频率影响较大，当挥舞刚度减小至30%，叶尖颤振频率变化率最大约为71%，颤振速度减小为基准速度的1.15倍，而叶根和叶中区域颤振速度保持在1.34倍。当挥舞刚度变化率从40%开始继续增加，叶根区域引起的颤振速度迅速减小至基准速度,叶尖和叶中区域的变化引起的颤振速度从基准速度的1.3倍逐渐减小至基准颤振速度，三个区域最终趋于基准速度的0.9倍。

(2)扭转刚度与颤振速度和颤振频率关系线性相关。叶尖区域的扭转刚度对转速影响较大，减小至30%出现转速突变。回转半径Km1*对颤振频率影响较大，叶尖区域的变化率为50%时，为基准频率的1.23倍，叶中区域变化率为40%时，为基准频率的0.76倍。回转半径Km2*变化与颤振速度和颤振频率近似成反比。Km1*在叶尖处存在一段增长缓慢区域达到基准速度的1.32倍迅速减小至基准速度。叶尖部位的质心偏移对叶片的颤振速度影响较大。

(3)对于MW级风机，叶片颤振问题，扭转频率和挥舞频率将成为未来设计的必要考虑因素。如何保持较高的扭转频率，避免和某一阶弯曲模态发生耦合，成为避免发生颤振的关键因素。