计及潜在道路和修复时间不确定性的电力应急物资输送路径优化
王志强, 王骁龙, 毛宇洋, 董忠涛, 刘文霞, 黄易君成
(新能源电力系统国家重点实验室(华北电力大学),北京 102206)
0 引 言
现代社会依靠电力不断发展,渐渐地已难以脱离电力而存在,如通讯系统、医疗卫生系统、交通信号系统等社会支撑力量离开电力供应将难以正常运行。然而,近年来地震、洪涝等自然灾害的频发对电力系统造成不同程度的破坏,伴随而来的便是巨大的损失[1]。灾害场景下电力应急修复是降低损失的重要手段,其中电力应急物资输送是应急修复基础,因此如何在复杂灾害路况下结合多源信息优化电力应急物资输送路径对提高电力系统韧性具有重要意义。
针对灾害场景下应急物资输送的路径规划方法,众多学者对其进行了研究。文献[2]考虑到应急物资需求程度的差异,以总延迟时间最短、软时间窗的惩罚成本最小和硬时间窗的不满足个数最少为目标构建应急物资车辆配送路径规划模型,规划结果有效提高了物资配送效率。文献[3]基于经典Dijkstra算法,结合道路中断概率对算法进行改进,不仅缩短了路径运输时间而且提高了规划结果的稳定性。文献[4]以运输时间、网络可靠性和运输损耗为目标,并考虑不同目标优先级,提出了灾后应急救援运输路径的多目标随机规划方法。文献[5]以路径效用和连通可靠性为目标建立双层规划模型,下层模型实现交通流分配,上层模型在下层目标基础上求取总目标最优,有效提高了应急救援工作的响应能力。上述文献均基于已有地图中的畅通道路进行规划,未充分利用具有通行潜力的潜在道路,并且未考虑道路抢修后投入使用对缩短输送路径通行时间的贡献,导致物资输送效率较低。
目前应急物资输送环节仍大范围采用避开道路障碍的方式,但随着通信网络逐渐发达和大数据等新兴技术的推进,应急部门和道路抢修部门联系日益紧密,可实现道路抢修部门协助应急部门开展应急物资输送工作,保证物资更快到达需求点。应急路径优化中考虑破损道路抢修的研究已有部分成果。文献[6]从占用物资、通行时间影响两方面特性对损毁道路修复、临时道路新修和较差道路平整三种修整工作进行分析,并建立了道路修整与应急车辆路径的集成优化模型。文献[7]利用物资要素和时延要素之间的转换,同时对路网结构和车辆路径进行优化。道路抢修包括抢修队前往路障和路障修复两个过程,上述文献认为只要抢修队到达路障,道路就转变为连通状态,未考虑路障修复时间[8]。文献[9]考虑应急抢通导致交通线通过性变化可能带来的影响,构建了最优救援路径和最优交通抢通方案双层规划模型。文献[10]基于道路系统抗震性预测,考虑震后不同阶段的道路抢修时间,提出了一种震后最优运输路径选择方法。上述两个文献考虑了路障修复时间,但未给出具体计算方法。实际场景中,一般由侦察人员依据现场情况一次性给定路障修复时间,但因为不同侦查人员在经验,认知等方面存在差异,使得判定结果因人而异,具有明显的主观性,并且此种方式中不良判定结果会导致规划结果产生较大偏差,鲁棒性较差,因此需要一种准确可靠的计算方法。
为此,考虑灾害场景下破损道路抢修的影响,本文提出一种计及潜在道路、路障修复时间不确定性的电力应急物资输送路径优化方法。首先,基于单兵轨迹信息,建立了轨迹点的道路匹配模型,并基于匹配结果给出潜在道路的筛选连接方法,得到计及潜在道路的应急增广电子地图生成方法;其次,基于增广电子地图,并考虑物资输送过程中对破损道路开展抢修工作,以期望通行时间最短为主要目标、路径长度最短为次要目标建立电力应急物资输送路径优化模型,其中为增强判定结果的鲁棒性,并削弱路障修复时间的传统判定方式的主观性,提出基于模糊理论的路障修复时间估算和物资输送路径期望通行时间计算方法;最后,利用改进遗传算法对所提模型进行求解,并且对比分析了潜在道路、修复时间不确定性和破损道路抢修对规划结果的影响,研究成果可以为灾害前期通信能力受限制的场景下进行离线路径规划提供参考方案,可有效提高电力应急物资输送效率。
1 计及潜在道路的应急增广电子地图生成方法
随着社会的不断发展,城市中封闭式小区大量出现,导致内部绿化走廊面积随之增加,同时小区围墙的拆除可成为沟通内部道路与外部道路的有效途径,除此之外,各种运动场、停车场等场地的围墙拆除也具有类似效果。视线转至农村,邻里巷道、干涸农田等具有通行潜力的场景众多。以上所有场景可统称为潜在道路,在灾害发生时经过不同程度的修整、加固均可成为运输车辆通行的备选道路,进而缩短路径通行时间,其中潜在道路的发掘由单兵完成,潜在道路的修整、加固工作由运输队利用随行携带的工具完成。本文将潜在道路的修整、加固时间计入潜在道路的通行时间,不再额外设立时间量。
基于单兵的轨迹信息,本章从单兵轨迹点的道路匹配和潜在道路筛选添加两个过程生成应急增广电子地图,其中前者得到最佳匹配道路,后者依据匹配结果筛选出潜在道路上的轨迹点,并连接成轨迹添加至已有电子地图上得到应急增广电子地图。
1.1 基于HMM模型的单兵轨迹点的道路匹配
单兵轨迹点以经纬度坐标的形式呈现,分为潜在道路上的轨迹点和已有电子地图的已有道路上的轨迹点两类,分别是单兵于潜在道路和已有道路上采集返回的轨迹点。其中,潜在道路上的轨迹点与已有道路之间的距离较大;已有道路上的轨迹点由于定位精度、传输误差等原因,与已有道路间同样存在距离,区别在于误差导致的距离较小[11]。道路匹配要解决的问题是在已知单兵轨迹的前提下,利用隐马尔可夫模型(Hidden Markov Model, HMM)将单兵轨迹点均匹配到已有电子地图,最后得到单兵轨迹点在已有电子地图中匹配度最高的最佳匹配道路。
地图匹配(Map Match, MM)技术是将采集得到的GPS点匹配到电子地图中的一项技术,减小定位结果与电子地图之间的差距[12]。HMM模型可以描述一个隐含未知参数的马尔可夫过程,其中预测问题的求解可以应用于MM技术,该问题已知可观测状态序列{Y1,Y2,…,Yi,…,Yn-1,Yn}、隐含状态序列{X1,X2,…,Xi,…,Xn-1,Xn}之间的状态转移概率P(Ski+1∣Sji)和隐含状态与可观测状态之间的观测概率Q(Yi∣Sji),其中隐含状态Xi(={S1,S2,…,Sj,…,Sm-1,Sm})表示可能与可观测状态Yi关联的隐含状态[13],预测问题通过求解可以得到概率最高的最优隐含状态序列。
本文基于HMM模型,考虑已有道路网络的拓扑连接关系,建立了如图1所示的道路匹配模型,其中可观测状态Yi表示第i个单兵轨迹点,隐含状态Xi表示第i个单兵轨迹点可能匹配的每条道路Sj。

图1 道路匹配模型Fig. 1 Road matching model

(1)

(2)
(3)

图2 垂直距离和夹角示意图Fig. 2 Schematic diagram of vertical distance and angle
其中,α、β分别表示垂直距离与方向夹角在匹配距离中的权重。

(1)初始化第一个可观测状态Y1的所有可能隐含状态的概率,并设置对应的前驱状态为0;
(4)
(5)
(2)递推计算其他可观测状态Yi的所有可能隐含状态的概率及前驱状态;
j=1,2,…,mi
(6)
j=1,2,…,mi
(7)
(3)比较最后一个可观测状态Yn的所有可能隐含状态的概率,将概率最高的隐含状态设为Yn对应的最佳隐含状态;
(4)根据所求的前驱状态结果,找出前面所有可观测状态的最佳隐含状态,即找到所有单兵轨迹点的最佳匹配道路[15]。
1.2 潜在道路的筛选及添加
基于匹配结果,并依据两类单兵轨迹点与已有道路间的距离具有明显差距的特征,筛选环节可以得到潜在道路上的轨迹点,连接后形成潜在道路的轨迹,最后通过添加环节将其添加至已有电子地图中形成应急增广电子地图。
文献[11]的思想与本文类似,其中筛选环节设定一个阈值作为全局标准,并将垂直距离大于阈值的轨迹点设定为失配点,若失配点连续则判定为潜在道路上的轨迹点。本文考虑到对相隔较远的单兵轨迹点进行定位和传输的硬件状态难以保持一致,使得轨迹点与真实位置之间的误差具有明显差距,因此通过将相邻单兵轨迹点的匹配距离差值与允许相邻轨迹点匹配距离差值ΔFlimit进行对比得到失配点,并设定最小潜在道路长度Llimit,将连续数量大于Llimit的失配点最终判定为潜在道路上的轨迹点,从而去除了失配点中的匹配失误点。
假设第一个单兵轨迹点为已有道路上的轨迹点,按如下步骤进行筛选:
(1)计算各单兵轨迹点与最佳匹配道路间的匹配距离。
(2)按照时间顺序,计算单兵轨迹点与上一轨迹点的匹配距离的差值,若差值小于ΔFlimit,则该单兵轨迹点与上一轨迹点同为已有道路上的轨迹点或失配点,否则与上一轨迹点属性相反。
(3)针对失配点,若失配点的连续数量大于或等于Llimit,则这一部分失配点为潜在道路上的轨迹点,否则为匹配失误点。
筛选得到潜在道路上的轨迹点集合后,先将潜在道路上的轨迹点按时间顺序进行连接,其次将两端的连接点垂直投影到最佳匹配道路上,最后将潜在道路的轨迹与连接点相连接即可形成应急增广电子地图。
2 基于增广地图的电力应急物资输送路径优化方法
2.1 考虑修复时间不确定性的应急输送路径优化模型
假设G=(E,V,W)是基于应急增广电子地图并根据单兵采集信息抽象出来的路网结构。E表示G中的节点集合(E={i1,…,in}),包含正常道路节点和路障节点两部分;V表示G中的边集合({i,j}∈V),具体为节点之间的路段,在本文中称为“道路”;W表示V的权重集合(wij∈W),若边{i,j}连通,则wij为道路的通行时间,具体为道路长度与运输车辆速度的商,其中考虑到灾害场景的紧急性,运输车辆速度设置为限速值,具体数值由单兵根据现场情况给定。
模型中其他参数和变量定义如下:
L1为运输出发点O到需求点D的某一物资输送路径,由道路的有序序列构成,R1为L1的集合;Xij为一个二元变量,当道路{i,j}包含在当前考虑路径L1中,取值为1,否则为0;ti为运输队到达但未通过节点i的时刻,Ti(ti)为ti情况下,运输队通过节点i的通行时间,其中正常道路节点的通行时间为0,路障节点的通行时间如式(9)所示;t0为运输队的出发时刻;Tmax为需求点要求运输队的最晚到达时间。
实际中难以保证运输队和抢修队于同一时刻出发,本文假设各抢修队于零时刻出发,运输队稍后再出发。应急输送路径优化模型综合道路的通行时间(wijXij)和节点的通行时间(TiXij)得到路径期望通行时间(具体计算方法见2.1.3),并以此为主要目标,求取期望通行时间最短的最优输送路径(Popt)。模型具体数学形式如式(8-12)所示,其中式(8)、(9)为目标函数,式(10-12)为约束条件。
(8)
Ti(ti)=max(T1i+T2i-ti,0)
(9)
s.t.
(10)
i,j=1,2,…,n,i≠j
(11)
(12)
式(9)中,T1i为抢修队从抢修出发点到达路障i的时间,具体计算方法见2.1.1;T2i为抢修队修复路障i所需要的时间,具体计算方法见2.1.2。
式(10)是不成环约束,限制运输队出发点O和物资需求点D不重合;式(11)是节点约束,保证道路两端节点i、j不重合;式(12)是硬时间窗约束,保证路径的期望通行时间不大于Tmax。
式(9)中,若路障i的T1i+T2i较长,不同输送路径到达该路障时均需要等待,通过该路障均需要时长ti+Ti=ti+(T1i+T2i-ti)=T1i+T2i,可能导致不同输送路径的期望通行时间相同,此时应以通行成本最低,即路径长度最短为次要目标,选出最优输送路径。
2.1.1 抢修队前往路障的时间T1i
针对T1i的计算,本文做出以下假设:
(1)各备选抢修出发点拥有足够抢修力量,可在零时刻向各待修路障派遣充足的抢修力量。
(2)各路障与两端最近的道路交叉口之间无其他路障存在,进而抢修队伍可以到达路障。

(13)
s.t.
(14)
p,q=1,2,…,n,p≠q
(15)
(16)

2.1.2 基于模糊关系理论的路障修复时间T2i的估算方法
以往一般由侦察人员一次性给定路障修复时间,但由于侦察人员在经验和对事物认知等方面存在差异,导致得到的结果具有明显的主观性。本文基于多名单兵及专家的综合判定信息,利用模糊理论中模糊关系的相关知识进行路障修复时间估算,保证估算结果可以较准确反映路障真实情况,从而提高路径规划结果的可靠性[16]。
设论域U={u1,u2,…,ui,…,uf},其中ui代表第i个路障;V={v1,v2,…,vj,…,vg},其中vj代表第j个路障修复时间,建立直积U×V={(u,v)∣u∈U,v∈V},并定义其中一个模糊子集R,即U到V的一个模糊关系,该关系具体描述为“修复路障ui需要时间vj”。关系程度由隶属函数R:U×V→[0,1]刻画,可表示为表1所示的模糊矩阵的形式,其中bij表示(ui,vj)对模糊子集R的隶属度。

表1 模糊矩阵BTab.1 Fuzzy matrix B
本文采用模糊统计法来确定隶属度,该方法基于模糊统计试验进行,试验步骤如下[17]:
(1)组织统计小组,要求统计小组的成员对模糊子集R的概念熟悉,并有用数量近似表达模糊概念的能力。
(2)针对直积U×V中某一个元素(ui,vj),每一个小组成员基于认知进行试验,判别该元素是否隶属于模糊子集R。
(3)统计结果,按式(17)计算(ui,vj)的隶属度bij。
(17)
(4)重复步骤2、3,计算U×V中每个元素的隶属度。
为保证试验结果的可靠性,试验总次数必须充足,因此设计统计小组由前方单兵和后方专家共同构成,其中后方专家通过前方传回的路障图片来进行判定试验。鉴于前方单兵基于现场情况进行试验,结果可信度高,因此给予单兵特殊的权重Q,并采用式(18)进行隶属度计算。
(18)
式中:P1ij、P2ij分别是单兵和专家判定“(ui,vj)∈R”的次数;N1ij、N2ij分别是单兵和专家针对元素(ui,vj)的判定次数。
由于时间紧迫性,实际中每个统计小组成员针对某个路障仅会给出一个修复时间,因此可以简化试验:每个小组成员针对每个路障仅进行一次试验,每次试验基于自我认知给出路障ui的修复时间vj。在统计试验结果时,试验(ui,vj)的结果为“(ui,vj)∈R”,而路障ui与其他时间vy的试验(例如(ui,vy),yj)的结果为“(ui,vy)不属于R”。
除此之外,考虑到部分修复时间对应的可能性过小,设置最小可能性bmin达到缩小修复时间集合的效果。
2.1.3 电力应急物资输送路径期望通行时间的计算方法
由于修复时间的不确定性,每一条运输出发点O到需求点D的物资输送路径(L1)的通行时间具有多种可能性,本文设置每一种可能的通行时间对应一条时空路径,即将每条输送路径依据可能的通行时间划分为多条时空路径[18]。
已知路网结构G中的边V的权重W和T1i、T2i,针对某一条输送路径,首先计算每条时空路径对应的通行时间及其可能性,然后将每条时空路径的通行时间进行线性加权得到该输送路径的期望通行时间。具体步骤如下:
(1)计算时空路径的通行时间:
1)首先按式(19)计算输送路径上的第二个节点的到达(但未通过)时间:
t2(t0)=t0+w12
(19)
2)逐一处理其他每一个节点i,判断上一节点的节点类型,并采取如下对应的计算方式:
①若为路障节点:由于某条时空路径在计算各路障修复时间时均只取定一种可能的情况,因此在取定的修复时间下,将抢修队到达路障节点i-1的时间T1(i-1)、路障节点i-1的修复时间u(i-1)和路障节点i-1的到达时间ti-1依据式(9)计算得到路障节点i-1的通行时间Ti-1,再加上路障节点i-1的到达时间ti-1和两节点之间的通行时间W(i-1)i,即可得到节点i的到达时间ti,如式(20)所示:
(20)
式中:u(i-1)1表示路障i-1的第1种可能的修复时间;mj表示路障节点j可能的修复时间数目。
②若为正常道路节点:将上一节点的到达时间ti-1加上两节点之间的道路通行时间W(i-1)i作为节点i的到达时间ti,如式(21)所示:
ti(to)=ti-1(to)+W(i-1)i
(21)
3)将物资需求点D的到达时间作为该条时空路径的通行时间。依据以上步骤可计算每条时空路径的通行时间。
(2)计算时空路径的可能性:
物资输送路径通行时间的不确定性是由路障修复时间的不确定性引起的,因此时空路径的可能性由路障修复时间的可能性决定。本文比较输送路径中所有路障节点在某条时空路径中所取定修复时间对应的可能性,将最小值作为时空路径的可能性。其中存在部分时空路径的通行时间相同的情况,仅需将其合并,可能性取最大值。
(3)计算各时空路径的权重wj:
式中:γk表示第k条时空路径的可能性;N表示某条输送路径对应时空路径的数目。
(4)计算输送路径的期望通行时间:
(23)
式中:Ts表示第s条时空路径的通行时间。
2.2 求解方法
2.2.1 求解算法
由式(9)可知,电力应急物资输送路径优化模型中,节点i的通行时间Ti与到达节点i的时间ti有关,即与运输队在节点i前方的通行情况有关,导致Dijkstra[19]、Floyd[20]等经典最短路径算法难以适用,因此本文选用遗传算法进行模型求解,将路径的节点序列设为染色体,其中的节点编号设为基因,进而通过比较一部分备选路径获得整个道路网络的最优输送路径。
实际道路网络中节点众多,但与节点关联的边数较少,属于大型稀疏网络,经典遗传算法无规律生成的种群大部分为无效路径,即路径的节点在实际道路网络中存在不相连的情况。为保证种群中均为有效路径,进而提高收敛速度,本文基于文献[21]提出的改进遗传算法,结合模型特征对经典遗传算法作了如下改进:
(1)基于可行性约束的初始种群生成:从起点开始逐一确定路径节点,通过搜索邻接矩阵并从关联节点中随机选取的方法确定,路径生成后检测路径可行性及是否与已生成初始种群重合。
(2)基于父代染色体重合特性的交叉算子:若父代染色体有重合基因,通过重合基因进行交叉。若父代染色体不具有重合基因,各随机选取一个基因进行交叉,如果子代染色体交叉处的两节点没有相连,则在不涉及子代染色体其他节点的前提下,按初始种群生成方法生成两节点之间的有效子路径并修正子代染色体。
(3)删减式变异算子:随机选取一个基因删除,如果子代染色体中删除位置前后的两节点没有相连,生成有效子路径进行修正。
除此之外,对于抢修队前往路障的时间T1i的计算同样采用本文所提遗传算法,其中适应度函数设置为抢修出发点到路障的路径通行时间。
2.2.2 求解过程
本文依据如图3所示的流程对电力应急物资输送路径优化模型进行求解。

图3 电力应急物资输送路径优化方法流程图Fig. 3 Flow diagram of transportation path optimization method of power emergency supplies
3 算例分析
3.1 仿真系统与参数
由于本文提出的电力应急物资输送路径优化方法依赖于单兵从灾害现场采集的信息,已有案例中难于找到完整的数据,因此本文首先拟定如表2所示的8条单兵探测轨迹(红色标记节点为路障,方框标记的道路为潜在道路),并在文献[8]构建的道路网络基础上添加探测轨迹中的潜在道路得到如图4所示的应急增广道路网络。

表2 单兵探测轨迹及模糊统计试验结果(单兵)Tab.2 Soldier tracks and its fuzzy statistical test results
表2中包含了关于路障修复时间的单兵判定结果,判定结果由括号中的数值表示。与之相对应的专家判定结果如表3所示。

表3 模糊统计试验结果(专家)Tab.3 Fuzzy statistical test results(expert)
应急增广道路网络中,已有道路通行时间如表4所示,潜在道路通行时间(包含潜在道路修整、加固时间)如表5所示。
求解算例的改进遗传算法采用Matlab脚本程序实现,其中设置交叉率为0.8,变异率为0.3,最大迭代次数为50,种群规模为300。
3.2 算例结果与分析
基于单兵和专家的判定结果,采用模糊统计法,可得到如表6所示的路障修复时间估算结果。
结合抢修队到达路障的时间计算得到输送路径的期望通行时间,并采用所提改进遗传算法求解得到如表7所示的最优应急物资输送方案。

表4 已有道路通行时间Tab.4 Travel time of existing road

表5 潜在道路通行时间Tab.5 Travel time of potential road

图4 应急增广道路网络Fig. 4 Emergency augmented road network
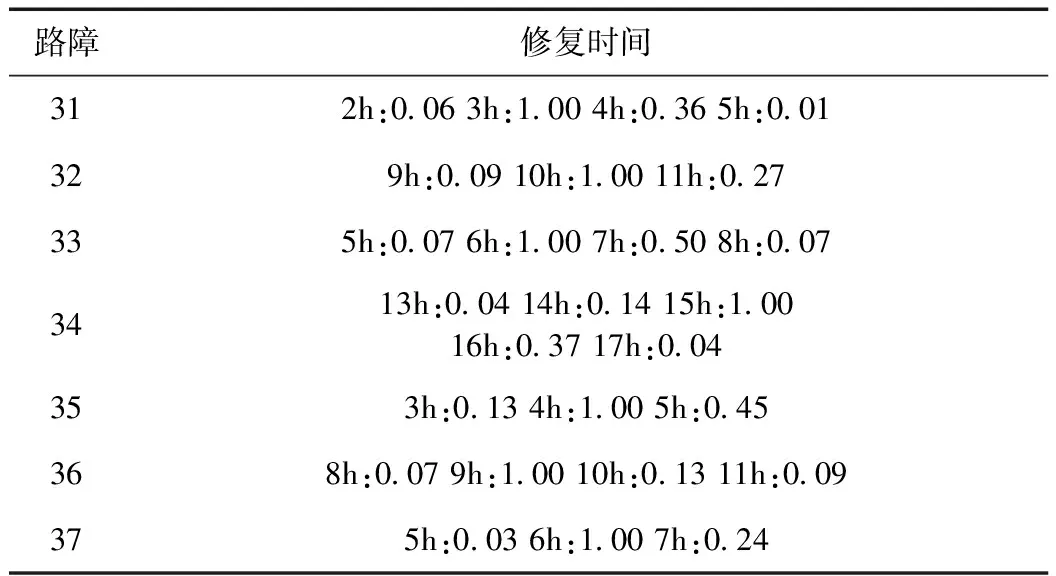
表6 路障修复时间估算结果Tab.6 Estimated repair barricades time

表7 电力应急物资输送路径规划结果
结果显示,最优输送路径为[1-13-2-3-31-4-5- 42-6-54-55-51-9-48-10-40-33-11-53-12](已在图4中标注),期望通行时间为29.28 h,路径长度为26.31 v(v表示平均车速)。
分析结果的过程中发现,存在与最优输送路径类似的输送路径,即[1-2-3-31-4-5-42-6-54-55- 51-9-48-10-40-33-11-53-12],期望通行时间比最优输送路径略多0.000 5 h,原因在于:子路径[1-2-3- 31]的通行时间为10.54 h,抢修队到达路障31需要8.52 h,由表6可知路障31的修复时间可能为2 h,8.52+2=10.52<10.54,运输队可直接通过路障,通过时间为10.54 h;最优输送路径的子路径[1-13-2-3-31]的通行时间为8.71 h,由于8.52+2 =10.52>8.71,运输队需要等待路障31修复完成后方可通过,通过时间为10.52 h,这种可能情况下的差别导致两条输送路径在期望通行时间上存在微小差距。除此之外,最优输送路径的路径长度少1.83 v,能有效降低运输车辆的通行成本。
3.3 潜在道路对输送效率的影响
为分析潜在道路对物资输送效率的影响,本文基于控制变量的思想设计对比场景1,该场景不再考虑潜在道路,道路网络对应于删去虚线道路和节点后的图4,并在模型求解时将遗传算法的种群规模设置为150。对比场景1的规划结果如表8所示。

表8 对比场景1的规划结果Tab.8 Optimization result of contrast scenario 1
对比场景1的最优输送路径为[1-13-2-3-31-4 -5-6-32-7-8-9-10-33-11-12],期望通行时间为 30.61 h,路径长度为26.74 v。与表7中算例的最优输送路径对比可知,潜在道路使得期望通行时间减少了1.33 h,路径长度减少了0.43 v,输送效率提高了4.34%,可更有效地保证电力应急物资的快速送达,并且可以节约一部分通行成本。
其中,潜在道路对路障的抢修路径同样具有优化作用。算例中路障32的抢修路径为[23-39-9- 51-55-54-32],通行时间为6.58 h;对比场景1中路障32的抢修路径为[23-9-8-7-32],通行时间为6.95 h。
通过对比可知,潜在道路54-55使得抢修队到达路障32的时间缩短了0.37 h,进而加快道路抢修进度,使得运输队更快通过路障32,可能达到缩短输送路径通行时间的效果。
3.4 修复时间不确定性对规划结果特性的影响
为分析考虑修复时间不确定性的效果,本文基于控制变量的思想设计对比场景2,该场景中各路障的修复时间取可能性最大的情况,即不考虑修复时间不确定性。对比场景2的规划结果如表9所示。

表9 对比场景2的规划结果Tab.9 Optimization result of contrast scenario 2
为分析修复时间不确定性对规划结果鲁棒性的影响,本文设置算例的对比试验,试验将某个单兵针对路障31的判定结果改为6 h(由表6可知6 h为不良判定结果),得到如表10所示的试验结果。同时设置对比场景2的对比试验,试验将路障31的修复时间改为6 h,得到如表11所示的试验结果。

表10 算例的对比试验结果Tab.10 Result of contrast test of example

表11 对比场景2的对比试验结果Tab.11 Result of contrast test of contrast scenario 2
对比表7与表10可知,不良判定结果使得算例最优输送路径的期望通行时间由29.28 h增加至29.36 h,改变了0.08 h;对比表9与表11可知,不良判定结果不仅改变了对比场景1的最优输送路径,并且通行时间由29.12 h增加至29.82 h,改变了0.7 h。
由上述分析可知:考虑修复时间不确定性可以减轻不良判定结果的影响,增强规划结果的鲁棒性,进而降低对单兵的要求。除此之外,模糊统计法判定修复时间的过程中征求多人意见,降低了传统判定过程的主观性。
3.5 破损道路抢修对输送效率的影响
若不考虑破损道路抢修,本文设置算例的对比试验2,得到最优输送路径为[1-14-16-20-24-57- 30-41-12],通行时间为35.91 h。与表7中最优输送路径相比,期望通行时间增加了6.63 h,破损道路抢修使得输送效率提升了18.46%。
因此应急部门应加强与道路抢修部门的合作,共同保证电力应急物资快速到达灾害现场。
4 结 论
为保证电力应急物资快速送达灾害现场,进而促进电力供应快速恢复,降低灾害给电力系统及社会带来的损失,本文首先基于单兵轨迹信息提出计及潜在道路的应急增广电子地图生成方法,然后基于增广电子地图,并考虑物资输送过程中对破损道路开展抢修工作,以期望通行时间最短为主要目标、路径长度最短为次要目标建立电力应急物资输送路径优化模型,同时提出基于模糊理论的路障修复时间估算和物资输送路径期望通行时间计算方法,并利用改进遗传算法对模型进行求解。通过算例分析,得到以下结论:
(1)充分利用潜在道路不仅可以缩短路障抢修路径的通行时间,进一步还明显缩短了电力应急物资输送路径的期望通行时间。
(2)综合单兵和专家判定结果的方式考虑修复时间不确定性是可行且有效的,规划结果可以容纳少数不良判定结果,提高鲁棒性,降低对单兵的要求,并且削弱了传统判定过程的主观性。
(3)破损道路抢修可明显缩短物资输送路径的通行时间,随着数据透明化和各相关部门联系紧密化,应该鼓励此种处理方式由理论走向实际,更大程度保证应急物资快速到达物资需求点。
在灾害前期通信能力受限的场景中,本文所提方法可以给应急部门提供参考方案,为快速恢复供电准备快速可靠的物资输送路径。

