新能源同步机对新能源多场站短路比的提升作用
杨 鑫, 黄永章, 2, 管 飞, 付文启, 武倩羽
(1.华北电力大学 电气与电子工程学院, 北京 102206;2.华电(烟台)功率半导体技术研究院有限公司, 山东 烟台 264006)
0 引 言
近年来,以太阳能和风能为代表的新能源成为可持续发展的重要解决方案[1,2]。据统计,2019年太阳能投资约为1 410亿美元,风能投资为1 430亿美元左右[3]。随着新能源发电占比逐渐增加,电网面临的电压稳定问题越发突出[4,5]。
短路比是衡量电力系统静态电压稳定性的重要指标,与系统电压支撑能力呈正相关[6]。系统短路比不足时,可能会引起电压不稳定、动态过电压和换流站不正常动态行为等问题,在直流换相失败故障后可能会引起功率振荡问题[7-9]。针对新能源电场,风机、光伏等通过电力电子变换器并网后,由于电力电子变换器的电流耐受能力低,故障时新能源电场能够提供的故障电流有限[10]。因此,新能源机组的大量安装会降低系统的短路比,危害系统安全。为提高系统短路比,文献[11,12]提出了一种电网自适应切换控制策略,该策略能够在电网电压跌落时,控制电压源换流器直流输电系统运行在纯无功输出模式,提高传统多直流输电馈入点的有效短路比。然而,改进控制策略基本不改变系统的短路容量,对短路比的提升有限。文献[13]分析得到STATCOM能够等效降低系统的临界短路比,提升直流输电系统的静态电压稳定性和运行极限。但STATCOM不提供短路电流,适用于电压突升或电压跌落较轻的场合[14]。文献[15]通过仿真分析了同步调相机对高压直流输电系统的短路比的提升效果。文献[16]提出了一种优化算法,用以确定同步调相机安装在以风电为主的电网中的最佳位置,从而增强系统强度。同步调相机本质上是空载的同步发电机,故障时能够向电网提供短路容量[17]。
同样基于同步电机理论,有学者提出了一种新型并网方式,新能源采用新能源同步机(motor-generator pair,MGP)并网,实验证明了该方式在提升新能源电网暂态稳定性、频率稳定性等方面能够发挥重要作用[18,19]。目前,尚未有研究分析MGP对系统静态电压稳定性的影响。因此,本文基于新能源多场站短路比(multiple renewable energy stations short-circuit ratio,MRSCR)的定义[20],研究MGP系统对系统静态电压稳定的提升作用。首先基于MGP结构分析了新能源采用MGP并网对短路容量的提升效果;然后,基于戴维南等值法和支路追加法分别分析了MGP对系统结构和网络阻抗矩阵的影响作用,从理论上说明了MGP对新能源多场站短路比的提升作用。最后在PSCAD仿真软件中搭建了新能源三场站系统的仿真模型,验证了MGP对MRSCR的提升作用,研究了MGP对暂态电压的抑制效果。
1 MGP并网系统
MGP由同轴连接的同步电动机和同步发电机组成。新能源经电力电子变换器输出电能,驱动MGP的电动机旋转,电能转换为机械能;再由机械轴驱动MGP的发电机并网发电,机械能转换为电能。结构如图1所示。

图1 MGP系统并网结构Fig. 1 Grid-connected structure of MGP
MGP的功率传输方程可表示为
(1)
式中:下标m、g分别表示电动机和发电机;P、δ分别为有功功率和功角;E、U分别为空载电动势和端电压;X为同步电抗;负号表示吸收有功功率。
由式(1)和同步电机基本理论可知,通过控制功角和电压能够实现MGP有功功率的实时控制和无功功率的灵活调节,其中功角由电力电子变换器控制,电压由MGP励磁系统控制。同步发电机运行时产生的损耗主要包括机械损耗,定子基本铜耗、励磁损耗等,以单台200 MW同步发电机为例[21],各项损耗如表1所示。
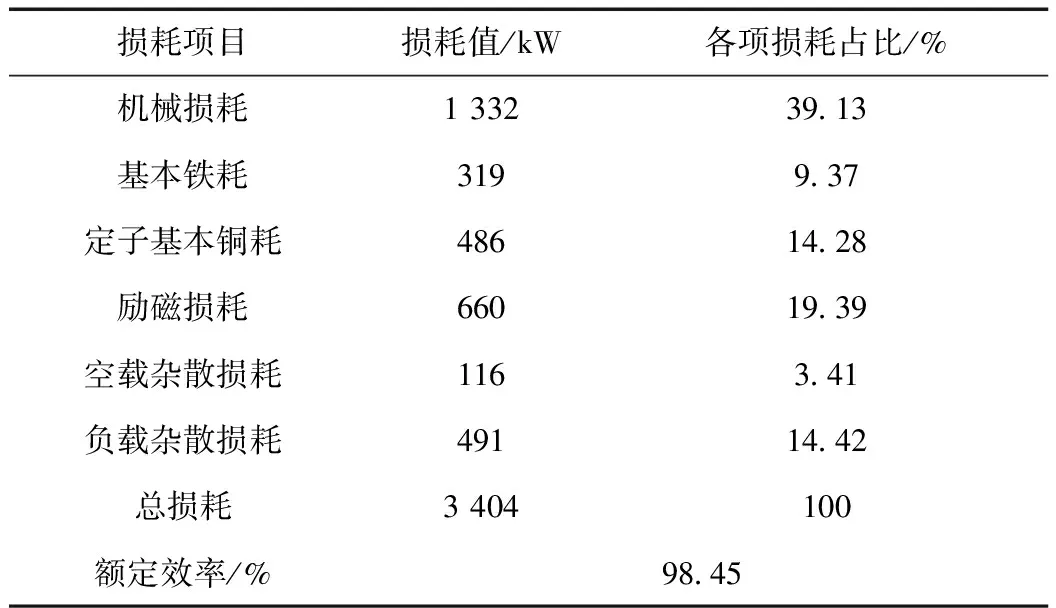
表1 200 MW同步发电机的损耗Tab.1 Loss of 200 MW synchronous generator
由表1可知,单台同步电机效率能够达到98%左右。MGP系统在两次能量转换过程中产生的损耗相当于两台同步电机的总损耗。因此,可以估计新能源采用MGP并网的效率为96%左右。考虑到新能源快速发展,被大量电力电子器件替代的同步电机可经改造后用于MGP,因此其成本是可接受的。
MGP作为当前电力电子并网方式的补充,能够为高比例新能源电力系统提供传统同步电机的优良属性,主要包括[21-23]:
(1)MGP真实的转子系统提供的机械转动惯量能够达到同容量火电机组的66%左右,可以有效改善系统的频率调节能力;
(2)MGP配置相应的励磁系统,可以提供足够的阻尼和电压支撑能力,从而抑制系统振荡,增强电网强度;
(3)MGP作为同步电机,能够承受1.3 p.u.甚至更高的暂态过电压,其机械轴能够有效阻断受端故障对源端的影响、源端故障对受端的影响以及谐波的影响。
因此,MGP为解决新能源电力系统日趋严重的频率和电压稳定问题提供了一个全新方案。文章主要研究MGP对电压稳定的影响,其它不再赘述。
2 MGP对MRSCR的提升作用
2.1 新能源多场站短路比
新能源多场站结构如图2所示,左侧为新能源场站,右侧为等值交流系统。参考直流多馈入短路比的定义,当系统满足以下3个条件时:
(1)新能源场站至电网的等值线路阻抗X/R>10;
(2)新能源各场站之间电压相角接近;
(3)并网节点电压相等。新能源多场站短路比定义为[20]
(2)
式中:MRSCRi为节点i的短路比;Saci和Ui分别为节点i的短路容量和电压;Peqi为考虑了其余新能源场站影响后的节点i的等值功率;Prei为第i个新能源场站的额定功率;Zeqij和Zeqii分别为交流网络侧的节点阻抗矩阵中对应节点的互阻抗和自阻抗。
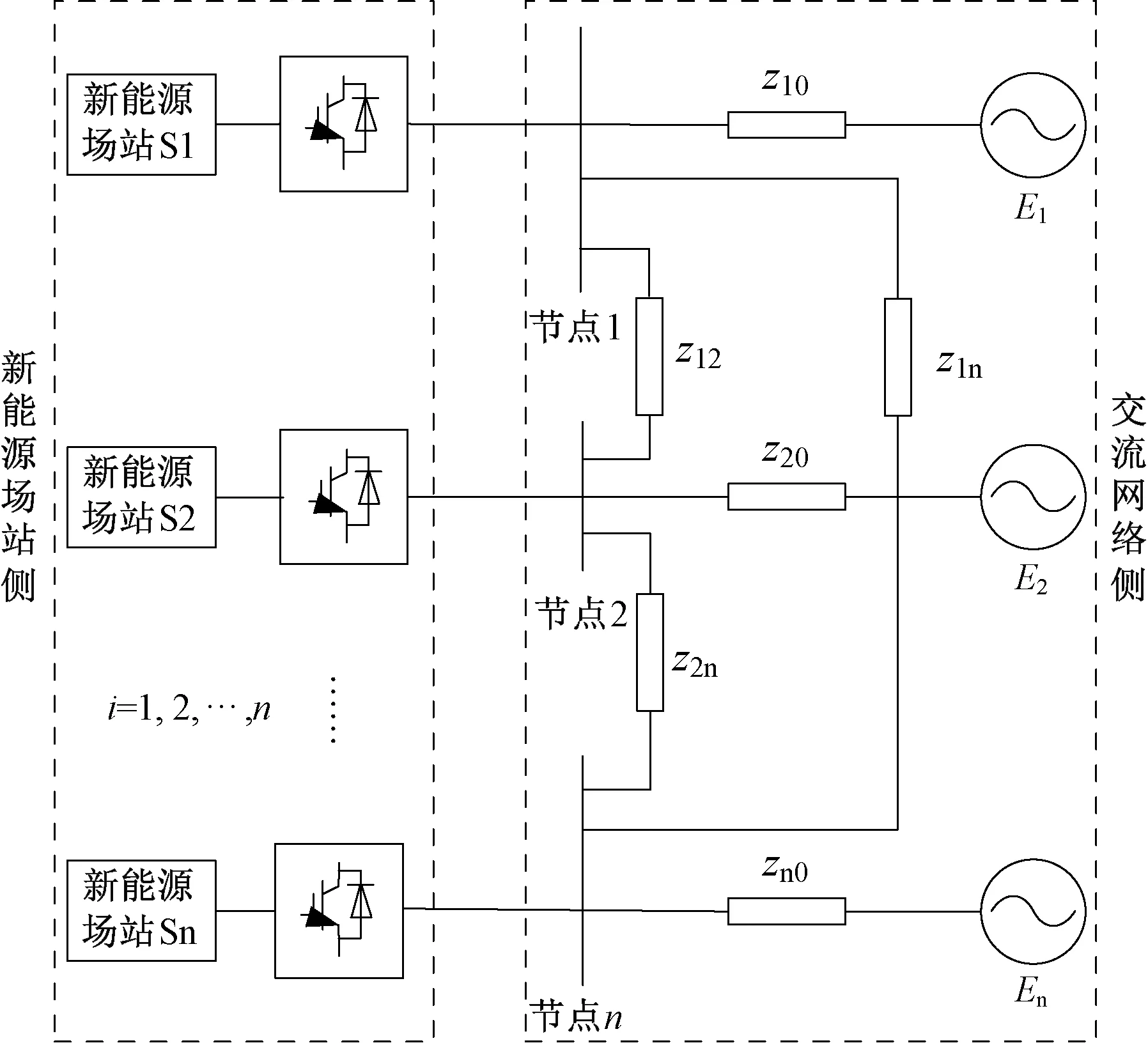
图2 新能源多场站结构Fig. 2 Structure of multiple renewable energy stations
以新能源并网节点的额定电压和第k个新能源场站额定容量分别作为基准电压值和基准功率值,则式(2)简化为
(3)
式中:Pi=Prei/Prek;Zij和Zii分别为Zeqij和Zeqii在基准值下的标幺值。
由上述定义可知,新能源多场站短路比反映了交流系统相较新能源发电容量的强弱程度,短路比越大,新能源对交流系统的影响越小,交流系统的支撑能力越强。
2.2 MGP对短路容量的提升作用
传统交流系统中的短路容量定义为
(4)
式中:Un为额定电压;Zeq为交流系统戴维南等值阻抗。
若已知短路点的故障电流,短路容量表示为
(5)
式中:ish为短路冲击电流,通常出现在短路发生的半个周期(0.01 s)左右;K为短路冲击系数,文中取1.9;Ik为短路电流的有效值。
由于MGP并网端的交流同步电机特性,新能源采用MGP并网后的整体可等效为传统电源,从而提升系统的短路容量。本节采用理论和仿真相结合的方式,在PSCAD仿真软件中搭建图3所示的仿真模型,分析MGP对短路容量的提升作用。主要参数如表2。仿真进行到10 s时,在A点设置三相短路故障,持续0.1 s,得到MGP发电机出口处的三相短路电流如图4所示。

图3 光伏采用MGP并网结构Fig. 3 Photovoltaic system adopts MGP grid connected structure
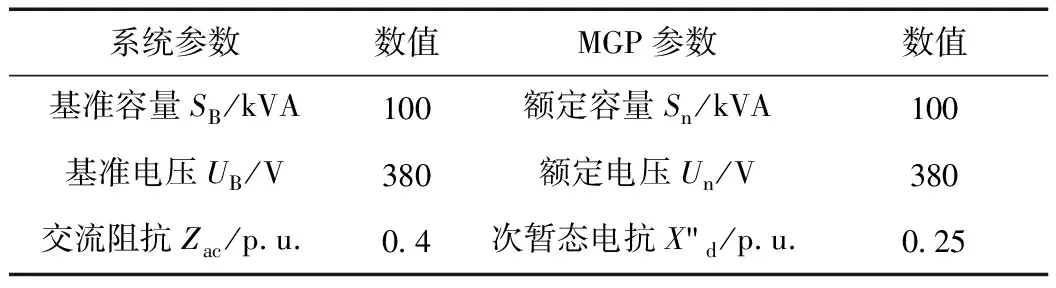
表2 主要参数Tab.2 Main parameters
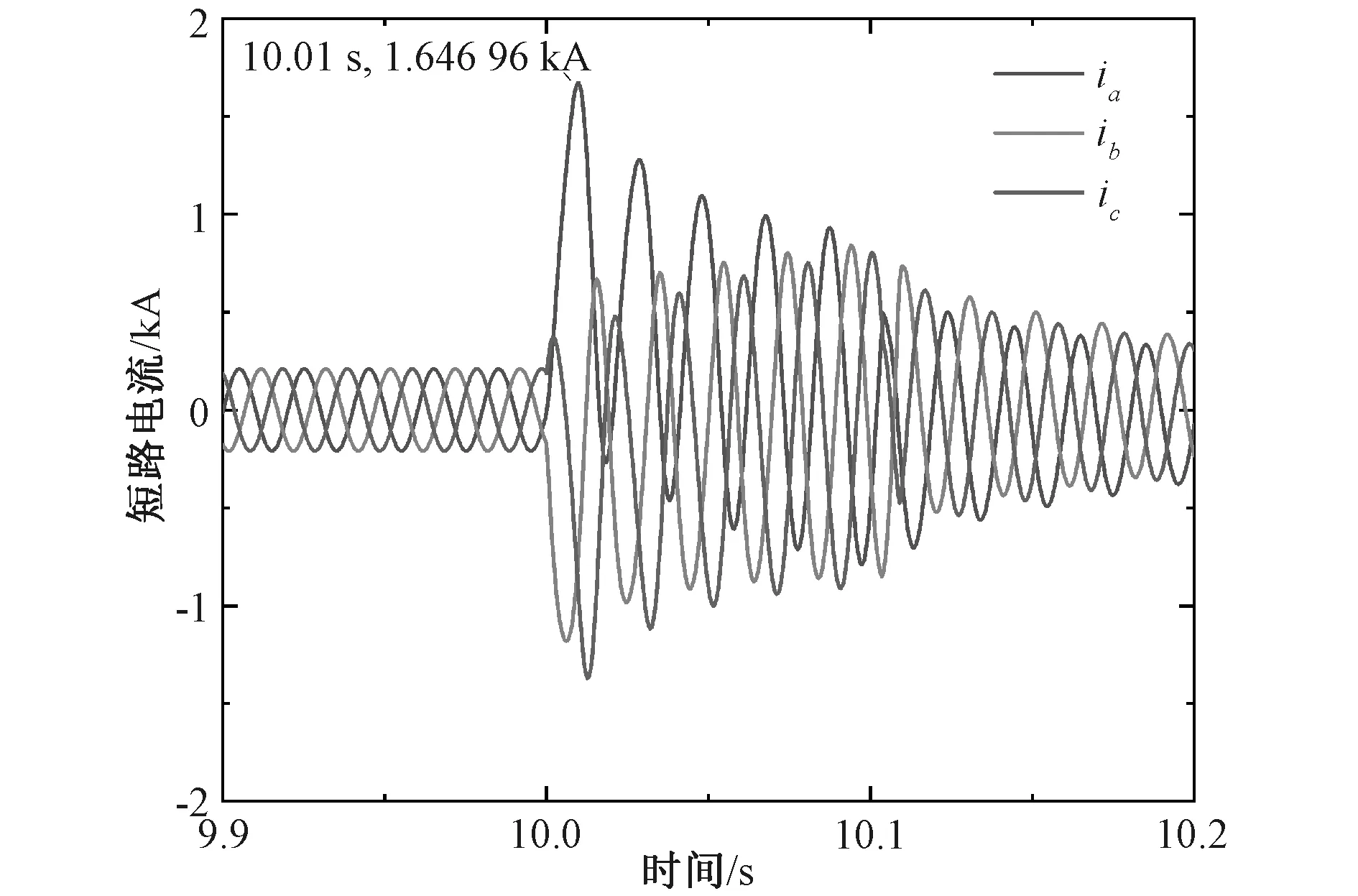
图4 MGP的三相短路电流Fig. 4 Three phase short circuit current of MGP
由图4可知,MGP发电机出口处的短路冲击电流约为1.647 kA。将仿真结果代入式(5),得到MGP提供的短路容量约为403.43 kVA。结合表2数据和式(4)计算得到MGP在A点提供的短路容量理论值为400 kVA。仿真结果与理论值的误差仅为0.86%,从而从短路容量的定义说明了新能源采用MGP并网后能够等效为传统电源,使新能源并网具备同步电机特性,向电力系统提供短路容量。
2.3 MGP提升新能源多场站短路比的机理
图2中新能源S1采用MGP并网的结构如图5所示。根据式(3)可知,MRSCR的大小与交流网络侧的节点阻抗矩阵的元素以及新能源场站的容量相关。基于上节分析结论,新能源采用MGP并网可等效为传统电源来提供短路容量。因此,MGP会改变新能源多场站系统的网架结构、影响交流网络参数,进而影响短路比。本节主要基于戴维南等值法和支路追加法具体分析MGP对新能源多场站短路比的影响。

图5 新能源场站S1经MGP并网结构Fig. 5 Structure of a renewable energy station via MGP grid-connected system
2.3.1 基于戴维南等值法分析MGP对系统结构的影响
戴维南等值方法可以简化电力网络计算,只考虑网络中多个端口与外电路之间的关系[24]。将整个网络的节点阻抗矩阵写成分块矩阵的形式:
(6)
式中:Zmm为需要研究的m个节点组成的m×m阶阻抗矩阵;Ztt为其余的t个节点组成的t×t阶阻抗矩阵;Zmt和Ztm为互阻抗矩阵。
上式中Zmm即为m端口的戴维南等值节点阻抗矩阵。设图5所示系统的节点阻抗矩阵为
(7)
式中:下标1、n-1、n等为矩阵的阶数;Zn×n为n个节点组成的交流网络侧节点阻抗矩阵;Z1×1为节点1的自阻抗矩阵;Z(n-1)×(n-1)为除节点1外,其余n-1个节点组成的节点阻抗矩阵;Z1×(n-1)和Z(n-1)×1分别为对应节点的互阻抗矩阵。
新能源S1采用MGP并网等效为传统电源后,节点1左侧为传统电源,右侧为交流系统,故节点1的短路比可不作考虑,同时对其余n-1个新能源直接并网的节点进行戴维南等值,得到n-1端口的交流网络侧节点阻抗矩阵为Z(n-1)×(n-1)。因此,图5所示系统的新能源多场站短路比计算公式为
(8)
式中:MRSCRu为节点u的短路比,u1;Sacu和Uu分别为节点u的短路容量和电压;Pequ为考虑了其余新能源场站影响后的节点u的等值功率;Preu为第u个新能源场站的额定功率;Zequv和Zequu分别为Z(n-1)×(n-1)中对应节点的互阻抗和自阻抗。
以新能源并网节点的额定电压和第k个新能源场站额定容量分别作为基准电压值和基准功率值,则式(8)简化为
(9)
式中:Pu=Preu/Prek;Zuv和Zuu分别为Zequv和Zequu在基准值下的标幺值;u1。
根据上式可知,式(9)分母为∣Zuu∣Pu和n-2项∣Zuv∣Pv相加,相较式(3)减少了一项,不再考虑新能源S1发电容量对短路比的影响。由于采用MGP并网的新能源具备了同步电机特性,原来削弱交流电网强度的新能源S1因此具备了提供短路容量的能力,改变了新能源n场站系统的结构和交流电网相对新能源的强弱程度。影响程度与新能源采用MGP并网容量以及结构变化导致的阻抗矩阵变化有关。
2.3.2 基于支路追加法分析MGP对节点阻抗矩阵影响
支路追加法能够在部分网络的基础上不断叠加新的支路,最终形成整个网络的节点阻抗矩阵,可以反映结构变化导致的阻抗变化过程[25]。本小节以图2和图5所示结构为例,基于支路追加法原理分析MGP对节点阻抗矩阵的影响。
新能源S1采用MGP并网等效为传统电源后,外特性表现为电压源,原新能源n场站系统的交流网络侧(以下简称原系统)由此增加了一条支路,阻抗为zmgp,如图6所示。图中节点1、2、……、n为并网节点,节点0为参考节点。

图6 支路阻抗简化图Fig. 6 Simplified diagram of branch impedance
由支路追加法原理可得,图5系统交流网络侧(以下简称新系统)的n×n阶节点阻抗矩阵计算公式如下:
(10)
(11)
式中:Z和Z0分别为新系统和原系统节点阻抗矩阵,阶数均为n×n;A0为原系统的节点支路关联矩阵;Mmgp为支路zmgp本身的节点支路关联矢量,文中Mmgp=[1 … 0 … 0];zmgp为MGP到节点1线路阻抗与其发电机次暂态电抗X"d的和值;z0为原系统的支路阻抗矩阵;支路zmgp与原系统之间无耦合,即zmgp0=0,z0mgp=0T,c1,c2为零矢量。
结合式(10)和式(11)得
(12)
设原系统的线路参数均为纯感性,根据支路追加法原理迭代可得Z0中元素均为纯感性,即Z0与zmgp同号。进一步由式(12)可知,Z 综上,对比式(9)相较式(3)各量变化可知,MRSCRu>MRSCRi(u=i,且u1时),即MGP提升了新能源多场站短路比。 本节采用理论计算和仿真分析相结合的方式,通过具体算例验证2.3节的理论。 基于图2和图5所示结构设置新能源三场站算例(n=3)。设系统基准容量为100 kVA,基准电压为380 V。算例中的主要参数如表3所示,线路主要参数如表4所示。 表3 新能源三场站参数Tab.3 Parameters of three renewable energy stations 表4 线路参数Tab.4 Line parameters 计算步骤为: (1)根据表4计算原系统三阶节点阻抗矩阵Z0,如式(13); (2)不计MGP到并网节点1的线路阻抗,即zmgp=X"d=0.22。将Mmgp=[1 0 0],zmgp和Z0代入式(12),得到新系统三阶节点阻抗矩阵Z,如式(14); (3)根据戴维南等值原理得到新系统二阶节点阻抗矩阵Z2×2。结合表3数据,分别将Z0代入式(3),Z2×2代入式(9),得到无/有新能源采用MGP并网时,新能源多场站短路比的理论值如表5。 (13) (14) 表5 新能源多场站短路比理论值Tab.5 Theoretical results of MRSCR 对比式(13)和式(14)可知,Z 在PSCAD仿真软件中搭建图2和图5所示的新能源三场站仿真模型(n=3),仿真参数同3.1节。仿真进行到10 s时,分别在节点1、2、3设定三相短路故障,持续0.1 s后清除,得到各节点的单相短路电流如图7所示。 图7 短路电流的仿真结果Fig. 7 Simulation results of short circuit current 仿真测量的电流位于节点1、2、3至短接点之间,短接点设置在新能源三场站系统之外,因此短路前和故障清除后的电流基本为零。根据图7(a)和(b)可知,MGP向系统提供了额外的短路电流,其中无新能源采用MGP并网时,各节点短路冲击电流约为3.017 kA,4.665 kA,2.853 kA;新能源S1采用MGP并网时,各节点短路冲击电流约为4.481 kA,5.211 kA,3.289 kA。将仿真结果及新能源容量、阻抗等参数依次代入式(5)、式(2)和式(5)、式(8),分别得到无/有新能源采用MGP并网时,新能源多场站短路比的仿真计算值如表6所示。 表6 新能源多场站短路比仿真值Tab.6 Simulation results of MRSCR 对比表5和表6可知,仿真结果与理论值接近,两者均验证了MGP对新能源多场站短路比的提升作用。文中为便于分析,选择新能源多场站直接并网和仅新能源S1采用MGP并网两种结构作为对照组,其结论也适用于新能源S2或S3采用MGP并网等不同结构。不同结构对短路比影响程度有所区别,主要受MGP并网容量、接入位置、发电机次暂态电抗以及MGP至并网点线路阻抗等因素影响。 短路比能够反映系统强度,短路比越大,静态电压稳定性越好,系统抑制暂态电压的能力越强。为分析MGP对系统电压稳定性的提升作用,本节基于前文的仿真模型,研究MGP对暂态电压的抑制效果。分别在节点2和节点3设置三相短路故障,持续0.1 s后清除故障,得到无/有新能源采用MGP并网时三个节点的电压变化如图8所示。图中虚线为新能源不采用MGP并网时的各节点电压,实线为新能源S1采用MGP并网时的各节点电压。 由图8(a)可知,节点2短路时,系统各节点电压开始跌落,在10.1 s左右跌至最低值。其中,采用MGP并网方式的新能源三场站系统可以抑制暂态低电压,节点1和节点3电压跌落的幅值均低于不采用MGP并网的新能源三场站系统;由于短路发生在节点2,测量电压为节点电压,故U2均趋于0。故障清除后,各节点电压由低电压恢复至稳态的过程中均出现了暂态过电压,采用MGP并网方式能够抑制各节点暂态过电压的升高。由图8 (b)可知,节点3短路时,MGP也能够抑制暂态低电压和暂态过电压。 图8 暂态电压的仿真结果Fig. 8 Simulation results of transient voltage 综上,采用MGP并网方式能够有效提升新能源多场站系统短路比水平,增强系统强度,提升系统静态电压稳定性,抑制故障过程中的暂态电压。 文章基于戴维南等值方法和支路追加法,分析了MGP对新能源多场站短路比的提升作用。得到如下结论: (1)MGP并网方式能够使新能源并网具备同步电机特性,像传统电源一样提供短路容量,改变了新能源n场站系统结构,缩短了源网电气距离。 (2)通过理论计算和仿真分析,验证了采用MGP并网方式能够提升新能源多场站短路比,增强系统强度,抑制暂态电压。 文章的研究忽略了输电线路的电阻特性。在复杂网络参数下,分析MGP对新能源多场站短路比的影响,并与同步调相机进行比较是下一步的研究重点。3 MGP提升MRSCR的算例验证
3.1 理论计算
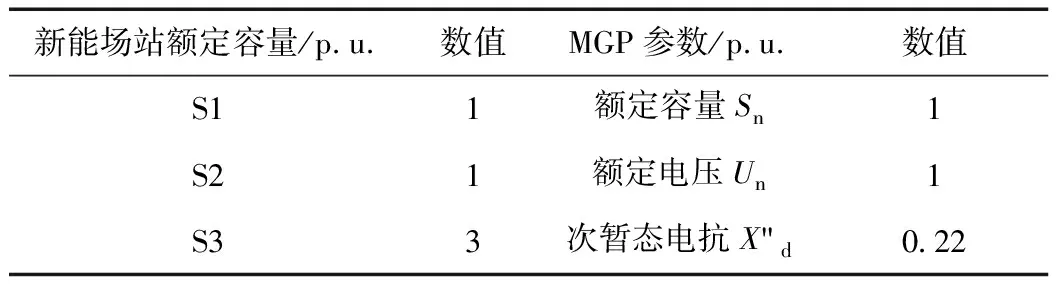
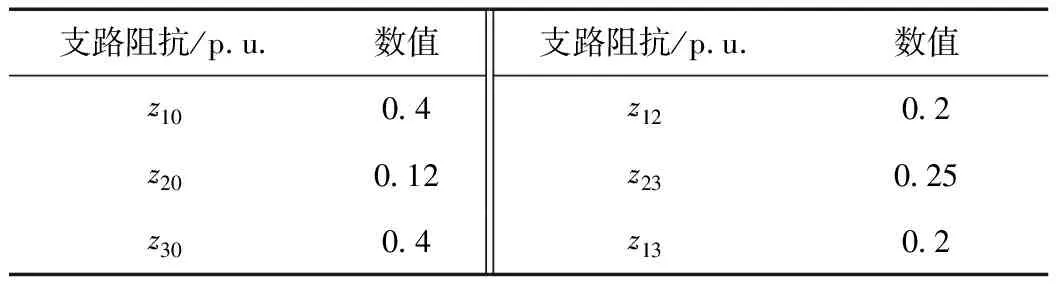


3.2 仿真验证


4 MGP对暂态电压的抑制作用
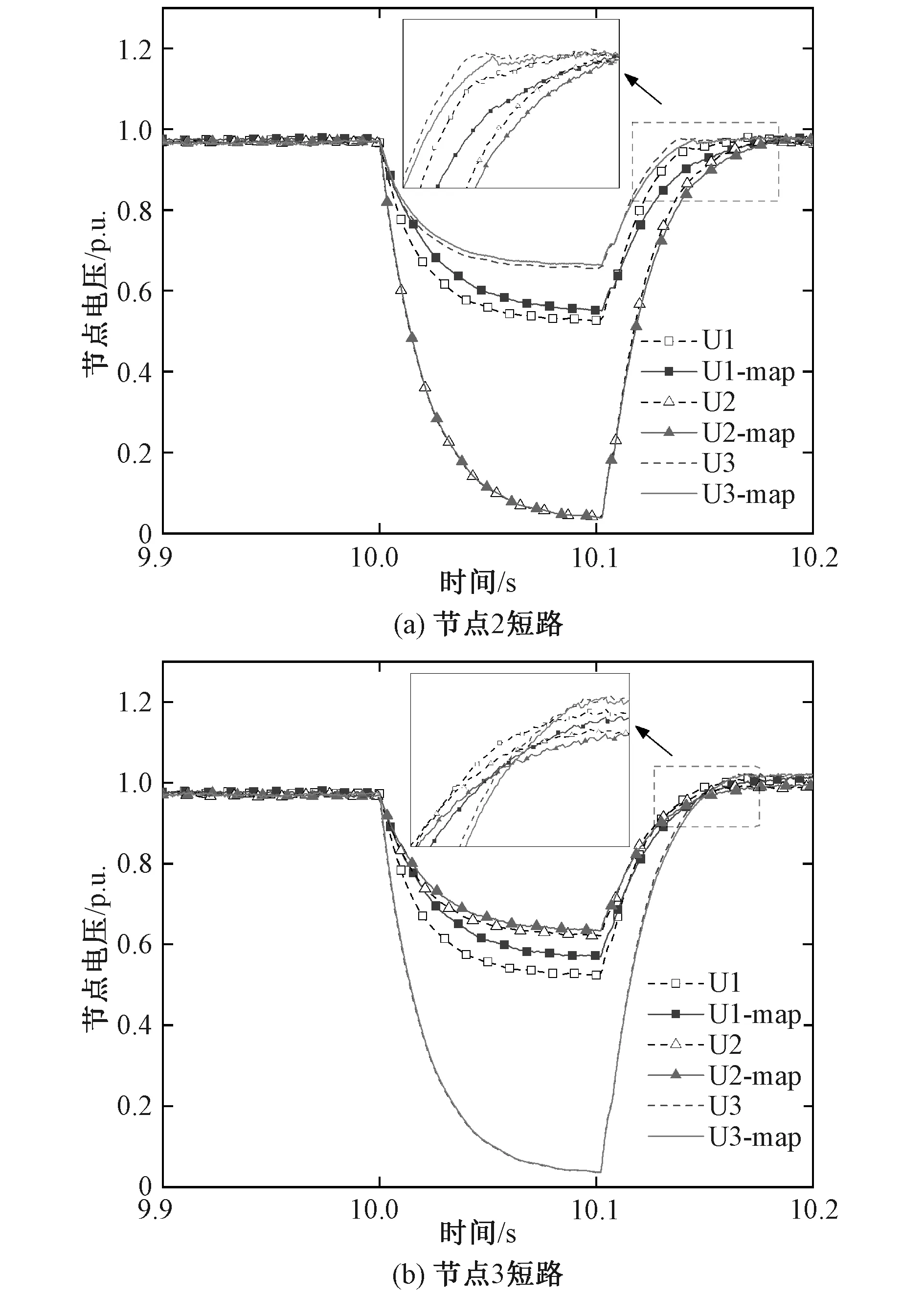
5 结 论

