UCM冷轧机弯辊力智能预设定计算模型研究

金 鑫，李 萍，高军霞，苑少强

(唐山学院 机电工程学院，河北省智能装备数字化设计及过程仿真重点实验室，河北 唐山 063000)

0 引言

冷轧带钢具有尺寸精度高、钢体表面质量好和易于加工等特点，被广泛应用于汽车、家电、建筑、包装等各个领域[1-3]。随着下游工序对尺寸精度要求的不断提高，冷轧带钢的板形质量已成为其品质提升的瓶颈[4-5]。六辊UCM(Universal Crown Mill)冷轧机配置有工作辊弯辊、中间辊弯辊和中间辊横移等多种板形执行机构，已成为生产冷轧带钢的主要机型。

在一卷带钢咬入冷轧机之前，冷轧机组的板形控制系统会根据来料与成品规格、轧辊直径、带钢材质等主要参数对弯辊力进行预设定计算，以保证带钢头、尾部的平直度，因此，预设定计算精度是保证带钢品质和成材率的关键[6-8]。为了提升弯辊力预设定模型的计算精度，一些学者和工程技术人员做了大量研究，并取得了一定成果。早期的弯辊力预设定模型计算主要采用解析法，计算过程假设较多，影响计算精度[9]。随着计算机技术的不断发展，有限元法逐渐被用于预设定模型的开发[10-13]，但受制于计算速度，并不适合在线应用。影响函数法计算速度快、计算精度较高，用其开发的模型适合在线应用，易于与各种智能算法相结合解决轧制过程中的板形优化问题，是目前使用较为广泛的计算方法[14-15]。

但已有研究只是针对单一弯辊机构的预设定模型，关于工作辊和中间辊如何协调优化的问题目前尚缺乏系统的研究。因此，本文基于影响函数法建立冷轧带钢板形计算模型，并与基本遗传算法相结合，建立弯辊力预设定模型，进而确定工作辊弯辊力和中间辊弯辊力的最优匹配值，为冷轧机组板形控制系统优化提供理论指导与技术支持。

1 板形计算模型

1.1 变形抗力模型和轧制力模型

变形抗力模型精度直接影响轧制力和辊间压力的计算精度，进而决定辊系弹性变形计算和板形预测精度。因此，建立高精度变形抗力模型是提升板形预测精度的基础[16]。

本研究采用轧制-拉伸法建立轧制过程变形抗力模型。热轧板经由实验冷轧机轧制成不同厚度的冷轧板，然后对冷轧板进行室温拉伸实验，测得不同压下率冷轧板的屈服强度，再利用Origin软件回归得到实验钢的变形抗力模型，模型结构如式(1)所示：

K=K0+εa(b-K0)。

(1)

式中，K为材料的变形抗力，MPa；a，b和K0为模型待定参数；ε为道次累积真应变，由式(2)计算得到：

(2)

式中，r为道次累积压下率，是由热轧带钢轧至本道次时所有道次的累积变形，如式(3)所示：

r=(1-β)rb+βrf。

(3)

式中，β为系数，一般取0.75；rb，rf分别为道次入口压下率和道次出口压下率，如式(4)和式(5)所示：

(4)

(5)

式中，h0为热轧带钢厚度，mm；hentry为道次入口带钢厚度，mm；hexit为道次出口带钢厚度，mm。通过式(1)-(5)计算得到材料变形抗力后，采用Bland-Ford-Hill方程计算轧制力，如式(6)所示：

(6)

式中，P为轧制力，N；B为带钢宽度，mm；QP为外摩擦影响系数；KT为张力影响因子；R′为工作辊压扁半径，mm。

式(6)中QP的计算方法如式(7)：

(7)

KT的计算方法如式(8)：

(8)

式中，τf与τb分别为道次的前、后张力，MPa。

工作辊压扁半径的计算方法如式(9)：

(9)

式中，R为工作辊半径，mm；CH为Hitchcock系数，计算方法如式(10)所示：

(10)

式中，υS为带钢的泊松比；ES为带钢的弹性模量，MPa。

1.2 辊系弹性变形模型

影响函数法通过将带钢、轧辊以及轧辊所受的力离散化，求出轧辊横向各位置的弹性挠曲与弹性压扁，进而确定带钢板形。基于影响函数法，建立辊系弹性变形模型，轧辊、轧辊受力和带钢均被离散为若干单元。每个单元的受力根据轧制力分布计算得到，则i单元受各单元力影响下的总变形y(i)按照式(11)进行计算：

(11)

式中，i，j为轧辊横向单元；P(j)为j单元的单位轧制力，由材料强度和带钢入口、出口厚度确定；g(i，j)为j单元受力对i单元的影响函数。

轧辊弯曲影响函数gr(i，j)如式(12)和(13)所示：

(12)

(13)

式中，Er为轧辊的弹性模量，MPa；Wr为轧辊的抗弯截面系数，mm4；vr为轧辊泊松比；xi和xj为轧辊单元坐标，mm；Dr为轧辊直径，mm。

弯辊力影响函数gf(i)如式(14)所示：

vr)Dr2xi]。

(14)

式中，Lr为两侧弯辊液压缸之间的距离，mm。

由轧制力引起的轧辊压扁影响函数gws(i，j)如式(15)所示：

gws(i，j)=Φ(a)+Φ(b)。

(15)

式中，a=xi+xj，b=xi-xj。Φ(a)如式(16)所示，Φ(b)如式(17)所示：

Φ(a)=

(16)

Φ(b)=

(17)

式中，Δx为i单元与j单元的距离，mm；l为变形区接触弧长，mm。

辊系弹性变形计算流程如图1所示。

图1 辊系弹性变形计算流程

1.3 带钢轧后板形计算模型

为了保证板形良好，轧前、轧后带钢凸度必须成比例减少，即需要满足式(18)：

(18)

(19)

式中，α，β，γ为与材料有关的系数。

辊缝和带钢形状的失配会导致入口和出口带钢比例凸度发生变化，进而引起横向延伸的不均匀。轧后带钢板形定义如式(20)所示：

(20)

忽略冷轧过程引起的带钢宽度变化，根据体积不变原理，可得到式(21)：

H(i)L(i)=h(i)l(i)。

(21)

式中，H(i)与L(i)为i单元带钢入口厚度和长度，mm；h(i)与l(i)为i单元带钢出口厚度和长度，mm。

式(21)两边取增量，可得式(22)：

[H(i)+ΔH(i)][L(i)+ΔL(i)]=[h(i)+Δh(i)][l(i)+Δl(i)]。

(22)

展开式(22)，可得式(23)：

H(i)L(i)+H(i)ΔL(i)+L(i)ΔH(i)+ΔH(i)ΔL(i)=h(i)l(i)+h(i)Δl(i)+l(i)Δh(i)+Δh(i)Δl(i)。

(23)

式(23)除以式(21)，可得式(24)：

(24)

(25)

2 弯辊力预设定模型

为了确定UCM冷轧机工作辊弯辊力和中间辊弯辊力的最佳匹配值，需要将开发的板形计算模型嵌入基本遗传算法中，建立弯辊力智能预设定模型。下面介绍基本遗传算法的计算步骤、改进的适应度函数、边界条件以及弯辊力预设定模型的计算步骤。

2.1 基本遗传算法

基本遗传算法是一种全局优化计算方法，具有很强的泛化性，能够有效地解决复杂问题，并已成功应用于轧制领域[17-18]。基本遗传算法的一般步骤如下：

(1)初始化种群，设定一组随机输入值；

(2)计算种群中所有个体的解作为适应度值，并对其进行评价；

(3)判断当前解或遗传代数是否满足要求，如果是，转向步骤(6)，如果不是，转向步骤(4)；

(4)根据步骤(2)对适应度的评价结果，从当前解中选择部分解进入基本遗传操作；

(5)对选出的解进行交叉、变异操作，生成一组新解，转向步骤(2)；

(6)输出当前最优解。

在以上步骤中，所有操作过程均为随机处理，基本遗传算法的计算流程如图2所示。

图2 基本遗传算法的计算流程

2.2 适应度函数

一直以来，为了改善板形质量，始终将保持各道次出口带钢比例凸度不变作为目标函数，如式(26)所示：

(26)

式中，Δk为允许的比例凸度允许变化量，mm。

这种目标函数计算速度快，但适用条件有限。当来料存在板形缺陷、强度波动等问题时，此目标函数会将缺陷向下游道次遗传，致使板形优化的目的难以达到。因此，目标函数中不能只考虑带钢比例凸度。相比于比例凸度，带钢的轧后平直度可以更直观地反映带钢板形质量。基于前文建立的板形计算模型，应将轧后带钢平直度计算值作为目标函数，基本遗传算法的适应度函数Fitness可表示为：

(27)

式中，C为带钢轧后平直度，IU，平直度越小代表板形质量越好。在基本遗传算法中，遗传操作将适应度小的解淘汰，而适应度大的解则被保留至下一代，所以适应度函数需要进行倒数处理。C按式(28)计算：

。

(28)

式中，n为带钢单元数量，z=1，2，…，n；flatnessz为带钢第z单元的平直度，IU。

2.3 边界条件

在设定计算过程中，弯辊力的设定值不能超过设备极限，弯辊力的边界条件按照式(29)定义：

(29)

式中，WRB和IRB分别为工作辊弯辊力和中间辊弯辊力的设定值，kN；WRBmax和IRBmax分别为工作辊弯辊力和中间辊弯辊力的允许最大值，kN。同时，轧制力、轧制力矩和轧制功率也不能超过设备的工艺极限。因此，边界条件还需包含：

(30)

式中，P，PW和T分别为轧制力、轧制功率和轧制力矩的计算值；Pmax，PWmax和Tmax分别为轧制力、轧制功率和轧制力矩的允许最大值。

2.4 模型计算步骤

基于前文改进的适应度函数和边界条件，弯辊力智能预设定模型的计算步骤如下：

(1)随机生成一组满足边界条件的工作辊弯辊力和中间辊弯辊力；

(2)调用开发的板形计算模型，计算轧后带钢平直度C；

(3)根据适应度函数评价染色体，选择最优个体进入基本遗传操作；

(4)开始遗传迭代计算，经过选择、交叉、变异操作后，再次调用板形计算模型计算轧后带钢平直度并进行染色体评价，同时保留最优个体；

(5)如迭代计算次数满足进化代数或精度已达标，此时输出最优工作辊和中间辊弯辊力，否则返回步骤(2)。

弯辊力智能预设定模型的计算流程如图3所示。

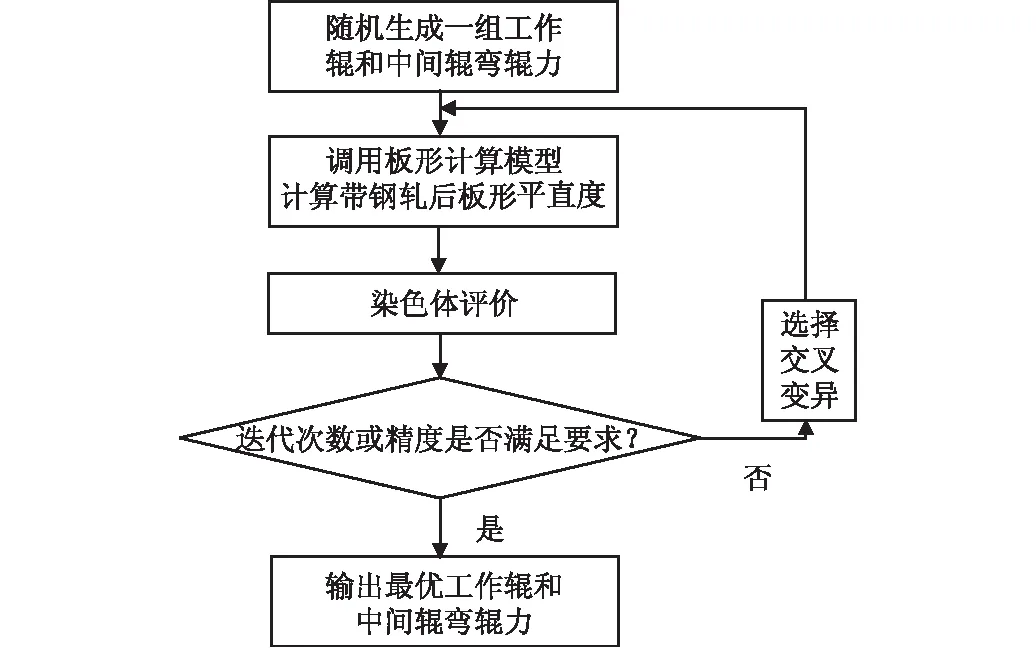
图3 弯辊力智能预设定模型计算流程

3 弯辊力智能预设定模型计算结果

基于前文的研究结果，根据某六辊UCM冷轧机的设备和材料参数对弯辊力进行预设定计算，设备和材料参数如表1所示。带钢宽度1 250 mm，轧前厚度3.5 mm，轧后厚度2.1 mm。遗传算法的种群规模设为50，进化代数设为100，交叉率和变异率分别为0.9和0.1。图4为预设定计算结果，其中适应度值随遗传代数的变化如图4(a)所示，弯辊力设定值随遗传代数的变化如图4(b)所示。

表1 预设定计算相关设备及材料参数

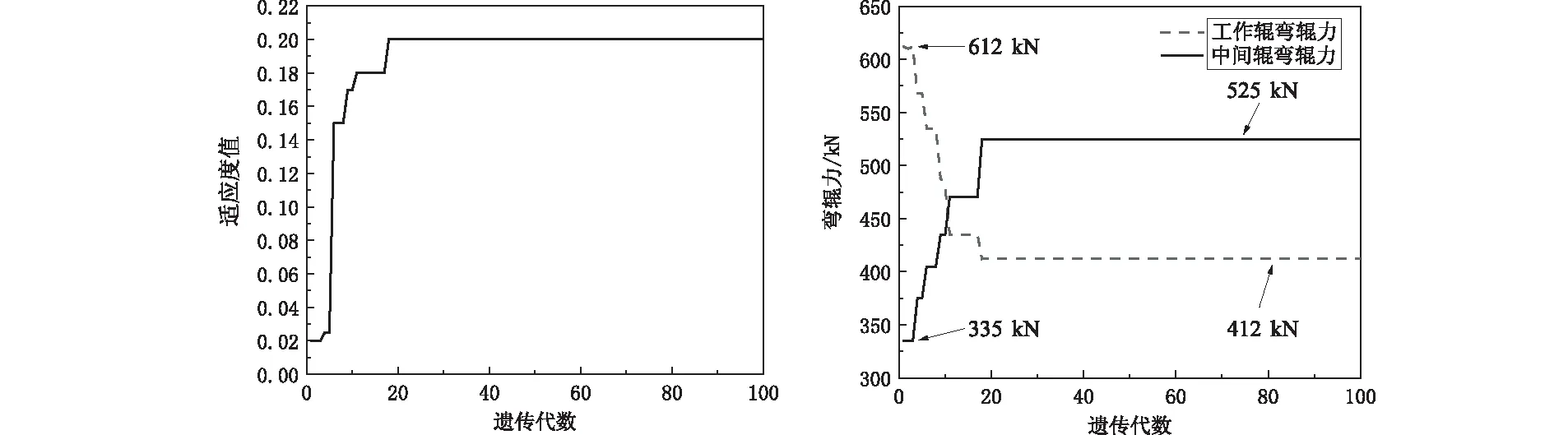
(a)适应度随遗传代数的变化 (b)工作辊和中间辊弯辊力随遗传代数的变化图4 弯辊力预设定计算结果

由图4(a)可知，遗传算法的求解过程在18代之后收敛。如图4(b)所示，在求解过程中，工作辊弯辊力由612 kN降至412 kN，中间辊弯辊力由335 kN升至525 kN。为进一步探究求解过程中弯辊力呈此规律变化的原因，将轧后板形与遗传代数的数据提取出来，如图5所示。

图5 轧后带钢板形计算值与遗传代数的关系

由图5可知，初始的工作辊弯辊力较高，带钢呈现比较明显的中浪。随着工作辊弯辊力的降低，带钢板形由中浪转变为肋浪与边浪共存的复合浪形。此时工作辊弯辊力继续降低，中间辊弯辊力适当增加，有效地缓解了肋浪缺陷，带钢板形趋于平直，板形峰值降低至10 IU以内。由此可见，在适当降低工作辊弯辊力的同时增加中间辊弯辊力是有效缓解轧后带钢板形肋浪缺陷的方法之一。

4 结论

(1)建立了六辊UCM冷轧机板形计算模型，通过该模型输入轧制过程工艺参数，可以计算得到辊间接触压力、轧辊弹性变形和带钢轧后板形。

(2)使用带钢轧后平直度的倒数作为适应度函数，将开发的板形计算模型与遗传算法相结合，建立了弯辊力智能预设定计算模型，并使用该模型对SPHC带钢弯辊力进行了预设定计算。遗传算法的计算过程在18代之后收敛，最终确定最优的工作辊和中间辊弯辊力分别为412 kN和525 kN。

(3)随着工作辊弯辊力的降低和中间辊弯辊力的增加，轧后带钢板形最终由中浪转变为肋浪，最后趋于平直，板形峰值低于10 IU。