基于改进NSGA-III的医疗器械产品配置优化设计研究

郭 晨,李庞聪,王 磊

(1 武汉理工大学 安全科学与应急管理学院,湖北 武汉 430070;2．武汉理工大学 机电工程学院,湖北 武汉 430070)

近年来，国内外学者针对产品配置问题展开了大量的研究。张雷[1]等将绿色产品需求转化为配置约束，并在回溯算法中加入约束过滤模块与建议性约束满足模块，求解豆浆机的配置方案。Dong等[2]通过将结构化产品的结构知识转化为动态约束配置里的编码，减小了DCSP(distributed constraint optimization problem)中编码变量的数量，并采用回溯搜索求得最优解。赵燕伟等[3]提出根据不同的局部相似度类型，为实例动态赋权的可拓展相似度计算方法，并结合客户偏好计算配置方案总体相似度。肖刚等[4]提出了一种加权欧式距离计算方法求解待配置产品与历史实例的相似性。Wang等[5]提出了一种基于灰度粗糙模型的客户需求分析方法，将不确定的客户需求转化为确定的产品技术特征及技术特征重要度，采用了一种无监督的自学习神经网络技术-自组织映射方法(self-organizing map, SOM)对案例库中的案例进行聚类以缩小检索范围，提出了一种基于模糊相似度优先比的相似度度量方法来获取相似的案例。Wei等[6]以性能、成本、时间为目标对产品进行配置，采用NSGA-II(non-dominated sorted genetic algorithm-II)算法求解配置方案，提出了一种基于模糊度的配置方案评估与选择机制在Pareto前沿中选择最优方案。Tang等[7]建立了一种同时考虑用户满意度与产品全生命周期碳排放的模型，并采用遗传算法求解最优配置方案。

笔者在传统产品配置的研究目标上，考虑医疗器械生产过程中，回料对产品可靠性与成本的影响，建立了精密过滤输液器产品配置优化模型。针对本模型决策变量空间与解空间过大的问题，提出了一种改进NSGA-III算法，增加了种群混沌映射初始化与局部搜索算子，改善了NSGA-III算法在局部搜索能力上的不足。最后，结合某医疗器械企业的产品实际案例，通过与NSGA-III算法、CS(cuckoo search)算法、Pareto-IMODCS(pareto-inproved multiple-objective discrete cu ckoo search)算法进行对比，证明了改进NSGA-III的可行性与优越性。

1 问题描述及数学模型

1.1 问题描述

输液器在部件的生产过程中，不可避免地会生产出带有污点、外观变形等不合格缺陷的部件。不合格的部件经过质检筛选后，部分会重新粉碎成塑料原料(经过重新粉碎的塑料原料定义为回料)。研究表明，回料过程中的后处理会引起ABS中的聚丁二烯断裂，降低回料与原料混合后的冲击强度[8]、抗拉强度、抗扭强度[9]等机械性能，造成零部件可靠性下降。生产实践的统计数据显示，零部件的可靠性随回料增加呈线性降低的趋势。精密过滤输液器任意模块的失效都将导致产品整体的失效，因此精密过滤输液器是一个串联系统。串联系统的模型如图1所示。

图1 串联系统模型可靠性框图[10]

(1)

式中：Rt为配置方案可靠性；n为模块数量；ni为第i个模块的实例数量；bij为0-1整数变量，表示第i个模块的第j个实例是否被选中参与配置；R(mij)为实例mij的可靠性。

R(mij)=Rij-αij·rij

(2)

式中：αij为常数，表示回料比例与实例可靠性之间的相关性；Rij为第i个模块的第j个实例在不使用回料情况下的可靠性；rij第i个模块的第j个实例的回料比例。

1.2 数学模型

配置方案的总成本优化数学模型为：

pW(mij)(1+rij(θ-1)))

(3)

式中：Ct为配置方案的总成本；W(mij)为第i个模块的第j个实例需要的原材料数量；p为原材料单位价格；Cz(mij)为第i个模块的第j个实例的制造成本；θ为配置方案中使用回料时计算成本的折扣比例。

式(3)表示配置方案总成本，应尽可能小。总成本由配置方案的材料成本和除材料以外的所有制造成本构成，其中θ为经验值，由设计人员与财务人员分析和归纳历史数据后确定。

配置方案的总生产时间应尽可能短，其优化教学模型为：

(4)

式中：T(mij)为第i个模块的第j个实例的生产时间；Tt为方案总生产时间。

配置方案的可靠性在实际生产中应尽可能高。配置方案的可靠性优化模型为：

(5)

1.3 约束处理

为了便于计算，统一所有目标函数为最小值。将最大化可靠性目标函数做取反处理，得到对应的最小化可靠性函数minNRt=-Rt。

模型的不等式约束如下：

F(xi)={minCt,minTt,minNRt}

g1≤0

g2=RSd+RSr

(6)

式中：xi=[xi1,xi2,…,xin]为配置问题的一个解，n为产品的模块数量；g1为成本、原材料等约束；g2为配置方案的实例依赖约束和排斥约束的总违反次数，g2=0时表示配置方案满足实例依赖排斥约束，g2值越大表示配置方案在该约束上的违反程度越大；RSd为实例间的依赖约束，RSr为实例间的排斥约束。

采用惩罚函数法与多目标优化法相结合的混合方法，以惩罚函数作为当前解对约束条件违反程度的度量，将其作为第四维目标函数求解最小值。个体违反约束条件程度的度量函数定义如下：

(7)

(8)

式中：cj=max(0,gj(x)),j=1,2,…,k。

显然，约束违反度越低，表示配置方案对约束的满足程度越高，CV=0的配置方案没有违反任何约束，为完全可行方案。此时，式(6)中的目标函数F(x)可转化为：

F1(xi)={minCt,minTt,minNRt,minCV}

(9)

2 算法求解

2.1 产品配置方案染色体的表示

产品配置方案以一段整数编码的染色体表示。染色体信息由两部分构成，前半部分代表可配置模块，基因值的取值范围由可配置实例的索引值组成。染色体信息的后半部分代表染色体前半部分选中的模块实例在生产中使用的回料比例。产品配置方案的基因编码如图2所示。

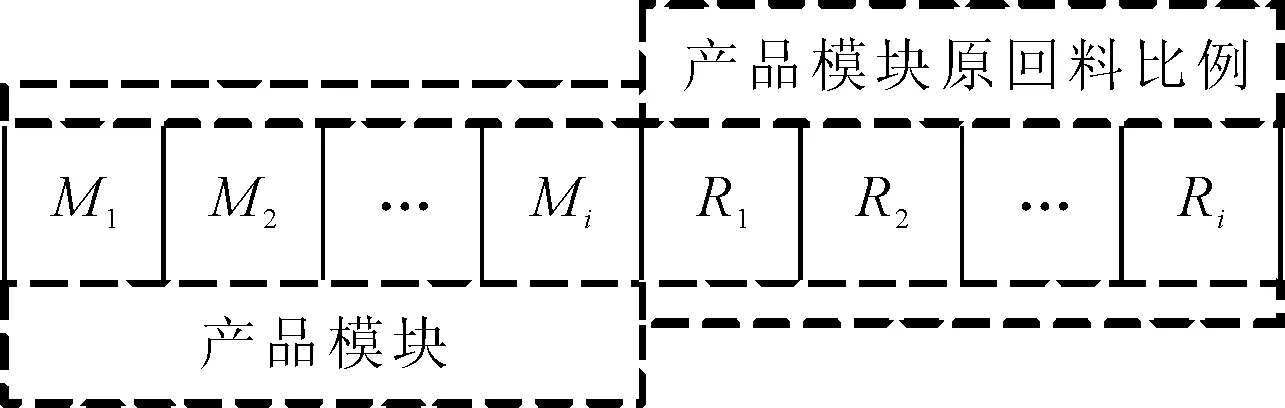
图2 产品配置方案基因编码

2.2 算法描述

2.2.1 选择算子

为保留种群中的优秀个体，采用一种精英保留策略与锦标赛机制相结合的选择算子。在生成交配池过程中，优先将非支配序为1的个体放入交配池，在剩下的父代中通过锦标赛机制选择更优秀的个体，直到交配池数量达到标准种群大小。

2.2.2 交叉算子

采用单点交叉的方式，从交叉操作池中随机选出两个染色体，生成一个随机值，根据随机值的大小是否满足交叉概率来决定是否进行交叉操作。随机指定一个位置作为参与交叉操作的父代染色体的交叉点，交换父代染色体在交叉点上的基因值，产生子代染色体，交叉过程如图3所示。

图3 交叉操作

2.2.3 变异算子

采用随机多点多项式变异算子，在交叉生成的子代染色体上，随机选取1到L个位置进行多项式变异，L取决策变量个数的三分之一。多项式变异公式为：

xk′=xk+δ(uk-lk)

(10)

δ=

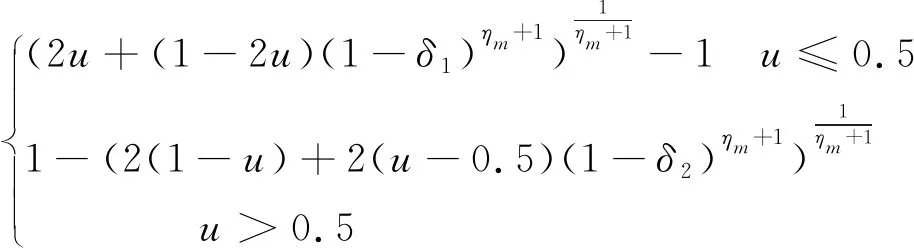
(11)

式中：δ1=(xk-lk)/(uk-lk)；δ2=(uk-xk)/(uk-lk)；uk、lk为变量xk的上下限；u为[0,1]区间内的随机数；ηm为常数，表示分布指数，此处取11。

变异操作如图4所示。

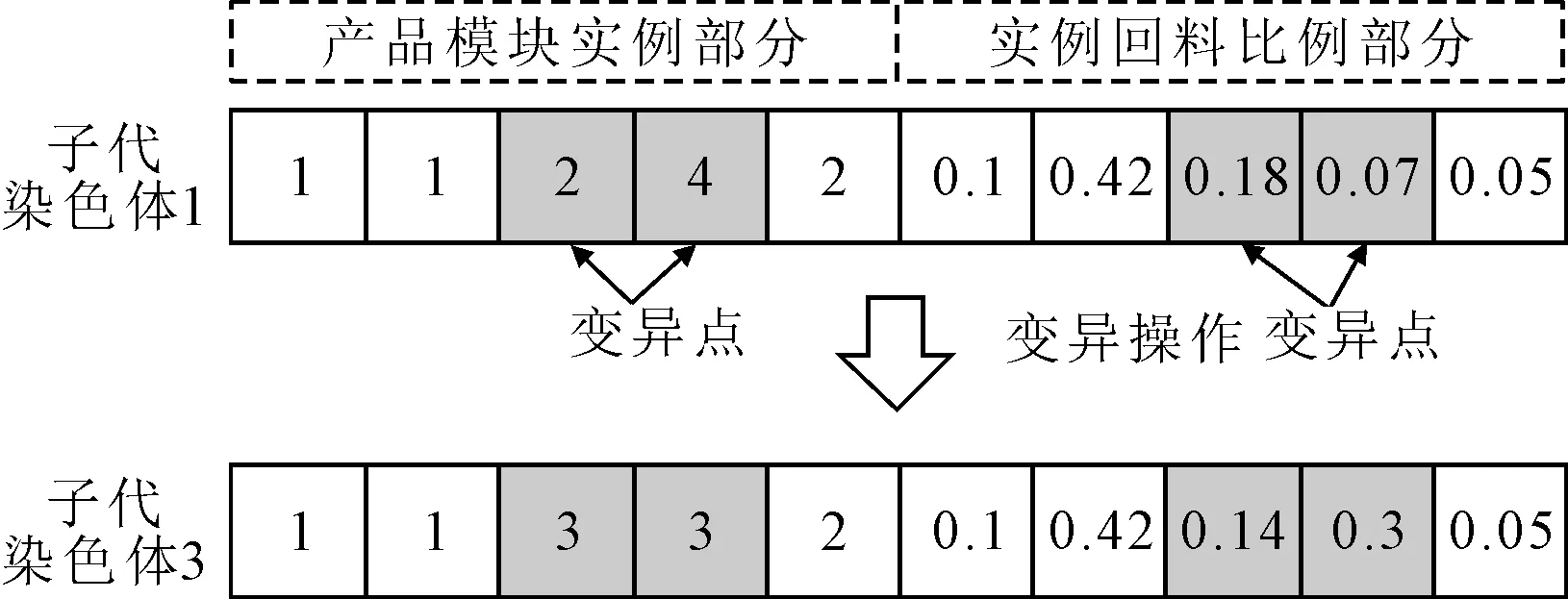
图4 变异操作

2.2.4 局部搜索算子

针对NSGA-III的不足，笔者提出了一种基于powell法的自适应局部搜索算子。在算法迭代初期，较大的步长可以在全局范围内搜索，使计算结果快速靠近Pareto前沿。随着迭代次数的增加，步长逐渐缩短，个体在自身附近搜索，提高了种群逼近Pareto前沿的能力。根据迭代次数自适应调整步长。步长ψ计算公式为：

ψ=0.1+0.9exp^(-3g/G)

(12)

式中：g为当前迭代次数；G为总迭代次数。

局部搜索算子的步骤为：

步骤1检查是否满足局部搜索条件，若满足，进行后续操作；若不满足，直接进入下一次迭代。根据当前迭代次数，确定搜索步长的范围ψ。

步骤2筛选种群中的Pareto第一前沿个体，以个体作为搜索中心Q0，确定一组方向Di(i=1,2,…,n)，n为决策变量个数；

步骤3从初始点Q0出发，沿着方向Di进行一维搜索，得到结果Qi，局部搜索变异公式为：

xk′=xk+rand(ψ)(uk-lk)

(13)

式中：rand(ψ)为取值在[-ψ,ψ]之间的随机数。

若Qi不在变量上下限范围内，对Qi进行越界处理，越界处理公式为：

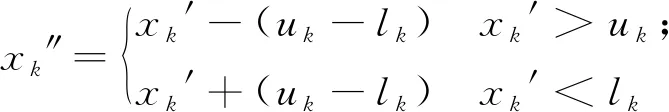
(14)

步骤4将每一次的搜索结果与搜索中心合并后，根据选择算子，选取出最优个体代替Q0。

3 案例应用与分析

3.1 算法对比

笔者采用6个带偏约束的数值MOEA(multi-objective evolutionary algorithm)测试函数集[11]作为测试函数，并在所建立的数学模型中加入了一个随机算例。改进NSGA-III算法与非支配排序遗传算法III、布谷鸟搜索算法CS、基于Pareto改进的多目标离散布谷鸟搜索算法(Parteo-IMODCS)[12]4个算法在每个测试函数下独立运行10次，取每次运算的ER(error ratio)和IGD(inverted generation distance)计算平均值作为测试结果。如表1所示，在多数测试函数下，改进NSGA-III算法的评价指标优于其他3种算法，证实了改进算法的合理性与有效性。

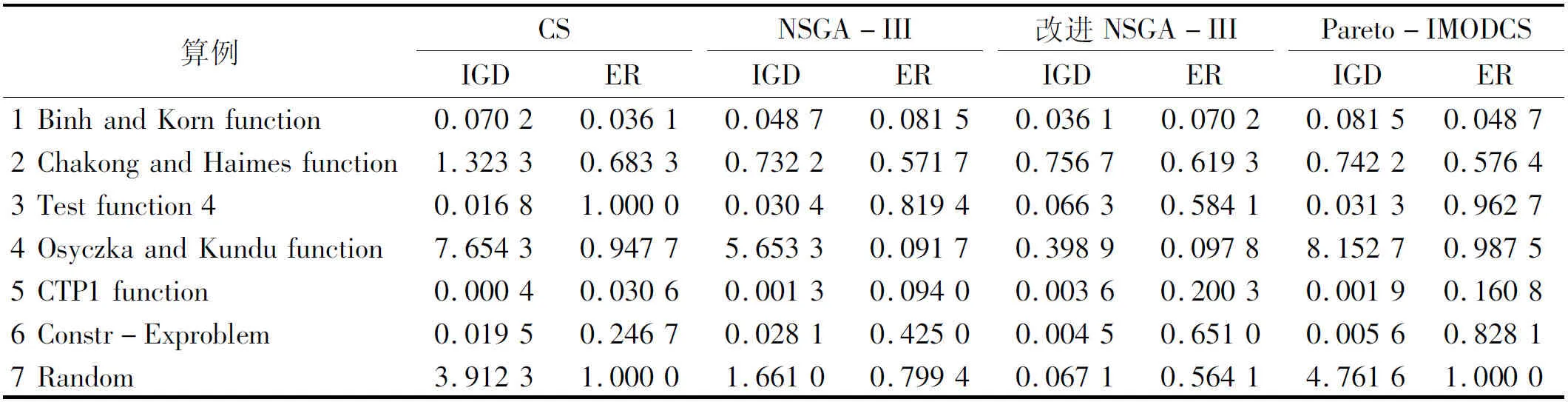
表1 算法对比测试结果

3.2 企业实例应用

针对本文建立的精密过滤输液器产品配置设计问题多目标多约束优化模型，以某医疗器械制造企业产品为例，企业生产的精密过滤输液器共有15个模块。采用笔者提出的改进NSGA-III算法进行仿真求解，获得配置方案的Pareto前沿。算法运行环境为Windows 10，Intel(R)Core(TM) i5-8400 CPU @2.80 GHz，16 GB内存，编程语言为Matlab 2018b。

取企业期望利润率β=20%，约束条件为客户可接受的价格Ce=16.7，客户可接受的可靠性Re=200，客户可接受的生产时间Te=0.998，可用原材料库存Wy=25，可用回料库存Wh=12，模块1的实例3与模块4的实例3为依赖关系(x1,3-x4,3=0)，模块4的实例3与模块9的实例2为互斥关系(x4,3+x9,2≤1)。优化结果如图5和图6所示，可以看到Pareto前沿较为均匀地分布在可行解空间中，成本、时间、可靠性3个目标函数的平均值随着迭代次数的增加而变化，并随着算法的寻优逐步收敛，最终进化曲线趋于平直线。

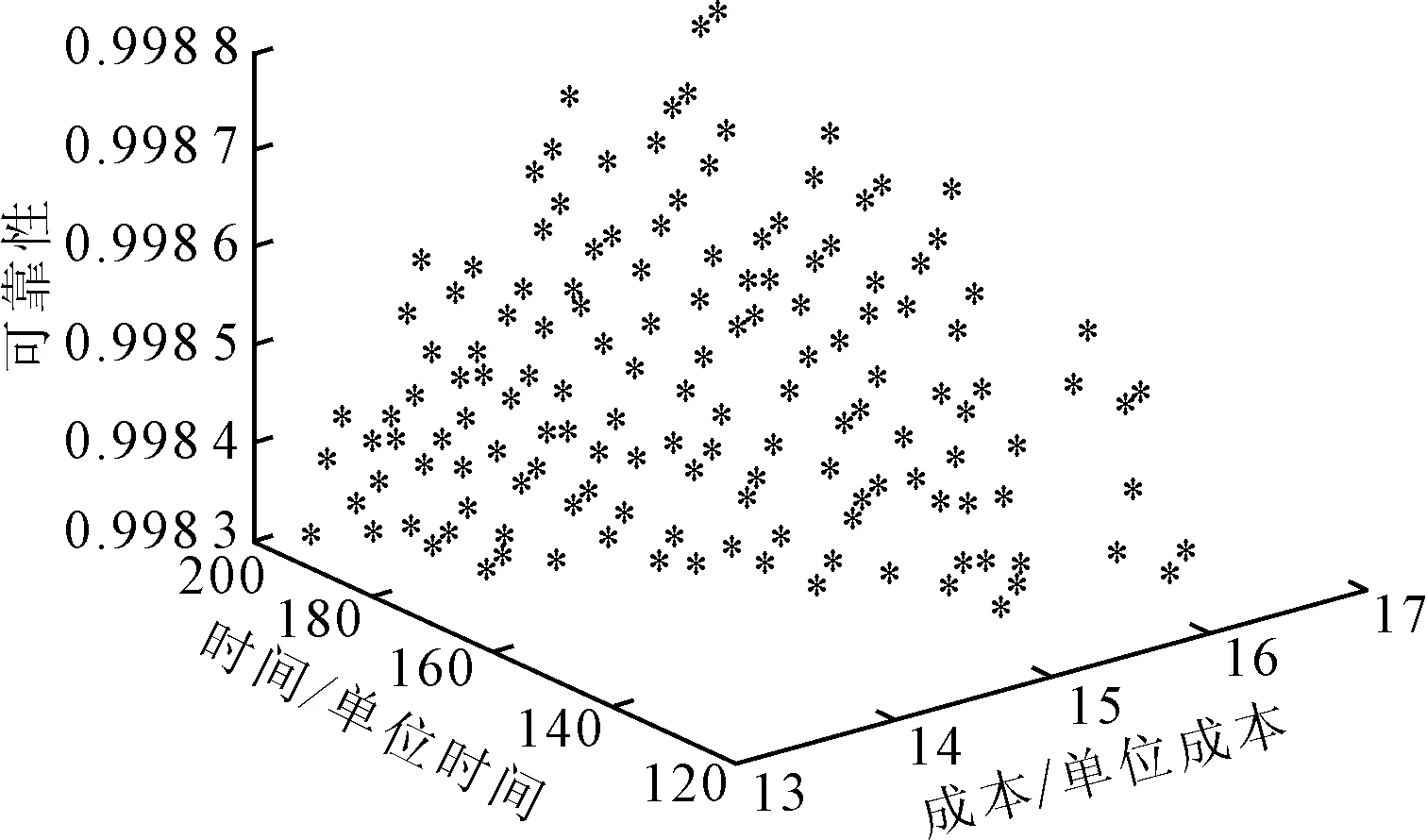
图5 精密过滤输液器产品配置优化解集

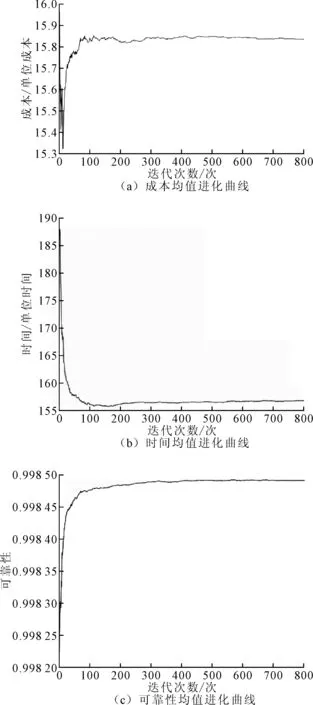
图6 各目标函数均值迭代曲线图

4 结论

在传统的产品配置优化设计研究基础上，针对医疗器械高可靠性的特点，将可靠性作为产品配置方案求解的目标函数建立模型。针对实际产品配置中存在的成本、时间等约束，采用惩罚函数法与多目标优化法结合的方式处理约束条件，通过约束违反度将约束条件转化为目标函数求解最小值。为了从大量的产品配置方案中快速获得满足企业与顾客需求的配置方案，笔者提出了一种改进NSGA-III算法求解产品配置问题。该算法在传统NSGA-III算法的基础上，加入了混沌搜索生成初始种群，保证了初始种群在决策变量空间上的遍历性与均匀性。在种群进化过程中加入多点多项式变异与基于powell法的自适应局部搜索算子，增强了NSGA-III算法的局部搜索能力。通过与NSGA-III、CS、Pareto-IMODCS进行对比，验证了笔者提出的改进NSGA-III算法求解结果的多样性与收敛性。最后，将改进NSGA-III算法应用于某医疗器械制造企业的实际案例，有效地获得优化的精密过滤输液器配置方案。