初一学生如何提高解决数学图形问题的能力

沈小燕

在数学课堂教学改革的背景下让学生达到预定的教学目标具有十分重要的探索意义。教师在教学工作中让学生自己找到问题、提出问题、解决问题进而培养学生解决数学图形问题的能力，通过不断改进教学方法和策略使学生自主解决问题的能力得到提高，进而达到高质量、有意义的数学图形教学。

一、初一学生解决数学图形问题的现状

教师在教学工作中不难发现，班上有些学生对数学图形问题有一定的心理障碍，缺乏自信心，碍于面子不好意思向教师提问等。还有一种现象就是学生普遍缺少质疑的兴趣，往往是教师讲什么就接受什么，主观性非常弱。这就导致现阶段初一学生在图形问题的学习中产生一定的障碍。

二、提高初一学生解决数学图形问题能力的策略

（一）培养学生的问题意识、探索意识、科学意识

教师要在教学中做学生的引导者和旁观者，可以让学生最大限度地自主完成学习任务，培养学生的问题意识、探索意识、科学意识、社会实践能力和良好的心理素质。在课堂活动中让学生保持良好的自主性、参与性，从而让学生掌握解决数学图形问题能力的品质和意识。这就要求教师在教学工作中找准切入的时机，鼓励和引导学生在课堂上对图形问题进行深入探索。通过这种方式可以让学生迅速地成长起来，培养对图形问题的探索和研究兴趣。

（二）让学生读懂数学图形题

在处理数学图形问题中往往能够发现数学图形问题会通过十分简练的表达来描述问题，这固然可以让学生在短短几句话中就得到一些等量关系和信息，不过也无形中提高了学生阅读理解的门槛。所以如何阅读数学图形问题是一个值得细细琢磨的问题。教师可以为学生创造机会来阅读数学图形问题，养成学生对数学图形问题的阅读习惯，重视数学图形问题中给出的信息。

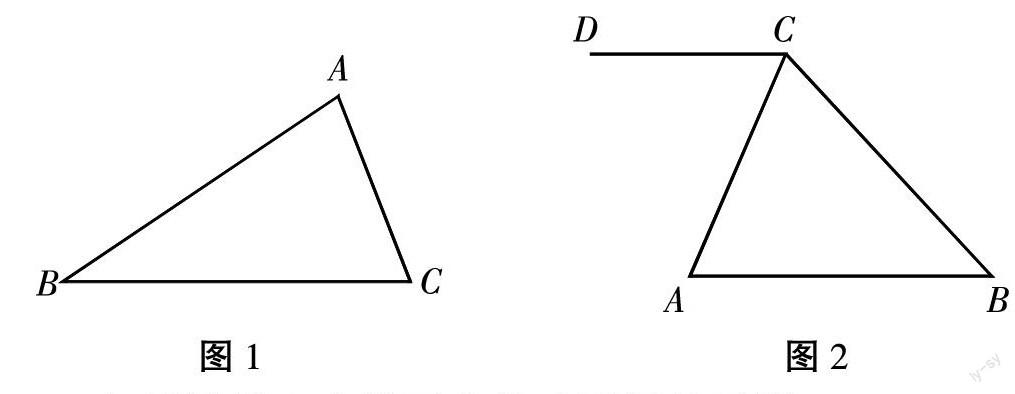
例如，在数学七年级上册第四章“几何图形的初步认识”中，在学习以及进行练习的过程中，教师要给予学生一定的引导，帮助学生分析题目并理解题目。如图1，我们已知△ABC由三条线段构成，请判断三角形三条边的关系，AB+BC  AC，AB+AC  BC，BC+AC

AB。教师引导学生在初次见到线段长度比较问题时可以采取使用直尺进行测量的方式，学生可以清晰地得出两条线段的和大于第三条线段，从而得出三角形的性质“两边之和大于第三边”。该题目中，图形的出现是为方便学生理解线段的关系，同时辅助学生进行长度测量。通过教师的引导，学生可以清晰地找到解决问题的办法，从而达到解决问题的目的。

（三）让学生在学习中养成质疑的习惯

对数学图形问题保持质疑和思考的能力会提高学生的思维主动性，让学生学会解决图形问题的基本方法。通过对问题进行充分的分析才能有基础去解决图形问题。让学生的思维完全地发散开来，有利于学生认识到图形问题的全貌。

例如，七年级下册第五章“平行线及其判定”的练习题“∠ACD=70°，∠ACB=60°，∠ABC=50°。证明：线段AB与线段CD平行。（如图2）”这个图形问题中我们根据已有的条件∠ACB=60°，∠ABC=50°，以及隐藏条件△ABC的内角和为180°，可以得知∠CAB=70°，所以∠CAB=∠ACD，由內错角相等，两直线平行可知线段AB与线段CD平行。这个案例中学生初次接触这种类型的问题会忽略三角形内角和为180°这个隐藏条件，教师通过引导学生并为其提供一个条件再继续让他们进行思考，最大限度地让学生保持对数学图形问题的解题兴趣和自信心。

（四）培养学生分析提炼数学图形问题的能力

教师为学生营造自主性比较强的课堂氛围后，还要让学生对数学图形问题进行脱离表象的思考。这是因为解决数学图形问题需要学生有一定的抽象思维和理解能力。通过引导学生对数学图形问题进行分析达到让学生思维发散的目的，让学生对数学图形问题的理解更加透彻和深刻，从而达成教学目标要求。

通过培养学生的探究意识，使学生对数学图形问题可以进行多维度的思考，把握学习的方向，有助于学生更好地思索与探究数学图形问题，从而促进学生在初一开始重视对数学知识的学习，帮助学生养成数学综合素养。

参考文献：

董国兴.初中数学“图形与几何”教学问题探析[J].新课程（下），2019（11）：154.