借图促思 深度学习

【摘要】数学核心素养是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用的过程中逐步形成和发展的。小学数学教师需要让学生逐步会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。小学生的思维正处在由具体形象思维向抽象逻辑思维过渡的阶段。借助线段图等辅助图进行教学，能促进学生思维发展，培养学生的数学关键能力，提升学生的数学核心素养。本文以“倍的认识”单元整理与复习课为例，对如何借图促思，让学生深度学习进行了阐述。

【关键词】小学数学;倍;辅助图

作者简介：徐曙华（1976—），女，浙江省宁波市慈溪市南门小学。

“倍的认识”是三年级上册教材第五单元的内容。学生通过本单元的学习，需要学会运用相关知识解决实际问题。在教学时，教师应该找准基点，以辅助图为纽带，围绕“求一个数是另一个数的几倍”“求一个数的几倍是多少”这两个基本问题，引导学生梳理本单元的知识脉络，让学生明白“求一个数是另一个数的几倍”即“求一个数里面有几个几”，需要用除法来计算，“求一个数的几倍是多少”即“求几个几是多少”，需要用乘法来计算，从而构建倍的数学模型，培养学生的数学应用意识。

一、直观感知，凸显本质

笔者在学生初次学习倍的概念时，已经借助实物图、示意图，通过数一数、圈一圈、说一说等活动，让他们对倍的本质有了初步感知[1]。笔者在引导学生复习之前设计了未标注数据的线段图，以直观地展示两个量之间的关系;在教学时引导学生将关注点放在“一个量里包含几个另一个量”上，从而理解倍的相关知识。

（一）片段1

师：（向学生展示图1的内容）请同学们估一估，第二行的长度是第一行的几倍？

生1：第二行的长度等于3个第一行的长度之和，所以第二行的长度是第一行的3倍。

在片段1中，学生运用已有知识，通过观察、比较的方式得出了结论。教师在教学时应该帮助学生掌握标准量的判断方法，引导学生将第一行看作1份，观察第二行中有几份。教师通过这样的方式，可以让学生明白第二行中有几份，就说明第二行的长度是第一行的几倍，进而了解“一个量里包含几个另一个量，这个量就是另一个量的几倍”的本质，巩固倍的概念等知识。

（二）片段2

师：（向学生展示画有2颗黄豆、6颗绿豆的图片）如果将这2颗黄豆看成1份，那么绿豆能被分成几份？请同学们试着用笔在图片上画一画。

生2：我认为可以将绿豆2颗2颗地圈起来，就能发现绿豆被分成了3份，绿豆的数量是黄豆的3倍。

师：刚刚我们了解了绿豆与黄豆在数量上的倍数关系。（展示画有8颗、14颗、20颗绿豆的三张图片）现在，请大家想一想这三张图片中的绿豆能被分成几份呢？为什么这三张图片中绿豆的数量分别是黄豆的4倍、7倍、10倍呢？

生3：因为我们将2颗黄豆看成1份，所以只要算出绿豆中有几份，就能得到绿豆的数量是黄豆的几倍。

在开展数学教学的过程中，教师除了借图促思，加深学生对所学知识的理解，让学生深度学习，还需要提升学生的逻辑思维能力、动手实践能力等素

养[2]。在“倍的认识”单元整理与复习课中，笔者让学生通过观察、动手、思考、分析的方式，探究了片段1中第二行与第一行、片段2中绿豆与黄豆的倍数关系。利用线段图、实物图等辅助图，可以让学生对课堂内容形成直观感知，凸显知识的本质。

二、借图变换，理解本质

在片段3中，笔者利用标有数据的辅助图，引导学生解决变式1和变式2两道题，通过改变比较量和标准量，让学生进一步认识倍，理解倍的本质。

学生在解图2中的题目时，需要找到标准量，用笔圈出份数，发现红花与黄花的倍数关系，学会求一个数是另一个数的几倍，从除法的角度理解倍的概念，认识到倍涉及两个数量的相互比较，进而巩固所学的知识。

（一）变式1

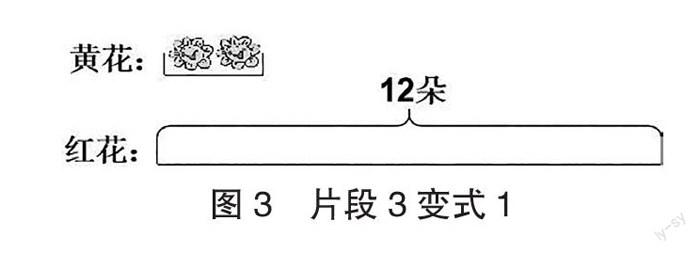
师：（向学生展示图3的内容）同学们，对于变式

1，你们是怎么想的？

生4：我认为需要算出12里面有几个2，即12÷2

=6。所以红花的朵数是黄花的6倍。

（二）变式2

师：（向学生展示图4的内容）对于变式2，你们又是怎么想的呢？

生5：这道题需要我们计算12里面有几个3，即12÷3=4。所以红花的朵数是黄花的4倍。

师：为什么变式1和变式2都是通过除法运算来求解的呢？

生6：因为这两道题均求的是红花的朵数是黄花的几倍，需要我们判断一个数里面有几个几。

在上述过程中，学生发现虽然例题中黄花和红花的朵数在变化，但是需要求解的问题没有变，所以解题思路、计算方法没有变;求一个数是另一个数的几倍需要用到除法。

三、借图比较，建立联系

在引导学生借助辅助图复习完上述内容之后，笔者让学生在片段4中比较如图2和图5所示的两道倍数问題，旨在拓展学生思维，帮助学生在解题的过程中找出这两道题的联系，优化思维过程。

师：（向学生展示图2和图5的内容）请同学们比一比这两道题，说说你们有什么发现。

生7：我发现例题1给出了黄花和红花的朵数，需要求红花的朵数是黄花的几倍;在例题2中，已知苹果的个数，并且草莓的个数是苹果的3倍，需要求草莓的个数。这两道题都和倍有关。

生8：我认为在求解例题1时，需要算出6里面有几个2，要用除法;在求解例题2时，需要算出3个8是多少，要用乘法。

笔者以辅助图的形式呈现这两道和倍有关的问题，引导学生进行比较，能够让学生明白这两道题的模型是一样的，但两者的不同之处在于类似例题1的题目是求一个数里面有几个几，而类似例题2的题目是求几个几是多少，从而建立问题之间的联系[3]。

四、活用模型，辨明图意

为了避免学生形成思维定式，笔者在片段5中运用倍比关系的模型、相差关系的模型、标准量和比较量互换的模型，設计了如图6所示的习题，以此让学生在辨析图意的过程中深化对倍的理解。

在片段5中，一方面，笔者注重引导学生体会标准量的内涵。笔者将习题的第3小题的第2个条件留空，旨在让学生结合第3幅线段图，找出基本的数量关系，进而得到本小题的第2个条件为“男生人数是女生人数的4倍”;并且，在将其与第1小题中的“女生人数是男生人数的4倍”这个条件进行对比时，让学生发现两者的标准量不同。另一方面，笔者注重引导学生了解倍比关系和相差关系。笔者在习题的第1小题中设计“女生人数是男生人数的4倍”的条件，在第2小题中设计“女生人数比男生人数多4人”的条件，旨在将倍比问题与相差问题相结合。这样不仅可以打破学生的思维定式，避免学生在遇到不同的问题时都只用同一种方法去解决，而且可以帮助学生巩固关于倍的知识，提升学生的自主学习能力。借助线段图，将数学问题与学生已有知识联系起来，有利于拓展学生的解题思路，让学生掌握有效的解题方法[4]。

“倍”是一个比较抽象的概念。笔者在“倍的认识”单元整理与复习课的教学中，巧妙利用辅助图，化无形为有形，凸显课堂知识的本质，能够加深学生对倍的认识，发展学生的思维能力，促进学生深度学习。

五、课后反思

学生在学习关于倍的内容时，大都已经掌握了乘除法的计算方法。部分学生虽然在之前的课堂学习中已经对倍有了初步的认识，但是未能进行深度的探究和学习，使得他们在复习相关知识的过程中容易遇到一些困难。针对这一问题，教师应该根据学生的理解能力、学习能力，从“倍的认识”这节课教学的重难点出发，引导学生进行深度学习。具体而言，教师首先可以让学生仔细观察图片，亲自动手操作，自主思考和深入分析相关问题，进而对课堂知识形成直观感知，凸显数学的本质;其次，结合辅助图，改变例题中的比较量和标准量，引发学生的思考，让学生深入理解倍的本质;再次，引导学生比较不同类型的倍数问题，建立问题之间的联系;最后，巧妙运用多种模型，让学生找出辅助图中蕴含的信息，进而巩固所学的知识。

此外，为了取得预期的课堂教学效果，教师应该围绕一些开放性问题，与学生共同探讨，以辅助图的形式呈现教学内容，以此提升学生的课堂参与度，活跃课堂气氛。教师需要一步步地引导学生掌握课堂的重难点知识，梳理知识结构，学会解决相关问题。

结语

总而言之，在小学数学教学中，教师可以利用辅助图及模型，以问题为主导，激发学生的学习兴趣，帮助学生有效理解重难点知识，熟练掌握解题方法，实现学习目标，促进学生深度学习。同时，教师要注重提升学生的思维能力、探究能力和问题解决能力，增强学生的数学应用意识，从而培养学生的数学核心素养。

【参考文献】

[1]郑毓信.数学深度教学的理论与实践[M].南

京：江苏凤凰教育出版社，2010.

[2]孙昌识，姚平子.儿童数学认知结构的发展与教育[M].北京：人民教育出版社，2005.

[3]姜鸿雁.促进数学深度学习的课堂教学策略：以《尺规作图》复习课为例[J].教育研究与评论（中学教育教学），2019（02）：30-34.

[4]张俊俊.巧借数学思考工具 促进学生深度学习[J].家长，2019（32）：22，24.