“变教为学”化解面积单位教学难点
吴荣军

[摘 要]“公顷和平方千米”这个教学内容看似只是对面积单位的一次简单的升级扩展,但是教学起来却非常棘手,处处掣肘。主要原因是教师大多是让学生快速记忆这些面积单位名称及其进率,而舍不得花时间去让学生交流探究和自主建构。实践表明,“变教为学”能化解面积单位教学难点。
[关键词]变教为学;面积单位;进率
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2022)14-0055-03
常见的面积单位包括平方厘米、平方分米、平方米等,学生对它们之间的进率了如指掌,都知道相邻两个面积单位之间的进率为100。对于面积单位之间的进率为100,教师进行了一次次推导,主要是通过长度进率10的平方推演出面积单位进率为100。一次次的图形验证,让这一进率关系成为师生共识,但是到了“公顷”这里,就陡然变成10 000的进率,而且在名称上也出现巨大变化:公顷不再沿用平方前缀,唯一不变的就是定义描述——边长为100米的正方形的面积是1公顷,边长为1千米的正方形的面积是1平方千米。虽然公顷与平方千米之间的进率出现一些变化,但是公顷与平方千米之间的进率仍是100,其推导也并不难,故照旧可以沿用以前的推导经验。
这看似寻常不过的教程,画几个正方形就可以直观演示和证明,学生学起来也驾轻就熟,条条款款如数家珍,但是学生一到应用就漏洞百出,频频出错。经梳理发现,错误主要集中在三个方面:(1)对于公顷这个生面孔、新称谓,学生很容易选择性失忆;(2)学生分不清平方千米和公顷到底哪个是“上級”,哪个是“下级”;(3)学生容易思维定式,常将公顷和平方米之间的进率默认为100。事出有因,这些错误的出现是有缘由的,仔细分析,就会发现,学生以前学过的面积单位,包括平方厘米、平方分米、平方米以及现在新增的平方千米,无一例外都对应着一个长度单位,无论是在名称上还是在定义上都是从长度单位扩展衍生而来的。只有“公顷”是名副其实的“独行者”,它没有一个长度单位与之对应(如表1)。
对此,学生就会按序排座,将公顷和平方米之间的进率纳入整个进率体系之中。公顷和平方千米这两个面积单位,一般只出现在工程建筑面积或者土地面积核算中,学生需要想象才能建立表象。因此,就会造成这种局面:对于公顷和平方千米,学生可以快速记忆,但是记忆维持的时间非常短暂,一旦时过境迁,就会遗忘,甚至以前建立的表象和积累的经验也都会从潜意识中消退,或者从学生的认知结构中解体。为了让学生将“公顷和平方千米”的相关知识点纳入认知结构中,形成深刻的印象,笔者借用“变教为学”的模式对公顷和平方千米的教学进行重构,以直观操作活动为载体,让学生完整经历知识的形成与发展过程。
活动一:自由表达,唤醒旧知
1.目前你学过或者知道哪些面积单位?你可以把它们全部罗列出来吗?
2.你知道这些面积单位的换算进率吗?尝试用自己喜欢的方式表达出来,形式不拘。
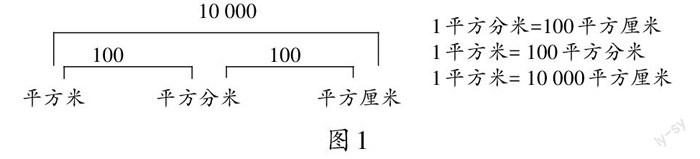
这个活动看似简单直接,却蕴含着无穷的玄机和奥妙。学生在回顾以往学过的面积单位时,会唤醒所有对于面积单位的记忆(如图1),包括当初如何定义面积单位,如何推导面积单位之间的进率,如何运用直观的正方形来度量其他图形,这样所有相互关联的知识都会一一闪现,无形中巩固强化了学生的已有知识。这样,没有限制任何形式和表达方法让学生说出相关面积单位的进率,学生可以根据自己的个性化理解将模糊的知识表象和脉络较为清晰地呈现出来。正因为不拘形式,所以学生才能有机会将自己相关的记忆激活,旧知也才能被最大限度地提取。“一千个读者心中就有一千个哈姆雷特”,学生可以用自己擅长的方式来诠释知识,每个人都有发表见解的机会,过去那种优等生替所有人代言的局面一去不复返。学生倾其所能,将自己的所学毫无保留地展示出来后,就能实现新旧知紧密衔接,自然过渡。
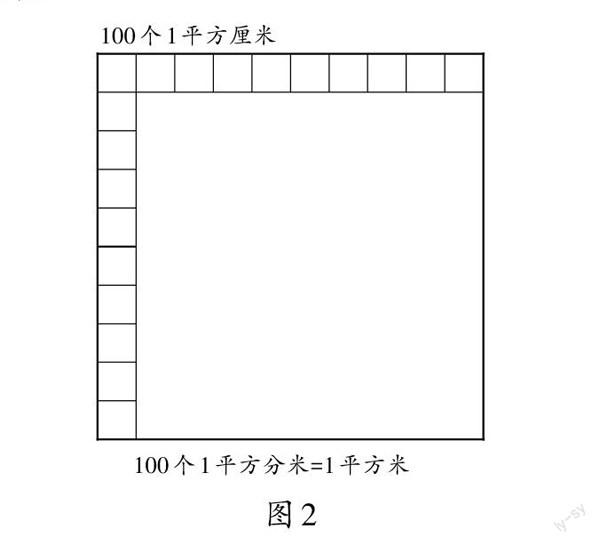
学生在长度和面积的学习中积累了相当丰富的经验,同时也积淀了许多丰厚的表象,如用边长为1个长度单位的正方形作为一个标准面积单位,对应的面积单位是在相应的长度单位上加平方前缀。至于进率的转化,也是结合长度单位的分割和面积单位的分切而直观推算的。如将1平方分米切成横竖10格,即10行和10列,那么1平方分米的大方块就被切成10×10的小方块,每个小方块就为边长为1厘米的正方形,也就是1平方厘米的面积单位(如图2)。这个过程就是长度和面积的“双切”,长度单位转化的同时面积单位也转化。学生回顾这些,可以再次将长度和面积融合,为后面公顷的学习建立良好的表象基础。虽然公顷没有适配的长度单位,但还是脱离不了这种直观结构,无非就是借用其他长度单位来构建(如边长为100米的正方形)。
活动二:自由讨论,引发冲突
师:平方米是否就是面积单位的“天花板”了呢?还有没有更“高级”的面积单位?如果有,这个面积单位应该如何定义?它的大小是个什么量级?可以跟同伴交流一下,说说自己的设想,或者说说自己的设计蓝图。
(学生的回答妙趣横生。)
生1:当然还有比平方米更高级的面积单位,它就是1平方千米,因为长度单位米过后就是千米,所以对应的面积单位平方米之后就应该是平方千米。同理,我们能将边长为1米的正方形规定为1平方米的面积单位,那么边长是1千米的正方形也可以规定为面积为1平方千米的面积单位。我的想法很简单:长度单位从小到大依次为厘米、分米、米、千米,那么按照对应原则,面积单位从小到大依次为平方厘米、平方分米、平方米、平方千米。
生2:好像有点不对劲。你看,100个1平方厘米拼接起来就合成1平方分米,100个1平方分米拼接起来就合成1平方米。如果按此规律类推,那么紧接着就应该是100个1平方米拼连起来,合成一个新的面积单位。
生1:那这个新的面积单位究竟应该是什么呢?
生2:边长为100米的正方形。
生3:你只是说了这个单位的几何形态,还没有给它命名呢?
……
师:大家认为平方米和平方千米之间需要设置其他的面积单位加以过渡吗?
(有的学生觉得应该有,有的学生觉得应该没有,有的学生则难以决断。)
这个活动给了学生自由的空间去建构面积单位的概念,学生结合面积单位的定义和形态,推理出新的面积单位的形状和大小,以及与之前的面积单位的顺承关系。从开始的特征定义法,到后来的从小单位到大单位的递推法,学生产生了认知冲突:100个1平方米拼接起来合成的新的面积单位,如果按照与长度单位对应晋级的命名法理应叫作“平方千米”,但是按照面积单位的几何图形直观定义法,1平方千米又应该是边长为1千米的正方形,显然这与100个平方米拼接起来的大小不符;100个1平方米的正方形拼接起来应该是边长为100米的正方形,而如果按照正方形几何定义的习惯,则这个面积单位似乎应该叫作“平方百米”,可是根据长度单位和面积单位一一对应加后缀的原则,在长度单位里又找不到一个叫“百米”的单位。至此,学生预感到在平方千米和平方米之间应该还需要一个过渡的单位。如果只是对知识的背记,学生只知其然不知其所以然,但是通过一系列的讨论交流活动,学生能按照自己的经验推测出“平方千米”这个面积单位,同时又发现“公顷”的影子。学生的学习在交流、质疑、修正中不断深入和成熟。
通过对长度单位和面积单位纵向和横向的对比,学生发现长度单位和面积单位在进率上也存在紧密的联系,这种联系与切分法是分不开的,每当相邻的两个长度切分成10的进率后,由于纵横相乘的关系,导致相邻的面积单位之间的进率变成100,于是,学生就形成动态认知结构:每当长度扩大10倍晋升到上级单位时,对应的面积单位就会自动晋升到上级面积单位。但是,到了米往上直接跳级到千米,中间没有十米、百米这样十进制的单位续接,因此,导致面积单位断层。于是,学生就会想到要按照既定的进制规则来补充新的单位,尤其是面积单位,在平方米和平方千米之间,跨度过大,必须创建新的单位填补这段空白。
活动三:扩充单位体系,完善认知
师:请大家将教材(人教版)翻到第34页,看能否找到蛛丝马迹。教材中为我们介绍了一些新的面积单位,这些都是比我们以前学过的面积单位更“高级”的单位,你们能想办法记住它们吗?
通过阅读相关章节,学生明白了1平方千米=1 000 000平方米 =100公顷,也从几何形态上明确了边长为100米的正方形的面积规定为1公顷的面积单位。但是,问题也随之而来(如图3)。既然边长为100的正方形可以用来定义面积单位,那么边长为10米的正方形也可以单独作为一个面积单位,这个面积单位该怎么命名呢?
师:这个边长为10米的正方形的面积的确存在过,它就是1公亩,这是中国的旧制面积单位。为了与国际接轨,新版教材已经摒弃了这个单位,采用新的单位——公顷。
生1:那么1公顷=100公亩。
师:你怎么将这个新的面积单位纳入原有的面积单位集合中?
生2:先把它们按从小到大的顺序排序,如平方厘米、平方分米、平方米、公亩、公顷、平方千米,每相邻的两个面积单位之间的进率都是100。
生3:这样一来就把平方厘米到平方千米之间所有的面积单位都排满了。
活动三使学生经历了知识生成和演变的过程,学生对面积单位间的进率有了深刻全面的认识。
活动四:建立表象,完善认知
师:用我们身边熟悉的场地印证1公顷和1平方千米的大小。
生1:居民广场的面积有2.2公顷。
生2:在电视里经常见到别人打高尔夫球,一杆子打下去,得花老半天时间去捡球,太费事了。现在看来,在将近1公顷大的草地上找球和捡球都是不容易的。
在谈到1平方千米时,学生想到了步行街,然后课后去步行街走了一遍,以它为标准想象1平方千米的正方形有多大。
学生这种身临其境的体验与感知,胜过教师任何形式的描述。
以上四个活动的设计是逐渐递进的,在活动开展的过程中,学生有足够的时间回忆旧知,自主建构新知,在不断反思的过程中感悟知识的生成经过和因由,学生从倾听者变为思索者,从死记硬背变成理解性记忆,真正实现了“变教为学”。
[ 参 考 文 献 ]
[1] 冯姗,于荣华.“认识面积单位”教学设计[J].中小学数学(小学版),2021(6):34-36.
[2] 尤佳.“简单组合图形和不规则图形的面积”教材分析与教学建议[J].小学数学教育,2021(Z4):102-104.
[3] 許英.数学深度教学:追寻单元整体目标阶段性达成:以三下《面积》整单元教学实践为例[J].数学教学通讯,2021(19):43-44,46.
[4] 孙开飞.拉长体验过程 促进深度学习:“面积单位”教学实践与思考[J].课程教材教学研究(小教研究),2021(Z4):50-53.
(责编 黄春香)

