是一一列举还是搭配计算？

薛陈香

[摘 要]在小学阶段的排列组合问题中，一一列举是最基础的方法。搭配算法公式是靠简易的列举操作来印证，而复杂的排列组合问题有时为了训练学生有序思考，不得不绕过搭配运算来一五一十地列举。正是这种错综复杂的微妙关系带来了学生的生成性教学资源。

[关键词]一一列举;搭配;有序;对比

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2022）14-0024-03

【教学案例】

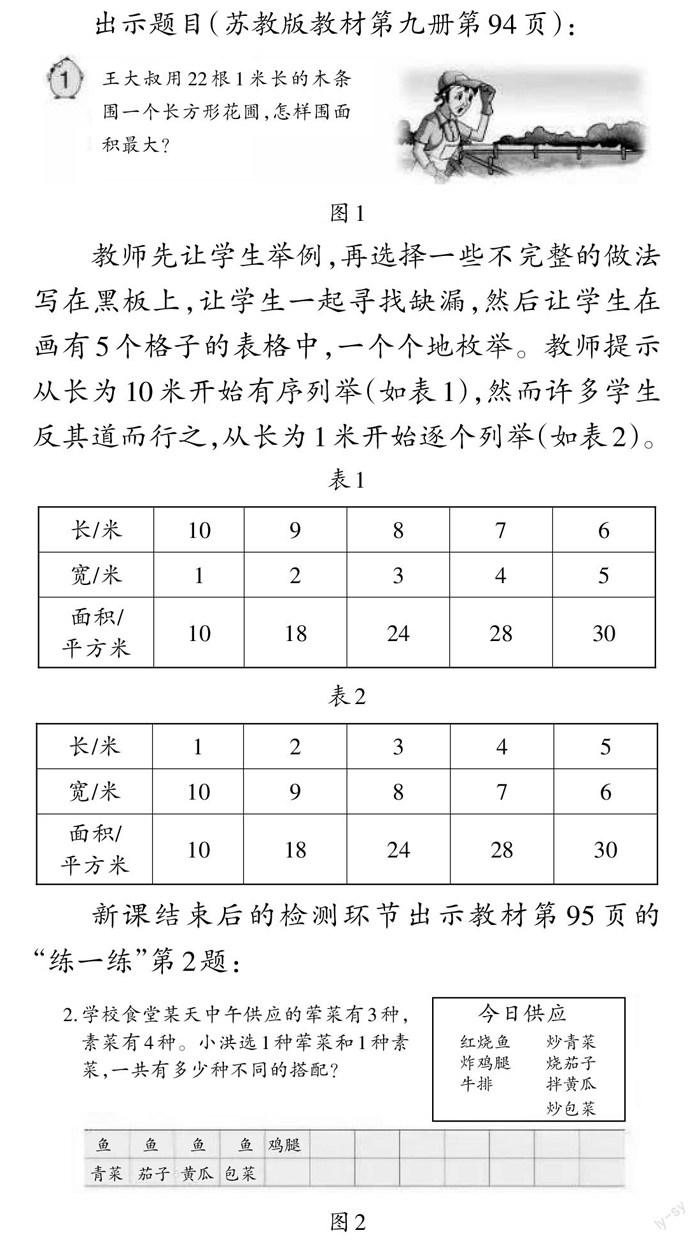
出示题目（苏教版教材第九册第94页）：

教师先让学生举例，再选择一些不完整的做法写在黑板上，让学生一起寻找缺漏，然后让学生在画有5个格子的表格中，一个个地枚举。教师提示从长为10米开始有序列举（如表1），然而许多学生反其道而行之，从长为1米开始逐个列举（如表2）。

新课结束后的检测环节出示教材第95页的“练一练”第2题：

不知道是因为一时大意，还是教师因轻视而刻意为之，原本写在习题后的提示语——“先填表，再回答”已然不见。教师发现一位成绩优秀的女生愁眉紧锁后立马上前询问：“到底出什么状况了？”怎料这位女生疑惑地说：“这道题与以前学过的一一搭配有什么分别呢？只需要列出乘法算式‘3×4=12就可快刀斩乱麻，何必这么大费周章！”此言一出，引来一阵骚动。教师错愕，呆了片刻，猛然醒悟，原来附录的注脚漏掉了，于是马上紧急补救：“教材有明确要求，需要一一列举！”……

一、逃避问题，无视生成性资源

课后，笔者对三位学生进行了访谈。首先问“从长为1米开始逐次往上递增”的学生：“你为何要从1米开始尝试？”他答道：“研究问题，不都是从最小开始的？”接着问“从10米长往下依序递减”的学生：“你为何要从10米长开始？”他喃喃道：“书上这么说的。”最后询问偏好乘法的女生：“你为何试都不试，一步到位，直接算出结果？”她理直气壮地说道：“本就是计算搭配方法，何必去一个个数！”……笔者与授课教师交流：“你为什么只展示部分作业？”对方理直气壮：“从10米长往下依序递减，这是书上的定论。更何况‘长 =1米、宽 =10米这种写法很反常，不符合语言习惯和我们对长和宽的通用定义！因此应该从最长的长度往下递减。” “对学生提出的用乘法直接算出结果，你为何敷衍搪塞、躲闪回避？”教师找了个理由：“一一列举是教材所定，不敢违逆，只不过我一时疏忽，制作课件时遗漏了……”

学生之所以会有疑虑，完全是因为对搭配方法计算与一一列举没有严格区分所致。搭配方法的算理揭示也是靠一一列举实现的，而复杂的排列组合问题也需要一一列举，解决这一症结的方法是渗透有序思考数学思想。有序思考是贯穿问题的主轴，例题中用周长一定来反推面积的做法，其实是对定长的拆分，这种拆分与搭配（组合）一样，需要有序思考。按照一一列举的做法，就要先暂定其中一个元素（长或宽），再降序排列或者升序排列，最后发现重复部分，然后剔除，这样一来就会对学生造成思维干扰：将搭配与拆分自动对比，而分配长和宽只能一一列举，无法像搭配那样直接计算。因此，在后面的一一列举一荤一素组合时，学生理所当然想到直接用公式计算，跳过一一列举。

二、 指明要求，迫使学生一一列举

本节课的教学目标是使学生通过一一列举解决问题，体验到有序列举的优势，并会根据有序列举速战速决，感受到一一列举的独特作用，进一步培养学生思维的有序性。

教师在备课时应该意识到，这一课程被编排在第九册的教材中，选择教学方式时，应考虑到学生的知识储备。反思以上教学片段，不难发现教师的预期与学生的基础之间存在差距。

在教学例题时，教师对教材亦步亦趋，一一罗列出各个知识点、划定重难点：首先强调基本构成单位——1米长的木条，提示长和宽不存在小数，然后就对数量“22”进行拆分，让学生明白这个22米不是别的，其实就是周长，最后着重攻克“面积最大”的难题，让学生明确“在众多的解法中寻找最优解，也就是在不确定、不唯一的面积算法中找到最大面积”。

按照五年级学生的思维特点，教学时更适合用“逆推追溯”的分析法，也就是剖析例题时，可从条件到结论顺推，但更应该从问题起步，逆推溯源，由最后的“确定面积”来反向求长和宽的具体值，从而在周长恒定时，一一列举长和宽的各种配对情况，并根据长和宽的守恒增减来反映面积大小的变化。

在教学例题时，教师无原则地迁就学生，任其信手列举，然后将散乱的列举拿来“开刀”，以此突出有序列举的优势。其实，有序思想早已存在（例如低年级的数数、因数和倍数等），对学生来说可谓是“老相识”。许多知识都隐含有序思维，可以说，有序性是数学思考的基本方法，也是数学研究的基础逻辑。

因此，笔者倡议：当列举比较多的围法时，要做到快刀斩乱麻，将所有可能一次性呈现，就必須唤醒学生有序思考的经验，直接开始制订有序列举的策略。不仅如此，提供路线比指导方法更管用，因为只要方向正确，方法是迟早可以得出的，无非就是多一道优化的手续。如此一来，学生的学习就不会呆板僵化，上述教学案例中教师的尴尬（必须按照教材从长度10米逐级递减）就会化于无形。教师可以顺应学生的生成性资源，从最小的1米开始逐渐递增，例如假设长为1米，通过（22-1×2）÷2就可以顺利计算出宽度为10米……至于教师忧虑的“‘长 =1、宽 =10这种表述很别扭”，完全对解题构不成威胁，因为“长”与“宽”只是人为命名的，数字大小没有规定。如果学生实在要钻这个牛角尖，教师可以提出“只需将长和宽对调即可”。

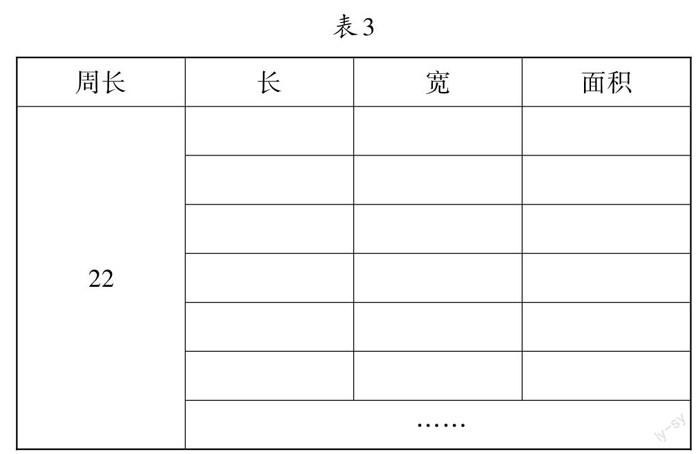
在备好的原始空表中，教师不妨改良一番，增设“周长”一栏（如表3）来拓展学生的思维，这样更利于凸显不变之中的变数。

在学生反馈时，再改弦更张“22÷2=11”，然后将11分解成两条邻边的长，对长和宽进行一一列举，这样就能直接与教材从长度10米开始递减的做法完美衔接。学生沿着自己的思路，从小到大列举到5的时候，会发现余下的都是长和宽对调后的重复组合，从而停手。反观教学案例，教师没有对教材列举到6就打住做出合理解释，发的5格表也带有很强的暗示性和误导性（似乎未卜先知，预知上限只有5种，根本否定第6种的存在）。科学的做法应是：取消表格格数上限，没有固定格数，由学生自己调整后确定。

正确处理好教与学的矛盾，才是调整教学的前提和依据，教与学的矛盾处理好了，教学流程自然就顺畅了。首先就是要处理好因果关系，这点很重要。到底是因为长和宽的组合存在多样性，所以导致面积不确定，还是因为面积本身存在不确定性，所以要去寻找长和宽的不同组合，这一点与一一列举的动机是分不开的。其实，从结论到条件的追溯法更能体现一一列举的必要性。其次，到底是先从无序列举中慢慢探寻有序列举，还是直接提示有序列举，这是基于学生经验所做的决定。既然是以培养和发展学生有序思维为宗旨，就不可能一蹴而就，需要学生积累有序思考的经验，所以此时可以直接要求学生有序列举，这样教学的目标性更强。最后，是对重复性的发现。即使出现重复列举，也不妨碍有序思维的训练，所以教师不需要事先阻止或者压制学生重复列举，待学生自然列举后，将重复的部分解释清楚并剔除就可，这样反而能让学生的有序思维更加严密。

三、对比方法，前后延伸

回顾教学案例可以发现，教师根本没有料到学生会有“搭配规律”的操作。有些学生受到提点，幡然醒悟，发现原有的方案“3×4=12（种）”更快捷。教材“舍近求远”，要求学生“先填表，再回答”，显然是为了绕开老路，重开新路，用新药治疗旧病，引导学生前后对比，揣摩搭配计算与一一列举的联系。然而，很是令人惋惜，教师不明其中原委，制作课件时漏掉了不可或缺的附带要求，导致意外发生。

出现这种状况，主要责任在于教师固执地按照教材行事，这恰是对学生思维的抑制。如果教师高瞻远瞩，抓住学生的思维火花，顺应学生，就能在对比后用事实说话——“再英明的策略，换了情境就要另当别论”，从而提高站位，为授课画上出彩的一笔。然而，令人遗憾的是，教师缺少全局观，只见到教材的先进性，而忽视其劣势，不能一分为二地看待问题;即使有了全局观，也觉得多一事不如少一事，免得节外生枝。如果没有出现意外，这道例题通常存在两种处理方式：一是完整出示习题要求，强令学生使用新方法，然后对比融通新旧方法，从而明白新旧方法都可行;二是将原问法“共有几种搭配？”改成“共有哪些搭配？”，迫使学生“就范”——只能列举。

好的教学应该能够前后延伸，除了“向前（已学知识）追溯”，让学生认清一一列举的不足，还可以利用例题2（如图3）“向后（未学知识）展望”。在学生尝试一一列举的策略后，教师可把数据扩大化，暴露出一一列举的短板：“等以后了解了最小公倍数，不用一一列举就可轻易求解。”如此，学生才会长进，并最终明白“随着知识的丰富，解题方法也会更先进”，并逐步形成稳健的思维习惯：首先研判“能不能”（一一列举的可行性评估），然后斟酌取舍。

教师还可以提点学生：“在一些情况下，一一列举成了唯一选择。例如教材第97页练习十七中的例题3（如图4）。”

至此，一一列举和搭配方法计算之间的关系总算捋顺了，二者都是为有序思考的培养服务的，但是区别也很明显，搭配方法计算虽然也用到一一列举来作为前期的直观演示，但这只是一种總结公式的手段，而且搭配方法计算的是总数，要的是一个统计结果，当需要一一判别各种不同的组合情况时，这个总数就不起作用了，而一一列举就十分适用。因此，只要将教材第95页的“练一练”第2题稍作改变，学生就会“乖乖”去列举：将“有几种荤素搭配？”改为“存在哪些荤素搭配情况？”。

总之，无论有无教学案例中的生成性资源，这节课都应该完成这样的目标——让学生灵活决策。当然，教师也要灵活教学。

[ 参 考 文 献 ]

[1] 陈赟.借助问题解决培养“有序”思维：以《一一列举的策略》一课为例[J].山西教育（教学），2021（8）：29-30.

[2] 冒金彬.说课：内容应重于形式[J].教育研究与评论（小学教育教学），2021（2）：37-40.

（责编 金 铃）