浅谈简便运算教学的实践与思考

朱红培

[摘 要]在教学实践中，多数学生对简便运算不理解，进而影响计算能力，而计算能力直接关系学生的数学学习能力，间接影响学生的数学核心素养。教学时，教师若能从学生内心的疑惑处出发，深度探究问题，并给出相应的解决策略，便能令学生学好简便运算，提高计算能力，有效培养思维的灵活性和创造性。

[关键词]简算;方法;思考

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）20-0083-03

运算律是苏教版小学数学四年级下册第六单元的内容，属于数与代数领域，是本册教材的重点内容。这个单元重在指导学生深度了解乘法、加法的基本内涵及其运算定律，使学生能依据定律进行简便运算。为激发学生的学习兴趣，笔者从班级学生的实际学业水平出发，设计多种生活情境，并引导其进入情境解决现实问题。在教学初期，学生虽然能正确理解运算定律的含义，并能应用所学的定律进行简便计算，但是随着教学的深入和简便运算类型的增加，学生综合运用各种运算定律进行简便计算时，问题便一点点地暴露。到底是什么阻碍了学生简便运算？带着这个问题，笔者走进学生的内心，了解他们的疑惑。

疑惑1：“老师，为什么要简便运算？”

在学完运算定律后，笔者有意识地给学生布置不同类型的简便运算题。随后，有个优等生向笔者抱怨：“老师，为什么一定要用简便方法计算呢？在计算的时候，我总弄不清楚哪道题该用哪个定律，有时候想得头都晕了！这么麻烦，还不如直接计算更快呢！”

疑惑2：“老师，我的简便运算错哪了？”

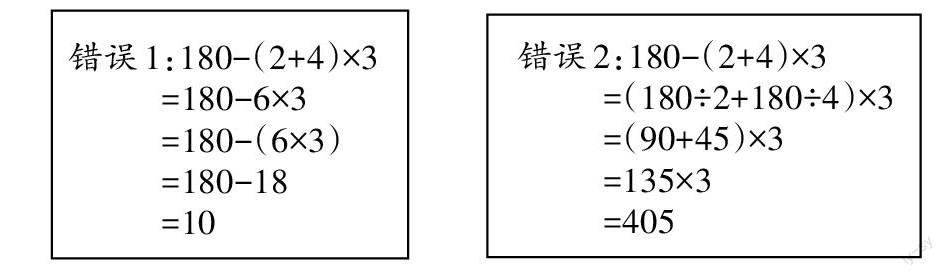
单元检测卷上有两道题失分严重：180-（2+4）×3，22×75-42×32。因为题目是“计算下面各题，怎样简便怎样算”，学生一看到“简便”二字，马上形成思维定式，所以得出了五花八门的错误答案，以第一题的错误情况为例。

学生想通过改变运算顺序和运算符号让计算变得简单一些，这说明学生有在努力寻找简便运算的方法。然而，有时过分地强调用简便方法计算，学生就会把本不能用简便方法的强用简便方法。

疑惑3：“老师，哪些题才能简便运算？”

如38×55+18×45，56×28×44×28，题目的要求是“计算下面各题，怎样简便怎样算”，可还是有两三个学生问：“老师，这题怎么简便运算？”

学生在分析习题结构时提出的疑惑，大多与之未完全掌握乘法分配律有关，且其认为的简便运算还局限在整百、整千的乘法中。由于学生对抽象的运算定律掌握得不到位，因此无法正确地判断哪些算式可以简便运算。针对上述情况，笔者采取了一些策略来展开简便运算内容的教学。

一、激发运算兴趣，让学生体验简算的“快”“趣”“爽”

要提升学生的计算能力，增强其数学认知，首先要引导其学会简便运算。基于学生思维发展的特殊性，教师设计生活情境让学生身临其境，可强化其对简便运算的认知与理解。

1.体验简算的“快”

笔者出示口算题目：23+15+278+14+26，50+43+50，78+26+22。在学生说出答案后，笔者问：“你是怎样口算的？你有什么秘诀？”在问答的过程中，笔者注重肯定学生的优秀之处，以及鼓励口算比较慢的学生继续加强口算练习，形成更强的口算能力。口算实质上是心算，是学生深层次理解“数”的基本性质和掌握算术运算规律的表现。不同学生的心算方式不同，但通过相互交流，优化方法后，学生能体验到简算带来的“快”感。

2.体验简算的“趣”

在课堂内引入竞赛活动，不仅能强化学生的竞争意识，还能巩固学生所学的知识与技能。因此，在教学简便运算时，教师可尝试开展数学竞赛活动，如“改错小能手”活动、“简算接力”比赛。除了课堂教学，教师还可在课后练习方面引入竞赛活动，如设计“简算天天练”活动。学生若能在连续5天的课后练习中都拿到100分，则可获得“简算高手”称号。实践证明，引入竞赛活动更能激发学生的学习兴趣，使学生更乐于参与简便运算。

3.体验简算的“爽”

在常规教学过程中，教师要注重引导学生了解运算的基本定律、性质以及特殊数据，并设计变式练习活动来帮助学生掌握和巩固所学知识。如在常规练习中开展对比练习活动，让学生比较分析容易混淆的题型，提高其运算鉴别能力;开展改错练习活动，让学生说出错误的原因以及可行性修正方法;开展分层练习活动，给不同层次、不同理解力的学生设计难度不同的练习，如给口算能力较强的学生设计思维逻辑较复杂的简算题：77×540+54×230，25×2626-26×2525，999×99×9。这些题既能使学生发散思维，又能激发其学习简便运算的兴趣。

二、加强基本训练，培养学生思维能力和良好的学习习惯

1.利用特殊数据，强化数感

准确理解数的基本含義、数的计算规律、数的大小与顺序、数的表达方法、数的表达模式、数的运算规律等便是数感。良好的数感能使学生更快地感悟和理解简便运算的内容及规律，并展开计算。如教师可引导学生识记常见数据——125×8=1000，25×4=100。

2.将计算与应用结合，强化应用意识

在现实生活中，大多数人到超市购物时都会预先估算自己要买多少钱的东西。从思维运算角度来看，人们预先估算是在确认手中的余额以及可以购买的东西，即现实需求。因为有需求，所以人们才会展开快速计算。同理，小学数学所提倡的简便运算也侧重于满足实际计算提高学生的需要。因此，培育学生的简便运算能力具有现实的必要性。

3.创设趣味情境，强化对比意识

引导学生深入具体情境学习简算，并不等同于单向灌输简算规律。如在教学运算律中的乘法分配律时，笔者创设了趣味情境。

在动物王国里，小熊开了一家森林超市，他要招聘1名有数学头脑的收银员。小猪和小兔前来应聘。小熊决定进行考试，择优录取。于是小熊出了这样一道题目：森林俱乐部要为裁判员买5套运动服，上衣是55元/件，裤子是45元/条，请你算算，一共要花多少钱？

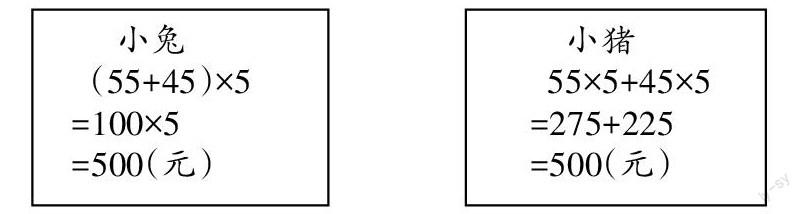
师：小熊刚读完题目，小兔就一口报出了结果，但小猪却算了很长时间，同学们，你们知道小兔是怎样算的吗？小兔为什么算得那么快？

（学生汇报，教师板书）

师：观察这两个算式，你有什么发现？

生（齐）：结果相同。

师：那这两个算式能不能用“=”连接起来？

生（齐）：能。

师（板书）：（55+45）×5=55×5+45×5。

可见，教师设计趣味情境，引导学生感受简算，能使学生更深刻地了解简算的作用。

三、掌握解题技巧

引导学生认知简便运算规律，做到真正学会简算，首先要让学生把握简算的解题方法。笔者依据教学经验，将简算的解题方法汇总成四个步骤：一判，二想，三估，四查。

“判”主要指判断并明确算式特征。学生简算真正的难点在于不能准确地判断算式的特征，导致所用简算方法错误。对此，在日常教学中，教师要注重培养学生认真审题的习惯。具体实践：教师出示题目后，首先引导学生判断题目是否能展开简便运算，若能简便运算，分析可用定律;若无法简便运算，分析具体的运算顺序。

“想”即思考，重在分析算式是否能进行简算，该选择何种方式、何种定律展开简算。如计算99×45+45这道题时，初看好像不能简算，但细看就会发现加号两边有共同因数45，故可以表示为（99+1）×45。

“估”即估算結果。在教学过程中加强学生的心算，既能提高学生的计算能力，又能提高计算的准确率。如计算101×54这道题时，教师可在学生展开简算前，让学生先进行心算。心算过程：54乘以100是5400，因此54乘以101的积一定大于5400。

“查”即检查结果，避免错误。学生做完简算练习后，教师要引导学生进一步检查计算方法与过程。长此以往，学生就能养成良好的检查习惯，提高计算的准确率。

四、加强辨析，寻求内涵

教师在教学中可适当地将同类型的内容安排在一起，让学生在比较分析中掌握知识间的联系与区别，从而有效地排除计算中的负迁移。

例如，学生总是分不清乘法结合律和乘法分配律的运用，对此，笔者出示25×（8×4）和25×（8+4）。先让学生观察这两个算式的异同点，再计算，最后让学生去掉两个括号，再计算出结果。通过两次计算对比，学生发现，前者去掉括号不改变算式的结果，而后者去掉括号则改变算式的结果。这样，学生就对这两个算式间本质的联系与区别有了深刻的认识。

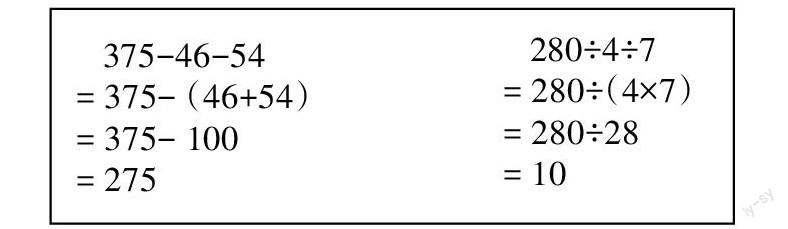
又如，在教学连除的简便运算时，可让学生将连减和连除联系起来对比学习。如下图，将连减和连除对应地联系起来，学生就不难掌握它们之间的关系，而学生掌握了连减的简便运算也就掌握了连除的简便运算。

再如，笔者针对教学中出现的情况，整理出一些学生容易出错的类型，并整合成对比练习。

学生通过题组训练，既可以厘清各种运算定律之间的关系，认清乘法分配律的本质，又可以养成先观察后动笔的计算习惯，清楚哪些算式可以应用简算，哪些算式不可以简算而应按运算顺序计算。如此，学生便可从“形式”过渡到“内涵”，深入知识“心脏”，追寻知识真谛。

五、借助经验，找准起点

1.借助知识经验

教学应该注重学生已有的知识经验，先找到学生知识的生长点，再经过同化和顺应，构建认知的结构。如教学乘法分配律时，学生已有的知识经验是“几个几”，这也是乘法分配律的核心所在。因此，教师可以把这个知识经验作为学生学习乘法分配律知识的生长点，引导学生用这个经验来解释如“（4+2）×25=4×25+2×25”等式左右两边为什么会相等。此时，学生解释为左边是6个25，右边是4个25加2个25也等于6个25。可见，教学只有植根于定律的意义理解，学生对算式结构特点的把握才能水到渠成。

2.借助生活经验

教师还可以借助生活经验来帮助学生理解乘法分配律。如让学生解决“一件上衣和一条裤子称为一套衣服，那么2套衣服里有几件上衣，几条裤子？5件上衣和5条裤子可以组成几套衣服？如果一件上衣120元，一条裤子80元，5套衣服需要多少钱？”这几个问题。在学生列出算式120×5+80×5和（120+80）×5后，教师便可自然地引出（120+80）×5=120×5+80×5这一乘法分配律最基本的模式。

六、抓住本质，构建雏形

由于小学生以直观形象思维为主，因此他们对许多知识的认识，常常先通过外显的形式开始，再逐步由表及里地去认识知识的本质。因此，在教学中，笔者会先引导学生从认识算式的外形结构入手，让学生初步构建乘法分配律的雏形。在学生得出（120+80）×5=120×5+80×5这个算式后，笔者再引导学生比较等号左右两个算式的异同点。当学生说出“左边算式是先算括号里的加法，再算乘法;右边算式是先算两个乘法，后算加法”时，笔者继续让学生探究两个算式有什么样的外形结构。因为此时学生对乘法分配律的认识只是停留在形式上还未达本质。只有当学生认识到左边是两个数的和乘一个数，右边是两积求和，即“两个数的和乘一个数=两积求和”时，学生才能构建乘法分配律的雏形。学生通过算式的外显形式到内在本质的变化认识，在外在形式上得到了初步感知，并找到了基本结构的本质，从而构建了乘法分配律的雏形，为深入认识乘法分配律打下良好的基础。

总之，任何教学都应促进学生的发展。作为教师，我们应站在学生的角度，深入挖掘宝贵的教学元素，积极引导学生探索实践。如此，学生所得到的将不再是冰冷的结论和花哨的技巧，他们将获得更多宝贵的数学思想方法、数学学习经验。因此，当指导学生学习简便运算内容时，教师既要使之理解并掌握运算技巧，又要激发其学习兴趣，如此才能真正落实课堂的实效性，提升学生的学习力。

（责编 覃小慧）