将数学知识“打包”

夏永立

[摘 要]只有把握好数学知识的整体框架，对教材内容进行“重组”，才能沟通知识之间的内在联系。教师应站在数学学科结构的高度，用结构的观点理解数学教材，用结构化的方法处理数学教材，将数学知识“打包”给学生，帮助学生理解数学知识的内涵，建构结构化的思维方式，不断提升思维品质，从而真正促进学生数学素养的发展。

[关键词]数学知识;加减乘除;结构化思维

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2022）20-0004-04

【课前慎思】

二年级的学生已经初步学习了加法、减法、乘法和除法的知识，知道了四则运算的意义，但并不清楚它们之间的内在联系。

在四则运算中，加法、减法、乘法和除法并不是孤立的，而是有着紧密的联系，是从前往后纵向联结的，也是由此及彼横向联结的，更是由部分和部分、部分和整体内部联结的。加法和减法互为逆运算;乘法和除法互为逆运算;乘法是几个相同加数的和的简便运算，它是从加法中“孕育”出来的;除法可以看作连续减去相同数的减法，它是从“减法”中生长出来的。为了让学生知道四则运算的本源，找到数学知识之间的连接点，将脑子中散状的概念串起来，组成知识链，形成完善的知识结构，笔者努力寻找数学之“根”，让数学知识生长出更多的“突触”，从而枝繁叶茂。

基于以上的思考，笔者设计了一节复习拓展课，通过整合知识板块凸显知识的系统化，帮助学生更好地掌握知识之间的内在联系。教学中，通过“我是谁？家在哪？还去哪？”三个“大问题”，帮助学生厘清数学知识的内在联系，让学生对运算概念的“前世”和“今生”了然于心，真正享受数学思考的乐趣。通过用一个圆形磁扣（下文简称“磁扣”）在数线上不断进行移动，使得学生在多种数学活动中理解四则运算的意义以及它们之间的内在联系，从而促进学生数学思维的发展。

【课堂实录】

一、操作观察，建立关系

师：一年级的时候我们学习了加法和减法，二年级上学期学习了乘法和除法。这节课我们一起来研究它们之间的关系。

出示数线图（如图1）：

师：你知道在数线上，0的“家”在哪吗？这个磁扣应该放在这条数线的哪里？（学生将磁扣放在数线图上的0处）

师（板书算式：0+1）：我是谁？（张贴卡片：我是谁？）

生1：0+1。

师：0+1的新“家”在哪里？（张贴卡片：家在哪？）请将磁扣移一移。（学生操作，将磁扣放在1的位置）

师：磁扣是怎样移动的？

生2：向右移动1格。

师：谁能表示这道算式的计算结果？

生3：0+1=1。

师：它（磁扣）现在怎样回到原来的“家”？谁来移一移？（学生把磁扣从1向左移动1格）

师：可以写出一道怎样的算式？

生4：1-1=0。

师：比较两次移动的过程，有什么相同和不同的地方？

生5：都是移动了1格，但磁扣移动的方向是相反的。

师：请说一道加法算式，并说说原来的“家”在哪里，现在怎样移。如果想回到它原来的“家”，怎样移？

师：请一位同学在数线上移动磁扣，别的同学用算式表示。（學生把磁扣从2直接拿到5）

师：谁能给他好的建议？

生6：磁扣应该从2移到3，再移到4，最后移到5。

师：磁扣在5的位置，又怎样回到原来的“家”呢？

生7：从5开始，向左移动3格。

师：刚才移动磁扣的过程，能用算式表示为2+3=5，5-3=2。

二、自主探究，沟通联系

1.沟通加法和减法之间的联系

师：在刚才移动磁扣的过程中，加法是怎样移的？减法呢？加法和减法之间有什么联系？

生1：加法是向右移动，减法是向左移动。

生2：加几就向右移动几格，减几就是向左移动几格。

2.沟通加法和乘法之间的联系

师：刚才移动磁扣的时候，都是一格一格移的，还可以怎么移？

生3：可以2格2格地移，3格3格地移……

师（板书：2+2+2+2=）：我是谁？我原来的“家”在哪里？究竟该怎样移磁扣呢？先在脑子里想，再在练习本的数线图上将移磁扣的过程画出来。

出示一位学生在数线图上标出移磁扣的过程（如图2）：

师：原来的“家”在哪里？现在的“家”在哪里？磁扣是怎么移的？

生4：原来的“家”在0，现在的“家”在8，向右每次移2格，移了4次。

师：那么，可以列一道什么样的算式？

生5：加法算式。2+2+2+2=8。

师：还可以列一道什么样的算式？

生6：乘法算式。2×4=8。

师：在移动磁扣的过程中，加法和乘法有什么不一样？

生7：加法是往右1格1格地移，而乘法是向右几格几格地移的。

师：乘法算式是怎么得来的？

生8：乘法算式是由加法算式“长”出来的，当相同的加数很多时，写起来不太方便，可以用乘法算式来表示。

3.沟通除法和减法之间的联系

师：观察2+2+2+2=8，现在的“家”在哪里？原来的“家”又在哪里？可以怎么移？

生9：现在的“家”在8，原来的“家”在0，也可以2格2格地移。

出示一位学生在数线图上标出移磁扣的过程（如图3）：

师：磁扣从8开始，向左2格2格地移，回到原来的“家”。你能想到什么算式？

生10：8-[2-2-2-24个2]=0。

师：还可以用什么算式表示？

生11：8÷2=4。

师：前面已经表示了加法和减法、乘法之间的关系，现在你能用箭头表示除法和减法的关系吗？

（学生尝试）

师：刚才移磁扣的过程，可以用减法和除法算式表示，它们之间有什么联系？

生12：除法可以看成是从一个数里面连续减去几个相同的数。

4.沟通乘法和除法之间的联系

师：结合刚才移磁扣的过程，观察比较2×4=8和8÷2=4这两道算式。乘法和除法有什么联系？

生13：乘法是向右几格几格地移的，除法是向左几格几格地移的。

生14：乘法是向右跳动磁扣，除法是向左跳动磁扣。

三、合作交流，深化认识

师（给学生每人一张画有数线图的练习纸，学生在数线图上移磁扣，并把移的过程用箭头表示出来，再写出相应的算式）：你还想几格几格地移？你能先写一道连加的算式，再根据这道连加算式写出乘法、减法和除法算式吗？

师：你想怎么移磁扣？

生1：从0开始移磁扣，向右3格3格地移，移了3次。

师：你打算怎样写算式？

生1：3+3+3=9，3×3=9。

师：它现在又想回到原来的“家”了，可以怎样移？

生1：从9开始3格3格地左移，移到0的位置。

师：你会写算式吗？

生1：9-[3-3-33个3]=0，9÷3=3。

师：这些是什么算式？

生2：加法算式、减法算式、乘法算式和除法算式。

生3：我是一格一格地移的，加法算式是1+1+1+1+1+1=6，减法算式是6-1-1-1-1-1-1=0，乘法算式是1×6=6，除法算式是6÷1=6。

生4：我是4格4格地移的，移了2次。加法算式是4+4=8，减法算式是8-4-4=0，乘法算式是2×4=8，除法算式是8÷4=2。

师：它们之间有关系吗？

生4：加法和减法之间有关系，加法和乘法之间有关系，除法和减法之间有关系，除法和乘法之间有关系。

师：请尝试画箭头表示四则运算之间的关系。

（学生展示画法：从加法画一个箭头到乘法，表示由加法可以得到乘法;从减法画一个箭头到除法，表示由减法可以得到除法;加法和减法之间画双箭头，表示由加法可以得到减法，由减法也可以得到加法;乘法和除法之间画双箭头，表示由乘法可以得到除法，由除法也可以得到乘法。）

师：它们之间有什么样的关系？

生5：它们之间可以互相转化。

师：加减是互逆的，相反的;乘除是互逆的，相反的。但是，乘法又是由加法“生”出来，除法是由减法“生”出来的。它们就像一家人一样，关系非常密切。如果把加法比喻成爸爸，乘法就是儿子;如果把减法比喻成妈妈，除法就是女儿。

四、拓展延伸，迁移学法

师：刚才我们把磁扣从0向右移，还可以怎样移？

生1：向左移。

师：从0开始，向左移1格，请同学们大胆猜测，可以用哪一道算式表示？

生2：0-1。

师：0-1等于多少？

（许多学生说“-1”）

师：你们都知道负数了，那在哪里见到过-1？

生3：在電梯里，-1是地下一层。

师：0-2的新“家”在哪里？谁能移磁扣来表示？

生4：将磁扣从0向左移2格。

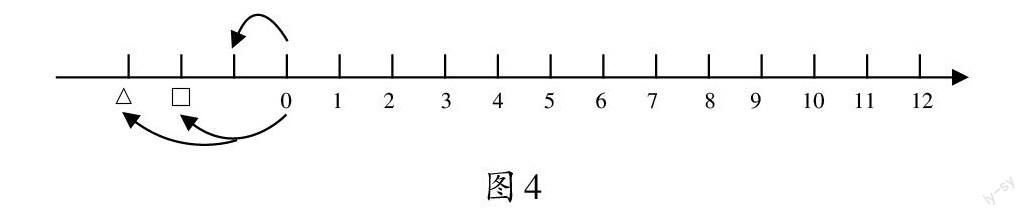
师：这个数是谁呢？我们把0-2的结果暂时用□来表示（如图4）。

师：0-3的“家”又在哪里？

生5：将磁扣从0开始移动，向左移3格。

师：这次我们用△来表示0-3的结果（如图4）。

师：你觉得是0-2的结果大，还是0-3的结果大？

生6：数线图上的点越往左边，数越来越小;数线图上的点越往右边，数越来越大。

师：其实数线图上还隐藏着很多的奥秘，等待你们以后去发现。

五、回顾反思，形成结构

师：这节课有新的收获吗？（学生回答略）

师：很多数学知识其实都不是彼此孤立的，是有联系的，将它们串起来，就会形成新的知识网络。

【课后反思】

这是一节单元复习拓展课，是笔者基于对教材的理解，创编的一个课例，以表达对“大单元”教学的一些思考。

一、素材少

四则运算的数学本质是什么？加法就是计数单位的累加，减法就是计数单位的递减，乘法是由加法“生长”出来的，除法是由减法“生长”出来的。

在这节课中，笔者利用一条数线和一个圆形磁扣，引导学生在数线上移动磁扣，从而感受加、减、乘、除之间的内在联系。简约和直观的素材，为学生后续的探究学习搭建了“脚手架”。

这样的教学设计能帮助学生明确知识之间的内在联系，将零散的数学知识串联起来，建立完整的知识网络结构。学生在结构化的学习中理解知识，就可以形成良好的数学素养。

二、空间大

这节课，采用“我是谁？家在哪？还去哪？”三个数学核心问题，引领学生进行数学探究，让学生的思维不断延伸。“我是谁”是让学生观察一道算式，进行思考。“家在哪？”是引导学生思考原来的“家”在哪里，新的“家”又在哪里，怎样在数线上移动磁扣才能够找到新的“家”：可以1格1格地移，也可以几格几格地移;可以从左往右移，也可以从右往左移。最后，“还去哪？”实现学习方法的迁移。也就是要不断开阔学生数学学习的视野，为中学学习有理数的加减法做好有效铺垫。

放手让学生独立操作和合作交流，给予学生自主学习的时间和空间。笔者先让学生自己写一道连加算式，再引导学生发散思维“由这道连加算式，我们可以想到哪些算式？”，然后让学生自由地在自己的练习纸上画线表示磁扣移动的过程。这种开放式的练习，就给了学生很大的思考空间，而不是让学生局限于某一道算式。学生通过交流辨析，对四则运算关系的理解会更加深刻。

在以往的教学中，笔者都是自己画箭头，这种教学虽然很顺畅，但是没有给学生一个具有挑战性的学习任务。在这节课中，笔者尝试让学生画箭头，学生在画箭头的过程中有对话、有交流，认识会更加深刻。

学生在动手操作、画图表征和交流分享的过程中，将碎片化的知识连成线、结成网、筑成块，建立了整体的结构化思维，形成了完整的认知结构。

三、思考深

从一道简单的加法算式“0+1”开始，通过“原来的‘家在哪里？”“怎样移动磁扣就可以找到新的‘家？”“新的‘家在哪里？”等问题，引导学生比较加法与减法的内在联系，进而发现乘法与除法之间的关系，勾连出加、减、乘、除四则运算之间的关系。

这节课不仅是让学生理解加、减、乘、除之间的关系，还通过在数线上的磁扣可以向0的左边移动引出负数。低年级学生对负数有一定的生活经验，所以这样的学法迁移，不是超纲，而是一种系统化的学习，真正实现了为迁移而教。

本节课呈现了加、减、乘、除之间的联系，培养了学生的推理能力和概括能力。在本节课中，学生掌握了探究知识内在联系的方法，积累了丰富的学习经验，就能利用这些经验进行大胆的“创新”，构建新的数学知识结构。

（责编 金 铃）