图“说”疑难杂症 图“感”建构模型

俞洁文 唐尾玲

[摘 要]“图感”具体表现为小学生对数学学习情境中“以图表意、以图表数、以数释图”的感知与理解能力。通过图“说”抽屉原理、图“说”周期规律、图“说”奇数偶数、图“说”“蝴蝶模型”，还原学生视角，培养学生的直觉思维，提升学生对数形关系的敏感度。

[关键词]图感;数形结合;建构模型

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2022）20-0023-03

本文关于“图感”内涵的认定基于三个方面的思考：一是学生关于数与图（形）之间关系的直觉;二是学生对数和形关系的敏感度及辨别能力;三是学生在运用数形结合中产生的一种对数学的理解。下面将结合人教版教材的教学实例，阐述数形结合在攻克学习疑难点和建构数学模型中发挥的作用。

一、 图“说”抽屉原理——可视化思维还原学生视角

数学广角作为小学数学的亮点内容，虽然拓宽了学生认识数学的视野，但其教学内容普遍存在容量大、难度大的问題，抽屉原理更是难中之难。蒋承飞老师在一次课堂教学观摩研讨活动中执教了“抽屉原理”一课，全课紧扣“总有”“至少”“苹果数与抽屉数的关系”三大问题展开探究活动，将数形结合与抽屉原理融合后引导学生进行探究，进而建立模型，有效突破了难点。

【教学片段】关于“总有”的认识

伴随3D打印弹珠游戏的介绍，课堂在学生喜爱的游戏活动中拉开帷幕。3D打印弹珠游戏的规则：有3个抽屉，给你3颗弹珠，只要有2颗弹珠进入同一个抽屉，就能中奖。

问题1：根据这个规则，你们最不希望出现什么情况？

问题2：有哪些情况能中奖？

问题3：为什么最不希望出现（1，1，1）？

蒋老师打破4颗弹珠、3个抽屉的常规教学方法，课始呈现3颗弹珠进入3个抽屉的情况，引导学生设想没有2颗弹珠在同一个抽屉里（即最不利的情况），唯有（1，1，1）一种情况，从而完成记录方法的介绍。这样，面对4颗弹珠、3个抽屉的情况，学生就能轻松理解“此时第4颗弹珠无论怎么放，总有1个抽屉里有2颗弹珠”，感受到最不利的情况中蕴含平均分的知识。

【教学片段】关于“至少”的认识

教材是直接出示抽屉原理的结论，并呈现两种思考方法：用枚举法证明和用假设验证推理。抽屉原理实际上是解决某种特定结构的数学或生活问题的模型，是一种数学思想方法。唯有让学生经历抽屉原理的探究过程，才能更好地发展学生的抽象能力和推理能力。这样，学生不仅能理解抽屉原理，更能感受归纳演绎的逻辑推理思维。

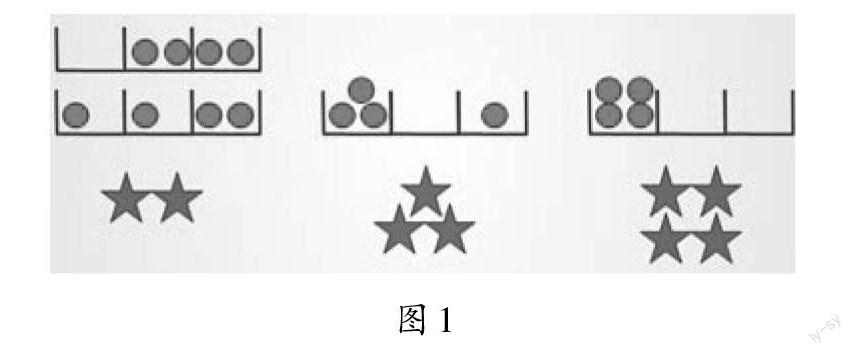
出示：4颗弹珠进入3个抽屉后分别获得幸运星的数量如图1。

问：玩一次游戏至少能获得几颗幸运星？“至少”是什么意思？

4颗弹珠放进3个抽屉只有图1的几种情况：当其中1个抽屉最多有2颗弹珠时，就获得2颗幸运星;当其中1个抽屉最多有3颗弹珠时，就获得3颗幸运星;当其中1个抽屉最多有4颗弹珠时，就获得4颗幸运星。至此，学生很容易得出“至少获得2颗幸运星”这一结论。而借助图形就能化解“在至多数中找至少数”这一难点，并总结出一个肯定的结论：把4颗弹珠放进3个抽屉里，不管怎么放，总有1个抽屉里至少有2颗弹珠。

抽屉原理教学的一个难点是建立模型，蒋老师将抽屉原理的两个核心关键词“总有”和“至少”分步展示，“总有”包含了所有的抽屉，“至少”包含了所有的情况，借助图形将看不见的思维可视化，就能还原学生视角，突破教学难点。

二、 图“说”周期规律——根据间隔天数推算星期几的新视角

学习“年、月、日”知识后，学生经常会遇到类似 “2012年2月1日是星期三，小明3月2日过生日，这一天是星期几？”的问题。这类问题有多种推算方法，如：运用月历特点找到与2月1日一样是星期三的日期有2月8日、15日、22日、29日，往后推，3月1日是星期四，3月2日是星期五。这种方法显然不适合天数过多的问题。如：利用计算推理，2012年2月有29天，2月1日到3月2日共计31天，头尾算1次经过30天，（29+2-1）÷7=4（星期）……2（天），2月1日是星期三，余2则往后推2天，是星期五。这种方法会让学生搞不清楚日期算头算尾的原理，也许今天记住步骤了，明天可能又忘了。反观一些循环现象的周期问题，学生并不觉得难，为什么关于日期的循环问题就屡屡出错？这时教师就可借助图表帮助学生直观理解推理的含义。

一变：从横排到竖列的演变。常规循环问题通常是横向排列的，从横排到竖列循环出现的规律相同，表述形式有变化，都是以“星期三、星期四、星期五、星期六、星期日、星期一、星期二”为一个周期不断重复出现（如图2）。

二变：增加日期与星期几相对应（如图3）。对于问题“如果1日是星期三，15日是星期几？”，就可利用“日期按自然数递进排列但不具备循环规律，星期具备7天一循环变化”的规律，当日期依附于7天一循环便同步产生了规律 。根据这个规律来推算， 15÷7=2（星期）……1（天），15日是第3个星期的第1天，即星期三。

三变：呈现生活中的月历（如图4）。对于问题“2012年2月1日是星期三，小明3月2日过生日，这一天是星期几？”，观察月历，每个循环从星期三开始，按照“星期三、星期四、星期五、星期六、星期日、星期一、星期二”的规律循环，2012年2月有29天，2月1日到3月2日共计31天，把31天放入7天一组的循环中，列式（29+2）÷7=4（星期）……3（天），所以剩余3天是第五个循环的第三天，即星期五。

上述推理过程，均先借助图表寻找“星期几—星期几”为一个7天的循环，再找出从头至尾的日期一共多少天，放入循环中推算经过n个循环余下几天，余下天数在第n+1个循环中重新排列，余下几天就排在第几。只要学生心中有一张图表，解决此类问题就不那么困难了。

三、图“说”奇数偶数——由图形表征奇偶数特征培养直觉思维

对于五年级下册第二单元的“和的奇偶性有什么规律？如何证明？”问题，教材要求运用舉例、借助几何直观的图示、说理等方法解决，从而引导学生认识两数之和的奇偶性的规律。学生通常会选用举例的方法，但是举例不能穷尽，而用字母说理涉及高难度的字母化简，因此借助直观的图示探究规律是比较合适的方法。

【教学片段】图形表征奇偶数

“秒杀比眼力”第一组：1个小正方形表示1，快速判断下面组合图形中（如图5）的小正方形个数是奇数还是偶数。

观察发现，偶数个小正方形拼成的形状是长方形或正方形，奇数个小正方形可以排成一行，排成两行总会多出1个小正方形。

“秒杀比眼力”第二组：1个小正方形表示1，快速判断组合图形中（如图6）的小正方形个数是奇数还是偶数。

在这两组“秒杀比眼力”题目中，学生体验到用什么样的图形可以表示奇偶数，以及如何用一个图形表示任意一个偶数或奇数。

用图形展现奇数与偶数的特征，充分将数与形结合起来培养学生的直觉思维，学生获得了简约而不简单的体验。

四、图“说”“蝴蝶模型”——化繁为简中提升数形关系的敏感度

五年级的多边形面积的计算，涉及组合图形面积和图形拼组后的阴影面积计算。如图7，正方形ABCD的边长是8厘米，正方形GCEF的边长是6厘米，求图中阴影部分的面积。

学生的解答：

图8-1的解答思路清晰：用大小两个正方形面积之和减去三个三角形的面积，得出正确的结论。图8-2的解答非常巧妙：连接AC得到梯形ACEG，以EG为底，阴影面积恰好等于三角形CEG的面积，也就是小正方形面积的一半。两种不同的解法反映不同的思维层次，如何让更多的学生掌握如图8-2的解答方法？教师可以对学生进行以下训练。

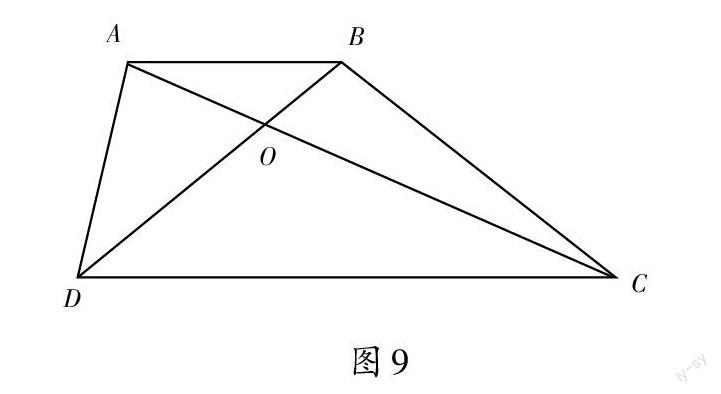
在图9的梯形中，面积相等的三角形有哪几组？学生喜欢称三角形AOD与三角形BOC为一对蝴蝶的翅膀，即“蝴蝶模型”。通过图形变式让学生体会等底等高的三角形面积相等，并推断出梯形中的“蝴蝶模型”左右两边的面积相等。将数与形结合建构模型，疑难问题变得简单，学生获得了成功的体验。

综上，教师要在教学中培养学生的“图感”——在数学情境中“以图表意、以图表数、以数释图”的感知与理解能力，通过建立“图感”助力学生理解现实生活中数与形的意义，理解或表述具体情境中的数量关系，建构数学模型，让学习深度发生。

（责编 金 铃）