小学数学实验教学有效路径探寻

黄月桃

[摘  要] 以“三角形边的关系”为例，文章提出了小学数学实验教学的基本策略，即引发猜想，让实验成为内在需求;实验设计，发挥实验教学的功效;实验分析，结出真理的“硕果”。文章通过以上策略，以使学生获得对数学知识的积极情感体验，获得解决问题的基本经验。

[关键词] 数学实验;三角形;小学数学

数学家波利亚说：“数学既像一门系统的演绎科学，又像一门实验性的归纳科学。”数学家欧拉说：“数学不但需要观察，也需要实验。”随着新课改的不断推进，数学实验逐渐成为打造高效课堂的重要途径。数学实验以实验探究为主要特征，承担着阐释知识本质、发展数学能力、积累活动经验的重任。它注重学生动手操作，在趣味性、实验性、挑战性的情境中大胆实验、积极思考，从而使学生加深对知识的本质理解，发展学生的数学素养。如何才能最大限度地发挥数学实验在教学中的功效呢？文章以“三角形边的关系”为例，论述了在课堂上贯彻实验教学的基本策略，期望能够起到抛砖引玉之效果。

[?]一、引发猜想，让实验成为内在需求

猜想是一种带有直觉性的思维形式，要求学生面临较为复杂的问题时，能够再现已有的知识储备，经过观察和分析，对问题做出大胆的猜想、假设和试探，从而为问题的解决提供方向性参考。要引发学生猜想，除了要求学生具有一定的认知经验和知识储备外，创设生动情境也是重要的条件之一。创设情境是实验教学的“开场舞”，教师应该结合学生生活实际创设生动、有趣的教学情境，在情境中引發学生思维冲突，使学生主动猜想，并产生运用数学实验验证猜想的强烈意愿，真正让数学实验成为学生发展的内在需求[1]。

在“三角形边的关系”的教学中，上课伊始，教师先引导学生从学具袋中任意选择3根小棒，看看这3根小棒能不能摆出三角形。学生在拼摆的过程中发现，任意3根小棒，有的能够摆成三角形，有的不能摆成三角形。这个时候，教师趁势提问：“你认为3根小棒能不能摆成三角形，与什么有关系？”学生开始讨论交流。有的学生认为，能否摆成三角形取决于最长的那根小棒的长度;有的学生则认为，与最短的那根小棒的长度有关;有的学生考虑到可能与这3根小棒的长度都有关系。就在学生各说各理，莫衷一是之时，教师进一步说道：“实践是检验真理的唯一标准。现在我们就通过数学实验来验证我们的猜想。”

教学中，教师创设情境，使学生在操作的过程中产生强烈的思维冲突：为什么有的一组小棒能够摆成三角形，有的却不能呢？由此引发学生主动思考，并产生各种猜想。就在学生处于一种“心求通而未得之意，口欲言而未能之貌”的“愤悱”状态时，教师顺势引入数学实验，就能够充分调动学生探究兴趣，为下一步数学实验的开展奠定基调。

[?]二、实验设计，发挥实验教学的功效

“没有行动，思想决不能成熟为真理”。实践与活动是数学实验教学的显著特征。数学实验设计应该将关注的焦点集中于学生学习的过程和方法，让学生在数学实验中有所发现，从而验证自身猜想的正确性[2]。

师：现在，我们通过实验来验证我们的猜想。我们的实验目标就是要验证3根小棒满足怎样的关系，才能摆成一个三角形。

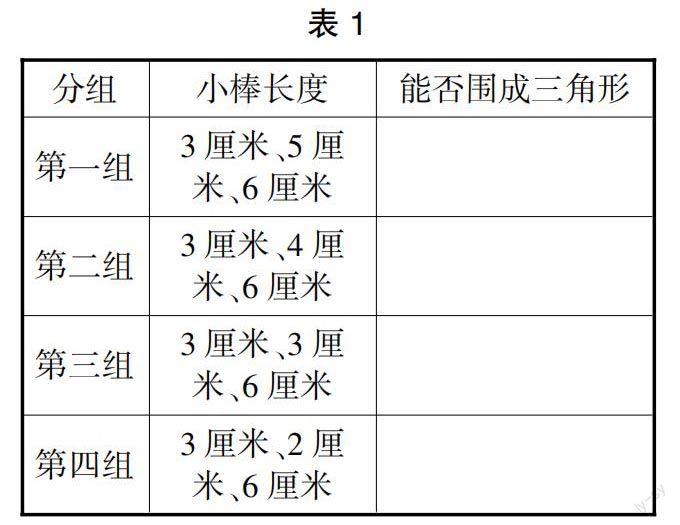
师：请同学们用（3厘米、5厘米、6厘米）（3厘米、4厘米、6厘米）（3厘米、3厘米、6厘米）（3厘米、2厘米、6厘米）这4组小棒进行实验操作，并完成下列表格。

（学生操作，教师巡回指导）

生1：我们小组发现第一组小棒可以围成三角形，第二组小棒也可以围成三角形，第三组小棒那两根3厘米的小棒跟那根6厘米的小棒“重合”了，因此无法围成三角形，第四组小棒也可以围成一个三角形。

生2：我们小组发现第四组小棒不能围成三角形。

师：为什么呢？

（学生展示）

生2：三角形是由三条线段首尾顺次相接围成的封闭图形，你们看，这两根小棒之间还有一点儿缝隙呢，这不能算是围成了三角形。

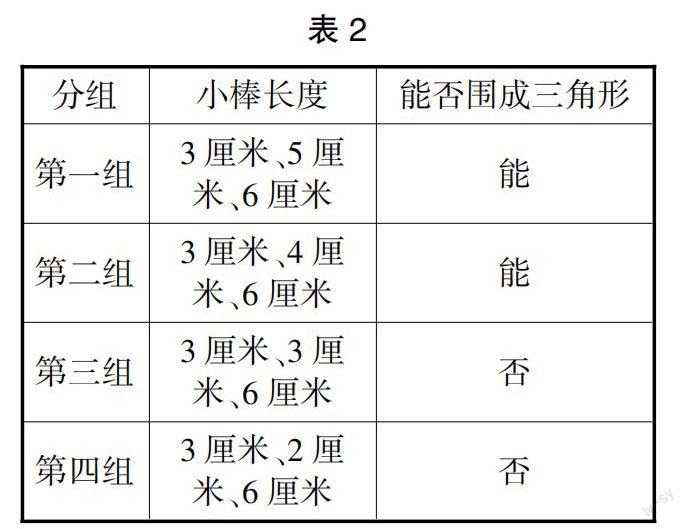
师：对，同学们在操作的时候一定要严密规范，只有这样才能得出可靠的结论。我把同学们的实验结果进行了汇总，请同学们看下面的表格。

实验是“做中学”的基本方式，动手操作是实验教学的重要环节。教学中，教师在实验开始前首先明确了实验目标，从而为实验操作提供了方向性指导。除此以外，教师依据实验目标引导学生填写表格，这就进一步理清了操作的步骤和思路。在实验过程中，教师指导学生从细节处着手，不但保证了实验结果的可靠性，还培养了学生严谨求实的作风。

[?]三、实验分析，结出真理的“硕果”

新课标指出，让学生经历观察、实验、猜想、证明等数学活动过程，发展合情推理能力和初步的演绎推理能力，能有条理地、清晰地阐述自己的观点。通过实验设计完成实验操作只是完成了数学实验的重要一步。在数学实验中，教师还应引导学生把思维聚焦于核心问题，使学生对实验结果进行数学化分析，用数学的眼光审视实验过程，用数学的语言分析实验过程，从而得出科学的实验结论[3]。

师：通过上面的实验操作，我们发现怎样的3根小棒才能围成一个三角形呢？

（学生讨论）

生3：我认为只要满足两根小棒长度之和大于第三根小棒的长度，那么这三根小棒就能围成三角形。

生4：我不同意。比如第四组小棒中，3+6>2，满足上述条件，可是不能围成三角形。

师：怎样能让我们的结论更加严谨呢？

生3：应该是任意两根小棒长度之和大于第三根小棒的长度，那么这3根小棒就能围成三角形。

生5：是的。当任意两根小棒长度之和等于或小于第三根小棒的长度时，这3根小棒就不能围成三角形。

师：我们如何理解“任意”两个字呢？

生3：我们以第二组小棒（3厘米、4厘米、6厘米）为例，“任意”的含义要求必须同时满足“3+4>6，3+6>4，4+6>3”这三个条件，才能得出这3根小棒能够围成三角形的结论。

师：对。通过上面的分析我们可以看出，如果我们要判断一组小棒是否满足“任意两根小棒长度之和大于第三根小棒的长度”会比较麻烦，同学们能想到什么好的办法吗？

（学生讨论）

生6：我认为只要满足“较短的两根小棒长度之和大于第三根小棒的长度”，就可以断定这3根小棒能够围成三角形。比如第二组小棒（3厘米、4厘米、6厘米），只需要判断出3+4>6，就可以得出这3根小棒能够围成三角形的结论。

生3：是的，这样再判断起来就变得简单多了。

师：通过能围成三角形的3根小棒的关系，我们得知，三角形任意两边之和大于第三边。如果三角形的兩条边分别是5厘米和8厘米，那么，第三条边的长度可能是多少厘米呢？（结果为整数）。请同学们以小组为单位进行分析。

生7：如果8厘米的边是最长的边，那么第三条边的长度应该大于8-5=3（厘米），如果最长的边是“第三条边”，那么第三条边的长度应该小于5+8=13（厘米）。所以，第三条边的长度应该介于3厘米到13厘米之间（不包括3厘米和13厘米）。

数学是锻炼学生思维的“体操”，数学实验是涵养学生思维的“能量场”。教学中，教师引导学生通过对实验数据进行分析，把4组小棒按照是否能够围成三角形进行归类，得出3根小棒能够围成三角形的内在规律。在这个过程中，教师指导学生用数学化的语言对实验结果进行表述，尤其是引导学生阐释“任意”二字，不但使学生获得了客观的数学结论，还充分体现了数学语言的严谨性。在学生充分理解实验结论的基础上，教师将“能够围成三角形”的讨论自然延伸到“三角形三边关系”的思考，并将这种思考进一步拓展，由此增加了学生对知识的深度理解。

德国戏剧家莱辛说：“对真理的追求比对真理的占有更为可贵。”实验探究的过程本质上就是追求真理的过程。教学中，教师引导学生把数学“做”出来，不但能够使学生获得对数学知识的积极情感体验，而且能够让学生在实验探究中掌握基本的数学知识和技能，锻炼学生的操作能力和思维能力，使学生获得解决问题的基本经验。

参考文献：

[1]  王亚. 开展数学实验，提高教学的适切性——以苏教版小学数学四年级《多边形的内角和》一课教学为例[J].小学教学参考，2021（21）：10-11.

[2]  谭婧. 小学“三角形三边关系”的教材分析与教学内容重构[D].广州大学，2018.

[3]  虞文辉. 从“三角形边的关系”一课看小学数学教学的发展[J]. 小学教学（数学版），2011（09）：8-9.