安哥拉独门沙画艺术:一笔画
张羿

在今天安哥拉东北部一个叫隆达(Lunda)的地方,生活着一个神秘的族群。大约在1600年前,这个族群迁徙到安哥拉,以流入赞比西河的隆圭本古(Lungwe-Bungo)支流的名字给自己取了名字——绍奎人(Chokwe)。根据绍奎人的传统,妇女从事农业生产,男人外出狩猎。工匠们忙于炼铁、绘画、雕塑、制作家具、编织垫子篮子。他们的艺术水平高度完美。此外,他们还拥有一门独特的沙画艺术——索纳(Sona)。
当绍奎人在村庄里或狩猎营地聚会时,他们围坐在篝火旁边或枝繁叶茂的树荫下,一边讲故事,一边在沙地上画画。这些沙画即是“索纳”。它是一种古老的传统,它描绘的是谚语、寓言、游戏、谜语、动物等。在知识和智慧代代相传的过程中,索纳发挥着重要作用。
男孩在学校接受教育期间,就会学习简单的索纳画法和意义。更难的索纳只有那些说书人知道,他们是真正的索纳画家。这些画家会把关于索纳的画法技术传给他们的男性后代。在绍奎人的社会中,他们很受尊敬,属于绍奎社会的精英阶层。
为了便于记忆标准化的沙画,索纳画家首先用手指在沙地上等距地戳洞,形成点阵,如图1。
接着,画家会绕着这些点画线,最终形成图案。通常情况下,图形是由一条或多条线组成的,这些线会把每个点都包围起来。图2展示了画线的过程。
点阵的行列数以及画线的规则都取决于要表现的主题。画家们只需记住点阵的行列数和画线的规则就能快速完成一幅索纳作品。旁观者会认为磕磕绊绊是才疏学浅的表现,所以画家们会一气呵成完成画作。如果图案比较复杂,画家会聚精会神,一言不发。但是,如果它相对简单,画家就一边画画一边讲故事。作品在沙子上画好之后,一般都会被擦掉。
到了19世纪,随着西方殖民者的入侵,索纳技艺逐渐衰落。许多人都只知道比较简单的图案,更复杂的图案的秘密只有一些年长的索纳画家了解。幸好,一些传教士和民族学家历尽千辛万苦收集索纳,这项珍贵的文化遗产才得以不至失传。
接下来,我们一边聆听“狮子和男孩”与“公鸡和豺狼”两个故事,一边欣赏绍奎人的索纳沙画艺术。
故事1:狮子和男孩
一个男孩和一头狮子是好朋友,他们从小一起长大,一直以打猎为生。有一天,轮到男孩去打猎了,但他不幸受伤晕倒。狮子立刻生起火,用一剂药救活男孩。他们带着猎物回家,举办了一场盛大的宴会,此后,他们的友谊更加牢固了。
过了一段时间,轮到狮子去打猎,在猎杀水牛的时候,狮子假装晕倒在地。男孩以为狮子已经死了,他突然想到,如果把狮子的眼睛、鼻子和耳朵制作成护身符,他就可以成为这个地区最著名的猎人。当男孩试图肢解狮子时,狮子突然一跃而起,杀死了背叛自己的朋友。
从那以后,再没人看到狮子和男孩这两大猎手在一起。
在索纳沙画中,狮子和男孩由两个较大的圆点代表。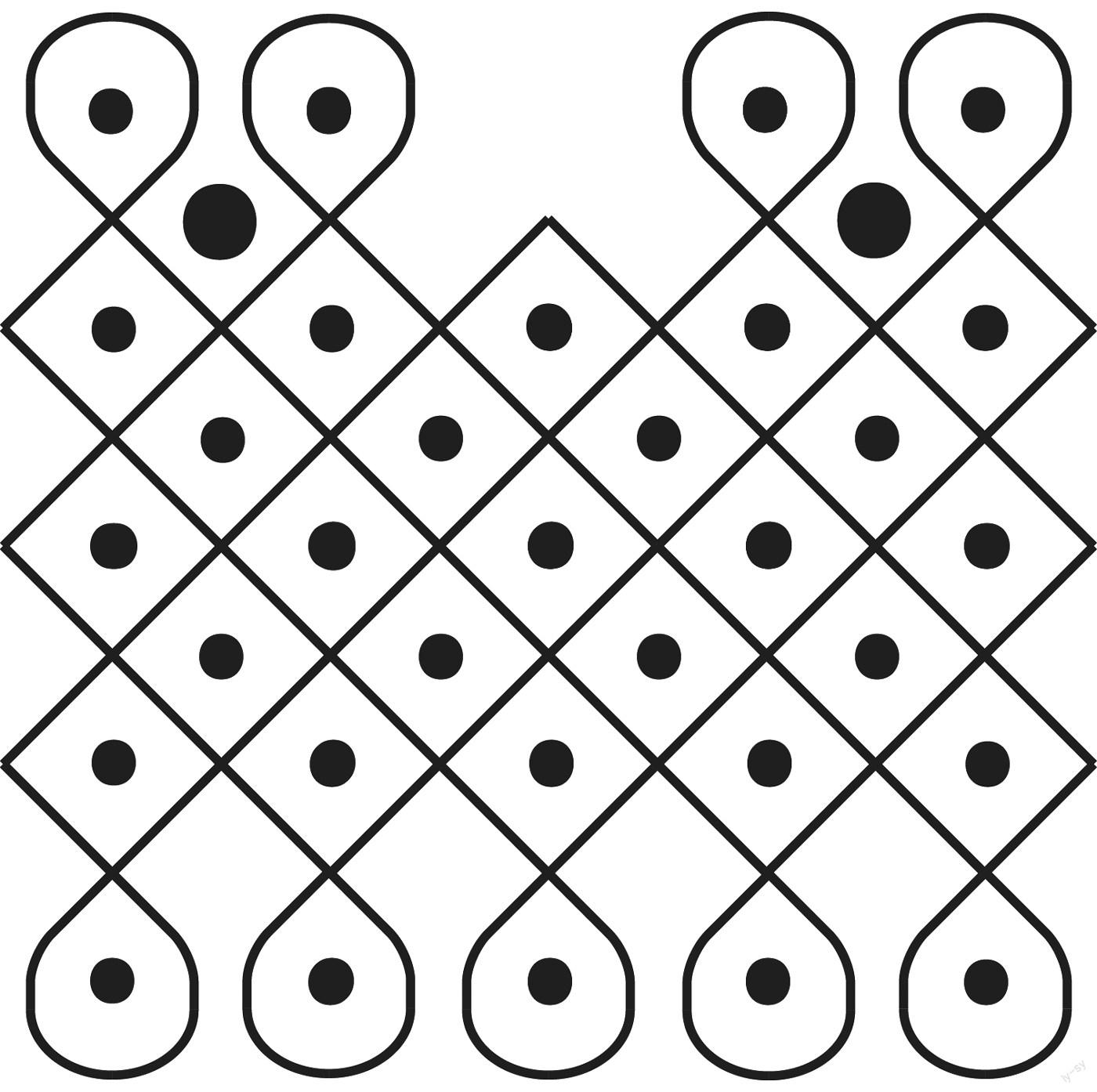
故事2:公鸡和豺狼
公鸡和豺狼想娶同一个女孩,于是他们都向女孩的父亲提亲。那父亲要求提前支付彩礼,公鸡和豺狼都表示同意,并立刻送上彩礼。突然,有传言说那女孩死了。公鸡痛哭不已,而豺狼只是懊悔自己的彩礼打了水漂。原来,这是女孩的父亲故意散布谣言,看谁配得上他女儿,最后他把女儿嫁给了诚意十足的公鸡。
在索纳沙画中,上面两个大点分别代表公鸡和豺狼。下方的大点代表女孩。
观察以上两幅索纳作品,我们大致可以发现以下3个特点:
1. 点阵中的每一个点都被线条分隔包围。这显而易见。
2. 整体图案是对称的。这同样显而易见。据统计,超过80%的索纳是对称的,有一条或多条对称轴的索纳出现的频率很高,这表明轴对称在绍奎人的民族文化中的重要性。
3. 整体图案是单线性,即一笔画出来的。这并不显而易见。据统计,大约75%的索纳是单线性的,这条线可以与自己相交,但永远不能重复自己走过的路径。你可能会问,如何一笔画出上面的索纳图案?这个问题恐怕并不简单。事实上,关于这类一笔画问题,大数学家欧拉曾经给出过答案。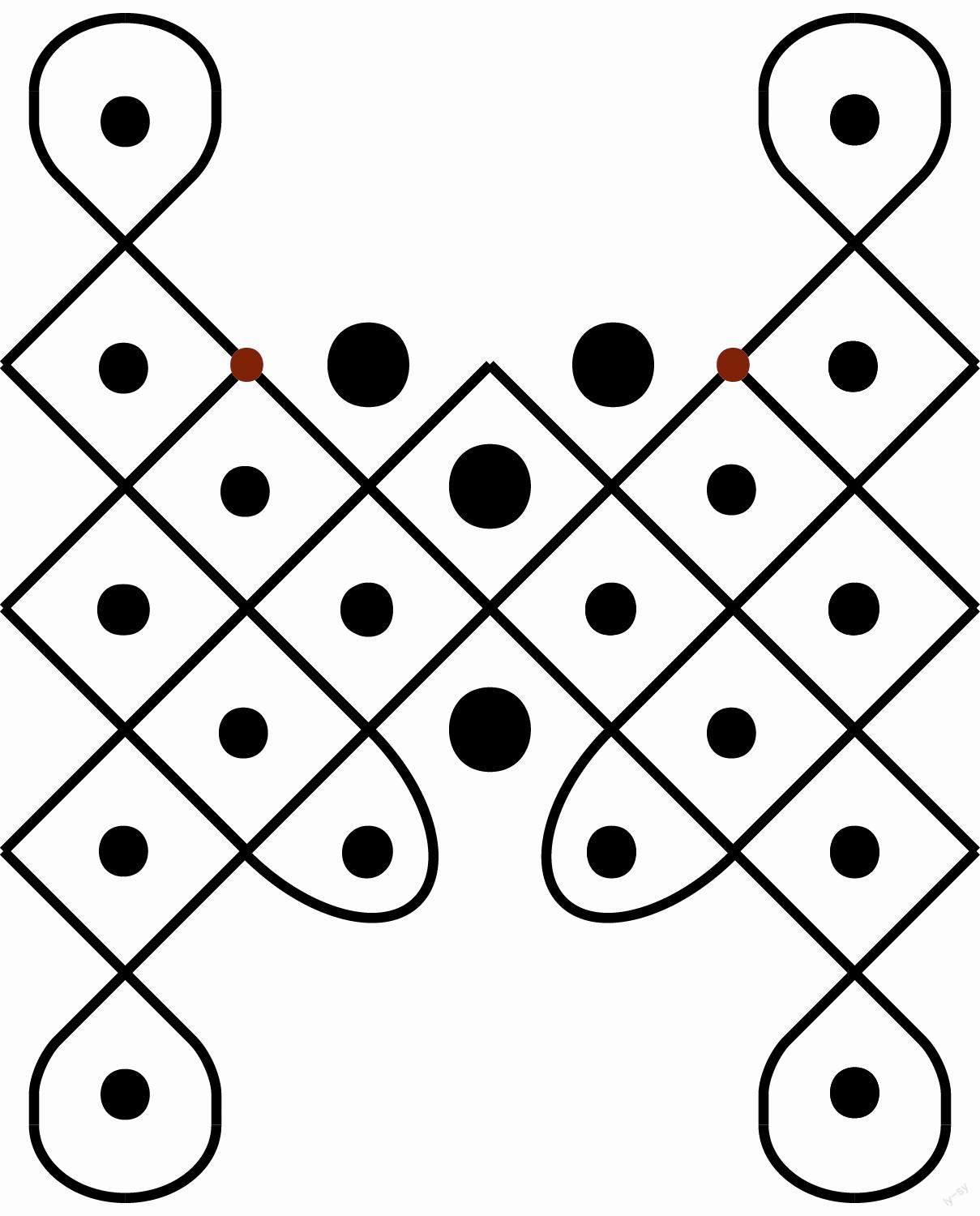
哥尼斯堡是中世纪德国的一座城市,城市建筑分布在普雷格尔河两岸,河流中间有两座岛,两岸和两岛之间有七座桥连接,如图5。当时哥尼斯堡的市长闲来无事研究一个问题,如何一次性通过这七座桥,既不能重复也不能落下。当时,人们的解法简单粗暴——只要把所有走法都画出来不就知道了嘛。市长觉得这种解法并不能让人满意,于是向著名数学家欧拉求助。
欧拉敏锐地发现这里蕴藏着深刻的数学内涵,并把它称为一笔画问题。欧拉表示:“把所有走法都列举出来的解法没有任何新意,用这种方法也许可以做出答案,但是到头来依然搞不懂问题的本质。”
欧拉的解法是,把两岸和两岛简化成四个“顶点”,把七座桥简化成七条边。于是,如图6,这四个顶点连接的边的数量分别是3、3、3、5。此時,问题随之转化成:能否一笔把图6这个图形画出来。经过思考,欧拉确认这是不可能的。同时,他还得出了任意一个图形是否可以一笔画的条件。首先,图形中的顶点分为两种,如果经过该点的线段数目是偶数,就称之为偶点;如果经过该点的线段数目是奇数,就称之为奇点。欧拉指出,如果一个图形可以一笔画,那么它的奇点个数只能是0个或2个。如果奇点个数是0个,那么从图形中任意一点出发,都可以一笔画;如果奇点个数是2个,那么只能从一个奇点出发,画到另一个奇点结束。
你可以用欧拉的方法尝试一下能不能一笔写成“口”“日”“目”三个字。“口”字的四个顶点全是边数为2的偶点,不存在奇点,所以你从任意一点起笔就能一笔写成。“日”字中间一横的两端有两个边数为3的奇点,所以你可以从其中一个奇点起笔,写到另一个奇点结束。“目”字的中间有两横,形成了4个边数为3的奇点,你无论怎么写都不能一笔写成。
现在再来看图6,所有4个顶点全是奇点。所以不管怎么画,都无法一笔画成。因为在绘画过程中一定会遇到一种情况,当你经过一座桥到达某个位置后,然后发现这个位置连接的另外两座桥都已经走过了,不重复就走不出去,所以这个问题是无解的。
后来,“二战”爆发,哥尼斯堡七桥中的两座桥毁于战火,只剩下了五座,如图7。所以,哥尼斯堡七桥今天已经不存在了。不仅七桥不存在,连哥尼斯堡也不存在了。1945年哥尼斯堡战役后,苏联红军占领了这座城市。战后它成为苏联领土,更名为加里宁格勒。如今,这里是俄罗斯的一部分,是俄军波罗的海舰队基地。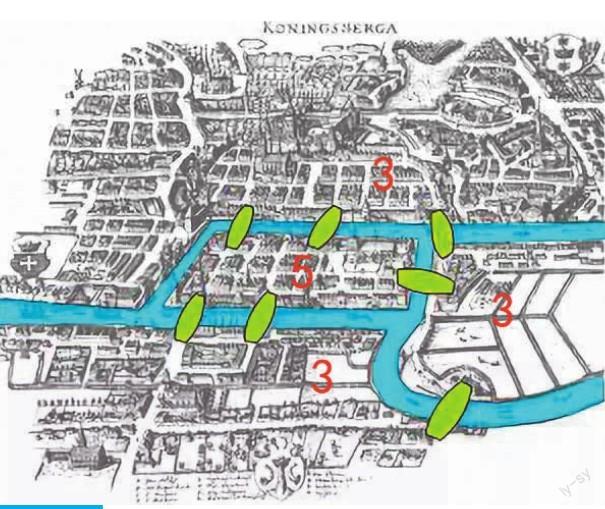
不过,如果你现在去那座城市,倒是可以一次不重复地走过五座桥了。如图7,四个顶点连接的边的数量分别是2、2、3、3。图8是五桥的等效图,你只需要从其中一个边数为3的顶点出发,就一定能不重复地走过五座桥,最终走到另一个边数为3的顶点结束。
欧拉这种用顶点和边解决问题的方式到后来发展成为一个数学概念“图论”。其中“图”就是画面整体,“顶点”代表对象,也就是岸和岛,“边”代表对象之间的关系,也就是桥。七桥问题的图里只有4个顶点,7条边。但在今天借助计算机,我们可以画出上万亿个“顶点和边”的图,把它作为数据来计算,这就是“图计算技术”。通过不断发展完善,图计算技术已经是世界前沿的数据技术,应用非常广泛。例如电网,全国一共有上亿台供电设备,一旦其中一台设备出问题,可能就会影响其他设备,出现大面积停电事故。所以可以把每个供电设备作为一个“顶点”,绘制出它们之间的关系图,建立起一个数据库,然后用这些数据进行预演,模拟关掉其中一个会对其他设备产生什么影响,这样在每次维护供电设备之前都可以提前预判,不影响正常供电。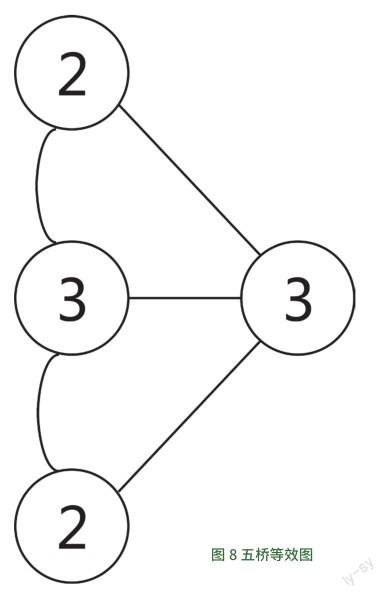
时至今日,中国已经成为世界上“大规模图计算技术”技术性能最高、应用最广泛的国家。而这一切其实都起源于哥尼斯堡那道简单的数学题。
言归正传,现在再看前文中安哥拉大叔“狮子和男孩”“公鸡和豺狼”两幅索纳沙画作品,相信你很容易就能确定它们都可以一笔画出来。狮子和男孩中所有顶点都是偶点,所以从任意一个顶点开始就能一笔画出这个图案;公鸡和豺狼中有两个顶点是奇点(即图4中的两个红点),其余都是偶点,那么一定可以从其中一個红点出发,到另一个红点结束。
图9的几幅索纳沙画作品锤子、小鸟、蝎子、山羊都是一笔画成的,读者可以自行尝试。

