基于SHPB试验的多尺寸大理岩动态力学性能研究

郭鹏飞 李志康 彭岩岩 张海江

(绍兴文理学院土木工程学院,浙江 绍兴 312000)

1914年,HOPKINSON提出了用霍普金森杆装置研究炸药爆炸或子弹射击杆端时的压力—时间关系[1]。在SHPB试验中,由于杆的材料、直径和撞击速度不同,试样的尺寸效应会受到特定杆径的影响。早在1939年,WEIBULL对岩石材料的尺寸效应进行了系统分析后,工程领域的学者对尺寸效应进行了大量研究[2]。HUDSON等[3]首次基于不同尺寸大理岩的单轴压缩试验结果,得出强度随岩样长径比变化而变化,显示出其具有尺寸效应。近年来,国内外学者利用霍普金森杆对大理岩进行了深入研究并取得了显著进展。李地元等[4]研究了含预制裂隙大理岩的动态力学性能,结果表明:岩石的能量吸收率随预制裂隙角的增大呈现先增大后减小的趋势,当端部裂隙与端面成适当角度时,会使能量吸收率达到最大,可有效提高破岩效率。高富强等[5]利用MTS和SHPB装置,对不同长径比的石灰岩进行了准静态和动态的冲击压缩试验,结果表明:长径比较小时,动态强度随石灰岩长径比的增大而减小,与静态试验结果一致;长径比较大时,动态强度随石灰岩长径比的增大而增大,长径比的临界值为0.5。杜晶[6]利用不同长径比的砂岩进行冲击试验,结果表明:长径比为0.4、0.5、0.6、0.8和1.0的砂岩动态强度随长径比的增加而增大,与静载条件下岩石强度的尺寸效应相反。DAVIES等[7]的研究结果表明:惯性效应为0时,试样的长径比约为(μ为试样泊松比),为使冲击试验中惯性效应和端部效应达到最小,试样长径比应控制在0.5左右。凌天龙等[8]对砂岩进行了三轴压缩试验和单轴SHPB冲击试验,分别得到了砂岩极限面参数、率效应参数、压力参数和损伤模型参数的取值,并基于得到的HJC模型参数利用有限元程序LSDYNA对粉砂岩SHPB冲击试验进行了数值模拟,结果表明:试验和模拟的应力—应变曲线形态吻合较好,验证了HJC模型参数试验测定方法的合理性和有效性。方秦等[9]基于三轴围压试验、Hugoniot试验和Hopkinson压杆试验数据,分别得到了Salem石灰岩极限面参数、压力参数和率效应参数取值,并基于得到的HJC模型参数利用有限元程序LS-DYNA对Salem石灰岩进行了数值模拟,计算结果与试验数据对比表明了所提出的HJC本构模型参数确定方法的合理性和有效性;此外,该项研究还对一般岩石材料HJC模型参数的确定给出了建议方法。现阶段,学术界的研究重点是对石灰岩、砂岩、花岗岩、混凝土、碳钢等试样的动态尺寸效应研究[10],对卸荷损伤大理岩的静、动力学性能研究[11],对不同高温大理岩在不同加载速率下的冲击压缩试验研究[12],对不同尺寸大理岩在不同加载速率下的动态拉伸试验研究[13]等。

大理岩在世界各地分布很广,常被应用于建筑工程、水利水电工程、水库等工程领域,是一种变质岩,又称大理石,是三大类岩石之一[14-15]。变质岩与其他两类岩石的成因、矿物成分、结构、构造、产状、分布都不相同,尤其是它们的动态力学性能存在较大差异[16-18]。本研究通过试验分析和理论分析法,以《岩石动力特性试验规程》(T/CSRME 001—2019)和《岩石材料动态单轴压缩强度测试方法》(T/CSEB 0004—2018),以及应力均匀性假设及一维应力波理论等为基础,基于SHPB试验,对多尺寸大理岩的动态力学性能进行详细分析。

1 SHPB试验

1.1 SHPB试验装置

本研究采用霍普金森杆装置进行冲击压缩试验,装置结构如图1所示。压杆材料为60Si2Mn,发射管、入射杆、透射杆、吸收杆及子弹型号规格分别为ϕ105 mm×2 000 mm、ϕ75 mm×5 000 mm、ϕ75 mm×3 000 mm、ϕ75 mm×1 000 mm、ϕ75 mm×600 mm。 通过设定空气炮的气压值控制子弹撞击入射杆的速度,气压值越高,弹速越大,杆对试样的冲击荷载越大。

1.2 试样制备及其力学参数

采用的试样来自湖南浏阳某加工厂,其端面不平行度和不垂直度为0.01～0.02 mm,符合国际岩石力学学会的基本要求。采用细颗粒大理岩精雕成ϕ50 mm×100 mm的标准圆柱形试样,利用高刚性岩石力学测试系统(MTS815.04)并采用速度为0.001 mm/s的连续位移控制加载模式对大理岩进行单轴压缩试验,测定的物理力学参数见表1,静态应力—应变曲线如图2所示。

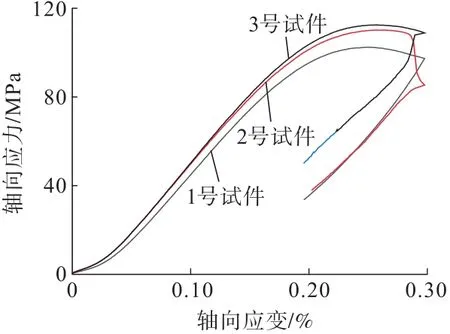
图2 大理岩试样静态应力—应变曲线Fig.2 Static stress-strain curves of marble specimens

表1 大理岩基本物理力学参数Table 1 Basic physical and mechanical parameters of marble

2 ANSYS/LS-DYNA数值模拟

2.1 材料模型与参数选择

2.1.1 钢的本构模型

子弹、入射杆和透射杆均采用钢材料参数的线弹性模型[19],参数密度ρ=7 800 kg/m3,弹性模量E=200 GPa,泊松比υ=0.3。

2.1.2 大理岩的动态本构模型

大理岩采用 Holmquist-Johnson-Cook(HJC)模型[20]进行分析。HJC模型包含极限面参数A、B、N和Smax,损伤参数D1、D2、EFMIN和率效应系数C,压力参数K1、K2、K3、pc、μc、pl和μl以及基本力学参数fc、G、T和ρ0共19个参数[9];EFMIN为材料断裂时的最小塑性应变,用来控制拉伸应力波导致的材料脆性开裂;SFMAX为材料所能达到的最大特征化等效应力。

目前关于类岩石材料冲击爆炸问题的数值模拟研究中[21-22],HJC模型的极限面参数较多地取与原始文献[20]相同的数值,即A=0.79、B=1.60、N=0.61,故本研究模拟中采用的HJC模型极限面参数(A、B、N)与之相同。 HOLMQUIST等[20]假定损伤参数与混凝土强度无关,由于缺少试验数值,故模拟中采用的HJC模型损伤参数与原始文献[20]相同,即D1=0.04、D2=1.0。根据凌天龙等[8]提出的确定砂岩HJC模型参数的理论和方法及方秦等[9]对一般岩石材料HJC模型的参数确定给出的建议方法,本研究通过试验数据拟合得到HJC模型其他参数取值。模拟中采用的HJC本构模型主要参数取值见表2。

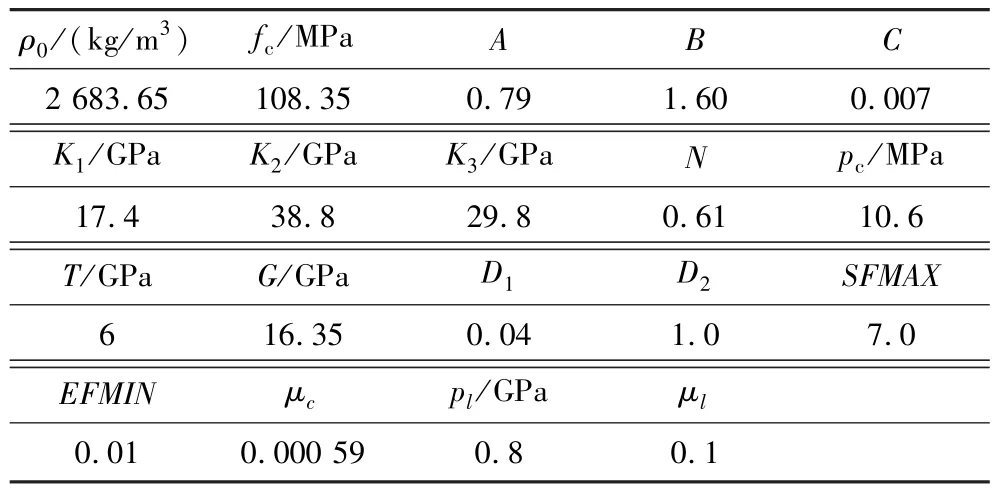
表2 HJC动态本构模型主要参数Table 2 Main parameters of HJC dynamic constitutive model

2.2 有限元模型构建

本研究采用有限元软件ANSYS/LS-DYNA,依据实验室中霍普金森杆的尺寸建立有限元模型。模型共分为子弹、入射杆、试样和透射杆4个部分,各部分均采用三维实体单元(Solid 164)。试样尺寸分别为ϕ50 mm×5 mm、ϕ50 mm×15 mm、ϕ50 mm×25 mm、ϕ50 mm×35 mm、ϕ50 mm×45 mm、ϕ70 mm×35 mm、ϕ60mm×30mm、ϕ50mm×25mm,试样尺寸及编号如表3所示。子弹、入射杆和透射杆径向均划分16份网格,子弹轴向划分30份网格,输入杆轴向划分250份网格,输出杆轴向划分150份网格。为了更准确地体现模拟结果,将试样网格进行了精细划分[23],试样径向划分32份网格,轴向划分6份网格,一共划分了16 134个网格;接触面之间均选择自动面面接触类型,失效应变设置为0.15,求解时间为5 ms,设置沿X方向的加载速度为 4、6、8、10m/s,模拟中试样的应力和应变取自其中心位置的应力和应变。以试样尺寸ϕ50 mm×25 mm为例,构建的有限元模型如图3所示,有限元分析流程如图4所示。图4中模型优化参数调整是针对冲击效果较不理想的试验,多次调整并优化HJC动态本构模型参数。

表3 试样尺寸及编号Table 3 Sample size and number

图3 SHPB模型Fig.3 SHPB model

图4 有限元分析流程Fig.4 Flow of finite element analysis

3 数值模拟结果及分析

3.1 不同长径比大理岩试样模拟结果

对5组不同长径比的大理岩式样在10 m/s的冲击速度下进行冲击加载模拟,结果如表4和图5所示。

由表4及图5可知:大理岩试样长径比为0.1时,其峰值应变较低,冲击作用下试样具有一定的完整性,长径比为 0.3、0.5、0.7、0.9 时,其承受能力随厚度的增加而增强;冲击速度为10 m/s时,试样峰值应变随长径比的增加而增大,其动态强度随长径比的增加先增大后减小,长径比为0.5时,其动态强度最大。与文献[5]及文献[6]的研究结果相比,研究不同长径比试样对岩石动态强度的影响时,岩性或杆直径等因素会导致结论具有不一致性。

图5 不同长径比大理岩试样的力学参数曲线Fig.5 Mechanical parameter curves of the rock specimens with different length-diameter ratios

表4 SHPB冲击模拟结果Table 4 SHPB impact simulation results

3.2 不同直径大理岩试样模拟结果

根据大理岩尺寸规格从大到小的顺序,依次对试样进行了冲击速度由低到高的冲击模拟试验,结果见表5,大理岩试样的典型破坏特征如图6所示。

表5 SHPB冲击模拟结果Table 5 SHPB impact simulation results

图6 大理岩试样的冲击破坏形态Fig.6 Impact failure patterns of marble specimens

依据实验室中霍普金森杆应变片的位置,入射杆端应变片到试样端的距离为2 365 mm,透射杆端应变片到试样端的距离为834 mm,模拟中入射杆取近似其0.5倍位置的应力,透射杆取近似其0.28倍位置的应力,试样直径为50mm时,在10m/s的冲击速度下入射杆和透射杆的应力波形如图7所示。

图7 数值模拟得到的大理岩试样的应力波形Fig.7 Stress waveform obtained by numerical simulation of marble specimens

3.2.1 应力—应变曲线分析

大理岩试样的应力—应变曲线如图8所示。由图8可知:冲击速度为4 m/s时,试样的动态强度随其直径减小呈现增加的趋势。结合表5可知:冲击速度相同时,试样的应变率随其直径减小呈现增加的趋势,因此小直径的试样强度高是因为其应变率高。在4m/s的冲击速度作用下,大理岩试样的应力—应变曲线与静态应力—应变曲线相似,都出现回弹现象;采用矩形波加载,透射杆滤波振荡剧烈,故应力—应变曲线峰值前回弹振荡。

图8 大理岩试样的应力—应变曲线Fig.8 Stress-strain curves of marble specimens

大理岩试样的应力—时间曲线如图9所示。由图9(a)可知:冲击速度为6 m/s、试样直径为70 mm时,试样在 1 154.6μs时应力第 1次达到峰值134.11 MPa,随后以“折线”段形式下降,在1 349.84 μs时下降到近似0 MPa后出现一个暂时稳定的应力平台,在3 899.44μs时应力第2次达到峰值19.71 MPa,随即以“折线”段形式迅速下降到近似0 MPa;冲击速度为6 m/s、试样直径为 60 mm时,试样在1 199.95μs时应力第1次达到峰值178.92 MPa,随后以“折线”段形式下降,在1 349.84μs时下降到近似0 MPa后出现一个暂时稳定的应力平台,在3 359.90μs时应力第2次达到峰值21.28 MPa,随即以“折线”段形式迅速下降到近似0 MPa。由图9(b)可知:冲击速度为8 m/s、试样直径为70 mm时,试样在1 154.56μs时应力第1次达到峰值179.39 MPa,随后以“折线”段形式下降,在1 589.69μs时下降到近似0 MPa后出现一个暂时稳定的应力平台,在3 884.81μs时应力第2次达到峰值30.46 MPa,随即以“折线”段形式迅速下降到近似0MPa;冲击速度为8 m/s、试样直径为60 mm时,试样在1 049.80 μs时应力第1次达到峰值185.42 MPa,随后以“折线”段形式下降,1 289.95μs时下降到0MPa后出现一个暂时稳定的应力平台,在3 344.64μs时应力第2次达到峰值18.11 MPa,随即以“折线”段形式迅速下降到0 MPa。综上分析可知:较大尺寸的试样受到较低冲击速度后,第1次应力波使其发生局部破坏,未发生整体破坏,随后应力波在试件端面不断发射,当反射波与试样中受到的主应力方向相反时,反射波对试样有卸载作用,当它们方向相同时,反射波对试样有加载作用,因此出现图9中应力波动的过程,直至试样被整体破坏,应力波失去了反射介质。在冲击破坏过程中,试样受到压缩和拉伸作用。

图9 大理岩试样的应力—时间曲线Fig.9 Stress-time curves of marble specimens

3.2.2 动态力学参数分析

由峰值应力—试样直径曲线(图10)分析可知:冲击速度不变时,试样峰值应力随其直径的增加而减小。冲击速度为10 m/s时,试样直径对峰值应力的影响不大,即随着冲击速度的增加,试样直径对峰值应力的敏感性逐渐减弱;试样直径为50 mm时,冲击速度的变化对其峰值应力的影响较小,随着试样直径的增加,冲击速度的变化对其峰值应力的影响增大。

图10 模拟峰值应力—试样直径曲线Fig.10 Simulated peak stress-sample diameter curves

为验证模拟中大理岩峰值应力随其直径变化的规律,取3组同一长径比、不同直径的试样在相同气压下进行冲击试验,试样加持和实物图如图11所示。实测结果与模拟结果对比如图12所示。由图12可知:试验结果与模拟结果的变化规律具有一致性,但试验中试样的峰值应力略小于模拟中试样的峰值应力,这是因为采用相同速度冲击试样时,试验中的应力波在入射杆和透射杆中随时间衰减,且入射杆和透射杆端面难免会有缺陷,导致试样在试验中受到的应力减弱。

图11 试样安装图和实物图Fig.11 Sample holding diagram and physical diagram

图12 实测结果与模拟结果对比曲线Fig.12 Comparison of the curves between measured results and simulated results

3.2.3 冲击破坏过程分析

大理岩的尺寸效应也反映在破碎形态方面,室内试验和数值模拟结果均表明,冲击速度为4 m/s时,试样随其尺寸减小均呈现完整形状,冲击速度为6、8、10 m/s时,试样的破碎情况随其尺寸的减小变得更加严重。冲击速度为8 m/s时,直径为 70、60、50 mm的大理岩试样的最终破坏形态如图13所示;冲击速度为10 m/s时,直径为 70、60、50 mm的大理岩试样的最终破坏形态如图14所示。试样直径不变时,其破碎情况随冲击速度的增加变得更加严重,以直径50 mm的大理岩为例,其在冲击速度4、6、8、10 m/s时的最终破坏形态如图15所示。

图13 模拟中大理岩试样破坏特征Fig.13 Damage characteristics of marble specimens in simulation

图14 试验中大理岩破坏特征Fig.14 Damage characteristics of marble specimens during tests

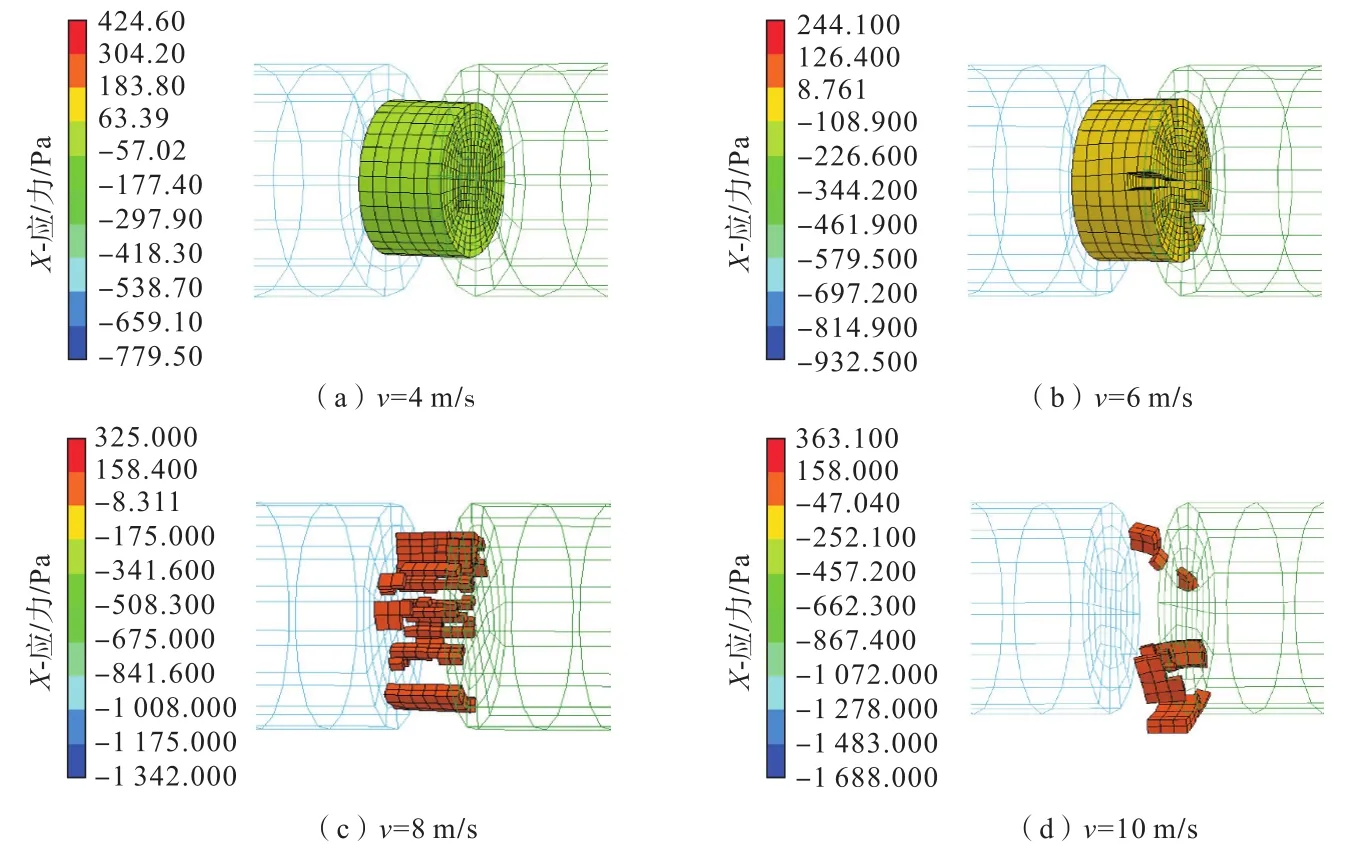
图15 ϕ50 mm的大理岩试样破碎形态Fig.15 ϕ50mm marble fragmentation pattern

由图16可知,冲击速度为6 m/s、试样直径为50 mm时,应力波在t=989.90μs时到达试样前端,t=3 239.90μs时试样前端内部产生宏观破坏带,t=3 659.90μs时试样的另一端产生宏观破坏带,此时试样前端萌生径向裂纹,t=4 034.80μs时试样内部出现轴向裂纹,t=5 000μs时试样呈现留芯形状,在冲击试验完成后,试样具有一定的完整性,只是发生局部破坏。由图17可知:冲击速度为10 m/s、试样直径为50 mm时,应力波在t=989.90μs时到达试样前端,t=1 259.90μs时试样萌生径向裂纹,并沿轴向方向贯通,t=2 519.90μs时试样沿轴向方向产生“十字型”裂纹,破碎为4块,并以“放射状”向试样周边破碎,t=4 095μs时试样已产生“爆裂式”破坏,t=5 000μs时试样最终呈现破碎式破坏。综上,在大理岩SHPB冲击试验中,试样的破坏形式以沿轴向方向的拉伸破坏为主。冲击速度较低时,试样仍保持一定的完整性(图16);当冲击速度较高时,试样破碎为无数碎屑(图17),试样破碎的数量取决于动力荷载。

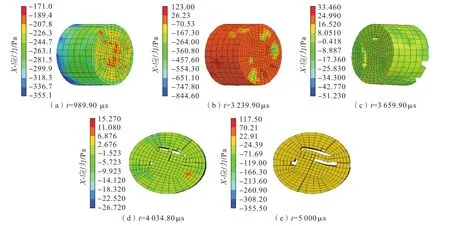
图16 大理岩冲击破坏动态变化过程(d=50 mm,v=6 m/s)Fig.16 Dynamic variation process of marble impact failure(d=50 mm,v=6m/s)

通过数值模拟发现,试样破坏与试样的应力峰值并不同步。由图9(a)可知,冲击速度6 m/s时,大理岩试样在989.90～1 289.90μs范围内应力处于峰值或在峰值点附近波动,但由图16可知:3 239.90μs时试样只是稍有破坏,4 034.80μs时破坏才加剧,试样的破坏滞后于应力峰值。由图9(c)可知:冲击速度为10 m/s时,大理岩在989.90～1 259.85μs范围内应力处于峰值或在峰值点附近波动,在1 034.96 μs时达到应力峰值,但由图 17可知:试样在1 034.96～1 259.90μs范围内发生损伤破坏,在2 519.90μs时发生剧烈破坏,试样的破坏稍微滞后于应力峰值。试样受到较低速度冲击时,其破坏所需要的应力较高,此时试样的破坏滞后于应力峰值,当试样受到较高速度冲击时,其破坏所需要的应力较小,此时试样的破坏稍微滞后于应力峰值。综上分析可知:冲击速度为 4、6、8、10 m/s时,试样的破坏滞后于应力峰值,滞后于应力峰值的时间随冲击速度的增加而减小。

图17 大理岩冲击破坏动态变化过程(d=50 mm,v=10 m/s)Fig.17 Dynamic variation process of marble impact failure(d=50 mm,v=10 m/s)

4 结 论

采用理论分析、数值模拟、室内试验等手段,验证了LS-DYNA中使用HJC本构模型研究大理岩冲击荷载作用下破坏过程、应力波形特征等的合理性,分析了大理岩力学参数随其尺寸变化的规律,确定了特定杆径下试样最优尺寸和最优冲击速度。本次数值模拟所采用的材料参数均按照实验室的SHPB装置参数设定,主要结论如下:

(1)室内实验和数值模拟结果均表明,大理岩的尺寸对SHPB试验结果中大理岩动态强度具有重要的影响。冲击速度不变时,大理岩动态强度随长径比的增大呈现出先增加后减小的趋势,随直径的增加而减小;试样直径不变时,大理岩动态强度随冲击速度的增加而增大。

(2)大理岩以沿轴向劈裂拉伸破坏为主,冲击速度不变时,其破坏形态随试样尺寸的减小变得破碎,试样尺寸不变时,其破坏形态随动力荷载的增大变得破碎。

(3)大理岩的破坏与应力峰值并不同步,试样的破坏滞后于应力峰值,滞后于应力峰值的时间随冲击速度的增加而减小。