细分解题方法 灵活应对高考

广东省吴川市第四中学 罗 亮 524500

2019 年高考讨论得最多的是数学试题出的难度太大，对于学生来说评价一道题难不难，很简单的，就是会做的就是简单题，不会做的、做不出来的都是难题.网络的声音有很多是学生发出来的，说明真的是有很多学生有题目不会做.本文只讨论其中一道题，就是最后的选做题22 题选修4-4 坐标系与参数方程这道题，因为本人教的一个学生平时的模拟考试中这个内容的题一般都是拿满分的，但是这次高考这道题就是做不出来，使得本人对这道题和这个内容进行反思.通过这道题目的解题分析，总结这一类题型的解题方法，反思教学中怎样总结解题方法和具体应用.

1 问题的呈现

思考：本题的解答过程看似简单，但是其第一问的参数方程化成直角坐标方程的思路难，为什么说它思路难呢？主要是同学们在备考的过程对这种思路接触得少，因为很多同学的思路都是加减消元，或是代入消元，很少用到这种平方后消元.因此无从下手，只能把直线l 的极坐标方程化成直角坐标方程，转化完成这道题就放弃了.那么，我们平时的教学中是否也存在问题？是不是我们没教好学生，导致学生不会做的呢？当然，学生考试不会做，肯定有我们老师的问题；因此，每次高考完了，我们要认真的反思我们的教学.

2 细分解题方法

这次高考结束了，我回头认真的翻看我们使用的教辅资料，并查看了市面上比较流行的教辅资料.发现一般的资料在参数方程这个内容的设置上，参数方程和普通方程的互化只设置一道例题，跟着变式练习就完了，就到下一个内容参数方程的应用了，所以在这个内容的复习上，我们老师讲授不多.我们总认为这个内容学生应该容易学，能处理好，这只是计算的问题而已.但这次的高考就有很多学生没能计算好，最终放弃这道题，而丢分，非常可惜.怎样教才能教会学生，使学生考试的时候能做好呢？用细分解题的方法.这个内容我们教学时间不多，要把解题的方法细分，帮助学生归纳总结，就要在我们讲一道例题时，把考试可能出现的方法都包括，然后总结出可能出现的解题方法.如：

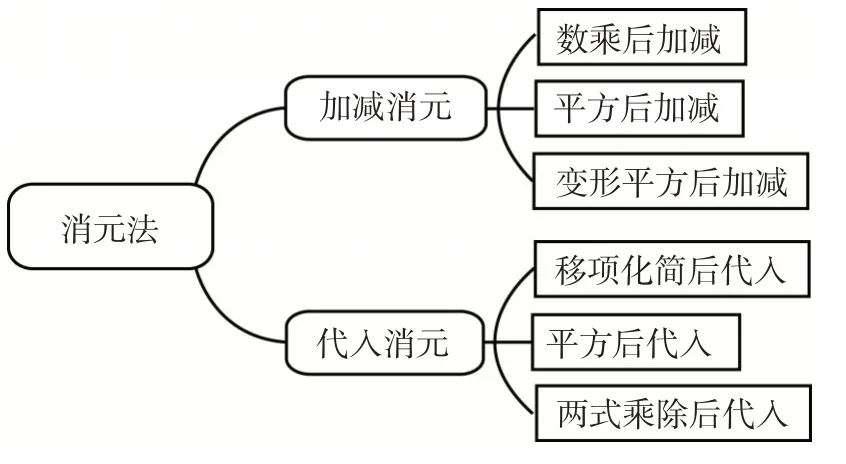
方法总结：上面参数方程化为普通方程的方法就是“消元法”，“消元法”再细分为“加减消元”和“代入消元”，“加减消元”再细分为“一个方程两边乘以一个常数再加上或减去另一方程”、“方程两边平方后相加或相减”和“先把方程变形后再方程两边平方后相加或相减”；“代入消元”再细分为“一个方程变形后代入另一方程”、“一个方程两边平方后代入另一方程”和“先把两方程相乘或相除变形后再代入”.简单的用下图表示：

3 总结方法的教学反思

对于参数方程化为普通方程的教学，大部分的老师都是简单的讲一道题，说明要把参数方程化为普通方程就是用“消元法”，就结束这个内容的讲解了.还有的老师这个内容都不专门讲例题了，就在模拟考试中出现的题目简单的讲解一下，说明是“消元法”就完了.因为这个“消元法”其实就是一种计算的问题，而计算问题在大部分数学老师的眼中是极为简单的问题，所以这种问题留给学生自己去感悟，自己去理解. 学生们在模拟考试中对于出现计算不难的问题都能做好了，也认为这个内容学会了，但一遇到难度加大的题目就会丢分.

对于总结方法的教学，不同的老师就有不同的看法：有老师认为数学方法靠的是感悟和理解，不用课堂上去归纳总结，让学生通过做题自己去感悟和理解；有的老师认为数学方法要一一的讲解，课堂上归纳总结出来，并尽可能的帮学生详细的总结.

谈到教学就一定要谈的是学生，因为教学是对学生进行的教学，不同的老师对总结方法的教学有不同的看法，主要是学生的不同.对于像“消元法”这种计算的问题的确是有的学生不用多讲，他们还能自己感悟出规律，考试也没有问题的，但这应该只是少部分同学. 因为中考计算要求越来越低，初中的计算公式把立方和（差）公式都删去了，只是有的学生参加数学竞赛对计算要求比较高，才有比较好的计算能力.大多数学生只针对中考学习的计算能力要求低，计算能力也跟着差.到了高中计算要求高了，像“消元法”也会有很多同学计算不出来，特别是学校里的“普通班”学生，这种“消元法”计算方法的教学还是要细分，要举例一一的讲解.现在提出的课堂教学是讲练相结合，并且有的学校还强制执行课堂上老师只能讲10 到15分钟，哪有这么多时间去讲解啊！办法总比困难多，我们给出练习让学生做，还可以让学生去讲，老师只需要总结一下，讲课的时间就多了. 总之，只要老师们意识到这种“简单的”计算问题也要细分解题方法，在课堂上总有办法解决，使“普通班”学生也能掌握好细分的解题方法，也能解决好这种计算的问题.

4 灵活应对高考

例1 的第一问就是参数方程化为普通方程，大部分学生都能想到“消元法”，就是不知怎样消去参数t，做不下去，而放弃这道题.其实这部分学生想到的“消元法”只是想到了“加减消元”和“代入消元”，没有想到再细分“加减消元”还有为“变形平方后消元”，如果想到这道题是可以拿下的.学生为什么想不到这个“变形平方后消元”法呢？本人也回想有教过学生这种方法吗？有，那是在讲《选修4—4：坐标系与参数方程》这本书的时候，讲课本第26 页练习第4 题的（3）、（4）小题（就是本文例2（2）、（3）小题），并且只是讲解这道题目要先把等式两边平方后（或把等式变形平方后）消元，讲完题目没有总结归纳出“变形平方后消元”法.并且到了高三复习，就没有再讲解过了，所以学生高考做不出来，也是正常的结果.

我们要做的就是让学生在考试中不再失分：首先，要让学生有解题的思路，思路就是从解题方法来，解题方法就是在课堂上的细分和归纳总结中想到；第二，要提高学生的计算能力，要提高学生计算的速度和准确度，确保学生会做的题目不失分；最后，回到本文提出的细分解题方法，在高考前要把重要题目出现过的方法细分整理出来给学生，让学生对解题方法有整体把握，加强考试信心，灵活应对高考.