基于TVF-EMD-PSO-GRU的月径流模型与应用研究

王秀杰，张 帅，田福昌，苑希民，曹鲁赣

基于TVF-EMD-PSO-GRU的月径流模型与应用研究

王秀杰1, 2，张 帅1, 2，田福昌1, 2，苑希民1, 2，曹鲁赣1, 2

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 天津大学建筑工程学院，天津 300072)

准确的径流预测在水资源规划和管理中发挥着重要作用．然而，受气候变化和人类活动等因素的影响，径流形成过程十分复杂，具有高度的非线性和非平稳性，更增加了径流预报的难度．为提高月径流预测精度，提出了基于时变滤波器的经验模态分解(TVF-EMD)和结合粒子群优化算法(PSO)的门限循环单元(GRU)的混合模型(TEPG)．首先利用TVF-EMD将原始月径流序列分解为若干个固有模态函数(IMF)，然后再利用PSO-GRU模型分别对每一个IMF进行预测，最后将每个IMF的预测结果相加得到原始月径流序列最终的预测结果．以黄河干流4个代表性水文站(包括唐乃亥站、头道拐站、花园口站、利津站)为研究对象，应用该模型对这4个测站的月径流进行单步预测研究，并与PSO-GRU(PG)模型、基于互补经验模态分解(CEEMD)的PSO-GRU(CPG)模型和基于经验模态分解(EMD)的PSO-GRU模型(EPG)进行对比分析．选用纳什效率系数NSE、相关系数、均方根误差RMSE、预报合格率QR及预报精度等级等评价指标对模型预测精度进行评价．结果表明，与PG模型、CPG模型、EPG模型相比，TEPG模型具有更高的预测精度和更好的泛化能力，4个水文站的NSE均达到0.981及以上，均达到0.992及以上，RMSE最大仅为64.031m3/s，QR均达到84.7%及以上，预报精度等级均为乙等及以上．因此，TEPG模型在预测非平稳和非线性月径流序列中具有较好的应用前景．

黄河流域；月径流预测；TVF-EMD；粒子群优化算法；门限循环单元

准确可靠的径流预报对水资源的配置管理和防洪减灾决策具有重要意义[1]．然而，受气候变化和人类活动等的影响，径流序列具有很强的非平稳性和非线性，增加了径流预报的难度．因此探索精度较高的径流预报方法成为水文预报领域亟待解决的问题．

径流预报的精度依赖于水文模型的构建，常用的水文模型包括集总式、分布式水文模型以及数据驱动模型．其中集总式水文模型预测精度较低，分布式水文模型不仅对水文数据的需求较高，而且需要建模者对流域物理机制有较详细的理解，所以在许多情况下，这两种模型无法对径流进行精度较高的预测[2].而数据驱动模型只需要从数据层面挖掘降雨、径流等水文变量间的相关关系，不需要深入理解流域水文循环的物理机制[3]．数据驱动模型包括数理统计模型和机器学习模型．其中，数理统计模型包括自回归滑动平均模型(ARMA)[4]、自回归综合移动平均模型(ARIMA)[5]、多元线性回归模型(MLR)等[6]，但是该模型需要待预测序列具有平稳性且服从高斯分布.由于降水、蒸发、下垫面变化和人类活动等不确定因素的影响[7]，径流序列通常具有非线性和非平稳性，因此该类模型的泛化能力较弱．而机器学习模型可以解决这个问题，因此在径流预报领域得到广泛应用．由于径流序列具有一定的趋势性、周期性和随机性特征，使用单一模型进行径流预测会导致原始径流序列中的部分重要信息遗漏[8]．因此探索基于多种信号分解技术的混合预测模型[9]成为了径流预测领域当前的研究热点．任博等[10]构建基于EMD-BPANN的年径流预测模型，并将其应用于凌河流域，获得了较高的预测精度．Wang等[11]将EEMD-ARIMA模型应用于年径流序列预测中．结果表明，与单一ARIMA模型相比，EEMD-ARIMA模型在中长期径流预报的精度上有很大提升．王栋等[12]将CEEMD与BP神经网络相结合进行月径流预测，并与EEMD-BP和单一BP神经网络模型对比，预测精度从高到低依次为CEEMD-BP、EEMD-BP、单一BP神经网络．包苑村等[13]提出了基于变分模态分解(VMD)的CNN-LSTM模型，并将其用于月径流预测，与其他模型相比，VMD-CNN-LSTM模型具有更高的预测精度．以上研究虽然提高了预测精度，但也存在一些不足，如EMD存在着端点效应和模态混叠的缺点[14]，EEMD虽然有效抑制了模态混叠，但是存在着残余的白噪声，导致重构误差大，分解完备性 差[15]．CEEMD在一定程度上抑制了模态混叠问题，但出现了伪分量，降低了模型的预测精度[16]．VMD虽然可以有效缓解信号的模态混叠，但是存在分解模态数的不确定性问题[13]．基于时变滤波器的经验模态分解(TVF-EMD)方法[17]有效改善了上述信号分解方法的弊端，如Zheng等[18]构建TVF-EMD-CQR-ORELM模型应用于短期风速预测，得到令人满意的预测结果；Song等[19]先采用TVF-EMD对广州市年降水进行分解，然后通过ENN模型进行预测，预报精度得到显著提升；王文川等[20]构建TVF-EMD-LSTM预测模型对长水水文站进行月径流预测．与其他模型相比，预测精度得到很大提升．

由于GRU具有良好的捕获时间序列中的长时间序列和短时间序列特征的能力，PSO可以自动寻找模型的最优参数，TVF-EMD可以有效减少模态混叠问题，因此本文提出TVF-EMD-PSO-GRU(简称TEPG)模型，将其应用于黄河流域唐乃亥、头道拐、花园口、利津4个水文站的月径流预测．

1 研究方法

本文主要介绍TVF-EMD信号分解方法和GRU网络的原理．常用的CEEMD、EMD信号分解方法及PSO优化算法的原理可以分别参考Yeh等[21]、Huang等[22]、Kennedy等[23]的文章，在此不再赘述．

1.1 TVF-EMD方法

Li等[17]于2017年提出了基于时变滤波器的经验模态分解(TVF-EMD)方法，该方法是一种自适应算法[24]，不需要人为确定参数．TVF-EMD的基本步骤如下．

(1) 给定一个原始信号()，通过EMD将()分解，得到若干个IMF和()的残差．

(2) 设(＝1，2，3，…)表示信号()的极大值点对应的时间序列．

(5) 构建B-spline近似滤波器进一步对()进行时变滤波，获得局部均值函数()．

1.2 门控循环单元

门控循环单元(GRU)[25]是对LSTM的改进，结构与LSTM类似，将LSTM的更新门和遗忘门整合为一个新的更新门机制，只采用更新门和重置门两个门控机制．与LSTM相比，在保证网络性能的前提下，结构更加简单，网络训练时间更短，大幅度提升了训练的效率．

GRU单元的具体结构如图1所示．图中和分别代表重置门、更新门．候选隐含状态的Sigmoid函数通常采用tanh/relu，将和的取值范围限定在[0，1]．

重置门为

更新门为

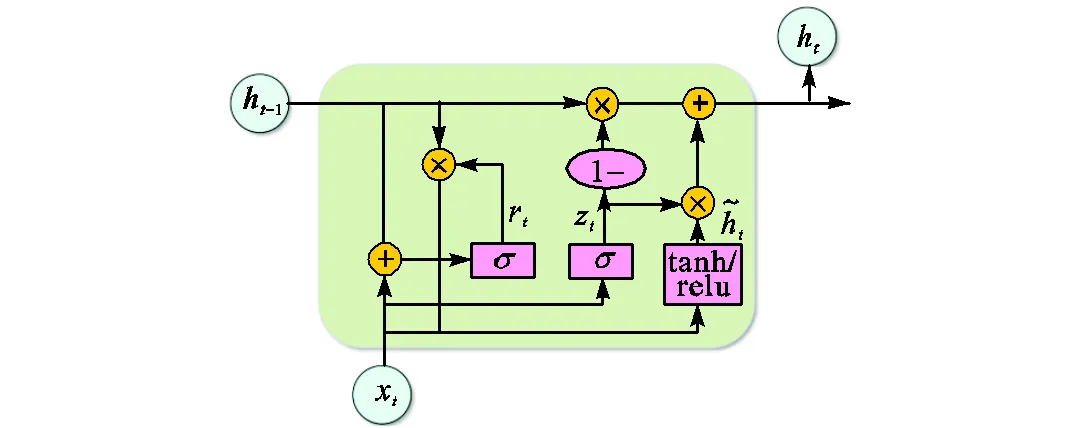
图1 GRU单元结构

1.3 TVF-EMD-PSO-GRU(TEPG)预测模型

人类活动和气候变化的影响，使水文时间序列具有非线性和非平稳性，尤其是月径流序列．为了更好地适应变化的径流过程以提升预报精度，本文提出了如图2所示的TVF-EMD-PSO-GRU(TEPG)混合预测模型架构．模型构建的具体步骤如下．

图2 TEPG预测模型研究思路

(1) 通过TVF-EMD将原始月径流序列分解为若干子序列．

(2) 将每个子序列划分为训练集和验证集，并对数据集进行归一化处理，使数据集处于[0，1]之间，以加快GRU网络的收敛速度．

(3) 通过搭建GRU网络来学习每个子序列中输入和输出变量之间的复杂关系．并通过粒子群优化算法(PSO)来自动确定GRU网络最优的学习率和隐含层节点数等．

(4) 使用训练好的GRU网络对子序列进行预测，将预测结果反归一化，以获得真实的预测值．

(5) 将每个子序列的预测结果相加，得到原始月径流序列的最终预测结果．

2 评价指标

本文采用纳什效率系数NSE、均方根误差RMSE、相关系数和《水文情报预报规范》(GB/T22482—2008)[26]中的预报合格率QR、预报精度等级等共5种评价指标来更加准确地对本文提出的TEPG模型的预测性能进行评定．

3 应用实例

黄河流域约位于95°53′E～119°05′E、32°10′N～42°50′N之间，总长度约5464km，东西方向长约为1900km，南北方向约为1100km，总流域面积约752443km2，是中国第二大长河．黄河源区是指黄河从河源至唐乃亥水文站之间的高寒草甸草原区，是黄河流域最重要的产流区．从河源至头道拐为黄河上游，河长3472km，流域面积为38.6万km2，多年平均降水量为396mm[27]．上游区是整个黄河流域的主要水资源供给区，由于降水补给以及少量冰川融水和地下水补给，上游区面积占黄河全流域面积的53.8%．从头道拐到花园口为黄河中游，干流长1234.6km，流域面积为34.4万km2．中游区地处黄土高原干旱、半干旱和半湿润气候区，多年平均降水量在520mm左右．天然年径流量约为120亿m3．从花园口到利津为黄河下游，由于黄河下游地势较低，水势平缓，泥沙量大，下游河段长期淤积形成举世闻名的“地上悬河”．

本文选取代表黄河不同气候和地理条件的4个水文站：唐乃亥、头道拐、花园口、利津．其中，唐乃亥站位于黄河源区，是黄河上第一个洪水编号站，也是国家重要水文站和黄河重点报汛站．头道拐站是黄河上游和中游的分界点，是黄河上游的出口站，也是中游万家寨水库的入口站．花园口站是黄河中游和下游的分界点，距离黄河源头约4700km，集水面积占黄河全流域面积的97%[28]．利津站作为黄河下游的最后一个水文站，控制着黄河入海的水沙量．图3为研究区域示意图．4个水文站的月平均流量数据来自黄河水利委员会和《黄河水资源公报》．所有数据均按照国家标准进行测量和检验，具有可靠性和真实性．本文选取唐乃亥水文站1956—2019年实测月径流序列和头道拐、花园口、利津水文站1950—2020年实测月径流序列对TEPG模型的预测性能进行检验．4个测站均选择月径流序列的前80%作为训练集，剩余的20%作为验证集．

3.1 TVF-EMD的分解结果

为解决径流的非平稳性问题，采用第1.1节所述的TVF-EMD方法分别对4个水文站的月径流序列进行分解．以唐乃亥水文站为例，对应的TVF-EMD分解结果如图4所示．由图可知，通过TVF-EMD分解，唐乃亥站原始月径流序列被分为了19个由高频到低频排列的IMF，每个IMF的周期性振荡变化特征较为明显，这有利于模型的训练和预测精度的提高．头道拐站、花园口站、利津站通过TVF-EMD分解得到的IMF数量分别为31、33、18．

3.2 模型构建与输入变量的确定

GRU网络预测性能的好坏取决于搭建网络的参数选择，如学习率、隐含层节点数、输入步长、隐含层个数、输出层节点数等．本文中，GRU网络的学习率和隐含层节点数由PSO进行自动寻优确定．以唐乃亥测站为例，每个IMF对应的GRU网络的最优学习率和最优隐含层节点数如表1所示．选用偏自相关函数(PACF)确定每一个IMF对应的GRU网络的输入步长．根据Feng等[29]介绍的输入选择方法，确定每一个IMF对应的GRU网络的输入步长．以唐乃亥水文站为例，各IMF对应的输入步长汇总于表2．由表2可知，每个IMF对应的GRU网络的输入步长不完全一致，这恰恰反映了月径流时间序列具有高度的不确定性和复杂性．隐含层个数设置为2层，输出层节点数等于预报值的个数，本文以月为单位，预报下一个月的径流，因此输出层节点数为1．为了验证TVF-EMD-PSO-GRU(TEPG)混合预测模型的优越性，在相同的预测流程下建立CEEMD-PSO-GRU (CPG)、EMD-PSO-GRU(EPG)和PSO-GRU(PG)模型进行对比分析．

图3 研究区域及水文测站位置图

图4 唐乃亥站1956—2019年月平均流量分解结果

表1 唐乃亥站各IMF对应的GRU模型最优参数

Tab.1 Optimal parameters of the GRU model corresponding to each IMF at the Tangnaihai station

表2 唐乃亥站各IMF对应的输入步长

Tab.2 Input steps corresponding to each IMF at the Tangnaihai station

3.3 预测结果与分析

将4个测站的月径流数据划分为训练集和验证集，用训练集的数据对各模型进行训练，用验证集的数据对预测结果进行对比验证，并选用NSE、RMSE、、QR、预报精度等级等5项评价指标对预测模型的精度进行评价．4个测站的验证集对比结果如图5所示．各项精度评价结果汇总于表3．由图5和表3可知，在PG、EPG、CPG、TEPG 4个模型中，TEPG模型在4个测站的5项评价指标的精度评价结果均为最佳．PG模型的预测效果最差，4个测站中NSE最高仅为0.661，最高仅为0.813，RMSE最大达到454.760m3/s．EPG模型的整体拟合效果以及峰值谷值处的拟合效果均低于CPG模型，其在4个测站的NSE均在0.717及以上，均在0.853及以上，RMSE最大达到295.916m3/s．CPG模型整体的拟合效果明显低于TEPG模型，在峰值谷值处的拟合效果略差，对应4个测站的NSE均在0.822及以上，均在0.914及以上，RMSE最大达到253.382m3/s. TEPG模型在4个测站的实测值与预测值曲线几乎完全拟合，尤其是峰值和谷值处．NSE均在0.981及以上，相对于CPG模型、EPG模型和PG模型在4个测站的NSE分别至少提高13.8%、25.1%、48.4%；均在0.992及以上，相对于CPG模型、EPG模型和PG模型在4个测站的分别至少提高4.8%、9.7%、22.0%；RMSE最大仅为64.031m3/s，相对于CPG模型、EPG模型和PG模型在4个测站的RMSE分别至少降低66.3%、73.8%、79.1%．TEPG模型在4个测站的QR均在84.7%及以上，预报精度等级均为乙等及以上．相对于CPG模型在4个测站的QR至少提高35.0%，相对于EPG模型在4个测站的QR至少提高97.3%，相对于PG模型在4个测站的QR至少提高了119.6%．

图5 各模型4个测站验证集结果对比

表3 4个测站不同模型的预测结果

Tab.3 Prediction results of different models of the four stations

分析比较4个模型在4个典型测站的预测结果可知，TVF-EMD能够提高频率分离性能和低采样率下的稳定性．同时对噪声的干扰具有鲁棒性．EMD方法虽然可以将隐藏在时间序列中的隐含信息自适应地分解为有限个IMF，但是容易产生模态混叠现象．CEEMD在EMD分解的基础上，通过向待分解的信号中加入正负成对的随机白噪声以达到与EEMD相当的分解效果，同时降低因白噪声引起的重构误差[21]，在一定程度上抑制了模态混叠，但是IMF依然包含残余噪声，因此在分解过程中产生较多的伪分量，增加模型的运行时间．此外，CEEMD和EMD两种分解方法还均存在着不具有时变特性、低采样率下分解性能较差的缺点[20]，从而降低了时间序列隐含信息的提取精度．可见TVF-EMD采用时变滤波器对待分解信号进行滤波处理以过滤掉某种随机成分，既保留了原序列的时变特性，又可以有效避免EMD和CEEMD分解中出现的模态混叠问题和CEEMD分解中出现的伪分量较多的问题．因此TEPG模型相比其他模型具有更好的预测性能．

通过对比TEPG模型在黄河流域4个代表性水文站的预测结果可知，唐乃亥水文站的各项评价指标结果在4个测站中均为最佳，这与唐乃亥水文站处于黄河源区、径流过程受人类活动等因素影响较弱有一定关系．而其他3个测站受到水库调蓄、水资源调度等因素影响较大，因此各项评价指标结果相对于唐乃亥站较差．

4 结 论

本文采用TVF-EMD、CEEMD、EMD 3种信号分解方法分别对黄河干流的唐乃亥、头道拐、花园口、利津4个测站的月径流序列进行分解，然后通过PSO-GRU模型进行单步预测．通过NSE、RMSE、、QR、预报精度等级等5个评价指标对模型预测精度进行分析比较，得出的结论如下．

(1) TEPG、CPG、EPG 3种混合模型的NSE、、RMSE、QR、预报精度等级均优于PG模型，由此可见，与直接采用原序列进行月径流预测相比，采用“分解-预测-重构”方法的预测精度更高．可见，信号分解方法能更好地识别月径流序列中的周期、趋势等本质特征，进而提高月径流模型的预测精度．

(2) 3种混合模型在4个测站的预测精度由高到低依次为：TEPG模型＞CPG模型＞EPG模型．TEPG模型相比于CPG模型和EPG模型具有更优的预测精度以及更低的误差．在4个测站的NSE均达到0.981及以上，均达到0.992及以上，RMSE最大仅为64.031m3/s．QR均达到84.7%及以上，预报精度等级均为乙等及以上．该模型不仅在整体上真实值与预测值的拟合效果最佳，而且在峰值谷值处的预测效果也较好，因此该模型具有稳定性和实用性，是一种提升中长期径流预测精度的很有前景的 方法．

(3) TVF-EMD能够有效减少信号分解中的模态混叠现象，对噪声的干扰具有较好的鲁棒性，同时擅于捕捉到低采样率下的信号，因此该方法的频率分离性能更佳，能够更好地将复杂的月径流序列分解为更加平稳的信号，进而得到更优的预测结果．

［1］ 高祥涛，李士进. 基于经验模态分解的水文时间序列预测研究[J]. 水文，2009，29(3)：66-68.

Gao Xiangtao，Li Shijin. Research on hydrological time series prediction based on empirical mode decomposition[J]. Journal of China Hydrology，2009，29(3)：66-68(in Chinese）.

［2］ Nayak P C，Sudheer K P，Rangan D M，et al. Short-term flood forecasting with a neurofuzzy model[J]. Water Resources Research，2005，41(4)：99-119.

［3］ Srinivasan K. Improved higher lead time river flow forecasts using sequential neural network with error updating [J]. Journal of Hydrology & Hydromechanics，2014，62(1)：60-74.

［4］ Valipour M，Banihabib M E，Behbahani S M R. Parameters estimate of autoregressive moving average and autoregressive integrated moving average models and compare their ability for inflow forecasting[J]. Journal of Mathematics and Statistics，2012，8(3)：330-338.

［5］ Valipour M，Banihabib M E，Behbahani S M R. Comparison of the ARMA，ARIMA，and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir[J]. Journal of  Hydrology，2013，476：433-441.

［6］ Adamowski J，Fung Chan H，Prasher S O，et al. Comparison of multiple linear and nonlinear regression，autoregressive integrated moving average，artificial neural network，and wavelet artificial neural network methods for urban water demand forecasting in Montreal，Canada[J]. Water Resources Research，2012，48(1)：273-279.

［7］ Jonathan B，Hatim S. An ensemble empirical mode fecomposition，self-organizing map，and linear genetic programming approach for forecasting river streamflow[J]. Water，2016，8(6)：247.

［8］ 邵 骏，袁 鹏，张文江，等. 基于贝叶斯框架的LS-SVM中长期径流预报模型研究[J]. 水力发电学报，2010，29(5)：180-184，191.

Shao Jun，Yuan Peng，Zhang Wenjiang，et al. Study of mid-long term runoff forecast based on LS-SVM in Bayesian evidence framework[J]. Journal of Hydroelectric Engineering，2010，29(5)：180-184，191(in Chinese).

［9］ Wu C L，Chau K W，Li Y S. Methods to improve neural network performance in daily flows prediction[J]. Journal of Hydrology，2009，372(1/2/3/4)：80-93.

［10］ 任 博，薛泽宇，任全志，等. 基于EMD的凌河流域降水径流预测模型研究[J]. 人民黄河，2016，38(6)：63-65.

Ren Bo，Xue Zeyu，Ren Quanzhi，et al. Rainfall runoff forecast application of BP prediction model based on EMD in Linghe river basin[J]. People’s Yellow River，2016，38(6)：63-65(in Chinese）.

［11］ Wang W，Chau K，Qiu L，et al. Improving forecasting accuracy of medium and long-term runoff using artificial neural network based on EEMD decomposition[J]. Environmental Research，2015，139：46-54.

［12］ 王 栋，魏加华，章四龙，等. 基于CEEMD-BP模型的水文时间序列月径流预测[J]. 北京师范大学学报(自然科学版)，2020，56(3)：376-386.

Wang Dong，Wei Jiahua，Zhang Silong，et al. Hydrological temporal series of monthly runoff prediction by CEEMD-BP model[J]. Journal of Beijing Normal University(Natural Science)，2020，56(3)：376-386(in Chinese).

［13］ 包苑村，解建仓，罗军刚. 基于VMD-CNN-LSTM模型的渭河流域月径流预测[J]. 西安理工大学学报，2021，37(1)：1-8.

Bao Yuancun，Xie Jiancang，Luo Jungang. Monthly runoff prediction of Weihe river basin based on VMD-CNN-LSTM model[J]. Journal of Xi’an University of Technology，2021，37(1)：1-8(in Chinese).

［14］ Naik J，Satapathy P，Dash P K. Short-term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression[J]. Applied Soft Computing，2018，70：1167-1188.

［15］ Zhang W，Qu Z，Zhang K，et al. A combined model based on CEEMDAN and modified flower pollination algorithm for wind speed forecasting[J]. Energy Conversion and Management，2017，136：439-451.

［16］ Wang X，Wang Y，Yuan P，et al. An adaptive daily runoff forecast model using VMD-LSTM-PSO hybrid approach[J]. Hydrological Sciences Journal，2021，66(9)：1488-1502.

［17］ Li H，Li Z，Mo W. A time varying filter approach for empirical mode decomposition[J]. Signal Processing，2017，138：146-158.

［18］ Zheng W，Peng X，Lu D，et al. Composite quantile regression extreme learning machine with feature selection for short-term wind speed forecasting：A new approach[J]. Energy Conversion and Management，2017，151：737-752.

［19］ Song C，Chen X. Performance comparison of machine learning models for annual precipitation prediction using different decomposition methods[J]. Remote Sensing，2021，13(5)：1018.

［20］ 王文川，高 畅，徐 雷. 基于TVF-EMD与LSTM神经网络耦合的月径流预测研究[J/OL]. 中国农村水利水电，http://kns.cnki.net/kcms/detail/42.1419.TV. 20210907.0938.004.html，2021-09-07.

Wang Wenchuan，Gao Chang，Xu Lei. Monthly runoff forecast based on TVF-EMD and LSTM neural network coupling[J/OL]. China Rural Water and Hydropower，http://kns.cnki.net/kcms/detail/42.1419.TV.20210907.0938.004.html，2021-09-07(in Chinese).

［21］ Yeh J R，Shieh J S，Huang N E. Complementary ensemble empirical mode decomposition：A novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis，2010，2(2)：135-156.

［22］ Huang N E，Shen Z，Long S R，et al. The empirical mode decomposition and the hilbert spectrum for nonlin-ear and non-stationary time series analysis[J]. Proceedings Mathematical Physical and Engineering Sciences，1998，454(1971)：903-995.

［23］ Kennedy J，Eberhart R. Particle swarm optimization [C]//Proceedings of ICNN'95-International Conference on Neural Networks. 1995，4：1942-1948.

［24］ Xu Y，Cai Z，Ding K. An enhanced bearing fault diagnosis method based on TVF-EMD and a high-order energy operator[J]. Measurement Science and Technol-ogy，2018，29(9)：095108.

［25］ Cho K，van Merriënboer B，Gulcehre C，et al. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation[EB/OL]. https:// arxiv.org/abs/1406.1078，2014-09-03.

［26］ GB/T 22482—2008 水文情报预报规范[S]. 北京：中国标准出版社，2009.

GB/T 22482—2008 Standard for Hydrological Informa-tion and Hydrological Forecasting[S]. Beijing：Standards Press of China，2009(in Chinese).

［27］ Li E，Mu X，Zhao G，et al. Multifractal detrended fluctuation analysis of streamflow in the yellow river basin，China[J]. Water，2015，7(4)：1670-1686.

［28］ Tang Y，Tang Q，Tian F，et al. Responses of natural runoff to recent climatic variations in the yellow river ba-sin，China[J]. Hydrology and Earth System Sciences，2013，17(11)：4471-4480.

［29］ Feng Z，Niu W，Tang Z，et al. Monthly runoff time series prediction by variational mode decomposition and support vector machine based on quantum-behaved particle swarm optimization[J]. Journal of Hydrology，2020，583：124627.

Monthly Runoff Model and Application Based onTVF-EMD-PSO-GRU

Wang Xiujie1, 2，Zhang Shuai1, 2，Tian Fuchang1, 2，Yuan Ximin1, 2， Cao Lugan1, 2

(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2. School of Civil Engineering，Tianjin University，Tianjin 300072，China)

Accurate runoff forecasting is important in water resources planning and management. However，because of the influence of climate change and human activities，the runoff formation process is very complex，with a high degree of nonlinearity and nonstationarity，making runoff forecasting challenging. A hybrid modelTEPGbased on time-varying-filter-based empirical mode decomposition(TVF-EMD)and gated recurrent unit(GRU)combined with particle swarm optimization(PSO)is proposed to improve the accuracy of monthly runoff forecasting. First，the original monthly runoff series is decomposed into several intrinsic mode functions(IMFs)by the TVF-EMD，and each IMF is subsequently predicted by the PSO-GRU(PG)model. Finally，the final prediction result of the original monthly runoff series is obtained by adding the prediction results of each IMF. The model was used to predict the monthly runoff of four representative hydrological stations in the mainstream of the Yellow River(including the Tangnaihai station，Toudaoguai station，Huayuankou station，and Lijin station)as the research object，and it was compared to the PG model，the complementary ensemble EMD(CEEMD)-based PG(CPG) model，and the EMD-based PG(EPG) model. To evaluate the prediction accuracy of the model，the evaluation indicators，including the Nash-Sutcliffe efficiency coefficient NSE，the correlation coefficient，the root mean square errorRMSE，the qualified rate of predictionQR，and the prediction accuracy grade，were selected. The results show that the TEPG model had higher prediction accuracy and better generalization ability than the PG，CPG，and EPG models. The four hydrological stations had an NSE of 0.981 and above，anof 0.992 and above，a maximum RMSE of only 64.031m3/s，a QR of 84.7% and above，and prediction accuracy of grade B and above. Therefore，the TEPG model has a good application prospect in predicting nonstationary and nonlinear monthly runoff series.

Yellow River basin；monthly runoff forecast；TVF-EMD；particle swarm optimization；gated recurrent unit

10.11784/tdxbz202108005

P333

A

0493-2137(2022)08-0802-09

2021-08-02；

2021-11-02.

王秀杰（1973—  ），女，博士，副教授，wangxiujie@tju.edu.cn.Email：m_bigm@tju.edu.cn

田福昌，tianfuchang@tju.edu.cn.

国家重点研发计划资助项目(2018YFC1508403)；科技部重点领域创新团队项目(2014RA031).

the National Key Research and Development Program of China(No. 2018YFC1508403)，the Innovation Team in Key Areas of the Ministry of Science and Technology(No. 2014RA031).

(责任编辑：樊素英)