接触式轮廓仪的测量精度问题

张穗，刘楠

（陕西工业职业技术学院，陕西咸阳，712000）

0 引言

轮廓仪[1]是对物体的轮廓、平面尺寸、平面位移进行检验的精密测量仪器。它由工作平台、探针、传感器等部件组成。在测量时探针接触测量工件并保持匀速滑行，同时传感器会感受到工件表面在X、Z方向的表面变化程度，将其转换成相应的电信号，进一步，电信号可转化为相应的数字信号。由于在实际测量中会存在探针缺陷、扫描位置不准等问题，使得测量工件的成图轮廓变得比较粗糙。为此，本文针对接触式轮廓仪的测量精度问题，建立了相应的数学模型求解被测工件轮廓线的各项参数，并利用仿射变换模型[2]对偏移数据进行了数据校正。这里，仿射变换是一种二维坐标到二维坐标之间的线性变换，可以保持二维图形的平直性和平行性，对于平面图像或者绕某一点旋转的图像都可以采用仿射变换模型。

1 工件1轮廓线各项参数的求解模型

1.1 轮廓标注

为使数据更直观的刻画出所测工件的外观轮廓，首先使用matlab软件[3-5]对附件一(level)中的数据分段进行平滑处理，然后利用处理后的数据描绘出工件1的大致轮廓线。假设被测工件的轮廓线都是由直线和圆弧构成的平面曲线，我们可以从轮廓线中找到拐点的大致位置。使用excel对直线L上的数据进行一元线性拟合，对曲线Q进行二次线性拟合，分别求出拐点G和切点q的位置坐标，最后利用计算得出的各拐点位置坐标可以计算以下参数的具体值。

(1)槽口宽度

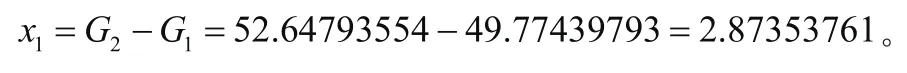
同理可得：x3=2.10645554,x5=2.09754545,x7=10.08752638,x11=7.36693841,x13=7.49205518。

(2)水平线段的长度

同 理 可 得：x4=4.95954545,x6=4.93051247,x8=2.97605155,x9=0.95845465,x10=4.89109929,x12=4.91693326。

(3)圆弧长度

由上所得数据，利用solidworks软件建立草图，并对草图进行相应的约束，再利用solidworks软件中的尺寸标注进行标注，得出圆心角n为63.29°，最后将圆心角n带入弧长公式中可以计算得到弧长

同理可得：Q2= 2 .1262,Q3= 2 .9334,Q4= 2 .0193,Q5= 2.0212,Q6= 1 0.8546,Q7= 1 2.4302。

(4)斜线线段的长度

根据上面所得数据，利用matlab软件编程计算得出斜线L2两端点间之间的距离等于3.0242. 同理可得：L3=2.8968,L5=2.0927,L6=2.8845,L8=1.5916,L9=3.0752,L11=5.1667,L12=5.3395。

(5)圆心之间的距离

已知圆上三点即可确定圆心。利用matlab求得圆心的位置坐标为O1(51.2199,-4.2672)、O2(58.4211,-4.2928).因此C1=O2-O1= 7 .2012 。

同理可得：C2=8.0126,C3=19.4337,C4=2.9422,C5=9.7631,C6=12.7056。

1.2 工件1的偏移角度与标注

由于附件一中的数据庞大而繁多，先用matlab软件对附件一中的数据进行一定的预处理，如剔除部分异常数据，使其便于观察分析，再将附件一中的数据导入matlab软件，进行图像绘制，可得工件大致轮廓图。进一步，使用matlab软件对附件一(down)中的数据进行可视化处理，剔除凹槽处的数据值。用余下的数据进行一元线性拟合，得到一条拟合直线y=-0.1308x+7.7876,该直线的斜率k=-0 .1308,利用公式

得到倾斜角θ= 7 .452°.

求得倾斜角之后，因工件需要水平放置，所以需要将工件的位置数据进行校正。我们可以使用matlab软件的仿射变换模型程序将工件轮廓进行水平校正，用水平校正后的位置数据计算出工件的各项参数值。结果如下所示：

(1)槽口宽度：x1=3.363,x3=2.4615,x5=2.2136，x7=10.4894，x11=4.5458，x13=7.5939。

(2)水平线段长度：x2=4.5978,x4=4.6689,x6=4.8745,x8=2.645,x9=0.9345,x10=7.7505,x12=5.1042。

(3)圆弧长度：Q1=0.56057,Q2=0.36271,Q3=0.946834。

(4)斜线与水平线之间的夹角：∠1=109.504°,∠2=110.415°,∠3=104.957°,∠4=108.672°,∠5=105.456°,∠6=106.192°,∠7=168.886°,∠8=168.767°。

(5)斜线线段的长度：L2=3.0295,L3=3.4167,L5=3.0644,L6=3.2401,L8=3.1059,L9=3.1551,L11=5.3862,L12=5.2889。

(6)人字形线的高度：z1=0.9889。

2 工件2轮廓线的各项参数值的求解

2.1 工件2的10次测量分析

利用matlab软件对附表二中工件2的10次测量数据进行平滑处理，使得数据变得可视化，方便我们分析并解决问题。

(1)偏移角

由1中方法求得工件2十次测量的倾斜角如下表1。

表1 工件2十次测量的倾斜角

(2)槽口宽度等参数

由于工件2在测量过程中有偏移，所以轮廓线也呈偏移的状态。因此，要求解槽口宽度等参数，我们需要对10次测量的数据进行校正。同样利用问题二中的仿射变换模型进行校正处理，然后借助模型一中求解各参数的模型，对本题的参数进行求解，结果如表2所示。

表2 各项参数值

(3)整体轮廓

对整体轮廓的分析，我们采用平滑处理及校正后的数据求均值的方法建立坐标模型，求出10组数据中的各相应点的位置坐标。即

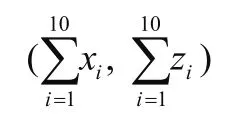
最后将求得的均值位置坐标导入matlab软件中生成整体轮廓图。

2.2 对工件2各项参数的校正处理

首先使用matlab软件处理附件3及附件4的数据，进行可视化处理，然后利用matlab软件的仿射变换模型对上述数据进行校正。这里由于关于圆和角的9次局部测量所得数据点比较密集，部分数据点重合，视图大小有限导致可视化后的9条轮廓线重叠为3条，分别计算关于圆和角的9次局部测量可视化后可见的3条轮廓线的各项参数值，最后求均值得出最终的参数值，如下表3所示。

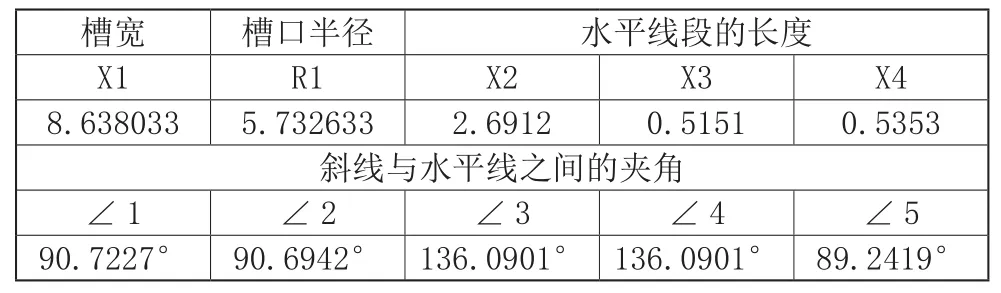
表3 工件2校正后参数值

参考问题三计算的参数估计值，我们对工件2校正后得到的参数估计值基本符合预计，只是由于9次局部测量可视化后的9条轮廓线重叠为3条，方便起见，我们仅计算了这3条可见轮廓线的各项参数，对其取均值作为工件2修正后的最终参数值，所以计算结果可能与真实值存在一定的差距。最后利用以上数据对最终的轮廓图进行修正，修正结果如图1.

图1 工件2修正轮廓图

3 结语

通过对接触式轮廓仪测量精度的研究，我们对产生测量误差的原因有了进一步的了解，并建立了偏移测量数据的校正模型，该模型对提高轮廓仪在实际生产中的测量精度具有重要作用，对新建道路路面平整问题具有推广意义。