信息量融入GA优化SVM模型下的地质灾害易发性评价

杨 康，薛喜成，李识博

(西安科技大学地质与环境学院，陕西 西安 710054)

进入21世纪以来，随着世界气候环境发生变化和人类活动能力及范围的不断扩大，地质灾害在自然因素和人类工程活动的双重驱动下呈现频发态势[1]。据自然资源部发布的《2020年全国地质灾害灾情及2021年地质灾害趋势预测》，2020年全国共发生地质灾害7 840起，共造成197人伤亡，直接经济损失达50.2亿元。为保障人们的生命财产安全、减少灾害损失、提高防灾减灾工作效率，开展地质灾害易发性评价和区划研究具有重要的应用价值[2]。然而地质灾害易发性评价结果的准确性所受到的制约因素较多且评价方法亦多种多样，如何选取适宜于研究区的评价方法，提高区域地质灾害易发性评价结果的准确性，成为国内外学者研究的一个重点和难点。

传统的地质灾害易发性评价方法如模糊逻辑法[3]、层次分析法[4]、证据权法[5]、确定性系数法[6]、信息量法[7]等在一定的地质环境背景下均能取得较好的综合分析效果。其中，信息量法因其原理简单、适用性强等特点，在区域地质灾害易发性评价中的运用最为广泛且评价效果相对较好。然而总的来看，基于模糊逻辑法、层次分析法等经验模型的地质灾害易发性评价方法在评价过程中具有较强的主观判断性，而基于证据权法、确定性系数法、信息量法等统计模型的地质灾害易发性评价方法又未能考虑各评价因子对地质灾害易发性的影响差异，这也是导致该类知识驱动方法评价结果精度值相对较低的主要原因。近年来，随着新智能算法的不断完善，各界学者开始将机器学习引入到地质灾害易发性评价研究中，该类基于数据驱动的分析方法通过对数据的训练[8]，能够较好地处理影响因子与地质灾害易发性之间的非线性关系，使得评价结果具有一定的可靠性。其中，支持向量机(SVM)是在结构风险最小化原理算法上的发展，其在一定程度上可以避免计算结果过拟合的现象[2]，相较于人工神经网络和随机森林模型具有数据量要求少、精度值更高等优点。尽管如此，在模型运算过程中，样本数据集的创建与模型各类参数值的设定均会在不同程度上对地质灾害易发性评价结果的准确性造成影响。

为合理设定支持向量机中的各类参数值，Zhou等[9]针对滑坡位移的步进特征，提出了基于诱发因素响应的粒子群优化与支持向量机耦合模型来预测滑坡位移；肖华瓶[10]在支持向量机算法的基础上，提出了蚁群支持向量机分类算法，其分类精度和收敛速度都有了较大的提升；唐跃等[11]基于交叉验证法对支持向量机模型进行了参数寻优，得到了最优爆破块度预测模型；Li等[12]基于滑坡监测数据，利用遗传算法优化支持向量机模型对滑坡位移率进行了预测。就优化算法而言，遗传算法具有强大的全局搜索能力，能在较短时间内搜索到全局最优点，且其适用范围较广，精度较高。为此，本文探索引入信息量法和遗传算法，提出一种信息量融入GA优化SVM模型下的地质灾害易发性评价方法，并将其运用于陕西省子长市地质灾害易发性区划分级研究中，以期能够为研究区内防灾减灾工作部署提供一定的理论参考。

1 研究区概况

陕西省子长市位于陕北黄土高原中部，介于东经109°11′58″～110°01′22″、北纬36°59′30″～37°30′00″之间，总面积为2 405 km2(见图1)。研究区地处华北陆块鄂尔多斯地块中东部，除在二叠纪末、三叠纪末、白垩纪末遭受区域隆升外，始终保持着稳定沉积盆地特征，无显著构造运动，褶皱构造总体表现为轴向近南北的大型宽缓向斜，次级褶皱以短轴背斜、鼻状背斜等平缓拱形隆起为主，断裂构造不发育[13]，总体地质构造较为简单。区内主要发育中-新生代地层，包括三叠系、侏罗系、白垩系、新近系和第四系，其中第四系黄土分布最为广泛，几乎遍布全区，其余时代地层多沿河谷两侧零星出露。

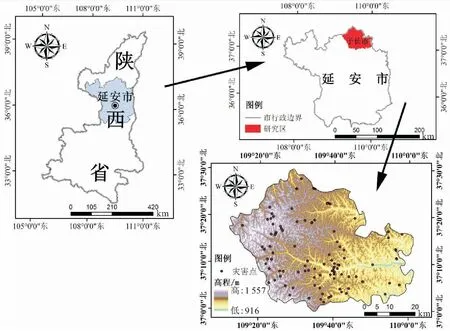
图1 陕西省子长市地理位置及地质灾害点分布图

研究区属温带半干旱大陆性季风气候，境内四季分明，总体气候特征为春季风大沙多，夏季炎热多雨，秋季凉爽多霜，冬季干旱寒冷[14]。年平均气温为9.1℃，极端最高气温为37.6℃，极端最低气温为-23.1℃，在黄土分布区易发生冻融，诱发地质灾害。境内河流属黄河水系，主要河流有秀延河、涧峪岔河、大理河和永坪河。各河流的相对比降大、峡谷多、曲度大、水流急，河水的主要来源为降水。受气候控制，多数冬、春二季枯水，进入夏、秋季节，洪水暴发，常泛滥成灾，由此诱发滑坡、崩塌、泥石流等地质灾害[15]。

2 地质灾害易发性评价方法

2.1 信息量模型

信息量(information value，简称INF)模型是一种源于信息量的统计预测方法，被学者们广泛运用于地质灾害易发性评价，其可以较好地反映各类成灾因子的相对敏感度和各类成灾因子中不同分级区间的贡献率的大小[16]。成灾因子的信息量值越大，对应区间内的地质灾害易发程度越高。信息量值由条件概率来计算，在实际运用中各成灾因子对地质灾害发生的贡献率用样本频率来计算，其数学表达式[7]为：

(1)

式中:IAi→B为成灾因子A中第i区间地质灾害发生的信息量值；Ni为成灾因子A中第i区间的地质灾害面积值或地质灾害点数量；Si为成灾因子A中第i区间的分布面积；S为研究区域总面积；N为研究区域内地质灾害总面积或地质灾害点总数量。

2.2 支持向量机模型

支持向量机(Support Vector Machines，简称SVM)模型是基于Vapnik-Chervonenkis理论和结构风险最小化原理的机器学习方法，该模型一般被用来解决线性不可分和非线性不可分的分类问题[17]。其基本思想是通过映射函数将低维空间非线性映射到高维空间中，求解最优线性分类面，从而使得所有样本与超平面距离最小。

假设n维空间训练样本集为{Xi，Yi}[i=1，2，…，n(n为样本个数)]，构造线性回归函数为

f(x)=ωφ(x)+b

(2)

式中：ω为方向向量;φ(x)为映射函数;b为偏置项。

求解ω和b的问题可转化为求目标函数的极值问题，其表达式为[18]

(3)

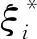
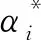
(4)

求解上述问题可得到SVM回归函数为

(5)

式中:K(xi,xj)=φ(xi)φ(xj)为内积核函数，SVM通过核函数将样本映射到更高维空间H，并在H中对原始问题进行线性分割。不同的核函数能构造输入空间不同类型的非线性决策面[19]，常见的满足Mercer条件的核函数包括线性核函数、多项式核函数、径向基核函数和sigmoid核函数，顾及到先验知识不足的情况，径向基核函数(Radial Basis Function,RBF)可以将样本映射到一个更高维空间，当类标签与特征之间的关系为非线性的样例时，可以得到较好的处理效果[20]，故本次选取RBF作为映射核函数。即：

K(xi,xj)=exp(-g‖xi-xj‖2)

(6)

式中:g为核函数参数，g>0。

2.3 遗传算法

遗传算法(Genetic Algorithm，GA)是在达尔文进化论和孟德尔遗传学理论的基础上发展起来的一种自适应启发式搜索算法，旨在模拟生物进化理论中最优生存的过程[21]。该算法具有较强的鲁棒性、并行性和全局寻优能力，在诸多领域得到了广泛的运用。遗传算法计算流程包括初始化种群、适应度值计算、选择、交叉和变异5个部分。首先，将问题的解编码为染色体，按照适应度函数的概率分布筛选出高适应度值的个体；再通过选择、交叉和变异3个基本的遗传算子使最具有生存能力的染色体以最大可能生存，群体逐代进化到搜索空间中越来越好的区域；最后，末代种群中的最优个体经过解码便可作为符合优化目标的近似最优解。

2.4 信息量融入GA优化SVM模型算法流程

在对信息量融入GA优化SVM模型进行训练之前需要构建样本数据集，样本数据集的准确性和合理性对模型的学习效果起着至关重要的作用。传统的样本数据集构建方法是通过对归一化后的各评价因子数据进行提取以创建样本数据集，但该类方法不能准确地对不同量纲评价因子赋值情况进行表征，而引入适应性较强的信息量模型则可以根据地质灾害点的空间分布特征以及评价因子不同分级的区间面积来进行求解，以得到更为合理的信息量值。提取各评价因子的信息量值来构建样本数据集不仅能够有效消除各评价因子在量纲和性质方面的差异，还可以有效地表示出各个评价因子的分级情况。在SVM模型进行学习的过程中，其关键参数c、g的设定亦会对评价结果造成显著的影响，其中，惩罚因子c决定了模型的训练误差和泛化能力，RBF核函数参数g影响样本在特征空间中的分布形式。GA与传统搜索算法的不同在于该算法并不是基于单一评估函数的梯度或较高次统计以产生一个确定性的实验解序列，而是通过模拟自然界的进化过程来搜索全局最优解[22]。本文通过将信息量与GA结合，构建信息量融入GA优化SVM的地质灾害易发性评价模型，解决了不同评价因子之间的量纲差异和SVM模型参数的赋值问题，提高了模型预测结果的精确度，最终达到提高地质灾害易发性评价结果准确性、合理性的目的。信息量融入GA优化SVM模型算法流程，见图2。

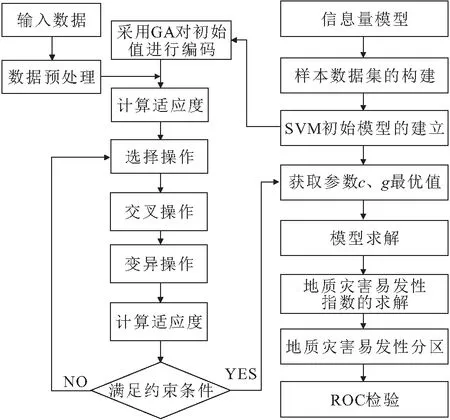
图2 信息量融入GA优化SVM模型算法流程图

具体的算法过程如下：

(1) 样本数据集的构建。首先根据地质灾害点的空间分布情况以及各评价因子分级情况，按照信息量模型求解得到各评价因子的信息量值；再选取同等数量的非地质灾害点，将信息量值提取至样本点上，共同构建样本数据集；然后以70%地质灾害点与相同数量的非地质灾害点的信息量值作为训练样本数据集，剩余的30%地质灾害点与相同数量的非地质灾害点的信息量值作为测试样本数据集。

(2) 信息量融入GA优化SVM模型。首先将构建的样本数据集导入MATLAB软件，采用GA对初始值进行编码，计算其适应度，然后通过选择、交叉和变异等操作直到满足约束条件以获取SVM中参数c、g的最优值。

(3) 地质灾害易发性指数的求解。在ArcGIS软件平台将全区转化为点，并将各评价因子信息量值提取至全区点集，代入训练好的模型中进行求解。由于模型输出的预测值是一个无标定量，为了使评价模型的输出结果能够作为地质灾害易发性指标LSI(Landslide Susceptibility Index)，需要将模型输出结果映射到[0,1]，其计算公式如下[23]：

(7)

式中：f(x)为SVM的输出值；A、B为待定系数，由贝叶斯公式和最大似然法估计确定。

(4) 地质灾害易发性分区。将模型求解得到的全区点集输出结果代入ArcGIS软件，按照地质灾害易发性指数将点转化为栅格，根据自然间断法与研究区实际情况将子长市地质灾害易发性划分为极低易发区、低易发区、中易发区、高易发区和极高易发区5个等级。

(5) 精度检验。为凸显信息量融入GA优化SVM模型的准确性与合理性，文中还建立了单一的信息量模型和信息量融入SVM模型对研究区地质灾害易发性进行评价，并对三类模型评价结果进行比较，最后采用受试者工作特征曲线对评价结果精度进行检验。

3 地质灾害易发性评价因子的选取与分级

子长市地质灾害类型发育有崩塌和滑坡两种，地质灾害的形成是多种成灾因子共同作用的结果，因此合理地选取适合于研究区的地质灾害易发性评价因子对地质灾害易发性评价结果至关重要。为保证评价结果的准确性与合理性，本文在野外调查工作的基础上，结合国内外较为普遍选用的评价因子，从地形地貌、地质环境和生态环境三个方面选取了高程、坡度、坡向、岩土体类型、地质灾害点密度、河流距离、道路距离、土地利用类型和年均降雨量9个地质灾害易发性评价因子。

3.1 地形地貌

地形地貌方面主要包括高程、坡度、坡向3个评价因子，地形地貌直接影响地质灾害的发生，其中坡度和高程直接影响地表松散堆积物的分布，并且随着坡度的增大，还会使得地表水径流明显变化[24]。研究区地形整体呈西高东低的趋势，综合考虑研究尺度以及区内地貌实际情况，将高程划分为916～1 100 m、1 100～1 200 m、1 200～1 300 m、1 300～1 400 m、1 400～1 557 m五个等级。子长市地质灾害点多分布在坡度为0～40°范围内，文中以10度间隔将坡度划分为0～10°、10～20°、20～30°、30～40°、>40°五个等级。坡向代表着山坡不同的日照程度，其不同程度地影响着地质灾害的易发性，本文基于ArcGIS坡向分析工具将坡向分为平面、北、东北、东、东南、南、西南、西、西北9种类型。

3.2 地质环境

地质环境方面包括岩土体类型、灾害点密度、河流距离和道路距离4个评价因子。研究区内岩土体类型可划分为软硬相间互层状含煤、油页岩碎屑岩类和软弱层状黏土岩类以及第四系黄土层3类，其中岩体多出露于深切河谷及强烈剥蚀后的山岭地带，区内第四系黄土体大面积出露，土体中的垂直节理和含水层段是其主要软弱结构面，滑坡、崩塌的发生常与其相关。综合考虑研究区地质灾害点数量以及分级效果，基于ArcGIS对灾害点进行密度分析，再将其以直线型阈值法进行归一化处理，最后按照相等间隔将灾害点密度划分为0.0～0.2、0.2～0.4、0.4～0.6、0.6～0.8、0.8～1.0五个等级，分别表示研究区内地质灾害点的分布情况。距河流的距离越近，对斜坡坡脚的冲刷、掏蚀作用愈明显，地质灾害易发性越高，在ArcGIS平台中以河流为中心做5个等级的缓冲区分别代表不同河流距离对地质灾害易发性的影响程度，河流距离划分为0～100 m、100～300 m、300～600 m、600～1 000 m、>1 000 m五个等级。道路的修建破坏了坡体原有的稳定结构，常常诱发各类地质灾害或存在较高的地质灾害隐患，距道路距离越近地质灾害易发性越高，本文以道路为中心向外以200 m为间隔做5个缓冲区将该道路距离划分为0～200 m、200～400 m、400～600 m、600～800 m、>800 m五个等级。

3.3 生态环境

生态环境方面包括土体利用类型和年均降雨量2个评价因子。其中土地利用类型一方面代表着不同强度的人类工程活动，另一方面也表征着不同区域的植被覆盖情况，本文将研究区土地利用类型划分为耕地、林地、草地、水体、建设用地和未利用地6种类别。降雨不仅能加快对坡面的冲刷侵蚀，还增加了岩土的孔隙水压力，从而诱发崩塌、滑坡灾害，子长市历年来地质灾害多发生于强降雨之后，本文选取子长市境内多个气象站站点2010—2015年的年平均降雨量进行空间插值得到降雨量分布图，并将其依照自然间断法将年均降雨量划分为489.09～514.15 mm、514.15～530.21 mm、530.21～546.28 mm、546.28～562.34 mm四个等级。

上述9个地质灾害易发性评价因子及其分级结果，见图3。

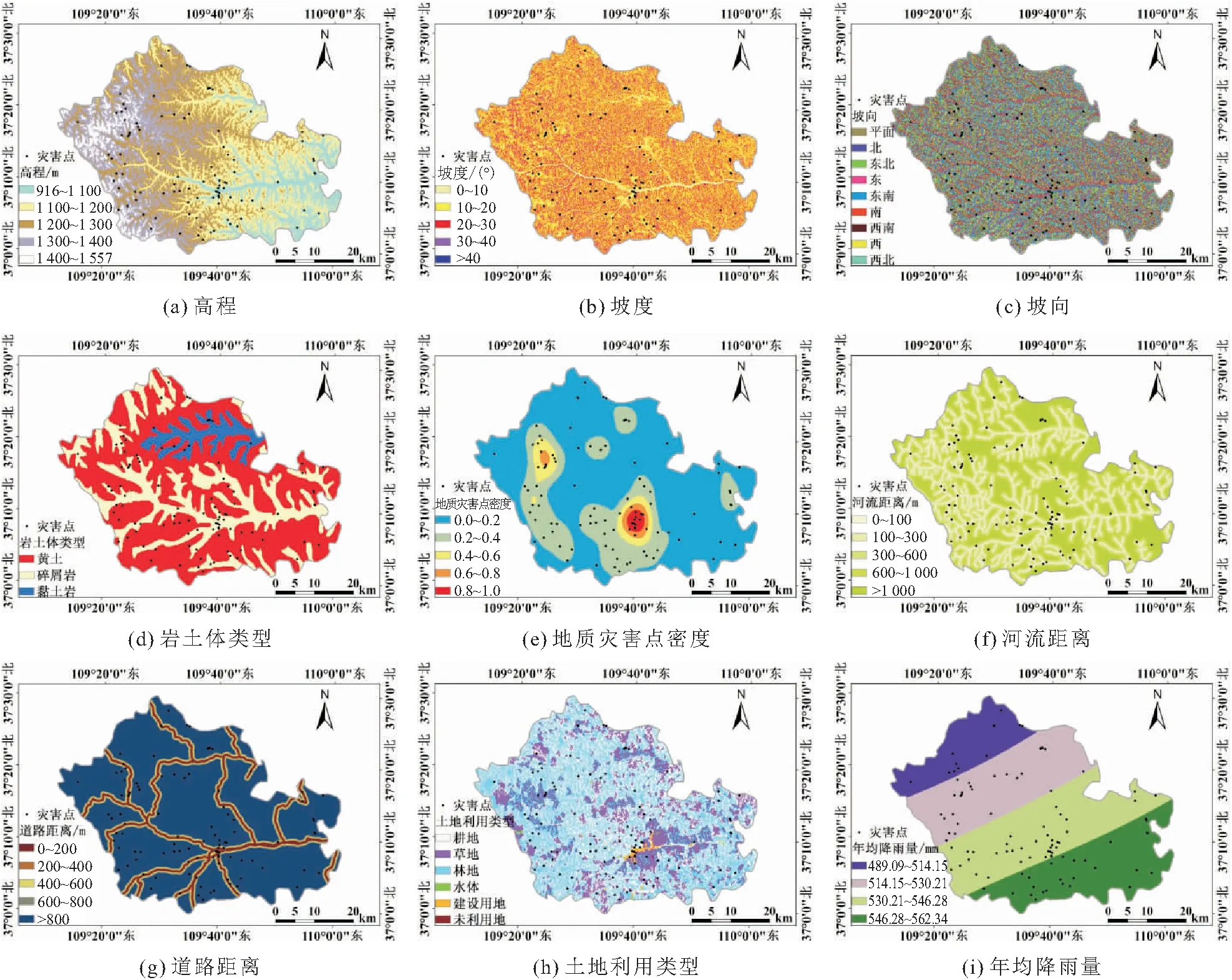
图3 地质灾害易发性评价因子及其分级

4 地质灾害易发性评价

4.1 评价因子信息量值的计算

各评价因子信息量值可以有效反映出对应评价因子对地质灾害易发程度的影响，同时单个评价因子不同分级下的信息量值也可对地质灾害易发程度进行定量描述。通过对9个评价因子不同分级下地质灾害点的空间分布情况进行统计，由公式(1)可计算得到各评价因子不同分级下的信息量值，结果见表1。

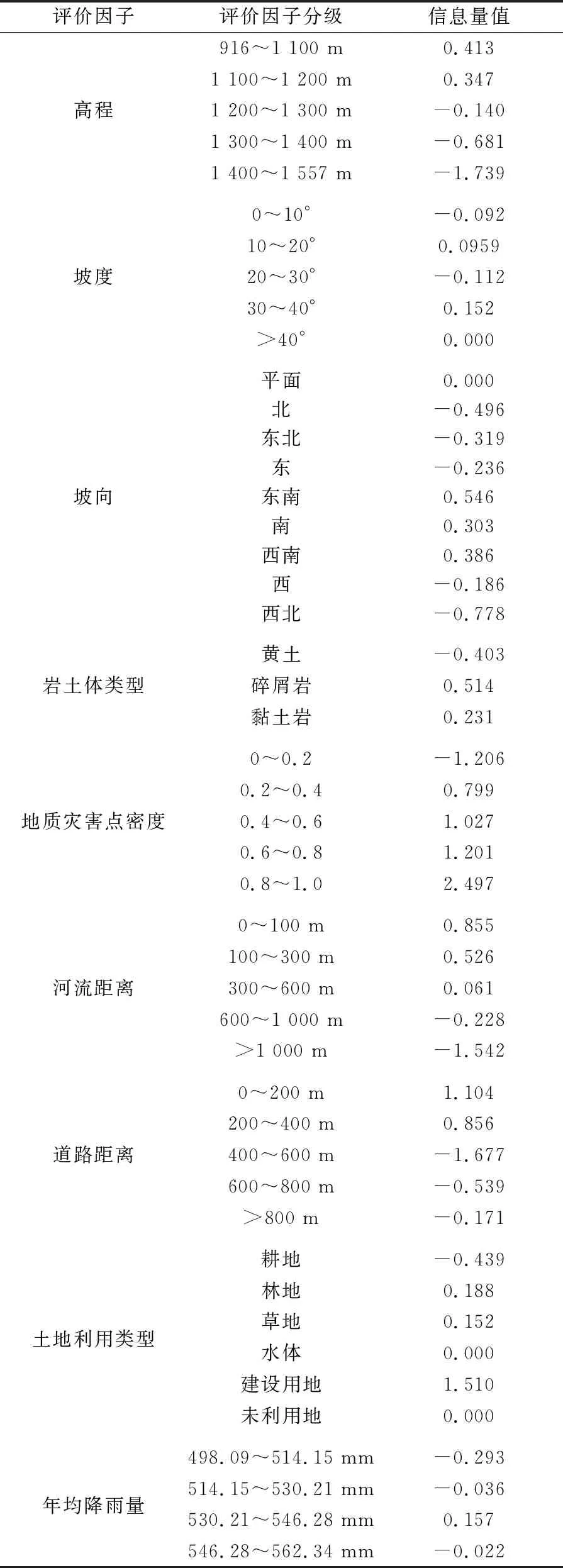
表1 各评价因子信息量值计算结果

4.2 信息量融入GA优化SVM模型

随机选取74处地质灾害点(约占地质灾害点数量的70%)与相同数量的非地质灾害点的信息量值组成训练样本数据集，剩余31处地质灾害点(约占地质灾害点数量的30%)与相同数量的非地质灾害点的信息量值组成测试样本数据集。

经过选择、交叉和变异等遗传操作得到SVM参数c、g的最优值分别为2.168、0.468。信息量融入GA优化SVM模型的参数适应度曲线，见图4。

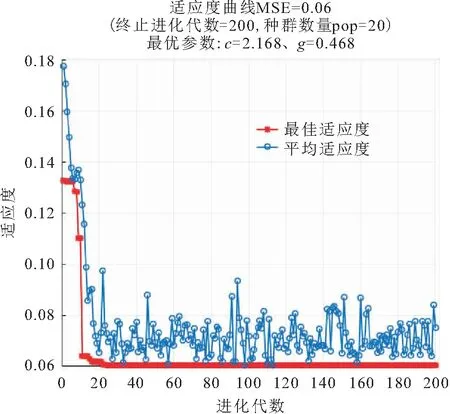
图4 信息量融入GA优化SVM模型的参数适应度曲线

由图4可知，在进化代数为30时，信息量融入GA优化SVM模型的参数最佳适应度曲线保持不变，适应度均方根误差约为0.06，表明在种群数量为200范围内已达到完全收敛。

将参数c、g值代入SVM模型中对训练样本进行学习，并利用测试样本数据对模型进行检验，得到信息量融入GA优化SVM模型的预测结果，见图5。

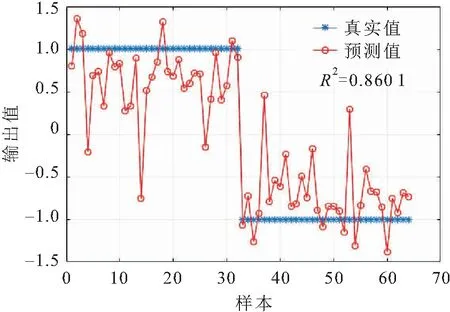
图5 信息量融入GA优化SVM模型的预测结果

由图5可知，信息量融入GA优化SVM模型的预测效果较好，回归系数R2达到0.8601，表明该模型的预测精度较高。

4.3 评价结果与分析

将全区转化为点集，并将各点对应的9个评价因子的信息量值进行提取并导入训练好的模型中，利用公式(7)对模型输出值进行处理得到各点对应的地质灾害易发性指数值，将其导入ArcGIS软件，以信息量融入SVM易发性指数值作为分类依据，按照自然间断法对研究区地质灾害易发性进行重分类，得到子长市地质灾害易发性评价区划图，见图6(a)。为凸显出信息量融入GA优化SVM模型的评价结果的合理性和适用性，本文对信息量(INF)模型和信息量融入SVM(INF-SVM)模型进行求解，得到这2种模型下的子长市地质灾害易发性评价区划图,见图6(b)和(c)。分别对3种评价模型下的子长市地质灾害易发性评价分区情况与地质灾害点分布数量进行统计，结果见表2。

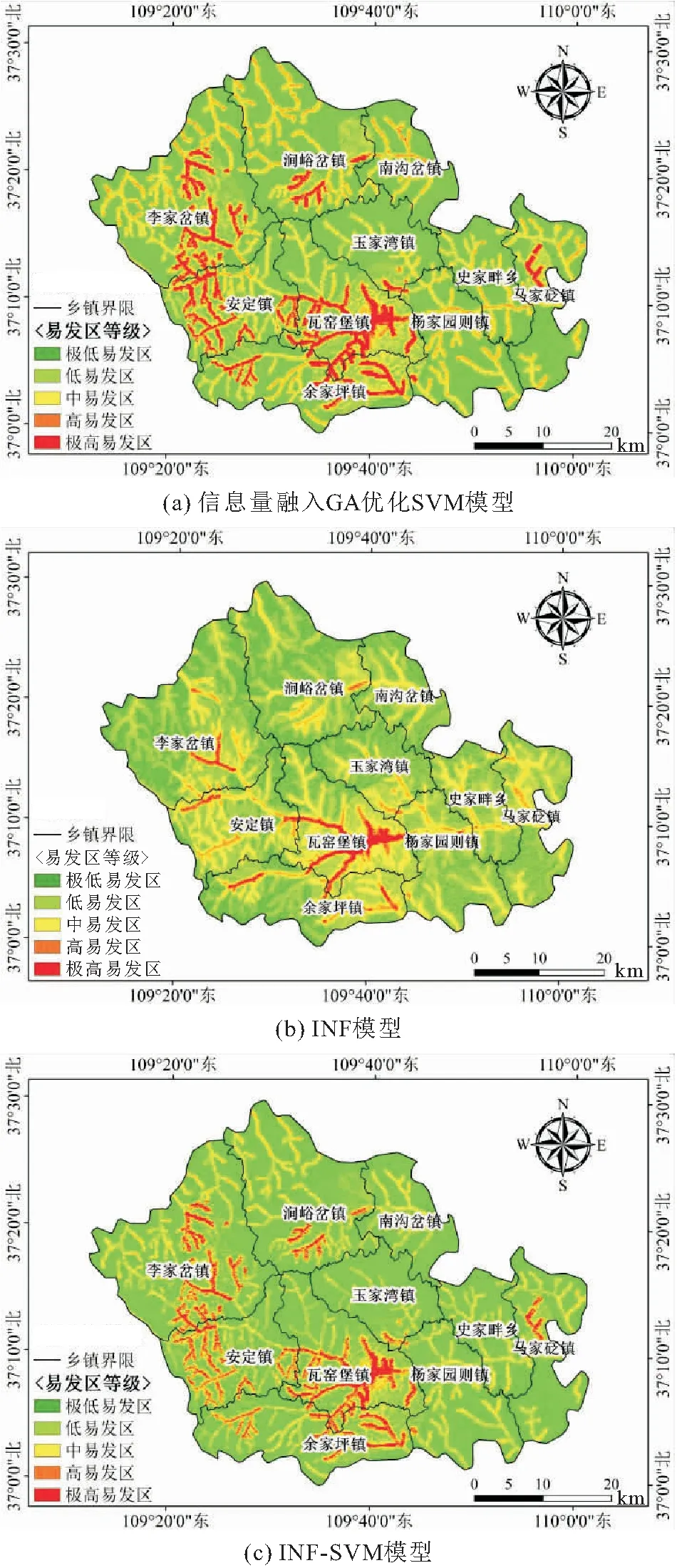
图6 3种评价模型下子长市地质灾害易发性评价区划图

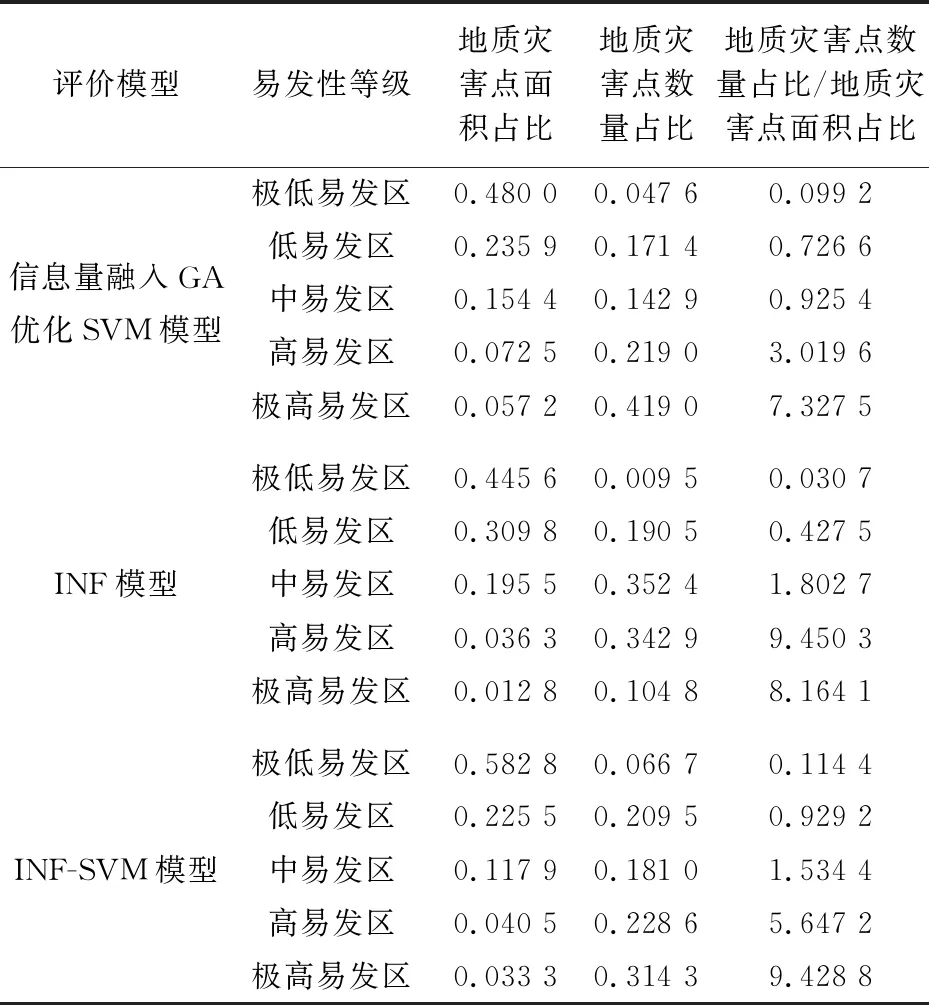
表2 3种评价模型下子长市地质灾害易发性分区统计结果

由图6可知，3种评价模型下求解得到的研究区地质灾害易发性区划图基本一致。其中，传统信息量模型直接对各类评价因子的信息量值进行叠加处理，评价结果的区划效果较为明显，区内中研究区易发区分布较广；而支持向量机模型本质上是对地质灾害点和非地质灾害点的各评价因子特征进行学习，综合考虑各评价因子与地质灾害易发性的非线性关系，并基于此进行全区地质灾害易发性预测，由于研究区内人类工程活动较为强烈，区域内地质灾害点数量也随之分布较多，故评价结果表现为极高、高易发区集中于研究区中部、并沿道路和河流呈现树枝状分布。

由表2可知，3种评价模型下求解得到的子长市地质灾害点面积占比均表现为由极低易发区向极高易发区逐级递减、地质灾害点密度(地质灾害点数量占比/地质灾害点面积占比)由极低易发区向极高易发区基本保持逐级递增趋势，表明3种模型的评价结果均较为合理，其中基于信息量融入GA优化SVM模型的子长市地质灾害易发性分区评价结果在极高易发区中地质灾害点数量占比高于INF模型和INF-SVM模型，说明本文所建立的信息量融入GA优化SVM模型对子长市地质灾害易发性分区更为合理，评价结果适用性更强。

现对信息量融入GA优化SVM模型下的子长市地质灾害易发性评价结果概述如下：

(1) 地质灾害极高、高易发区主要分布于研究区中南部、西部地区，面积约为312 km2，占全区总面积的12.97%，区内地质灾害点数量占全区地质灾害点总数的63.80%。对比本次子长市地质灾害调查结果可知，该两类分区内的人口密度相对较大，加之修建道路、铁路等，使得该区域内地质灾害发育较多，居民承灾体易损性高，属于地质灾害防灾减灾的重点研究区域。

(2) 地质灾害中易发区呈树杈状沿河流、道路分布，面积为371 km2，占全区总面积的15.44%，区内地质灾害点数量占全区地质灾害点总数的14.29%。受到河流对斜坡冲刷作用及人工切坡建房等因素的影响，该分区内地质灾害通常表现为规模较大，居民承灾体易损性相对较高。

(3) 地质灾害低、极低易发区在全区分布最广，两类分区下的面积约为1 722 km2，占全区总面积的71.59%，区内地质灾害点数量占全区地质灾害点总数的21.90%。受土地利用类型、坡度、高程等因素的综合影响，此两类分区内的地质灾害通常表现为规模较小，强度较低，影响范围较小且易损性较低。

4.4 评价结果检验

受试者工作特征(Receiver Operating Characteristic，ROC)曲线是根据一系列不同的二分类方式做出的曲线，用于反映所用分析方法的特异性与敏感性之间的相互关系，曲线下面积(Area Under Curve，AUC)可以表示模型对地质灾害样本的预测精度，AUC取值范围为[0.5,1]，其值越大表明预测精度越高。本文选取研究区内105个地质灾害点和同等数量的非地质灾害点对3种模型下的子长市地质灾害易发性评价结果进行精度检验。3种评价模型的ROC曲线，见图7。

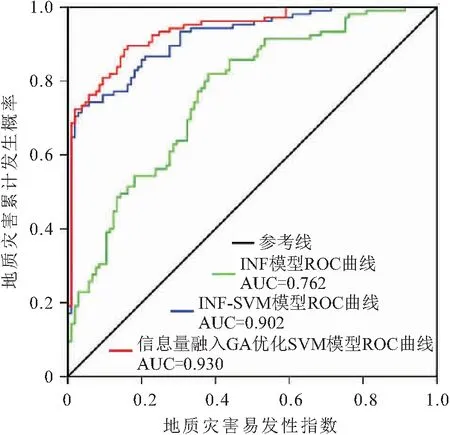
图7 3种评价模型的ROC曲线

由图7可知，信息量融入GA优化SVM模型ROC曲线的AUC值最高，为0.930，其次为INF-SVM模型，INF模型最小，表明采用信息量融入GA优化SVM模型能够客观、准确地对子长市地质灾害易发性进行分级评价，且评价结果的精度在3种评价模型中最高。

5 结 论

本文以子长市作为研究区，从地形地貌、地质环境、生态环境三个方面选取了高程、坡度、坡向、岩土体类型、地质灾害点密度、河流距离、道路距离、土地利用类型和年均降雨量作为地质灾害易发性评价因子，将传统的信息量模型与SVM相结合，利用GA对SVM关键参数进行优化选取，建立了信息量融入GA优化SVM地质灾害易发性评价模型，并将其运用于研究区地质灾害易发性评价，同时与单一的信息量(INF)模型和信息量融入SVM(INF-SVM)模型的评价结果进行了比较，得到如下结论：

(1) 利用GA对SVM进行优化处理，得到SVM参数c、g的最优值分别为2.168、0.468、信息量融入GA优化SVM模型的适应度曲线均方根误差为0.06，且在测试集样本中回归系数R2为0.860 1，表明GA优化效果较好，信息量融入GA优化SVM模型可以有效减少SVM关键参数值的设定对评价结果造成的影响。

(2) 研究区地质灾害极高、高易发区主要分布于研究区中南部、西部，区域内地质灾害受到人类工程活动的影响较大，地质灾害的发生常具有较高的易损性，为地质灾害防灾减灾工作的重点规划区域；地质灾害中易发区主要沿部分道路及支流呈树枝状散布，区内地质灾害的发生受到自然因素影响的较多，地质灾害点数量占比相对较少；地质灾害低、极低易发区在整个研究区范围内分布最广，区域内人口相对较少，人类工程活动强度较低，地质灾害的发生也相对较少。

(3) INF模型、INF-SVM模型和信息量融入GA优化SVM模型3种评价模型下得到的子长市地质灾害易发性分区评价结果基本保持一致，经ROC曲线检验，基于信息量融入GA优化SVM模型的ROC曲线AUC值为0.930，其评价结果的精度最高，表明该评价模型的评价效果较好。

(4) 将传统的评价模型与机器学习模型相结合能够有效避免单一评价模型的局限性，同时利用优化算法对模型进行优化处理能够有效解决模型参数的赋值问题。本文提出的信息量融入GA优化SVM模型在地质灾害易发性评价中的研究结果经检验具有一定的可靠性，可为学者在同等地质环境条件下的地质灾害评价工作提供一定的参考，同时也为子长市区域地质灾害风险管控措施的制定提供了一定的理论基础。