四旋翼无人机滑模变结构控制

许靖 靳宇星 杨永春

摘要：针对四旋翼无人机飞控系统中传统的PID控制算法响应速度慢、控制精度低以及鲁棒性不够强的问题，通过采用滑模变结构的控制算法取代了传统的PID控制算法，增强了系统的控制精度和响应速度。由于无人机在飞行过程中容易受到各种外界环境因素的干扰，因此采用积分滑模的控制策略来提升飞控的抗干扰能力。同时考虑到四旋翼无人机固有的欠驱动性，将无人机控制系统分为位置子系统外环和姿态子系统内环的结构，通过内外环的控制策略可以简化欠驱动系统控制律的设计过程。

关键词：四旋翼无人机;飞控系统;内外环控制;滑模控制

中图分类号：TP273      文献标识码：A

文章编号：1009-3044（2022）10-0116-03

1 引言

四旋翼无人机具有结构紧凑、操作简单、成本低、能够实现垂直起降，定点悬停等功能，且对起降地形环境要求低等优点，广泛地应用在航拍、农林植保、电力巡线、测绘以及军事侦察等各行各业中[1]。

四旋翼无人机的飞行是通过安装在机臂上的四个电机带动螺旋桨的旋转，从而实现在空间位置上的上、下以及前、后、左、右等六个自由度方向的移动。因此，四旋翼无人机系统是一个典型的欠驱动控制系统，其选用的控制策略和飞控中的控制方法是无人机飞行控制的核心。但其本身具有的非线性及欠驱动性给控制器的设计带来了巨大的困难，同时无人机在飞行过程中易受到外界环境的干扰，如气流、温度、沙尘等因素，因此控制策略需要具备一定的抗干扰能力。

目前，传统的四旋翼无人机的控制策略主要是采用PID控制[2]。PID是控制领域中一种较为简单也是比较成熟的控制方式，经过百年时间的应用和发展，已经在工业生产的各个领域有广泛的应用。其在四旋翼无人机的应用上也较为成熟。但传统的线性控制如PID控制[3]、H_∞控制[4]、LQR控制[5]等策略在处理非线性问题和控制欠驱动系统时具有设计结构复杂、动态响应不足和抗干扰能力弱的缺点。因此，需要寻求一种非线性控制策略来应对欠驱动系统。其中滑模变结构控制具有响应快速，抗干扰能力强，对系统参数依赖性小的优点，用来设计四旋翼无人机的欠驱动控制能够提高其控制性能。

2 四旋翼无人机的建模

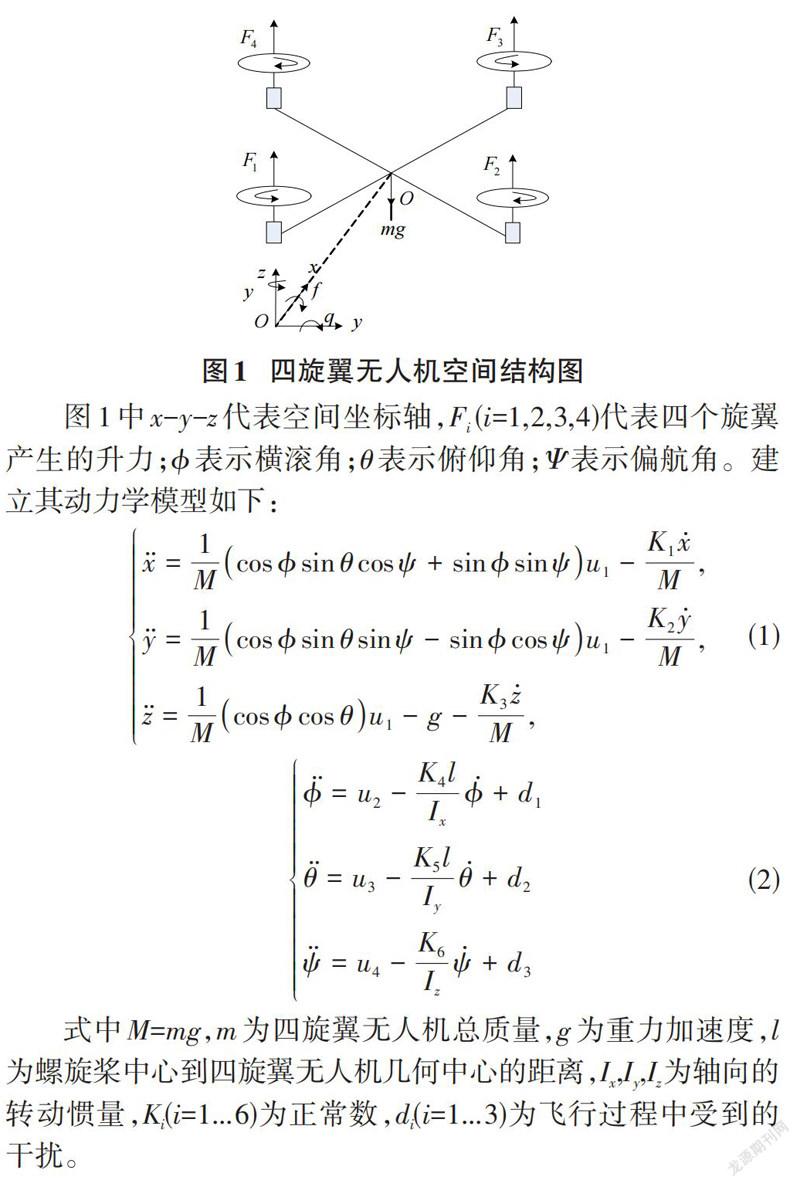
四旋翼无人机的结构是由交叉组成的四个机臂和电机构成的，常见的主要有“+”结构和“×”结构两种[6]。本文选取“×”结构进行分析研究，其在空间坐标轴下的结构如图1所示。

图1中x-y-z代表空间坐标轴，Fi （i=1，2，3，4）代表四个旋翼产生的升力;ϕ表示横滚角;θ表示俯仰角;Ψ表示偏航角。建立其动力学模型如下：

[x=1Mcosϕsinθcosψ+sinϕsinψu1-K1xM， y=1Mcosϕsinθsinψ-sinϕcosψu1-K2yM，z=1Mcosϕcosθu1-g-K3zM，]     （1）

[ϕ=u2-K4lIxϕ+d1 θ=u3-K5lIyθ+d2ψ=u4-K6Izψ+d3]           （2）

式中M=mg，m为四旋翼无人机总质量，g为重力加速度，l为螺旋桨中心到四旋翼无人机几何中心的距离，Ix，Iy，Iz为轴向的转动惯量，Ki（i=1...6）为正常数，di（i=1...3）为飞行过程中受到的干扰。

针对四旋翼无人机的欠驱动特性，为避免欠驱动控制律直接设计的复杂性，采用了内外环结构设计控制律。将四旋翼无人机控制系统分为了位置子系统外环和姿态子系统内环的内外环结构来分别设计控制了，这种方法可以使得控制器的设计更为简单可靠。系统的设计结构图如图2所示。

3 四旋翼无人机控制律设计

3.1 位置控制律设计

由无人机数学建模式（1）可以看出其在x-y-z空间位置方向有三个自由度，但却只有一个独立的控制变量，因此需要进行解耦控制。分别沿x-y-z轴方向构造如下函数：

[u1x=1Mcosϕsinθcosψ+sinϕsinψu1u1y=1Mcosϕsinθsinψ-sinϕcosψu1u1z=1Mcosϕcosθu1]       （3）

将式（3）带入无人机动态模型式（1）可得：

[x=u1x-K1xM， y=u1y-K2yM，z=u1z-g-K3zM，]         （4）

针对式（4）为使系统的跟踪误差能够快速准确地收敛到零，采用滑模控制律来设计该控制系统，并取x-y-z轴方向的三个误差函数如下：[ex=xd-x]，[ey=yd-y]，[ez=zd-z]。同时，为提高系统的控制精度采用积分滑模分别设计三个滑模函数为[sx=ex+C10texτdτ]，[sy=ey+C20teyτdτ]，[sz=ez+C30tezτdτ]，則对以上三个滑模函数求其一阶导数并将式（4） 带入可得：

[sx=ex+C1ex=xd-u1x-K1xM+C1exsy=ey+C2ey=yd-u1y-K2yM+C2eysz=ez+C3ez=zd-u1z-g-K3zM+C3ez]     （5）

根据我国学者高为炳院士提出的滑模控制趋近律的概念，基于趋近律法的滑模变结构控制能够有效地抑制滑模控制中的抖振问题提高误差的收敛速度，因此选取指数趋近律[s=-ks-ηsgns]，同时为进一步减小滑模控制中的抖振，用饱和函数代替控制律的开关函数，由此可设计控制律为：

[u1x=xd+K1xM+C1ex+k1sx+η1satsxu1y=yd+K2yM+C2ey+k2sy+η2satsyu1z=zd+K3zM+C3ez+k3sz+η3satsz]       （6）

根据李亚普洛夫方程可以验证所设计的控制系统是稳定的。

根据四旋翼无人机的飞行指令的要求，通常情况下会给定位置指令和航向指令，因此位置控制环需要根据给定的位置和航向指令生成姿态角，因此假定满足控制律式（6） 所需的无人机姿态角度为θd和ϕd，则由式（3） 可以求决出姿态环所需的给定信号，过程如下：

[u1x=u1ztanθdcosψd+u1ztanϕdsinψdcosθdu1y=u1ztanθdsinψd-u1ztanϕdcosψdcosθd]          （7）

进一步对式（7） 进行求解θd和ϕd的运算，则可以得到：

[θd=arctancosψdu1x+sinψdu1yu1z]             （8）

[ϕd=arctancosθdsinψdu1x-cosψdu1yu1z]           （9）

由此，姿态控制内环所需的给定信号θd和ϕd已经确定，据此位置控制律u1可设计为：

[u1=Mu1zcosψdcosθd]           （10）

3.2 姿态控制律设计

姿态控制律同样采用积滑模控制来设计，设计思路和设计过程同位置控制律的设计。定义三个姿态角的误差函数为：[eϕ=ϕd-ϕ]，[eθ=θd-θ]，[eψ=ψd-ψ]。同样选取积分滑模面如下：[sϕ=eϕ+C40teϕτdτ]，[sθ=eθ+C50teθτdτ]，[sψ=eψ+C60teψτdτ]，

则同位置控制律的设计可得姿态控制律如下：

[u2=ϕd+K4lIx+C4eϕ+k4sϕ+η4satsϕu3=θd+K5lIy+C5eθ+k5sθ+η5satsθu4=ψd+K6lIz+C6eψ+k6sψ+η6satsψ]     （11）

同样可根据李亚普洛夫方程验证姿态控制系统是稳定的，姿态误差呈指数形式快速收敛为零。

4 MATLAB仿真实验

本文利用MATLAB仿真软件，搭建四旋翼无人机的数学模型和所设计的控制系统。运行过程中给定相关的仿真参数如下：

四旋翼无人机机体参数给定如下：m=2，l=0.2，g=9.8;K1=K2=K3=0.01;K4=K5=K6=0.012;Ix=Iy=Iz=1.25;d1=d2=d3=0.2。

取控制器参数C1= C2= C3=0.2;C4= C5= C6=0.8;k1= k2=k3=4;k4= k5=k6=20;ηi（i=1，2，3，4，5，6）=2。移动机器人初始位置位于[2，1，0]，取zd=3，θd=60°。

仿真实验是通过位置控制器和姿态控制器，使得四旋翼无人机能过够快速准确地跟踪到给参考点位，仿真结果如下：

图3给出了四旋翼无人机在仿真软件中的位置方向的轨迹跟踪曲线。由图可以看出，在仿真开始后四旋翼无人机能够快速的响应并1秒钟之内跟踪到给定的参考位置，说明所设计的系统能够满足控制要求。

图4给出了四旋翼无人机在仿真软件中的姿态跟踪曲线。红色为给定角度和根据给定目标计算出来的参考曲线，黑色为实际运行曲线。由图可以看出所设计的控制器能够快速准确地跟踪上两个位置方向和一个角度方向的移动轨迹，确保系统的稳定运行。

5 结束语

针对四旋翼无人机控制系统，采用内外环双闭环的控制结构，用控制性能更好的滑模变结构控制策略，取代传统的PID控制策略。该设计方法既减小了控制器的设计难度，又提高了系统的响应能力和控制精度，同时滑模控制本省还具有很强的鲁棒性，可以增强四旋翼无人机的抗干扰能力。最后在MTLAB仿真软件中验证了设计的正确性。

参考文献：

[1] 张磊.基于滑模变结构控制的四旋翼无人机应用分析与研究[J].工业控制计算机，2021，34（12）：73-75.

[2] 胡徐胜，郑睿，陶彬彬.四旋翼无人机飞控系统设计与实现[J].廊坊师范学院学报（自然科学版），2021，21（4）：46-50.

[3] 邵霖文，廖芳，丁黎明，等.基于MATLAB的四旋翼无人机飞控PID仿真设计[J].山西电子技术，2021（5）：43-46.

[4] 丁力，李兴成，冯俊萍，等.四旋翼飞行器静态H∞输出反馈控制[J].电光与控制，2018，25（4）：41-45.

[5] 鲜斌，张旭，杨森.无人机吊挂飞行的非线性控制方法设计[J].控制理论与应用，2016，33（3）：273-279.

[6] 向朝兴，茅健.四旋翼无人机的旋翼空气动力学建模与仿真[J].计算机仿真，2021，38（10）：48-52.

【通联编辑：谢媛媛】

收稿日期：2022-01-25

基金项目：新疆交通职业技术学院科研课题（项目编号：J-21-08）

作者简介：许靖（1991—） ，女，新疆乌鲁木齐人，硕士，研究方向为智能控制;靳宇星（1990—） ，男，甘肃天水人，讲师，硕士，研究方向为控制理论、无人机控制;杨永春（1972—） ，女，新疆乌鲁木齐人，教授，研究方向为電气自动化。