油气悬架车身高度控制研究

柯欢欢++管继富++黄刚

摘 要：针对油气悬架系统，提出了一种由PID控制器和滑模控制器组成的双闭环控制的车身高度控制策略，外环为高度控制环，内环为力跟踪控制环。外环利用PID控制算法实现对期望高度的精确跟踪，输出一个最优控制力，该最优控制力作为内环的给定。内环的作用是通过油气悬架实现对最优控制力的跟踪，针对建立的油气悬架非线性数学模型，内环采用滑模控制算法，并对滑模控制存在的颤振问题进行了修正。结果表明，该控制器能满足车身高度控制的精度要求，同时具有较好的快速性和稳定性。

关键词：高度控制；油气悬架；非线性控制；滑模控制

中图分类号：TP13 文献标识码：A

The Study of Vehicle Height Control Based on Hydropneumatic Suspension

Ke Huanhuan，Guan Jifu，Huang Gang

（School of Mechanical and Vehicular Engineering， Beijing Institute of Technology， Beijing 100081， China）

Abstract：A control strategy of vehicle height was proposed for the hydropneumatic suspension system， which was a double closed-loop control system composed by PID controller and sliding mode controller（SMC）that the outer loop was the height control loop and the inner loop was the force tracking control loop. The outer loop utilized the PID control as height controller which could output an optimal control force that served as the input of the inner loop to track the desired height. The function of the inner loop was to realize the tracking of the optimal force through the hydropneumatic suspension. The SMC was adopted by the inner loop and the problems of chattering existed in the SMC were corrected for the established nonlinear mathematical model. The results indicate that the control strategy proposed in this paper could satisfy the accuracy requirement of vehicle height control with excellent rapidity and stability.

Key words：height control；hydropneumatic suspension；nonlinear control；sliding mode control

油气悬架系统可以实现充放油控制，只要附加必要的阀组、管路、油泵及油箱等部件，通过所设计的控制器可以实现车辆的高度控制[1-2]。对于以车体高度控制为基础的整车调平系统，能够为军用装甲车辆的火控射击提供一个相对稳定的车体平台。

传统油气悬架的车身高度控制，都是基于一定规则的if-then，if-else软件编程调平。工程实践证明，此种方法在调平到达期望高度时，有明显的振荡。这是由于调节时的液压阀开口面积为定值，只有到达所规定的高度时才完全闭锁；在车体惯性作用下产生振荡，设置不当还会使误差增大。所以需要设计基于模型的控制器。

Akar等人[3]建立了油气悬架的非线性动力学模型，外环通过期望车身高度与实际高度的偏差，利用PID控制算法求出期望力，内环利用滑模控制算法对期望力进行跟踪，通过不断反馈修正控制车身高度。但在研究过程中没有考虑轮胎刚度及减振器对悬架系统的影响。陈志林[4]通过变结构与PID联合控制求出期望车身高度所需要的流量，所设计的控制器可使车身高度较快达到期望值，减弱了摩擦力带来的系统振荡问题。但是，悬架在目标高度存在抖动。空气悬架领域，Kim等人[5]利用三阶滑模控制算法，针对空气悬架系统进行了整车的高度控制研究。

研究考虑执行元件动力学特性的整车悬架系统车身高度控制技术在汽车悬架研究中具有重要意义。到目前为止，多数悬架车身高度控制，在研究过程中假设力执行元件具有理想特性[6]。但由于执行元件动力学较为复杂，油液压缩和伺服阀流量的非线性，都将引起车身位移的振荡，使控制车身高度更加困难。只有少数深入分析了执行元件与悬架系统的相互作用关系[7]，而且在建模过程中没有考虑减振器和轮胎刚度[8]。

本文基于某轮式特种车辆油气悬架的实物模型，在考虑减振器、轮胎刚度的情况下，建立非线性数学模型，在车辆静止状态下进行油气悬架车身高度控制的研究。为克服油气悬架系统中的非线性和不确定性，采用滑模控制算法提高控制精度。

1 非线性油气悬架模型

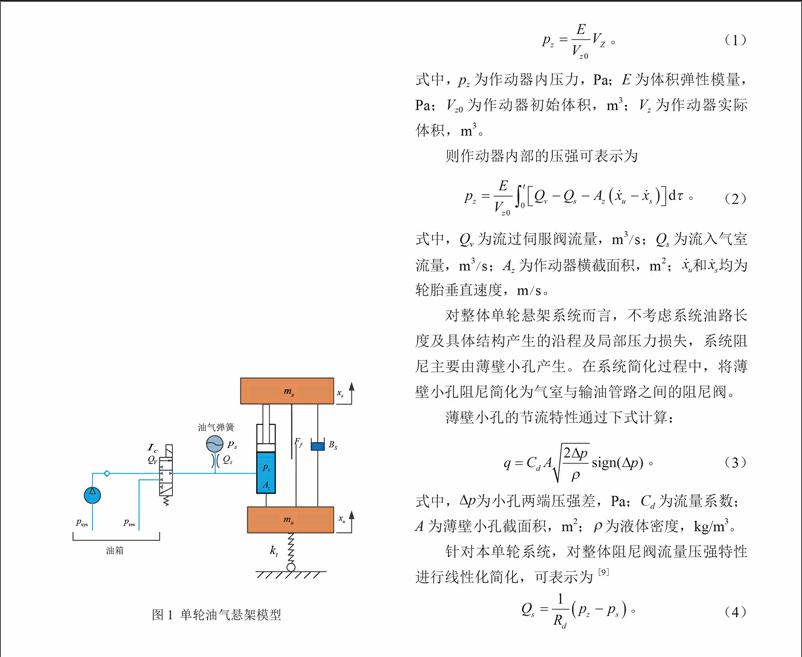
本部分针对单轮油气悬架进行非线性化建模，如图1所示。单轮油气悬架是二自由度的系统，由控制阀组、油气弹簧、油源系统组成。

图1 单轮油气悬架模型

作用在流体上的压力变化可引起流体体积和密度的变化，这一现象称为流体的可压缩性。一般用体积弹性模量 来表示。作动器内体积与压强之间有如下关系[8]：

。 （1）

式中， 为作动器内压力， ； 为体积弹性模量， ； 为作动器初始体积， ； 为作动器实际体积， 。

则作动器内部的压强可表示为

。 （2）

式中， 为流过伺服阀流量， ； 为流入气室流量， ； 为作动器横截面积， ； 为轮胎垂直速度， ； 为轮胎垂直速度， 。

对整体单轮悬架系统而言，不考虑系统油路长度及具体结构产生的沿程及局部压力损失，系统阻尼主要由薄壁小孔产生。在系统简化过程中，将薄壁小孔阻尼简化为气室与输油管路之间的阻尼阀。

薄壁小孔的节流特性通过下式计算：

。 （3）

式中， 为小孔两端压强差， ； 为流量系数；A为薄壁小孔截面积， ；ρ为液体密度， kg/m3。

针对本单轮系统，对整体阻尼阀流量压强特性进行线性化简化，可表示为[9]

。 （4）

式中， 为阻尼阀等效阻尼系数。

考虑气室中的工作气体为氮气，其气体特性按照理想气体状态方程计算，表达为

。 （5）

式中， 为气体多变指数； 为气室中的初始压力， ； ； 为气室中的初始体积， 。

由于气室内气体体积的变化等于流入气室的流量 的相反数，所以：

。 （6）

本系统通过伺服阀来控制油液流入或流出作动器。如果控制输入电流为正，伺服阀接通高压源，将油液压入作动器。如果控制输入电流为负，接通低压源，油液流回油箱。油液流经伺服阀，可以精确地建立如下模型[3]：

。 （7）

式中， 为系统的压力， ，需大于作动缸的压力； 为油缸的压力，接近于100 kPa。

建立油气悬架单轮动力学模型：

。 （8）

作动器内的摩擦力可以对压力产生显著的影响，所以不可以被忽略。本文所采用的摩擦力模型为[10]

。 （9）

式中， 。摩擦力与速度之间的关系如图2所示。

摩擦力Ff/N

速度v/（m·s-1）

图2 摩擦力与速度的关系

依据上述各式，建立单轮系统的非线性状态空间方程。

定义状态变量为 。

控制输入为： 。

因此，本系统的状态空间模型可表示为

。 （10）

式中， ； ； 。

2 控制系统结构

本文所采用的控制系统结构由两个子控制器组成，如图2所示， 为期望的车身高度。控制系统内环控制使用滑模控制算法，外环控制采用积分分离PID控制算法。积分分离PID控制律通过期望车身升起的高度和通过单轮悬架反馈的车身高度，求出期望的控制力输入控制内环，控制内环通过将期望控制力和作动器产生力产生的差值进行滑模控制，求出伺服阀所需电流并输入到单轮悬架系统，所产生的车身高度再次与期望的车身高度进行比较，并输入外环车身控制器。通过反馈不断修正，使车身达到理想的高度。

2.1 积分分离PID控制

本文设计的外环控制器，采用积分分离PID控制算法。积分分离控制的基本思路是，当被控量与设定值偏差较大时，取消积分作用，以免由于积分作用使系统稳定性降低，超调量增大；当被控量接近给定值时，引入积分控制，以便消除静差，提高控制精度[11]。外环需使车身的实际位移跟踪给定的期望位移，并计算出期望的力 。

给定参考信号 ，定义 为跟踪误差。根据仿真情况，设定 。

当 时，采用PD控制，控制律为

。 （11）

当 时，采用PID控制，控制律为

。 （12）

根据对系统内环特性的分析，选定合适的控制器参数。

2.2 滑模控制

由于油液的可压缩性，使油气悬架具有高度的非线性。为了确保作动器的压力精确地跟踪期望的压力，需要克服其非线性和不确定性。由于滑模控制能有效地抑制非线性和不确定性，所以本文的内环控制器采用滑模控制算法。

滑模运动包括趋紧运动和滑模运动两个过程。系统从初始状态趋向切换面，直到到达切换面的运动称为趋紧运动，即趋近运动为 的过程。根据滑模变结构原理，滑模可达性条件仅保证由状态空间任意位置运动点在有限时间内到达切换面的要求，而对于趋近运动的具体轨迹未作任何限制，采用趋近律的方法可以改善趋近运动的动态品质[12]。

图3 控制器结构

滑动曲面被定义为：

。 （13）

式中， 为系统的相对阶数； 为正常数； 为期望的压力， 。

滑模控制律可由非线性的单轮动力学模型（8）和所定义的滑动曲面（13）求得。作动器的非线性模型为

。 （14）

式中， 为伺服阀所需电流， 。

。 （15）

由于 、 的参数和动态特性不精确知道，假定 的估计误差受已知函数的限制，即

。（16）

式中， 和 为不确定模型 和 的估计值； 。控制增益 界已知，即

。 （17）

由于控制输入以乘积的形式出现在动态模型中，所以将上述界的平均值作为 的估计 ，即

。 （18）

式（10）是一阶非线性系统，所以滑动曲面的相对阶数 ，由式（12）得到：

。 （19）

于是有：

。 （20）

使 的一个连续控制律为

。 （21）

由于所设计的控制律，需要系统轨线一直停留在滑动曲面上。所以系统轨线需满足如下滑动条件：

。 （22）

式中， 为正常数。本文为改善趋近运动的动态品质，采用指数趋近律。即

。 （23）

式中， 为不确定边界所定义的常数，满足：

（24）

所以单轮悬架控制系统的控制律为：

（25）

为观察跟踪效果，假设以某期望压力值 输入，采用此趋近律，滑模面（误差） 与滑模面的导数 的曲线如图4所示。图中，虚线代表在有一定偏差的情况下，曲线逐渐趋近于滑模面 情形，实线为趋近过程实际值与期望值的误差。从图中可以看出，趋近曲线在滑模面 附近出现颤振现象。经分析，所采用的趋近律可写成：

。 （26）

从公式可以看出，趋近曲线在零点附近切换（不连续），只有在 时， 。由于Simulink仿真是将连续系统离散化，所绘制的图形受仿真步长的影响，此过程类似实际控制系统中开关器件及继电器的非理想特性，使趋近过程出现颤振。

图4 指数趋近律下的趋近曲线与误差

图5 改善趋近律下的趋近曲线与误差

为削减颤振，用饱和函数 代替上述控制律中的符号函数[13-14]。使控制输入修正到厚度为 的薄边界层中。即

。 （27）

此时，趋近曲线与误差曲线如图5所示。图中虚线为趋近曲线，在进入误差带后，趋近斜率由原来的 变化为 ，有效避免了 附近不连续造成的抖动。图中实线为趋近过程的误差曲线，可以看出，误差颤振现象得到有效抑制，甚至消除。

3 仿真分析

在Matlab/Simulink中对非线性动力学模型和设计的控制器进行仿真计算，为油气悬架车辆模型参数见表1。采用所设计的控制器调节油气悬架车身高度，得出车身位移、轮胎位移、控制阀芯电流、气室和作动器压力、功率消耗的仿真结果，如图6～10所示。

图6 车身位移

表1 油气悬架模型参数

参数 值

簧载质量 /

非簧载质量 /

轮胎刚度 /（N·m-1）

减振器阻尼 /[N/（m·s-1）]（

体积弹性模量 /

作动器初始压力 /

作动器初始体积 /

活塞面积 /

阻尼阀等效阻尼系数 /[Pa/（m3·s-1）]（）

气室初始压力 /

气室初始体积 /

气体多变指数 /

阀系数 /（ ）

低压源 /

高压源 /

摩擦力参数 /

摩擦力参数 /

摩擦力参数 /（s·m-1）

摩擦力参数 /（s·m-1）

摩擦力参数 /（N/（m·s-1））

20

图7 轮胎位移

图6所示 为系统车身位移（单位为 ）。结果表明，在考虑执行元件动力学特性和轮胎刚度的情况下，车身的实际位移可以较好地跟踪所期望的位移。无论车身升起或降落，跟踪过程较迅速、平稳。

图7所示 为轮胎垂向位移（单位为m）。结果表明，当期望车身高度为方波信号时，由于轮胎刚度的影响，作动器瞬间产生的较大压力会对轮胎产生冲击，迫使轮胎变形。轮胎变形会对车高调节的快速性和稳定性产生一定的影响。

图8所示 为控制伺服阀阀芯的电流（单位为 ）。结果表明，电流轮胎刚度会对控制系统造成一定的影响。当给车身期望的输出位移时，误差有较大突变，使控制电流瞬间达到最大值。由于作动器与气室油液的交互以及轮胎刚度的影响，使控制电流有些微小的振荡。当忽略轮胎刚度对悬架系统的影响时，电流基本无振荡。在1 s左右，电流归于0 A。车身在上升/下降过程中，电流基本保持正/负值。控制过程中，无过多能量耗散。车身逐渐趋近到期望位置时，电流为0 A。

图8 伺服阀电流

图9所示 、 为作动器及气室的压力（单位为 ）。结果表明，气室压力紧随作动器压力，两者变化趋势一致。符合油气弹簧的压力变化特点。

图9 作动缸与气室压力

图10所示 为车身高度控制过程的功率消耗（单位为W），可表示为

。 （27）

结果表明，由于轮胎刚度的影响，使系统功率消耗增大。车身位移上升时，通过液压泵使油液压入作动器，流量为正，所以功率消耗为正值；车身位移下降时，依靠车身重力及气室压力使油液压回油箱，流量为负，所以功率消耗为负值。功率消耗与车身位移调节时间直接相关，实际工程中，可以根据需要，通过调节相关参数，增大/减小车身上升/下降的时间，使功率增大/减小。

图10 功率消耗

4 结论

本文对油气悬架建立非线性化模型，并针对悬架特性设计积分分离PID与滑模控制结合的力跟踪控制方式，对非线性悬架模型在给定期望车身位移的条件下进行仿真。仿真结果表明，采用力跟踪方式构建的悬架模型能够有效跟踪给定的期望位移，并且在调节过程中，车身较为平稳、迅速。

本文研究单轮系统的车高控制，后续研究中将对半车及整车的姿态控制进行研究。

参考文献

[1] CAMPOS J，DAVIS L，LEWIS F L，et al. Active Suspension Control of Ground Vehicle Heave and Pitch Motions [C]// Proceedings of the 7th IEEE Mediterranean Conference on Control and Automation，Haifa，Israel，June 1999：

222–233.

[2] METZ D，MADDOCK J. Optimal Ride Height and Pitch Control for Championship Race Cars [J]. International Federation of Automatic Control，1986，22（5）：

509 -520.

[3] AKAR M， KALKKUHL J C，SUISSA A. Vertical Dynamics Emulation Using a Vehicle Equipped with Active Suspension [C]// Proc. of the IEEE Intelligent Vehicles Symposium， Istanbul，

Turkey， 2007：13-15.

[4] 陈志林. 基于变结构与PID联合控制策略的车身高度控制仿真 [J]. 清华大学学报（自然科学版），

1999，39（8）：72-75.

Chen Zhilin. Simulation of Variable Structure Control Strategy in Combination with PID for Vehicle Body Height [J]. Journal of Tsinghua Un iversity（Natual Science），1999，39（8）：72-75.（in Chinese）

[5] KIM H，LEE H. Height and Leveling Control of Automotive Air Suspension System Using Sliding Mode Approach [J]. IEEE Transactions on Vehicular Technology，2011，

60（5）：2027-2041.

[6] YAMASHITA M，H Control of an Automotive Active Suspension [C]//Proceedings of the 29th Conference on Decision and Control，Honolulu，

Hawaii，December 1990：2244–2250.

[7] ALLEYNE A， HEDNCK J K. Nonlinear Adaptive Control of Active Suspensions [J]. IEEE Trans. Control Syst. Technol，1995，3（1）：94-101.

[8] KNORN F. Modelling and Control of an Active

Hydropneumatic Suspension [D].

Otto-von-Guericke-Universit?t Magdeburg，2006.

[9] 庄德军. 主动油气悬架车辆垂向与侧向动力学性能研究 [D]. 上海：上海交通大学，2006.

Zhuang Dejun. Study on Vertical and Lateral Dynamic Performances of Vehicle with Active Hydropneumatic Suspension [D]. Shanghai：Shanghai Jiaotong University，2006. （in Chinese）

[10] GURAN A. Dynamics with Friction Modeling， Analysis and Experiment Part II [M]. London：

World Scientific，2001.

[11] 刘金琨. 先进PID控制 [M]. 北京：电子工业出版

社，2004.

Liu Jinkun. Advanced PID Control [M]. Beijing：Publishing House of Electronics Industry，2004. （in

Chinese）

[12] SLOTINE J J E.Sliding Controller Design for Nonlinear Systems [J]. International Journal of Control，1984，40（2）：

421–434.

[13] KIM K J. Chattering Free Sliding Mode Control [C]//SICE-ICASE International Joint

Conference，2006：18-21.

[14] SLOTINE J J E，Li Weiping. Applied Nonlinear Control[M].

USA：Prentice-Hall，1991.

作者介绍：

责任作者：柯欢欢（1989-），女，黑龙江龙江人。硕士研究生，主要研究方向为车辆悬架系统动力学及控制。

Tel：15300231539

E-mail： kehuanshine@163.com

通讯作者：管继富（1966-），男（汉族），黑龙江绥滨人。博士，副教授，硕士生导师，振动与噪声控制研究所副所长，主要研究方向为控制理论与控制工程、车辆悬架系统动力学及控制。

Tel：18511022850

E-mail： guanjifu@bit.edu.cn