基于集员未知输入观测器的风力机桨距执行器故障诊断
范小敏,章 伟
(上海工程技术大学 机械与汽车工程学院,上海 201620)
风力发电规模越来越大,风力发电技术也日趋成熟。但风力机一般安装在环境恶劣地区,桨距执行器极易发生故障。当风力机的桨距执行器出现泵磨损、液压泄露时,故障动态特性变慢,产生时滞。桨距执行器出现阀堵塞或泵堵塞时系统容易失控[1],维修成本高且复杂。目前国内外学者研究的重点是在风力机发生严重故障之前及时预测其破坏趋势,并对风力机的运行做出相应的调整,避免破坏的进一步扩大[2]。 由于气动、机械等方面的机理复杂,大型风力机建模非常困难[3-4]。现代系统辨识理论的发展为建立风力机系统模型提供了一条有效途径。在某一工况点附近采集系统的输入输出数据,应用随机系统辨识的方法,即可获得系统的辨识模型[5]。这种辨识模型是对风力机这样有较强随机扰动的线性系统建模的有效方法之一。
故障诊断技术作为提高系统安全性和可靠性的有效途径,受到了很多学者的广泛关注。目前故障诊断方法可以分为基于解析模型的方法、基于知识的方法和基于信号的方法[6-11]。基于解析模型的故障诊断方法应用在液压变桨距系统时一般采用观测器技术,将观测器的输出值和实际输出值对比产生的偏差作为残差信号判断系统是否发生故障[12-13]。风力机长期运行在沙漠等环境,容易受到未知干扰和噪声的影响,传统基于解析模型的故障诊断大部分假设噪声和干扰符合统计特性,但通过先验知识来获得实际系统的统计特性比较困难。集员估计是一种只假设系统的噪声和干扰未知但有界的状态估计方法,被广泛应用于故障诊断方面[14-18]。考虑到未知干扰和噪声,本文提出基于中心对称多胞体的未知输入观测器(Unknown Input Observer,UIO)的方法来诊断桨距执行器故障。首先,根据气动机理和现代参数辨识方法建立风力机模型,并通过设计未知输入观测器解耦干扰[19-21]。 然后,在满足系统匹配条件的前提下,对单一执行器故障设计一组未知输入观测器,使某个未知输入观测器对特定故障解耦,但对其他故障敏感。在不考虑执行器故障时,对未知输入观测器产生的残差采用中心对称多胞体生成残差区间的最大包络,将该包络区间作为动态阈值。 最后,基于一组集员未知输入观测器设计故障诊断策略。本文提出的方法结合了未知输入解耦和集员估计的优点,能够在干扰和噪声分布未知时实现故障检测与分离,并保证零误报率。通过对风力机桨距执行器模型发生突变故障和缓慢时变故障的仿真验证了所提方法的有效性。
1 风力机桨距模型描述
风力机系统由空气动力子系统、传动子系统、桨距子系统和功率子系统组成,可将风能转化为电能输出[11]。在一定的假设条件下,通过考虑和不考虑机械传动装置柔性,可以分为系统的3阶和5阶机理模型。
1.1 刚性传动风力机桨距模型的建立
1.1.1 空气动力子系统模型
(1)
(2)
Pr=Trωr
(3)
式中,ρ为空气密度;R为风轮转子半径;vr为有效平均风速;叶轮以转速ωr旋转,从而将风能转化为机械能;所转化的效率由功率系数Cρ(λ,β)决定;功率系数Cρ(λ,β)是叶尖速比λ和桨距角β的函数;Pr为风轮输出功率。
1.1.2 传动子系统模型
(4)
TD=C3ωr+C2/ωr+C1
(5)
次传动轴运动方程为
(6)
Tsωrη=Tmωg
(7)
其中,Jr和Jg分别为风轮的转动惯量和功率发生器的转动惯量;Ts为风轮轴扭矩;TD为风轮阻力扭矩;Tm为传动齿轮动扭矩;Tg为功率发生器反扭矩;η表示齿轮箱转动效率;C1~C3是对应的系数;ωg表示功率发生器转速。
风轮转速用一阶系统来描述
(8)
ωg=αωr
(9)
其中,Tω和ωc分别为时间常数和测量风轮转速;α为齿轮传动比。
1.1.3 电机子系统模型
功率系统能够将机械能转换成电能并输送给电网。本系统以功率发生器来代替水平轴风力机发电机,这里不考虑功率发生器扭矩和转速之问的动态特性,假设它们之间为线性关系为
Mg=Kgωg+Cg
(10)
其中,Kg和Cg分别为对应的系数。
1.1.4 桨距执行器子系统模型
单个桨距执行器可以建模为一个传递函数,以桨距角参考值βr为输入,并以桨距角β为输出,传递函数模型可以表示为
(11)
其中,ωn和ζ分别为桨距执行器的自然频率和阻尼系数。
1.1.5 刚性传动子系统模型
在上述建立的风速和气动参数关系的基础上,仍然选取风速作为模型中的调度变量,选取桨距角参考值作为控制输入,考虑扰动输入风速,记u=[βr,vr]T。选取发电机的速度和发电机转矩作为观测输出y=[ωr,Ts]T。同时考虑系统干扰和建模不确定性等未知干扰d∈Rnd和噪声w∈Rnw以及系统的状态变量x=[β,ωr,ωc]T,结合式(1)~式(11),可以得到风力机模型

(12)


1.2 柔性传动风力机桨距模型的建立
1.2.1 能量传递装置子系统模型
以ε代表次传动轴的相对位移角,有如下运动方程
(13)
(14)
Tε=104(100ε3-20ε2+2ε)
(15)
(16)
电机转速用一个一阶传感器来衡量
(17)
其中,k是联轴器的阻尼;转矩Tε是作用在次传动轴的静轴向转矩;ωm为测量输出电机转速;Tϖ为传感器时间常数。风轮转速可以由式(18)求得。
(18)
1.2.2 柔性传动风力机模型
风力机的状态方程如(12)所示,其中
(19)
D为零矩阵,A、B、C参数为:
2 改进的未知输入观测器设计
2.1 问题描述
不考虑未知输入时,对上述风力机模型离散化,进而得到下列离散线性系统形式

(20)
其中,x(k)∈Rnx、y(k)∈Rny、u(k)∈Rnu分别为状态向量、控制输入向量和测量输出向量;A∈Rnx×nx、B∈Rnx×nx、E∈Rnx×nx、C∈Rnx×nx为系统矩阵。
针对式(20)所示系统,设计的观测器如下

(21)

利用集员估计方法可以得到无故障发生时各个残差分量的包络,并且将该包络作为动态阈值。 中心对称多胞体可用于界定残差的上下界,相关的定义和性质如下文所述。
定义1r阶中心对称多胞体实际上是r维单位立方体的仿射变换,即

(22)

X⊕Y={x+y:x∈X,y∈Y}
(23)
性质1中心对称多胞体1=c1⊕Br的闵可夫斯基和也是一个中心对称多胞体。

(24)


(25)
在不失一般性的前提下,对式(20)所示系统提出了如下假设:
假设1不考虑功率发生器扭矩和转速之问的动态特性;
假设2系统参数矩阵C和参数矩阵E满足rank(C)=rank(CE);
假设3检测对(C,A1)可观,其中
A1=A-E[(CE)TCE]-1(CE)TCA
(26)
假设4干扰向量d(k)∈〈0,Ind〉是峰值为1的随机向量;
假设5系统的测量噪声和状态估计的初值满足下式
w(k)∈W=〈0,Φ〉,Φ∈Rnx×nx
(27)

(28)
2.2 干扰解耦
本文通过重构干扰矢量消除未知干扰的影响。重构干扰项必须满足条件rank(C)=rank(CE),若存在矩阵M,使得
MCE=Ird×rd
(29)
由此可得,d(k)的估计值为

(30)
对观测器进行干扰项的补偿,可以得到观测器的表达式为
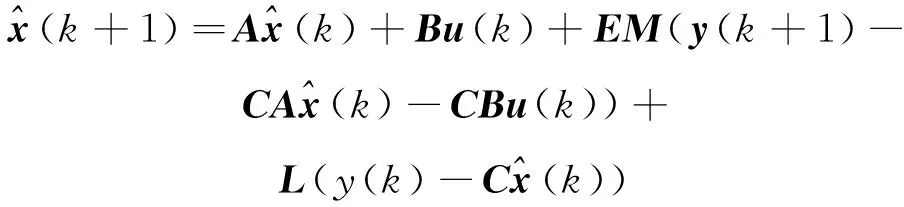
(31)
引入新的矩阵矢量来消除y(k+1)。

(32)
针对上述风力机模型,设计下列改进未知输入观测器

(33)
其中,TA-LC=N;TB=G;EM=H;L为极点配置计算出的观测器增益矩阵。在假设3成立时,使式(33)的N稳定,此时系统矩阵满足(I-HC)=E。
3 基于中心对称多胞体的阈值生成算法
从观测器的设计过程可以看出,不考虑系统噪声时,可以通过干扰重构达到干扰解耦的效果。但在风力机系统的实际运行中,噪声和干扰同时存在。考虑到噪声和干扰,风力机的状态空间方程为

(34)
定义状态估计误差向量为

(35)
系统发生故障时的离散线性系统形式如式(36)所示。

(36)
基于集员估计的方法能够给出区间估计结果,可作为故障诊断的动态阈值,是一种较为自然的残差评价方法。基于中心对称多胞体的集员估计是利用中心和边界生成矩阵,通过不断迭代估计每一时刻的残差中心估计值及边界,并以此作为阈值来进行故障检测。为此,本章节研究了基于中心对称多胞体的阈值生成算法。
针对式(36),通过设计一组集员未知输入观测器进行故障检测与分离,把第i个执行器故障记为未知输入。设计的未知输入观测器要保证第i个观测器生成的残差与其他所有的执行器故障尽可能敏感,并对第i个执行器故障解耦。
设计的一组未知输入观测器形为
(37)

Ni=TA-LiC
(38)


(39)

(40)
证明过程如下:
根据式(29)~式(35),由式(24)和式(25),生成的估计误差集合为
(41)
第i个未知输入观测器生成的残差ri(k)的中心对称多胞体为
(42)
通过上述推导过程,可以求出k+1时刻的状态误差及残差包络。



(43)

(44)
所以在无故障情况下,残差应满足
(45)
进而由中心值和生成矩阵生成每一时刻的残差分量的区间包络。
4 故障检测与分离策略
单个执行器故障时的故障诊断原理如图1所示,在单一执行器故障时,设计一组集员未知输入观测器,使得某个未知输入观测器仅对特定的执行器故障解耦而对其他执行器故障敏感。通过中心对称多胞体生成不考虑故障时未知扰动的最大包络,并将其作为阈值。没有故障发生时,所有的残差在对应的包络内;当第i个执行器发生故障时,第i个未知输入观测器对第i个故障解耦,其他观测器均受故障影响。因此第i个未知输入观测器生成的残差均在对应的中心对称多胞体,其他观测器生成的残差超出对应的中心对称多胞体。

图1 故障诊断原理示意图Figure 1. Schematic diagram of fault diagnosis
(46)

故障检测与分离策略如下:

(2)故障分离。当第i个未知输入观测器生成的残差分量均在中心对称多胞体范围内,而其他未知输入观测器生成的残差分量均有超出相应的包络范围,表明第i个执行器发生故障,实现故障分离。
5 仿真结果
应用文献[4]中辨识机理和推导的机理模型。风力机的仿真参数如表1所示。

表1 风力机仿真参数
5.1 三阶模型



选取


假设d(k)∈〈0,Ind〉,w(k)∈〈0,Inw〉分别为未知但有界的干扰向量和噪声向量。
情形1执行器2在k=50时发生突变加性故障,具体表达形式如下
(47)
为了保证系统故障是可分离的,在系统矩阵满足rank(C)=rank(CF)前提下,选取合适的极点,利用MATLAB工具箱进行极点配置,可求得观测器的增益矩阵Li的值。此时Ni的所有特征值稳定,待设计矩阵Ni为。
未知输入观测器i(i=1,2) 针对突变故障生成的残差分量及故障诊断结果如图2和图3所示。其中,水平实线为生成的实际残差分量,水平虚线为相应的中心对称多胞体的上下包络,x轴为迭代次数,垂直于x轴的虚线代表故障检测时间。图2中有残差分量超出相应的残差包络,说明执行器发生了故障。图3中所有残差均在相应的包络内,表明由于未知输入观测器2对第2个执行器故障完全解耦,生成的残差均不受故障影响,由此实现了故障分离。由仿真结果可知故障检测时间和故障分离时间为td=ti=50。

图2 三阶系统模型的UIO1所得的突变故障诊断结果Figure 2. Abrupt fault diagnosis result obtained by UIO1 of the third-order system model

图3 三阶系统模型的UIO2所得的突变故障诊断结果Figure 3. Abrupt fault diagnosis result obtained by UIO2 of the third-order system model
情形2假设执行器1发生缓慢时变故障的具体表达形式为
(48)
图4和图5分别为三阶系统UIO1和UIO2针对缓慢时变故障生成的残差分量及诊断结果。UIO1对第1个执行器故障完全解耦。利用所提出的故障检测与分离策略可以较快速地实现故障检测与分离,并能在较短的时间内检测出微小故障。

图4 三阶系统模型的UIO1所得的缓慢时变故障诊断结果Figure 4. Slow time-varying fault diagnosis result obtained byUIO1 of the third-order system model

图5 三阶系统模型的UIO2所得的缓慢时变故障诊断结果Figure 5. Slow time-varying fault diagnosis result obtained by UIO2 of the third-order system model
5.2 五阶模型
在考虑机械转速装置为柔性的前提下,得到的参数结果如下:
A=

选取
极点配置后得到Ni为

图6 五阶系统模型的UIO1所得的突变故障诊断结果Figure 6. Abrupt fault diagnosis result obtained byUIO1 of the fifth-order system model

图7 五阶系统模型的UIO2所得的突变故障诊断结果Figure 7. Abrupt fault diagnosis result obtained by UIO2 of the fifth-order system model
五阶风力机系统中,由未知输入观测器i(i=1,2)针对式(47)所示的突变故障生成的残差分量及故障诊断结果,分别如图6和图7所示。图6说明执行器发生了故障。图7中所有残差均在相应的包络内,表明由于UIO2对第2个执行器故障完全解耦,故实现了故障分离。
图8和图9分别为未知输入观测器i(i=1,2)针对式(48)所示的缓慢时变故障生成的残差分量及诊断结果。图9表示系统有故障发生,图8说明UIO1对第1个执行器故障完全解耦。

图8 五阶系统模型的UIO1所得的缓慢时变故障诊断结果Figure 8. Slow time-varying fault diagnosis result obtained byUIO1 of the fifth-order system model

图9 五阶系统模型的UIO2所得的缓慢时变故障诊断结果Figure 9. Slow time-varying fault diagnosis result obtained byUIO2 of the fifth-order system model

图10 文献[18]所得的突变故障诊断结果Figure 10. Result of abrupt fault diagnosis obtained inreference [18]
为了验证本文所提方法的优势,下文将文献[18]中不使用集员估计的方法与本文的方法进行对比。文献[18]是基于未知输入解耦设计一组滤波器,但使用了非集员方法。由于非集员方法的过程干扰和测量噪声是高斯分布,而本文所研究的系统是未知但有界的,所以假设其边界值为3φ(φ为过程干扰和测量噪声的标准差),由此近似计算出方差矩阵。仿真参数设置与情形1相同,使用文献[18]方法所得的仿真结果如图10所示。图10中实线代表滤波器残差的模,可以看出在t= 0.45 s前后,残差变化较大,很难人为设定残差阈值,凭个人经验选取阈值可能会引起故障。
6 结束语
本文针对一类含有未知但有界干扰和噪声的风力机系统的桨距执行器故障问题,设计了一种将未知输入观测器和中心对称多胞体结合的故障诊断方法。首先引入一组新的矢量矩阵进行干扰重构,优化未知输入观测器设计。基于中心对称多胞体计算未知输入观测器在无故障时对未知扰动产生的残差包络,并以此作为残差估计的阈值。 相对于文献[18]中的方法,本文提出方法的优势在于可以避免人为选取阈值的缺陷,在自动生成故障诊断的残差阈值的同时可保证零误报率。由仿真结果可以看出,本文提出的方法将未知输入观测器与中心对称多胞体结合,所设计的残差生成器的鲁棒性更强,能够更好地抑制噪声,同时可以更好地隔离干扰。对突变信号和缓慢时变信号的仿真也证明了所设计的观测器可以达到将不同的故障信号进行故障检测与分离的目的。但基于观测器的状态估计具有保守性,在故障诊断的过程中进一步减小状态估计的保守性和降低故障漏检率还有待进一步研究。

