PC三电平逆变器电解电容故障特征分析
王 新,黄 冲,许 翔
(河南理工大学 物理与电子信息学院,河南 焦作 454000)
随着现代化工业的快速发展,性能优异的中点钳位(Neutral Point Clamped,NPC)型三电平逆变器被广泛应用在中高压、大功率设备上。与传统的两电平逆变器相比,其可减少逆变器的电感值,减小体积,减少绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor,IGBT)损耗,且效率高。虽然NPC三电平逆变器具有很多优势,但是随着电容数量的增加,其发生故障的概率增加,稳定性有所降低。电容故障会使直流侧母线两电容电压值相差过大,从而导致直流母线充放电电压过大,造成中点电位的不平衡,损坏负载,降低电容的可靠性,使电容性能退化。
NPC三电平逆变器的主电路含有功率器件数量较多,而且其故障主要由内部器件失效造成的。目前,三电平逆变器故障研究多侧重于主电路的开关管故障[1-6],由于其故障特征比较明显,所以针对该类故障的研究较多。由电容参数退化引起的故障,由于其故障特征区分度差且不易诊断[7-9],目前的研究较少。
为解决电容故障特征难以提取的问题,本文在以上研究的基础上对输出电流信号进行预处理。本文构建电流偏差信号[10-13],进而对电流偏差信号进行变分模态分解(Variational Mode Decomposition,VMD)分析和处理,得到表征电容故障的特征分量,并计算其模态能量,最终提取电容参数性故障特征。本文提出的方法通过分析逆变器输出电流信号变化,可以判断出电容是否存在问题。
1 故障模式分析
NPC三电平逆变器拓扑结构如图1所示。在长时间工作过程中,电容C1、C2内部电解液会有不同程度的蒸发,导致其出现不同程度的老化。直流电压经两个等值电容C1、C2串联分压,形成两个电压源。电容C1、C2不同程度的老化会造成中点电压的不平衡,导致输出电压和电流畸变,严重时可能会破坏功率器件和用电设备。输出电流具有丰富的故障信息,可作为检测信号,所以本文选取线A相电流作为检测信号。

图1 NPC三电平逆变器拓扑结构Figure 1. NPC three-level inverter topology
本文选用电容类型为电解电容,两个电容标称值为3 300 μF,其中电容值减少10%以内可认为是正常情况。当电容量下降至初始值的60%左右时[14],一般视为电容的寿命终止。所以,本文根据常见情况,假定电容的退化范围为10%~30%,即分别为电容值退化到90%~80%和80%~70%。本文根据电容正常和退化程度,研究了单个退化和两个退化的故障模式,具体故障模式如表1所示。

表1 电解电容故障模式
2 基于VMD的故障信号分析与特征提取
2.1 VMD原理与算法步骤
2.1.1 变分问题的构造与求解
VMD的核心思想是构建和求解变分问题。假设把信号分解成K个分量,分解的分量要具有中心频率的有限带宽的模态分量,还要确保各个模态的估计带宽之和最小,其约束条件要保证所有模态之和与分解信号相等,约束表达式为
(1)
其中,μk为分解得到的K个IMF分量;ωk为中心频率。
求解上述(1)式变分问题过程中,可以通过引入惩罚因子α和拉格朗日乘子λ(t)将约束的变为问题变成非约束变分问题,得到增广拉格朗日表达式。
L({μk},{ωk},λ)=
(2)
利用乘法算子交替方向法结合Parseval、傅里叶等距变换,优化得到各个模态分量和中心频率,其各模态的频域更新计算式和中心频率更新计算式分别为式(3)和式(4)。
(3)
(4)
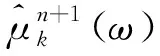
2.1.2 VMD算法步骤
VMD算法的实现步骤如下:
步骤1初始化μk、ωk、λ和n;
步骤2确定迭代次数;
步骤3根据VMD算法计算式更新μk、ωk;
步骤4根据相关算法更新拉格朗日乘数λ;

2.2 优化K值算法
VMD分解信号前,需要设定分解尺度因子K。K值决定了VMD分解得到的模态分量的个数。当K值较小时,出现欠分解现象,目标信号由于有更多的重要信息将不能被分解到有限带宽的模态分量中。当K值较大,会出现过分解现象,即同一个中心频率分量出现在多个有限带宽的模态分量中,对故障模式识别带来干扰。
为此,本文采用模态重复率来优化K值。模态重复率为[15]
(5)
式中,K为VMD的分解尺度因子;ωn为第K阶模态分量的中心频率;β取常数,本文取0.01。
从式(5)可以看出,经VMD分解后,若得到相邻两阶模态的中心频率不同时,因相邻中心频率差值较大,所以rn值将接近0。若得到相邻两阶模态的中心频率相同时,rn值会接近1/β。最佳的K值应选取各阶模态重复率之和接近0,且尽可能大。
2.3 信息熵
若存在一个随机序x(n)=(x1,x2,…,xn),取这n个值的概率分布为p=(p1,p2,…,pn)的信息熵为
(6)
对输出电流信号进行VMD分解,若分解得到的模态分量包含电解电容故障特征信息多,则会越有序,信息熵会越小。若模态分量包含电解电容中包含的故障信息越少,则会越无序,信息熵的值会越大。所以,可以通过计算各个模态分量信息熵的大小,来判断各个模态分量是否包含电解电容的故障信息,进而选择信息熵最小的模态分量进行故障分析[16-19]。
2.4 模态能量特征提取
对每一种故障模式下的故障电流信号进行VMD分解,得到若干个模态分量。依据上述方法选取想要的模态分量,进而计算模态能量。第i个模态分量的能量Ei为
(7)
式中,j为模态分量的数据个数;m为数据总数。
3 仿真实验与分析
在MATLAB/Simulink下,搭建图1所示的NPC三电平逆变器电路模型,其中逆变的工作频率为50 Hz,开关频率为20 kHz,电容初始值设为3 300 μF,信号的采样频率为200 kHz。由于仿真实验中变频器输出电流变化存在过渡过程,所以取输出电流稳定后的16 000个点作为样本。针对表1所示的故障模式,在每种模式下在电容值范围内设置10组C1和C2值,从而获取90组样本。
3.1 数据采集与分析
由表1可知,共有8种故障模式,故障模式较多。这里选取两个电容值正常的f0模式和两个电容值相差大的f22模式进行分析。各故障模式下归一化后的A相电流波形如图2所示。
从图2可以看出,以上两种电容故障模式的A相电流波形较为相似,难以提取并分析其故障特征。

(a)
3.2 故障样本集的构建
为了解决章节3.1中出现的问题,需要对A相输出电流进行预处理。为此利用归一化后电流检测值、电流参考值iref和高斯白噪声构建电流偏差信号er,用来构建故障样本集X。电流参考值如图3所示,其电流偏差信号[9-14]表示如下。
er=i-iref
(8)
故障样本集为X=(e1,e2,…,ei,…,en)T。考虑到实际电路中存在噪声,所以在电流偏差信号中加入信噪比为30 dB的高斯白噪声rn。

图3 电流参考值的波形Figure 3. Waveform of current reference value
以f0模式和f22模式构建的含噪声电流偏差信号如图4所示。

(a)
3.3 故障特征提取与分析
3.3.1 故障特征选取
(1)选取K值。以f0模式输出电流偏差信号为例,计算不同K值下的模态重复率r,计算结果如图5所示。

图5 不同K值的模态重复率Figure 5. Modal repetition rates for different K values
由图5可以看出,当K≤6时,模态重复率接近于0,说明没有出现模态混淆。当K>6时,模态重复率开始增加,说明出现过分解现象,即同一中心频率分量出现多个有限带宽固有模态分量。所以,当K取6时,分解效果最好;
(2)IMF的选取。选取尺度因子K为6, 惩罚因子为2 000,噪声容忍度设置为0,然后对输出电流偏差信号进行VMD分解。f0模式的偏差信号经过VMD分解的结果如图6所示。可以看出,f0模式的偏差信号被分解成6个IMF分量,利用信息熵对模态分量进行选取,筛选出敏感的IMF分量,保证了特征提取的可靠性。
图6中6个IMF的信息熵结果如表2所示,其中IMF1和IMF3的信息熵相差不大且都较小,所以选取IMF1和IMF3来进行故障分析,并将它们的模态能量之和ET,即ET=106(E1+E3),作为判断故障与否的依据。
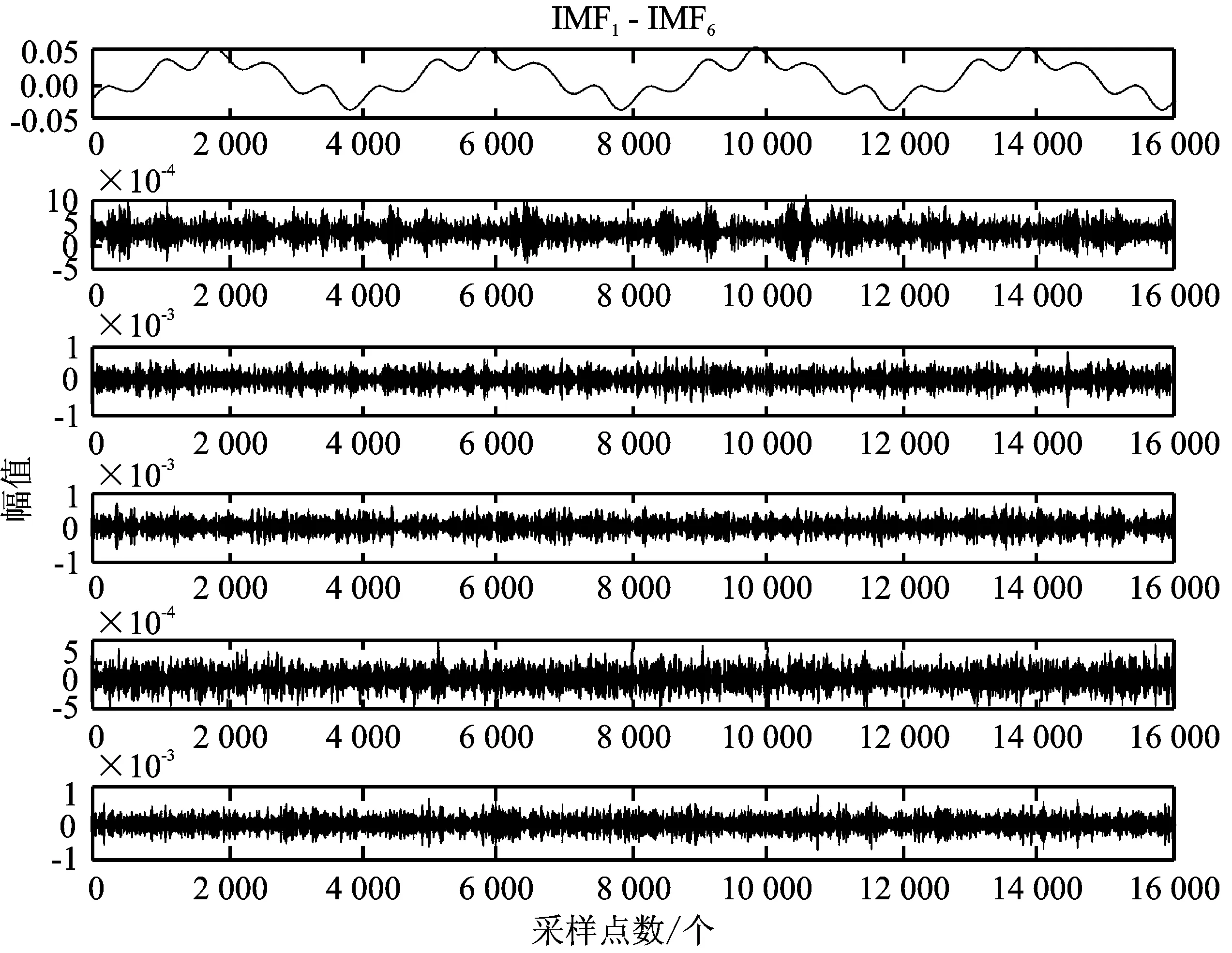
图6 f0模式输出电流偏差信号分解信号时域波形Figure 6.The output current deviation signal decomposition signal time domain waveform under f0 mode

表2 各IMF分量的信息熵
3.3.2 实验结果与分析
根据表1所示的1种正常模式和8种故障模式,在每种模式下,在电容值范围内设置10组C1、C2值,获取相应的10组电流信号,同时构建电流偏差信号作为故障样本集。按照上述方法设置VMD参数,计算出模态能量。鉴于篇幅原因,图7给出了f0、f31、f34的模态能量ET。表3为9种模式的模态能量ET区间范围。
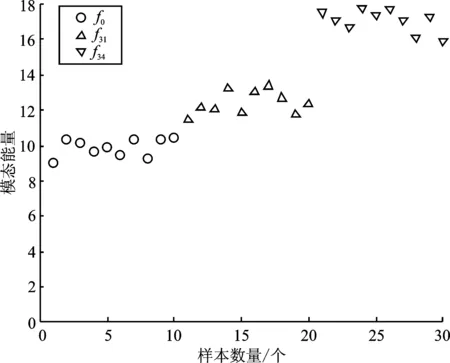
图7 不同模式下偏差信号模态能量Figure 7. Modal energy of deviation signal in different modes
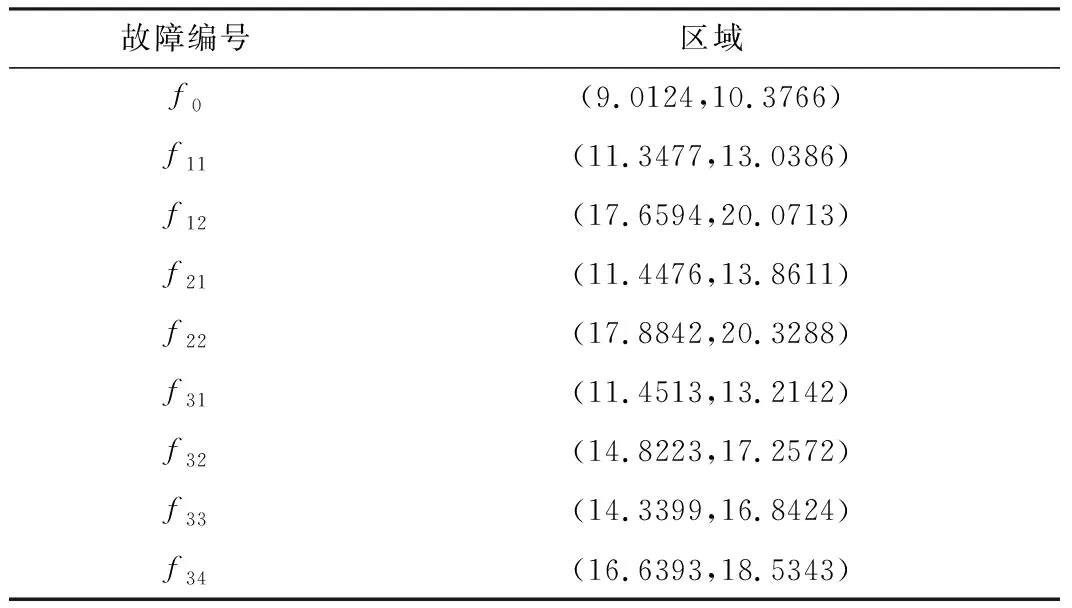
表3 不同故障模式模态能量区域
由表3和图7可得,电容退化情况下的模态能量与正常情况下的模态能量相比有明显变化。一侧电容正常时,模态能量会随着另一侧电容退化程度的增加而变大。当两侧电容同步退化时,模态能量也会随着电容退化程度增加而变大。
4 结束语
本文利用故障信息频率分布特点,采用模态重复率来确定VMD分解层数,利用信息熵对模态分量评价,能够准确筛选出含有故障信息敏感的IMF分量。为解决故障特征难以提取的问题,对输出电流信号预处理,通过设置电流参考值,构建电流偏差信号,组成故障样本集,使得故障特征更加明显,便于取得较好的分析效果。通过对各模式的电流特征分析,验证了模态能量法在提取电解电容退化故障特征方面的有效性,为今后对NPC三电平逆变器电解电容故障特征提取的研究提供了一定的理论依据。

