基于VW-IGRBF神经网络的出水BOD软测量
赵豆豆,张 伟
(河南理工大学 电气工程与自动化学院,河南 焦作454000)
生物需氧量(Biological Oxygen Demand,BOD)是反映水中有机污染物含量的一个综合指标[1-2]。目前通用的BOD测量方法的操作周期为5天,且无法在线测量,检测滞后、精度较低[3]。同时,在污水处理过程中,出水BOD影响因素反应机理复杂,具有非线性和不确定性等特点,难以建立机理模型。采用基于数据驱动的软测量建模方法[4]可避免精确数学模型建立问题,易于实现在线测量。
研究人员对出水BOD的软测量问题开展了大量研究。文献[5]建立了基于 PSO-ESN神经网络的污水处理软测量模型,并对污水处理关键水质参数 BOD进行预测。其仿真结果证明了该模型可有效预测污水处理过程中的关键水质参数,但模型的预测精度还有待提高。文献[6]应用卷积神经网络(Convolutional Neural Networks,CNN)模型,使用二维输入数据来预测污染负荷并评估CNN模型的适用性。结果表明,水文图像能够实现稳定的模型学习和泛化,但其收敛速度有待提高。径向基函数神经网络(Radical Basis Function,RBF)是一种性能良好的前馈型人工神经网络,其非线性映射能力较强,收敛速度快且不易陷入局部最小值。文献[7]建立了一种基于灰狼算法和RBF神经网络的污水处理模型,优化隐含层到输出层的权值,避免了过训练现象,实现了污水处理中出水BOD的预测。但该网络仅采用高斯函数作为激活函数,其表达和自适应能力较低,预测精度有待进一步提高。文献[8]提出了一种IErrCor算法,基于二阶的构造机构提高了结构的紧凑性和计算效率。最优初始参数加速了收敛过程,使IErrCor RBF网络更加稳定,但选择固定的宽度降低了网络激活函数的泛化能力。文献[9]提出一种基于递归正交最小二乘算法的结构设计方法,解决了递归径向基函数神经网络结构难以自适应的问题。该方法利用梯度下降算法更新网络的参数,并通过污水处理过程中关键水质参数动态建模等实验验证了结构设计方法的可行性和有效性。但神经网络参数学习算法不仅无法达到预期的效果,还影响算法运算精度。
针对污水处理过程中出水BOD难以精确测量的问题,本文提出一种基于变宽度的逆平方根和高斯函数组合的RBF神经网络(Variable Width RBF with Inverse Square Root and Gaussian Function,VW-IGRBF)的出水BOD软测量方法。将开口方向一致的高斯函数和逆平方根函数通过线性组合,获得新的隐层神经元激活函数,提高了函数表达能力和自适应能力。基函数的核宽度表征样本点对周围区域影响范围的大小,因此对模型的泛化能力有较大的影响。然而最优宽度的选择随训练变化有所不同,所以本文将引入变宽度策略来提升网络的泛化性能。同时,采用LM算法进行参数学习,控制参数随迭代步数动态改变,网络参数由滑动窗口动态调整。最后,通过实际污水处理过程BOD的数据仿真实验,验证其可行性及优越性。
1 相关工作
1.1 RBF神经网络
RBF神经网络的基本结构由输入层、隐含层和输出层构成[10-11]。定义X=[x1,x2,…,xI]为输入向量,H是隐含层神经元的个数,隐含层节点的激活函数φh(·)是一种局部分布且对中心点径向对称衰减的非负非线性函数。RBF神经网络通常采用高斯函数作为激活函数
(1)
其中,ch表示第h个隐节点的中心;b0表示隐节点的宽度,输出层的表达式为
(2)
其中,ωh表示第h个神经元到输出节点的连接权值。
1.2 BOD软测量辅助变量的选取
筛选辅助变量可以简化神经网络模型的输入,提高网络的预测精度。本文通过主元分析[12-13](Principal Component Analysis,PCA)降维,获得对出水BOD贡献值大的变量作为主要输入变量。首先将采集的样本数据进行归一化处理,然后将归一化后的变量按列组成原始数据矩阵X,得到X的协方差矩阵
(3)
COV(X)Pi=λIiPi
(4)
其中,COV(X)是X的协方差矩阵;I是样本数;Pi是协方差矩阵的特征向量;λIi是按照降序排列的特征值。
第i个主元的贡献率为
(5)
前a主元的累计贡献率为
(6)
前a个主元的累计贡献率超过85%时就认为反映了过程的主体信息。选择前a个主元作为VW-IGRBF神经网络的辅助变量,最终确定的10个辅助变量如表1所示。
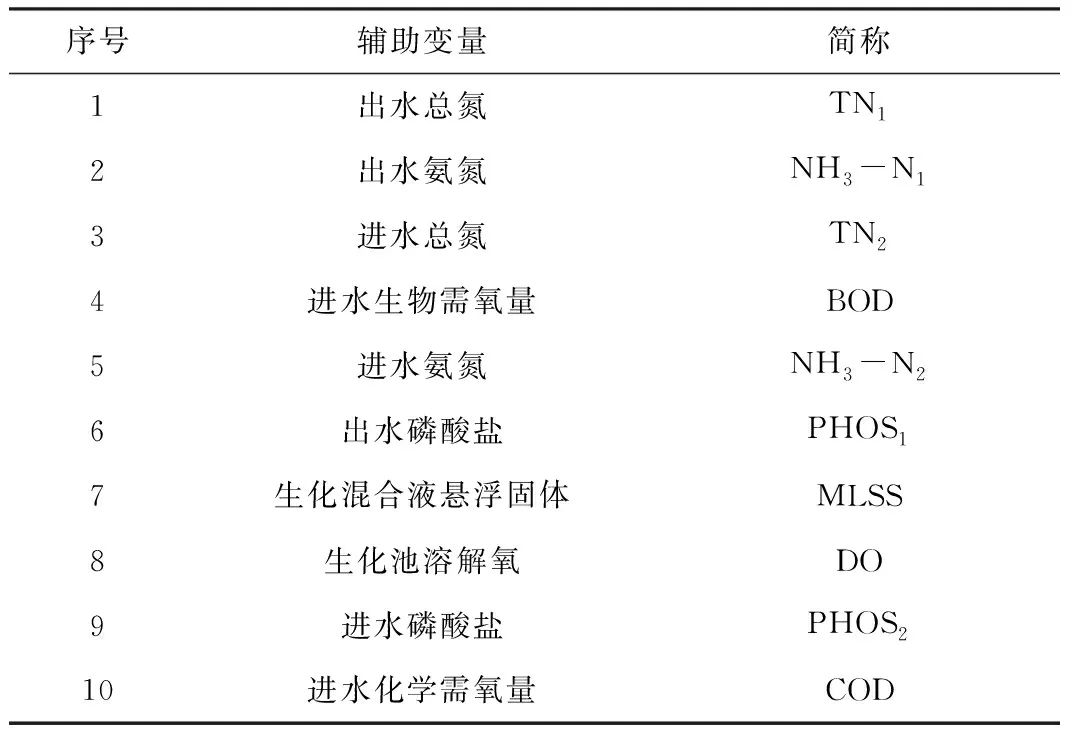
表1 选取的辅助变量
2 基于VW-IGRBF神经网络的出水BOD软测量
基于VW-IGRBF神经网络建立BOD软测量模型的整体结构如图1所示。

图1 VW-IGRBF结构Figure 1. The structure of VW-IGRBF
2.1 IGRBF神经网络
激活函数决定了样本对全空间的影响规则[14],不同激活函数对网络性能有不同影响。为了提高神经网络的逼近精度和泛化能力,考虑将具有不同表达能力的逆平方根函数和高斯函数通过线性组合的形式形成新的神经元激活函数。逆平方根函数和高斯函数开口方向一致,但具有不同的表达能力,两个函数在不同宽度下的函数值如图2和图3所示。对于常用的高斯函数,其在某些区间梯度接近于零,即函数饱和,导致参数无法继续更新。当宽度小于0.2时,高斯函数在[0.5,1]区间内的梯度接近于零,而逆平方根函数的梯度仍然存在。当激活函数的宽度为1时,逆平方根函数的梯度接近于零,而高斯函数梯度存在。为了避免出现单一激活函数在某些区间存在饱和现象的问题,并提高其表达能力和自适应能力,本文将逆平方根函数和高斯函数线性组合,以获得新的神经元激活函数。
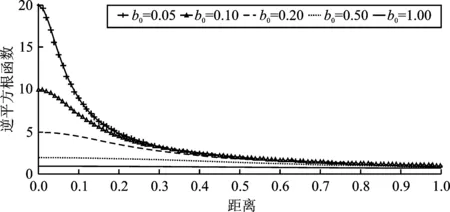
图2 不同宽度下的逆平方根函数Figure 2. The inverse square root function under different widths
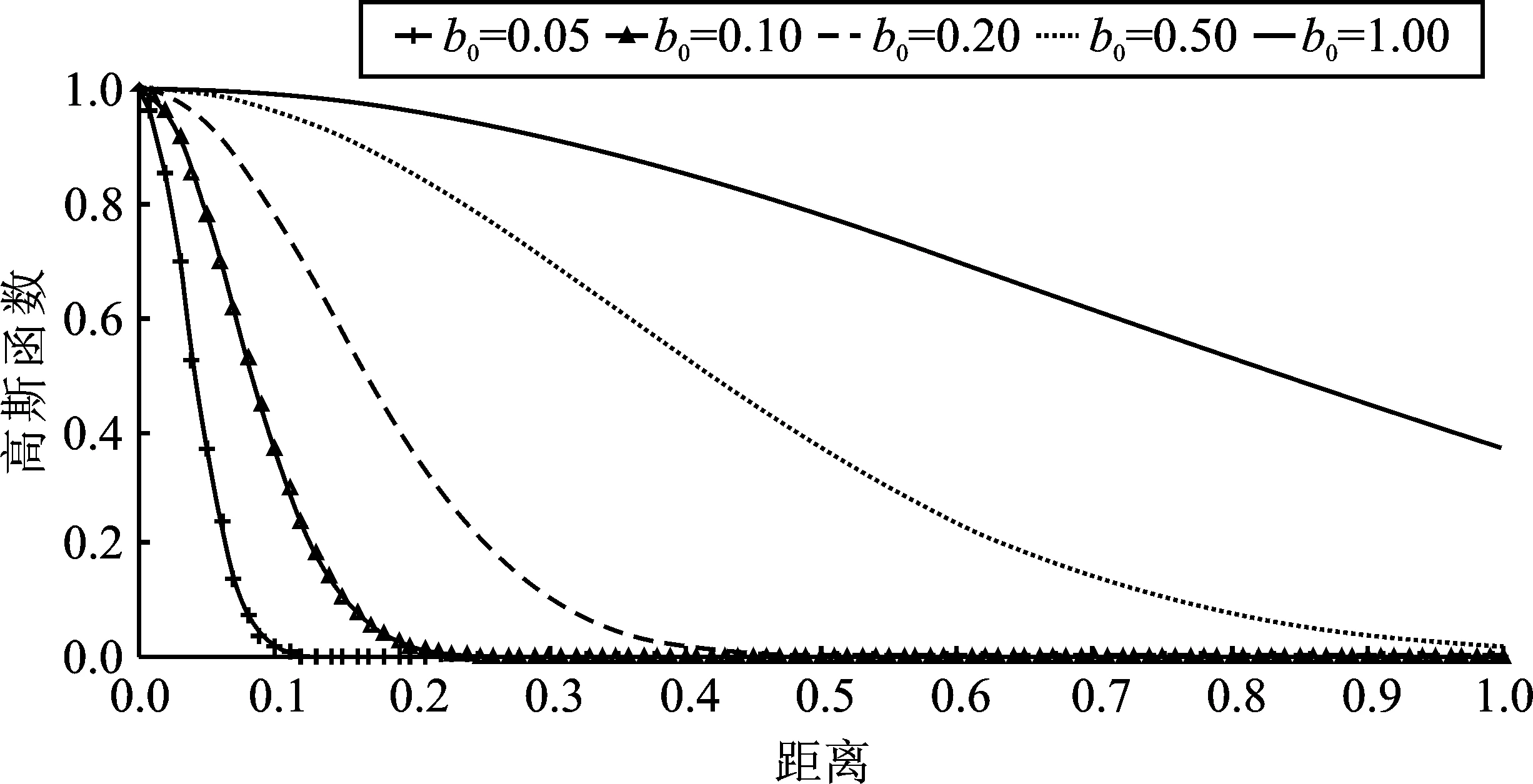
图3 不同宽度下的高斯函数Figure 3.Gaussian function under different widths
本文采用的逆平方根函数和高斯函数表达式分别如式(7)和式(8)所示。
(7)
(8)
由逆平方根函数和高斯函数线性组合的新的隐层激活函数可表示为
φh0(X,ch)=α1φh01(‖X-ch‖)+α2φh02(‖X-ch‖)
(9)
其中,α1是逆平方根函数的融合权重;α2是高斯函数的融合权重。
2.2 基于核密度的变宽度策略
一般情况下,数据在输入空间分布不均匀,由图2和图3可以看出,宽度对逆平方根函数和高斯函数均有较大影响。最优宽度的选择随训练的变化有所不同,固定宽度会导致过度平滑[15-16]。考虑到独立分布的随机变量的概率密度函数估计问题,在核密度估计中,宽度的选择很重要。本文引入基于核密度的变宽度策略来提高RBF神经网络的泛化能力。
定义局部密度表达式为
(10)
其中,b0是全局宽度;核函数K是一个以0为中心,积分为1的高斯函数;指数d是数据空间{xi},i=1,…,I的维度。局部宽度b(xi)更新为
(11)
其中,p(xi)是xi的估计密度;θ是灵敏度参数(0≤θ≤1,一般取1/2);λ是对局部宽度有影响的比例常数。
如果p(xi)<λ,b(xi)相对于b0增大,表示点xi更加平滑。如果p(xi)>λ,局域宽度变窄,令λ等于{p(xi)},i=1,…,I的几何平均数,可以写为
logλ=n-1∑log(p(xi))
(12)
将式(11)中b替换式(7)和式(8)中b0,则有
(13)
(14)
根据式(9),基于变宽度策略,新的隐层激活函数可表示为
φh(X,ch)=α1φh1(‖X-ch‖)+α2φh2(‖X-ch‖)
(15)
设网络第t个训练样本满足α1(t)+α2(t)=1,有
(16)
(17)
综合式(15)~式(17),可将VW-IGRBF新的激活函数定义为
φh(X,ch)=
(18)
VW-IGRBF对第t个样本输出为
(19)
定义网络期望输出与实际输出之间的误差为
e(t)=d(t)-y(t)
(20)
其中,d(t)是网络期望输出;y(t)是网络实际输出。
2.3 改进LM算法
LM算法是一种二阶算法,相比其它梯度下降法,该算法运算效率较快。训练VW-IGRBF时,采用LM算法进行参数学习,参数更新规则为[17]
Z(k+1)=Z(k)-[JtTJt+μ(k)E]-1JtTe(t)
(21)
其中,Z(·)表示VW-IGRBF中可调参数(包括VW-IGRBF隐节点激活函数的中心c、宽度b0、网络隐节点与输出节点的连接权值ω以及融合权重α1和α2);k为迭代步数;Jt表示Jacobian矩阵;μ(k)为组合系数,其作用是保证JtTJt+μ(k)E可逆;E为单位矩阵。
计算Jacobian矩阵第r行元素
(22)
其中,r表示RBF神经网络中的ω、c、b0、α1、α2这5个可调参数。记参数向量为
Z=[ω1…ωh…ωH,c1,1…c1,i…c1,I…ch,1…
ch,i…ch,I…cH,1…cH,i…cH,I,b01…b0h…b0H,α1,α2]
(23)
对于第t个训练样本,考虑RBF网络中可调参数ω、c、b0、α1、α2,则Jacobian矩阵中的行元素值为
(24)
在LM算法中,当控制参数μ的取值过大时,误差曲面梯度较小,算法类似于梯度下降法,收敛速度慢;反之,误差曲面梯度较大,算法类似于高斯牛顿法,容易导致式(21)不可逆,使算法失效。在训练初期,μ的取值应相对较小,后期μ的取值应相对较大[18]。
针对以上问题,为了提高算法的运算精度,使LM算法的控制参数μ随迭代步数动态地非线性增大
(25)
其中,μ1和μ2分别为μ的初值和终值;MaxItr为迭代步数;t为当前迭代步数。图4为MaxItr=500时μ随迭代步数变化的曲线。

图4 控制参数的变化曲线Figure 4. The change curve of control parameters
尽管目前 LM 算法在训练神经网络方面的效果较好,但其批处理的方式不适用于需要在线训练的非线性时变系统。神经网络进行在线学习时应尽量使用最新的一组动态样本对网络参数进行调节。为了解决这一问题,本文采用滑动窗口动态调节网络参数,实现LM算法在线进行。设滑动窗口是一个长度为L的队列,其所有样本都是VW-IGRBF中训练样本。当一个新样本产生后,窗口中最前边一个样本滑出窗口,最新的样本进入窗口[19]。
定义VW-IGRBF的学习目标函数为
e(L)=β(i)(d(i)-y(i))2
(26)
其中,d(i)和y(i)分别为窗口中第i个样本的期望输出和实际输出;β(i)表示遗忘因子,其表达式为式(27)。
(27)
2.4 VW-IGRBF神经网络的计算复杂度分析
与传统RBF神经网络相比,VW-IGRBF神经网络计算量较大,算法运行时间较长,但该算法在以下3个方面提高了网络性能:
(1)将开口方向一致的逆平方根函数和高斯函数线性地组合在一起形成新的隐含层激活函数,使激活函数能够融合两个不同函数的优点,有效提高了隐层激活函数表达能力和自适应能力;
(2)引入变宽度的方法,使核宽度随训练的变化而变化,保证高斯核之间的自然重叠,并有效提高网络基函数的泛化能力及预测精度;
(3)改进LM算法实现了算法的在线进行,使网络对学习参数的变化具有更好的鲁棒性并易于收敛。
3 仿真实验
本文所用数据来源于北京市某污水处理厂采集的样本数据,通过人工剔除异常数据后,得到360组数据,其中260组数据作为神经网络训练样本,100组数据作为测试样本。为验证所提VW-IGRBF方法的性能,分别采用RBF神经网络、IGRBF神经网络和VW-IGRBF算法对出水BOD进行预测。仿真实验基于MATLAB编程实现。
神经网络初始参数设置如下:隐节点个数H=15,训练步数为100,窗口长度L=50,控制参数μ初值μ1=0.1,终值μ2=1.0。设置IGRBF神经网络和VW-IGRBF神经网络中逆平方根函数和高斯函数的初始权重比例相同,即α1=α2= 0.5。
仿真测试结果如图5~图7所示。图5给出了3种算法的测试样本输出。图6给出3种算法的测试误差。图7为3种不同算法下绝对误差和相对误差的折线图。绝对误差反映预测值偏离实际数据的大小,相对误差指的是测试所造成的误差与实际数据之比乘100%所得的数值,能够客观地反映预测结果的准确度。
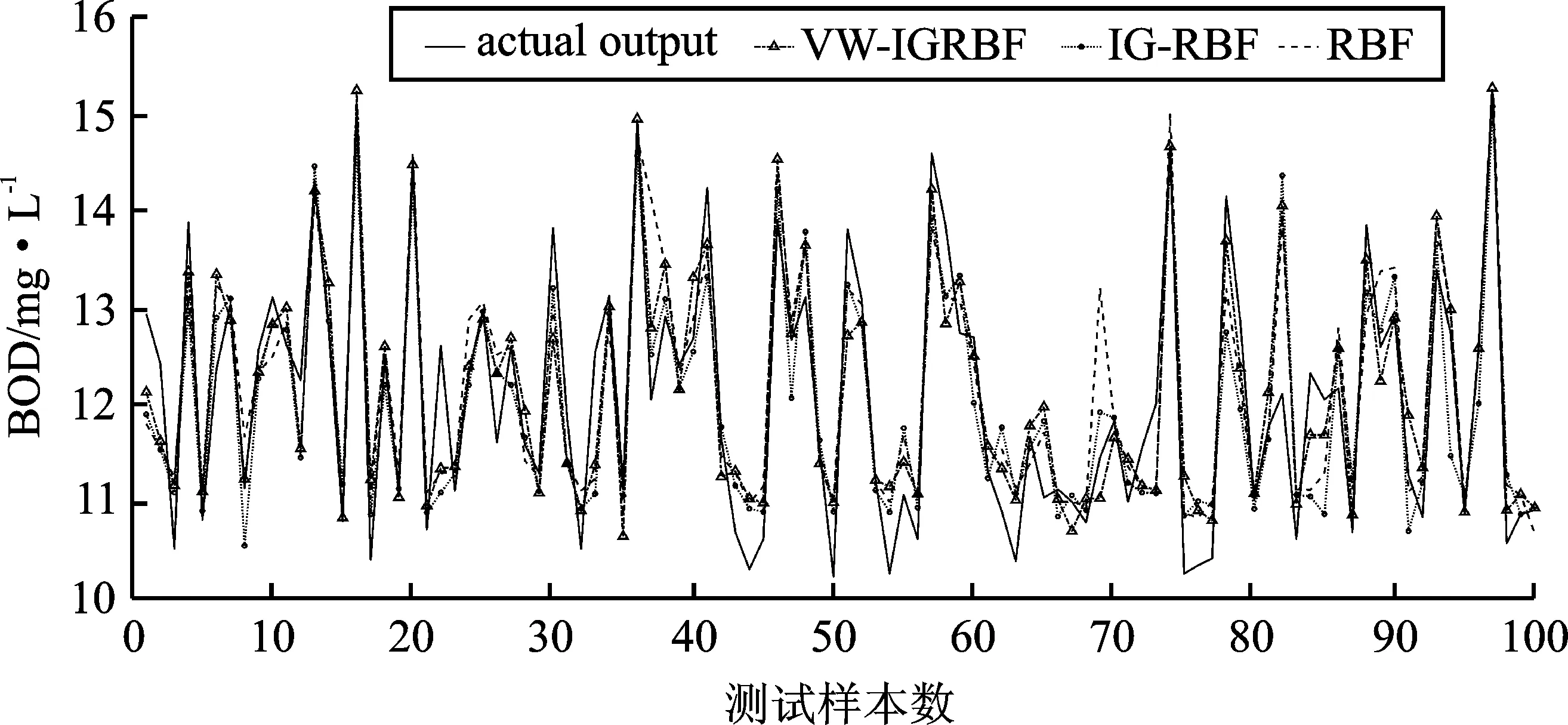
图5 测试样本输出Figure 5. The output results of test samples
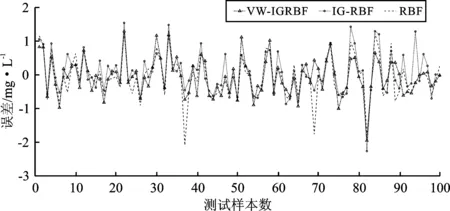
图6 测试样本误差Figure 6.The errors of test samples

图7 测试样本绝对误差与相对误差Figure 7. The absolute errors and relative errors of test samples
实际输出和3种算法输出之间的比较如图5所示。采用VW-IGRBF算法的BOD测试输出最接近真实输出,虽然有一些偏差,但相比其它两种算法,其拟合度较高。由图6可以看出,3种算法测试阶段的极大值处和极小值处的误差均在一个很小的范围,相对于RBF,IGRBF和VW-IGRBF的测试精度有所提高,VW-IGRBF存在个别测试样本误差较大,但多数情况下其误差均小于IGRBF。由图7可以看出,3种算法中,本文提出的VW-IGRBF的预测值与实际样本的偏离最小,准确度最高。以上结果说明激活函数采用逆平方根函数和高斯函数线性组合的形式使模型具有较高的软测量精度,引入基于核密度的变宽度策略可使模型具有较好的泛化能力。
表2为3种不同算法下方差、标准差及平均绝对误差(Mean Absolute Error,MAE)3种性能指标在10次随机实验中的平均值。标准差和方差越小说明数据越集中、越稳定,反之越离散。MAE避免了出现误差正负相抵消的情况,与平均误差相比,MAE能更好地反映预测值误差的实际情况。LM算法下的RBF、IGRBF和VW-IGRBF的各项性能指标均依次减小。在方差对比中,VW-IGRBF仅是RBF的80.9%,是IGRBF的86.8%。这些结果表明IGRBF中隐层激活函数采用逆平方根函数和高斯函数线性结合的方式,可以提高其表达能力和自适应能力。由二者线性结合的激活函数逼近能力要强于单个基函数,引入变宽度策略使网络激活函数有更好的泛化能力和更高的预测精度,有效验证了VW-IGRBF在出水BOD预测中的优越性。

表2 算法的性能指标
实验结果表明,在3种模型中,基于VW-IGRBF神经网络的出水BOD软测量模型预测精度较为突出,预测数据与均值的偏离程度以及预测数据的离散程度较小,更适合具有复杂非线性特性的污水处理过程出水BOD的软测量建模。
表3给出了VW-IGRBF与其它几个文献中提到算法的性能指标对比。由表可知,其它算法的测试均方根误差(Root Mean Square Error,RMSE)是VW-IGRBF的1.6倍以上,测试均方误差(Mean Square Error,MSE)是VW-IGRBF的2.7倍以上,VW-IGRBF的测试精度较其它算法有大幅度的提高,VW-IGRBF网络结构更紧凑,表明VW-IGRBF算法在很大程度上提高了出水BOD的测量精度。

表3 VW-IGRBF与其它算法的性能指标对比
4 结束语
针对污水处理过程中难以在线精确测量出水BOD的问题,本文将逆平方根函数和高斯函数通过线性组合获得新的神经元激活函数,避免了常用的高斯函数在某一区间出现饱和现象的问题,提高了激活函数的表达能力和自适应能力。本文采用基于核密度的变宽度策略,使宽度随训练的变化而变化,提高了网络激活函数的泛化能力。同时,采用LM算法进行参数学习,使控制参数随迭代步数动态非线性增大。本文还引入了滑动窗口动态调节网络参数,提高了算法的运算精度,实现了在线建模,使网络对学习参数的变化具有更好的鲁棒性并易于收敛。最后通过出水BOD仿真实验验证了本算法的优越性。仿真研究表明,VW-IGRBF出水BOD软测量模型适应非线性动态系统的能力较强,预测精度较高,适合污水处理过程中复杂非线性动态系统建模。

