一种基于最大化序列交互信息的延迟估计量化-检测算法

林丹楠

（福建商学院 信息工程学院，福建 福州 350012）

传感器网络已经成为监测不可访问环境的一种全新工具。它由小型、低功耗的无缆节点构成，这些节点集中部署在人们感兴趣的环境中，相互通信以实现目标感知。传感器网络运行的一般模型是从每个传感器采集有噪声的信号测量值，并在中央处理器或局部簇头进行融合，以估计出某些环境参数[1]。由于这些节点通过无线媒质进行通信，而且网络通常由大量的传感器构成，因此带宽就显得非常昂贵。尽管传感器配备了机载处理器和通信元件，但它们在功率、计算能力和内存方面都受到限制。文献[2]指出主要的功率损耗是无线电，通过比较计算和通信所需的能量，得出的结论是，只处理和传输所需的以及预处理数据，比发送原始数据更节省，并可延长系统的寿命。文献[3]中描述的传感器节点，通信所需能量为1nJ/bit，处理每通信比特可计算约150条指令。

在许多传感器网络任务中，定位查找是传感器网络的一个重要应用，而对不同传感器数据之间的时延进行估计又是定位的关键步骤，即时延估计是定位查找的前提，如声源定位。文献[4]研究了关于压缩信道的一般时延估计（当信道统计量未知时）问题。文献[5]提出由一组分布式传感器接收来自单个源的鸟叫声波形，在一个宏节点上收集这些波形并互相关联，以估计它们之间的时间延迟。这组时间延迟连同已知的传感器位置，然后就可以用来定位源。文献[6]描述了一种基于集群的协议，其中传感器节点将自己组织成本地集群，只有一小部分被选为集群头的节点将其本地集群中的数据聚合到基站。为提高多径条件下无线信道测量中的时延估计精度，文献[7]结合匹配滤波、方位估计方法以及基于加权傅里叶变换和松弛算法，提出了一种具有额外根的方位估计与基于加权傅里叶变换和松弛法算法的融合算法。新算法既可以分辨多径时延，又能很好地抑制噪声以及强干扰。文献[8-9]研究了当外围节点与中心节点通信的信息受到容量约束时，采用已知观察模型的中心站点的二进制判决问题，在给定虚警概率上限的情况下，漏判概率最小，研究的重点是优化渐近性能准则（观测值的渐近性）。文献[10-11]的研究指出，分类（多假设检验）误差概率的渐近界与几个假设之间成对距离的最小值有关。文献[5，12，13]研究了互相关检测器的非标准量化技术。文献[5]提出传感器数据用2-级量化器进行预处理，用其符号替换每个信号值。尽管这是一个简单的低速率编码器，但在噪声条件下，利用信号模型和可用带宽的量化方案将表现更好。这样的量化器有更多的量化级，允许更快地估计传输的样本数，这是跟踪应用中的一个关键优势。通过适当的熵编码，在某些情况下还可以转化为比特率方面的增益。文献[12]提出了一种基于变换的量化方案优化和一种基于Cramer-Rao 界（Cramer-Rao Bound，CRB）的用于时延估计的非MSE失真测量方法，先是对传感器数据进行块变换，然后对变换系数进行位分配，从而带来了额外的复杂性和处理延迟，且相关器输出依赖于量化器的再现级。文献[13]提出了一种用于互相关的量化器设计，它可以最小化量化相关函数和非量化相关函数之间的平方误差，但这仅是一个近似误差概率。

综上可知，在传感器网络中，感知数据之间的时延估计以及数据传输带宽、功率消耗和存储都是很重要的。对此，本文提出了一种分层处理体系结构和最大化两个接收序列之间的交互信息（Maximizes Mutual Information，MaxMI）的量化检测算法，它在每个延迟假设下计算接收波形间的经验交互信息，并选取最大值。实验结果表明，在中低信噪比下不仅有与非量化估计检测算法相媲美的性能，而且优于一般的基于量化数据与非量化数据之间的均方误差的标准标量量化检测算法。

1 问题构建

一般而言，分层处理体系结构通常可以在保持较高感知精度的同时大幅度减少网络流量。直接从多个传感器读数估计源位置而不经过中间延迟估计步骤是比较难的，而从两个传感器的延迟估计子系统到多个传感器系统的归纳相对简单。因此，本文着重研究估计两个传感器读数之间的延迟。

考虑两个传感器的情形，每个传感器捕获和传输同一信号的延迟和噪声样本，这种双传感器延迟估计系统如图1所示。传感器接收源波形的噪声和延迟数据，量化后被发送到融合中心（中央处理器），在那里计算延迟，任务就是估计接收波形之间的延迟D。对于两个传感器来说，其接收波形为

图1 双传感器时延估计系统构成

在用标量量化器Q（×）处理后，得到两个传感器的量化序列为，

我们的目标是设计一个量化-检测器系统，使得基于量化噪声形式的延迟估计值尽可能接近于基于原始信号的延迟估计值。

将源信号视为一个随机过程的实现，而非一个确定的波形，并假设在两个传感器上都有相同的量化器。如图1所示，为便于分析，过程x、w1、w2被建模为相互独立、零均值和白色的，具有已知的概率密度函数（Probability Density Functions，PDF）。我们估计每M个样本帧之间的延迟，这个延迟就是两个连续的M个样本之间滞后的样本数。假设未知随机参数D是一个位于已知范围[0，Dmax]内的整数，并且可以是这个范围内的任意值。

2 本文提出的算法

2.1 检测

互相关是计算两种波形之间延迟的最简单方法之一[14]。通过对离散估计的度量值和两个最接近的指标进行插值[15]，可以得到连续值的延迟估计。D的估计由无偏样本互相关峰值的滞后给出

在融合中心联合观测为高斯白噪声的假设下，表明基于相关关系的检测器是未知确定性源信号的广义似然比检验（Generalized Likelihood Ratio Test，GLRT）估计器（即渐近逼近最优极大似然检测器）。然而，这种假设在随机源的粗量化下是无效的。此外，求解这个检测器的最小误差概率的量化器是困难的，因为量化器的判决电平和再现值都会以非线性的方式影响相关器的输出。基于这种方案存在的不足，本文提出一种新的检测器，它利用量化数据的离散性，以及信号和噪声模型，这样会更合适。鉴于D的离散值假设，将延迟估计转换为一个假设检验问题，具有Dmax+1个选项。众所周知，给定一个假设检验问题，且误分类代价相等，则最大后验检验就是最小误差检验概率，于是可以构建出本文问题的多假设框架和相应的检测器。

设假设Hn（[0，Dmax]）对应于n为两个接收序列之间的真实延迟，令Z为中心检测器接收到的量化符号的完整集合

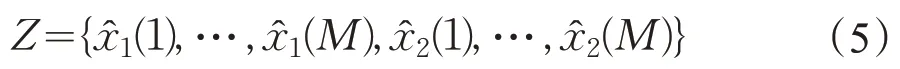
每个编码器的输出符号都是由一个有限的离散字母表生成的。对于L-级量化器，一种可能的编码器输出字母表是整数集0，…，L-1。当全部Hn等可能时，则MAP（Mean Average Precision，即各类别AP的平均值）检验为

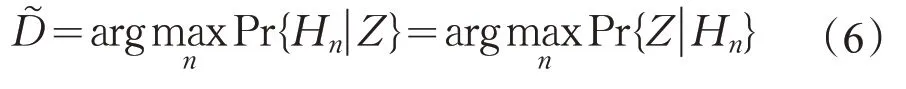
于是，寻找两个序列之间的延迟就可以简化为确定两个序列在最大似然意义上“匹配”得最好的偏移或延迟。

假设Hn等价于说法，一个量化序列中的每个符号对应于另一个序列中滞后n的符号（来自于与之相同的原始源输出），于是可确定以下结构的似然

采用标量或无记忆量化器，原始源过程的白度将传递到量化序列。因此，似然Pr{Hn|Z}就分解为每个对应符号对的概率的乘积。由于序列的独立同分布（Independent Identically Distributed，IID）性质，故两端的延伸符号集是独立的。

令Φ表示量化器输出过程的边际概率质量函数（Probability Mass Function，PMF），Q表示上述对应关系下的联合PMF，则有

且

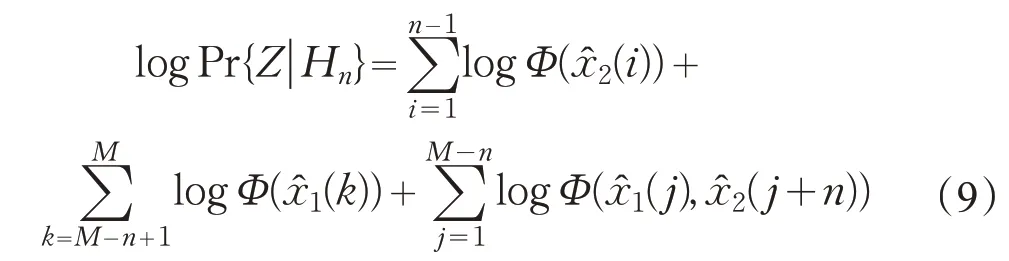
对于已知的噪声电平和量化器结构，Q（·，·）和F（·）可以预先计算并存储在检测器的查表中，然后，度量的计算包括在有限范围内进行简单的查找和数据求和，对于有限字母表的离散检测，这通常是可实现的，量化的相关性也可以用低复杂度的运算来实现。这将使得相对于非量化情形的总体复杂度降低，从而降低功耗并提高检测器的速度（这在检测器本身是传感器节点时可能很重要，如在集群层次结构中）。快速计算表明，式（6）和（9）对于每个成对的时延估计来说，需要大约DmaxM的查找加法。这些运算非常简单，可以连接到硬件中，以节省更多的功率。

2.2 量化

标准标量量化的目标是对用PDF描述的源数据以尽可能低的速率和最小平均失真进行编码，最常用的失真度量是平方误差

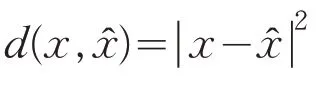
源分布失真的期望值

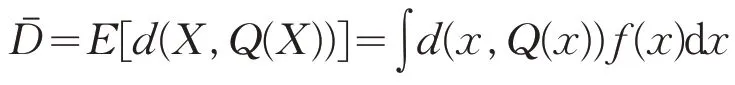
为量化数据与非量化数据之间的均方误差（Mean Squared Error，MSE）。这种失真度量的标准量化器设计算法是基于最近邻条件迭代地计算编码器分区，基于质心条件迭代地计算解码器重构级。然而，考虑到延迟估计任务和MAP检测算法，本文认为检测误差的概率是更合适的失真度量。

设Hn是真实假设，即n是两个序列之间的真实延迟，令为这个滞后时对应的符号对。我们知道，两个序列在任何滞后时的总的似然是在该滞后下对应对的似然的乘积。如果n是真实的滞后，则该符号对出现的概率就是。现在，采用MAP 检测方案，该符号对对滞后n（正确的滞后）的总对数似然和的贡献为，在任何其他滞后下的贡献是。对于低检测误差，我们希望最大化这些贡献之间的平均差，对于L-级量化器，这种差的期望值是对全部可能的符号对的平均

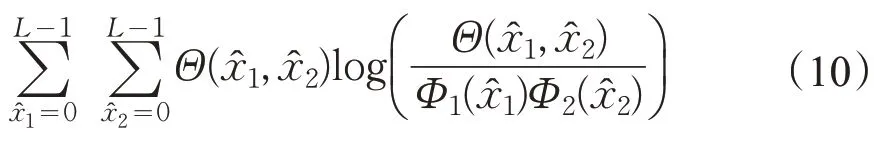
这个量是匹配和不匹配时联合分布的相对熵，或者是正确延迟下两个量化序列之间的交互信息。与“盲”设计相比，量化器设计在适当的延迟下最大化两个接收序列之间的交互信息，将会得到更低的延迟检测误差概率。我们称这种量化器为MaxMI（Maximizes the Mutual Information）量化器，该量化器设计只涉及到为量化器箱找到判决范围。如果采用对称的L-级量化，则每个输入值的量化仅需要L/2的比较加法。式（9）也可以解释为两个信号的似然度量值的相关性；由于MaxMI量化器对这些似然度量值进行了优化，所以有效地找到了量化信号的最佳再现级。

2.3 序列检测

2.1 节中的多假设检验框架可以直接应用于序列检测。检测过程如下，从传感器逐个采样接收量化数据，在每个假设下，将当前增强数据集的似然与阈值（基于期望误差概率计算的）进行比较，一旦其中一个似然超过阈值，相应的假设就被宣布为赢家，检测器发出信号，表示已经收到了足够的数据。对于固定的目标误差概率，判决所需的期望样本大小与全部假设对之间的最小分布距离成反比。由于MaxMI 量化器使得这个距离最大化，故它也是最优的序列检测器。

2.4 估计算法实现系统

将原始量化检测器设计（基于IID 高斯假设）直接应用于非平稳数据。首先将声学数据缩小到一个可处理的动态范围，并测量出经验均值和方差，进而用实测统计量将数据建模为IID 高斯，并在此模型基础上采用本文算法设计量化器和检测器。整个估计算法的实现过程如表1 所示，具体系统实现如图2 所示。

表1 MaxMI量化器和MAP检测器算法实现过程

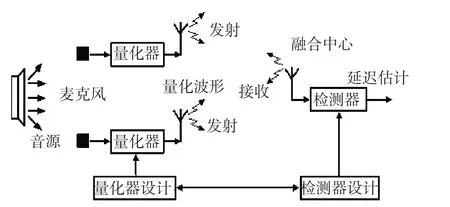
图2 延迟估计系统实现

3 实验结果及分析

3.1 实验设置

为了将本文的理论设计应用于实际源信号，我们对声学麦克风阵列数据进行实验。源数据在以下实验设置下获得；在一个长×宽×高=6 m×4 m×3.5 m室内房间里，录音和录制的噪音通过一个大的计算机扬声器播放，计算机为Lenovo/联想ThinkPad S2 201英特尔十代酷睿i7-8565U处理器笔记本电脑，并用一个8-元麦克风阵列捕捉这些声音，麦克风型号为TEVO-A2000 USB全向麦克风，可360o拾音，最大拾音距离可达4 m，USB接口连接，即插即用，能有效消除回音和背景噪音；录音由语音和音乐数据构成，采样频率为44.1 kHz，录制的噪音包括弥散和冲击噪音如高速公路的声音、雨、狗叫和背景中的人说话，通过笔记本电脑的扬声器播放。房间经过声学处理，混响时间约为300 ms，麦克风的放置高度大致相同，声源位于约2或3 m外，麦克风阵列配置如图3所示。声道1和声道3是活跃传感器。

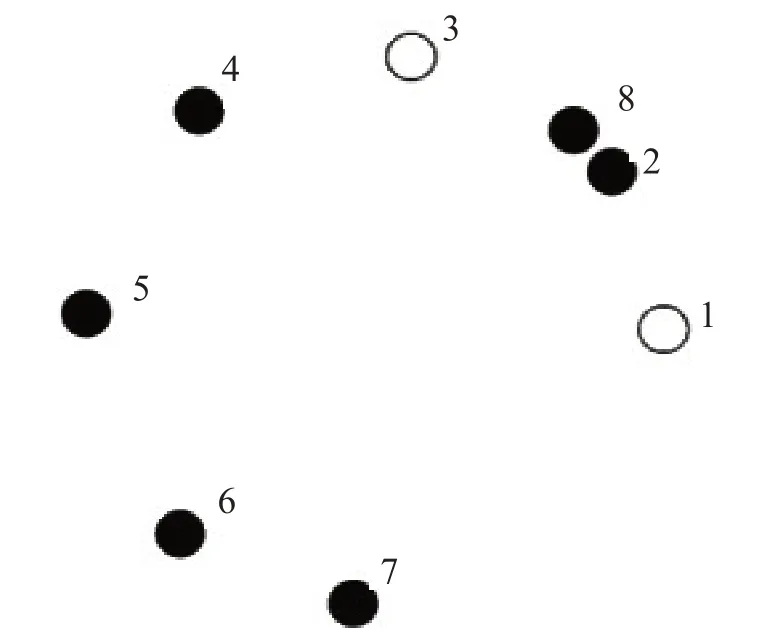
图3 麦克风阵列布置

3.2 实验结果

如图4 和图5 分别给出了在低信噪比（SNR=0 dB）和中等信噪比（SNR=6 dB）下语音和音乐数据的实验结果，图中显示的是来自活跃声道1和声道3的数据之间测量到的延迟与获得该估计值所需的时间（该时间是通过将检测块中的样本数量除以采样率得到）的关系。可以看到，采用本文算法设计的量化-检测器获得的延迟估计接近于非量化估计，并且在某些情况下优于非量化估计算法，即本文的Max-MI-MAP算法在同样的延迟时间里可以处理更多的样本数。还可看到，采用本文算法设计的量化-检测器获得的延迟估计明显优于基于MSE 的标准标量量化估计算法，这主要是由于后者采用的失真度量是量化数据与非量化数据之间的均方误差，而没有为其独特的统计数据建模。通过图4比较可以看到，对于语音数据，在低信噪比下，本文的MaxMI-MAP算法其平均延迟估计性能相比于非量化估计算法和基于MSE的标准标量量化估计算法，分别提高了大约8.5%和18.6%；在中等信噪比下，分别提高了大约10.3%和20.5%。通过图5 比较可以看到，对于音乐数据，在低信噪比下，本文的MaxMI-MAP算法其平均延迟估计性能相比于非量化估计算法和基于MSE的标准标量量化估计算法，分别提高了大约8%和18.2%；在中等信噪比下，分别提高了大约10.2%和20.4%。而对于如今大量存在的数据通信来说，更多的是数字信号的量化处理，所以本文的MaxMI量化器和MAP检测器算法能够更好地应用于实际场景。

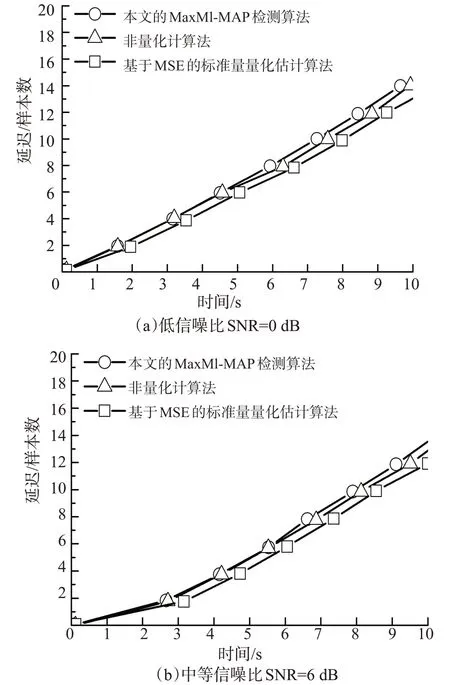
图4 不同量化-检测器在语音数据和3-级量化下的比较

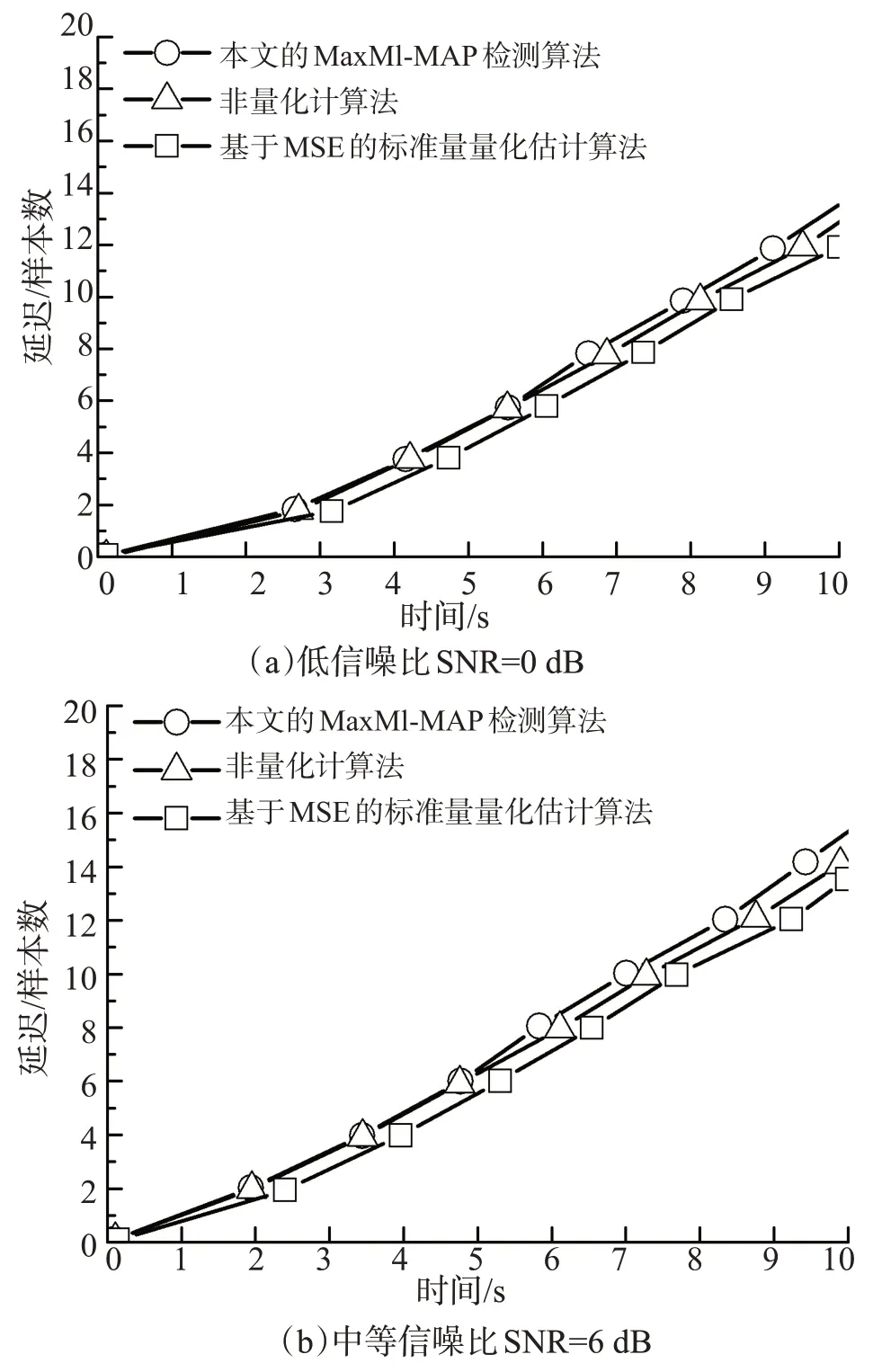
图5 不同量化-检测器在音乐数据和3-级量化下的比较

由于MaxMI量化检测器是专为不相关的高斯模型设计的，而在处理相关数据时，理想情况下，量化器将利用数据依赖关系，检测器在计算似然时将考虑这些依赖关系。为了对相关数据的这种依赖关系进行实验，我们在实验中设计了一种约束预测最大交互信息（Constrained-Prediction MaxMI，CP-MaxMI）量化器，其中每个数据样本的量化器输出依赖于前面样本的量化值。首先，给定一个量化级总数，然后，对输入波形逐个样本进行编码，使得与当前样本对应的量化箱被迫停留在前一个样本的几个量化箱内。例如，对于一个6-级（量化级总数为6）CP-MaxMI量化器，约束长度为3，当前输入或者采用与前面样本相同的箱进行编码，或者采用邻近的两个箱之一进行编码。

如图6 所示为采用CP-MaxMI 量化器在低信噪比（SNR=0 dB）和中等信噪比（SNR=6 dB）下应用于语音数据时和MaxMI-AP 量化器得到的比较结果。可以看到，CP-MaxMI 量化器的性能要优于原来的MaxMI-AP 量化器，特别是在较高的信噪比下。因为CP-MaxMI 量化器不但考虑了数据的依赖关系，而且通过给定量化级总数和约束长度，进一步提高了对似然的预测能力和处理精度，从而使得延迟检测更加准确。从图6 还可看到，同样的MaxMI-AP量化器，采用6-级量化时的性能要优于采用3-级量化时的性能，这是因为量化时采用的运算字长越长，量化误差就越小，故得到的性能就越好。

图6 可预测的MaxMI量化在语音和中低信噪比下的比较

4 结语

本文提出了一种应用于传感器网络数据延迟估计的联合量化-检测算法，给出了一个最大限度地实现接收信号之间的交互信息的非标准量化器以及一个假设检验检测器的设计。实验结果表明，本文提出的算法设计具有比标准MSE 量化器/相关检测器更好的性能。此外，与非量化相关技术相比，本文的量化检测器系统有更低的复杂度和更好的整体性能。

在今后的工作中，将研究不同传感器上不同级的非对称量化器，量化器速率（即发送的比特数）与检测性能之间的权衡也需要进行分析，也希望能对源和噪声分布建模不完善所造成的误差进行分析。定位问题的下一步自然是跟踪问题，还将探讨对多传感器和其他阵列处理问题的扩展。